飞行器套接螺栓定频振动疲劳失效分析

瞿绍奇，王武，邓进，郑宏海，邬亨贵

1.航空工业江西洪都航空工业集团有限责任公司，江西 南昌 330024

2.中国兵器工业209研究所，四川 成都 610041

飞行器在机载悬挂环境下要承受复杂的振动载荷。通常，飞行器作为机载悬挂物，在固定翼飞机挂载环境下，其振动环境工程上一般处理为由气动扰流诱发的宽带随机振动；在直升机挂载环境下，同时承受气动扰流诱发的宽带随机振动和由旋翼传递过来的定频振动环境[1]。飞行器结构在飞行过程中，经常出现经受振动环境作用，造成一些关键零部件产生疲劳破坏，导致发生飞行事故[2-5]。

振动疲劳的本质是结构受动态交变载荷的频率与结构固有频率重合或相近，使结构产生共振所导致的疲劳破坏现象[6]。目前，业内对随机振动疲劳损伤的计算研究较多[7-13]，其中，Dirlik 经验公式以其计算精度高、通用性强成为振动疲劳损伤估计的主流方法[14-17]；对结构正弦振动和定频振动的研究偏少[18-19]，其中，方红荣研究了气瓶在正弦振动环境下的损伤规律；薛立鹏推导了运载火箭在定频振动作用下结构疲劳损伤计算公式。而且，由于振动传递存在非线性，现有文献中对工程上非常普遍的机械连接结构振动失效的研究异常匮乏[20]。

本文针对某飞行器舱段套接螺栓在直升机定频振动环境下迅速断裂的现象，基于当前业内对结构振动疲劳失效主要由低阶固有频率共振造成的认知[21-23]，将飞行器结构简化为一阶弯曲固有频率处的单自由度系统，根据定频激励作用下结构响应的放大系数编制疲劳载荷谱，通过静力学分析获得螺栓头交变应力，结合Miner 线性累积损伤模型，对螺栓断裂现象进行了理论复现，并据此指导结构完成了优化改进设计。

1 定频振动疲劳分析理论

1.1 定频疲劳分析理论

根据疲劳寿命统计规律，疲劳寿命曲线幂指数[24]表达式为

式中:c，m为材料常数，N表示应力峰值为S时的破坏循环次数。根据Miner线性累积损伤理论[25]，多级应力下结构的累积损伤为

式中:ni为第i级载荷时的实际循环频次，Ni为第i级载荷时的破坏循环数，k为总载荷级数。

在某级定频载荷激励下，该级载荷的实际循环数与振动时间的关系为

式中:ωi为第i级定频振动的频率，Tw为振动时长。令D= 1，将式（1）、式（3）代入式（2），获得结构疲劳寿命估算公式

式中:Ts为结构的疲劳寿命。

1.2 定频振动放大系数

参考文献[19]～参考文献[21]研究成果，低频共振是飞行器结构振动失效的主要原因；据此，便于研究结构共振放大效应，将飞行器简化为一弯频率处的单自由度系统，其振动微分方程为

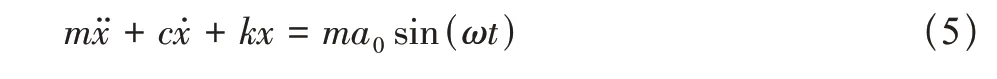
该方程的稳态解为

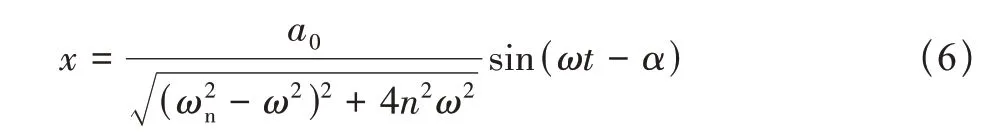
式中:n=c/2m，ωn为结构固有频率，ω为外加激励频率。对稳态解求二阶导，获得结构稳态加速度为

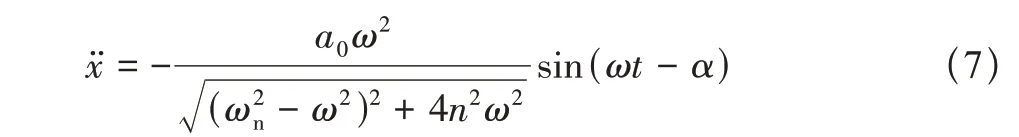
在加速度激励a0以频率ω作用下，结构加速度稳态响应的放大系数为

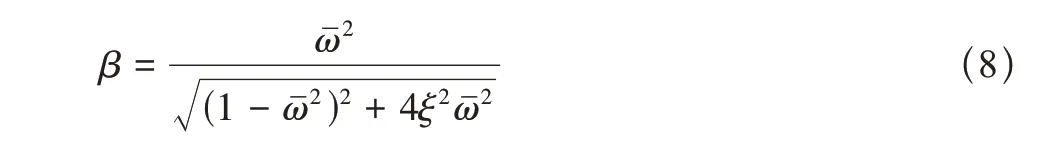
式中:ξ为结构阻尼比，ωˉ=ω/ωn。

2 飞行器套接螺栓载荷与应力

2.1 飞行器套接螺栓载荷分配

对飞行器舱段套接端面引入弯曲平面假设，则套接端面弯矩平衡方程为

式中:Fi为端面第i个螺栓剪力，R为舱段半径，αi为第i个螺栓占位角，p为螺栓总数量。

根据套接端面螺栓载荷与位移的线弹性关系，如图1所示，可建立端面螺栓载荷分配的线性关系

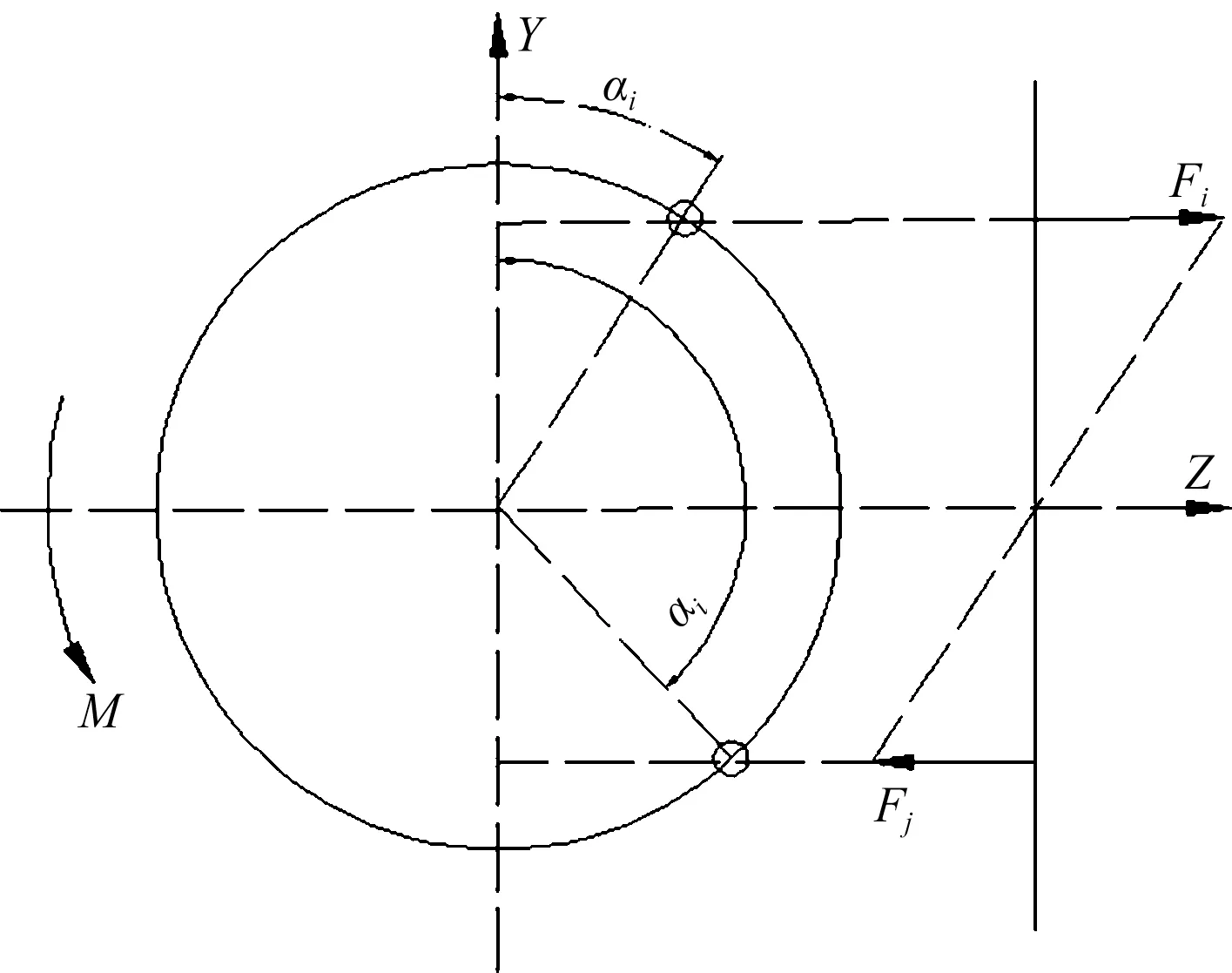
图1 套接端面承弯螺栓载荷分配关系Fig.1 Load distribution relationship to the bolt of countersunk section under bengding moment

将式（9）代入式（8），可获得套接螺栓载荷

2.2 套接沉头螺栓应力模型

工程上由于螺杆与螺孔间会预留装配间隙，套接沉头螺栓通过螺栓头传递剪力。如图2 所示，螺栓头在传递剪力Fx时，在其锥面上会产生附加载荷Fy；考虑螺栓头根部既是滑移止动区，又是刚度最强部位，因此，将载荷作用点设置在螺栓头根部；在附加载荷Fy作用下，该部位也是弯曲薄弱部位。

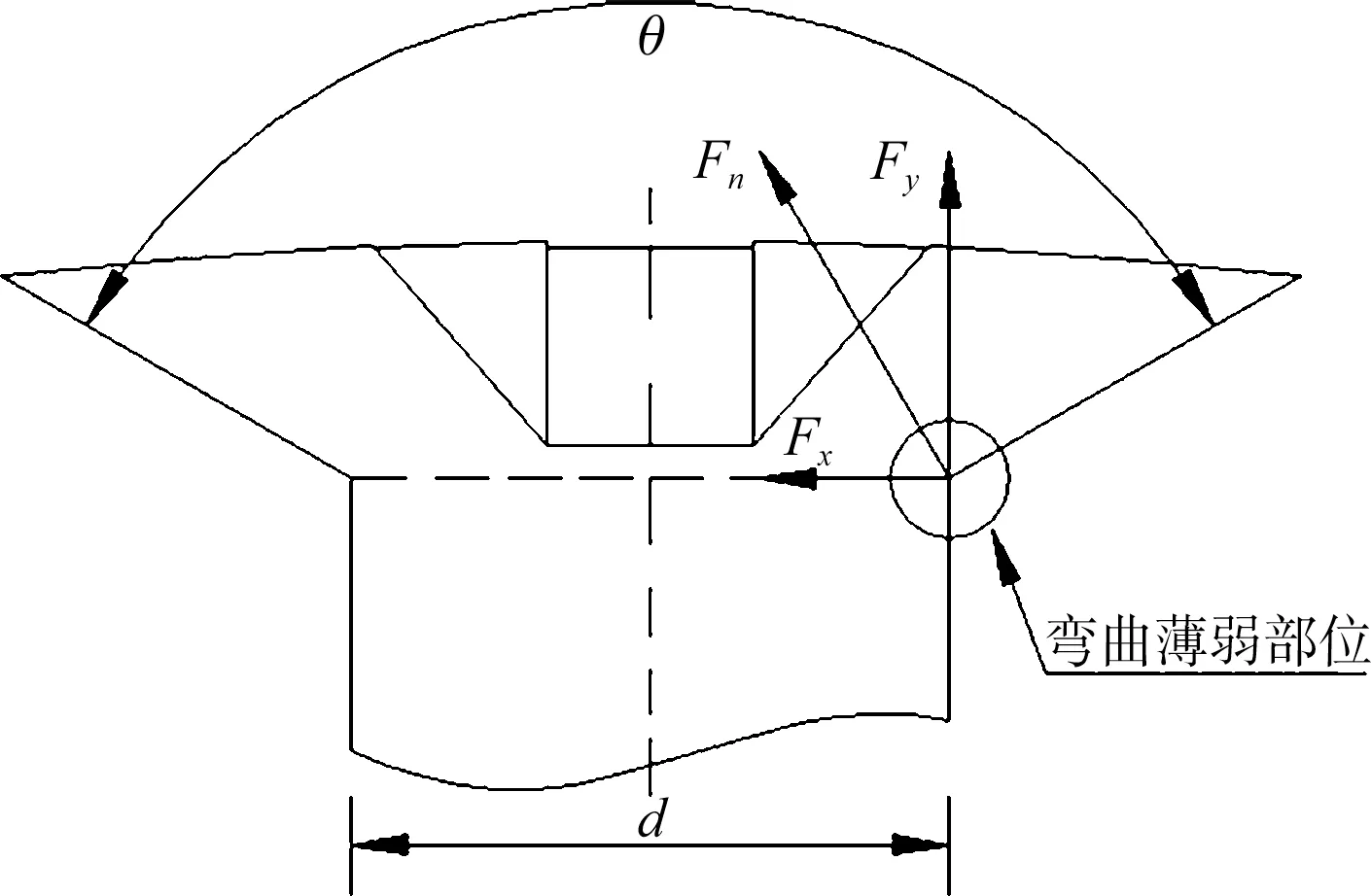
图2 套接沉头螺栓薄弱部位受力状态Fig.2 The load status of weak section of countersunk bolt

螺栓头根部截面弯矩

式中:d为螺栓直径，θ为螺栓沉头角。螺栓头根部弯曲应力

3 某飞行器定频振动疲劳分析

某飞行器悬挂于直升机短臂下，在开展耐久考核试验时，舱段套接螺栓发生了断裂，对该套接螺栓开展振动疲劳分析。

3.1 定频振动载荷谱编制

直升机挂载环境下，飞行器定频振动条件见表1。对飞行器悬挂状态开展有限元模态分析，获得结构一阶弯曲固有频率为97Hz；对图3 试验振动谱进行分析，飞行器在96Hz 定频处发生了共振现象；模态计算结果与试验现象一致。

表1 直升机定频振动条件Table 1 Dwell vibration condition of helicopter

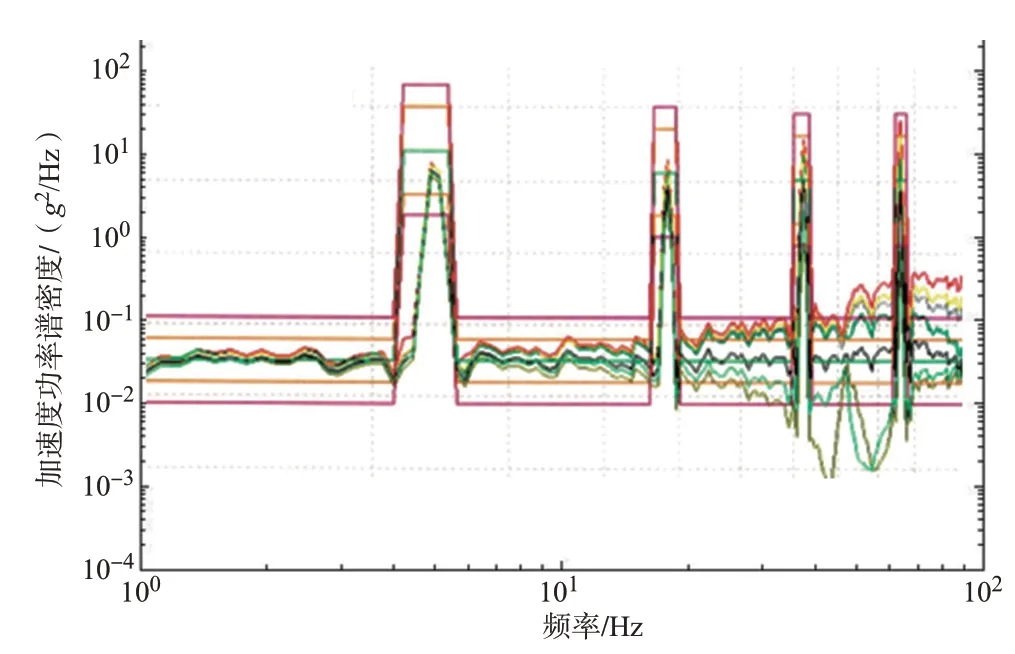
图3 飞行器振动试验监测振动谱Fig.3 Experimental monitor vibration spectrum of aircraft

取结构阻尼比ξ= 0.25，确定飞行器振动放大系数，设定试验时长T，编制疲劳分析载荷谱见表2。

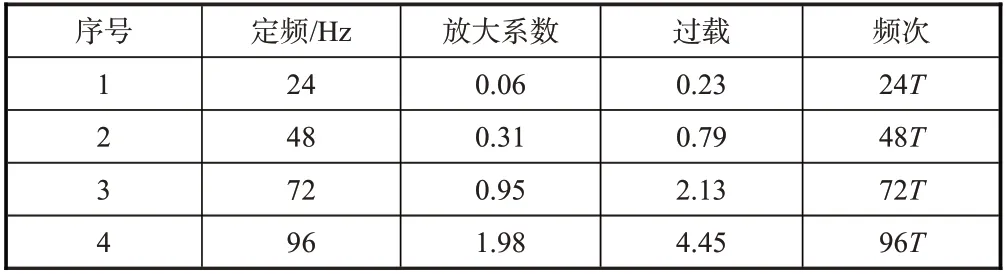
表2 飞行器振动放大系数和载荷谱Table 2 Load factor and load spectrum of aircraft

表2中计算获得的各定频处加速度响应放大系数变化趋势与图3所示试验监测情况一致，在96Hz定频处飞行器结构产生了显著的共振放大现象。

3.2 套接螺栓振动疲劳分析

断裂螺栓所在套接端面对称均匀布置12 个M5 螺栓，沉头角为120°；根据飞行器惯性载荷和支反力相对端面的距离，计算得到端面弯矩-过载系数为204.5N·m/g；据此，结合表2 所列经放大系数修正后各级载荷，分别根据式（11）和式（13），可获得各级载荷下断裂螺栓处交变载荷及交变应力见表3。

表3 断裂螺栓载荷与交变应力Table 3 Force and alternating stress of failure bolt

根据参考文献[26]所给30CrMnSiA不同应力集中系数材料S—N曲线，通过线性插值，获得应力集中系数Kt= 1时螺栓头处材料的S—N曲线数据见表4。

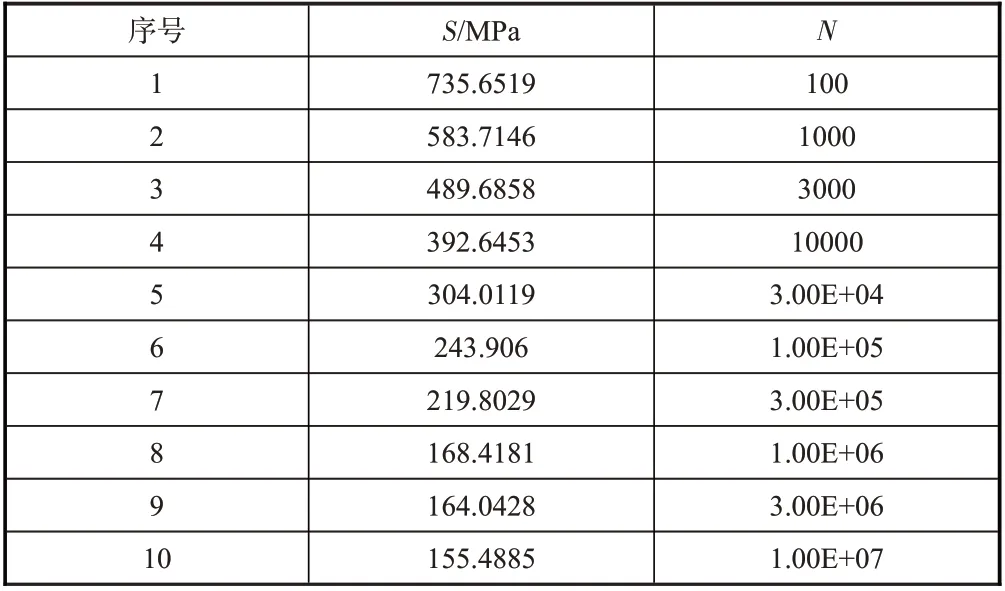
表4 螺栓头根部S—N曲线Table 4 S-N curve parameters of root part of countersunk bolt

飞行器稳定振动2min后，暂停试验对试验件状态进行检查，发现舱段套接螺栓头发生了断裂；以稳定振动时间作为疲劳分析输入，对飞行器断裂螺栓进行寿命评估。

表5 所列分析结果表明，飞行器在2min 定频振动载荷作用下，72Hz 和96Hz 交变载荷在螺栓头根部贡献了主要损伤，导致结构发生破坏，疲劳分析结果与试验现象符合；结合3.1节分析结论，结构破坏的原因为共振疲劳。

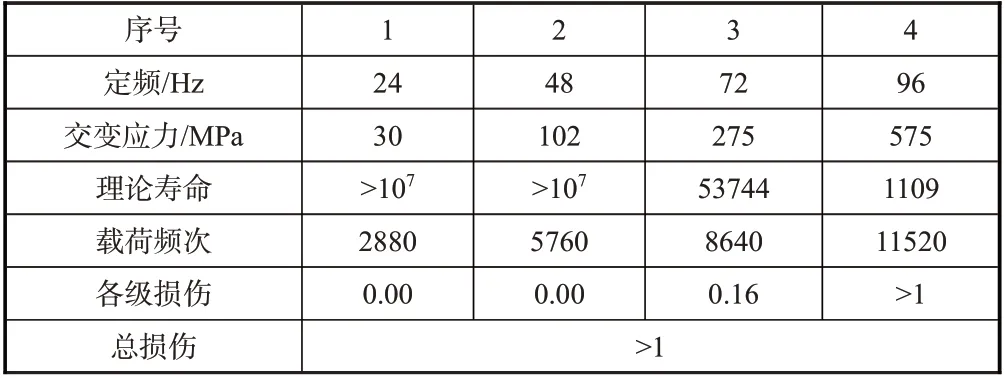
表5 断裂螺栓疲劳寿命评估Table 5 Fatigue life estimation of fracture bolt

3.3 结构改进分析验证

试验现象和疲劳分析结果反映:飞行器在96Hz定频处产生了共振，显著放大振动量级；螺栓在96Hz 定频振动处累积损伤大于1，疲劳裕度不足。

基于上述分析，对飞行器结构开展长寿命优化设计:对质量分布特性进行调整，将结构一阶弯曲频率优化为154Hz；将舱段套接螺栓优化为M6的90°沉头螺栓。

优化后原断裂螺栓端面弯矩-过载系数为120N·m/g。对原断裂部位螺栓开展定频振动疲劳分析见表6，各级定频载荷未对结构振动产生放大效应，对应的交变应力均低于材料疲劳极限，循环次数超过了107次，螺栓寿命达到了100min的使用需求。

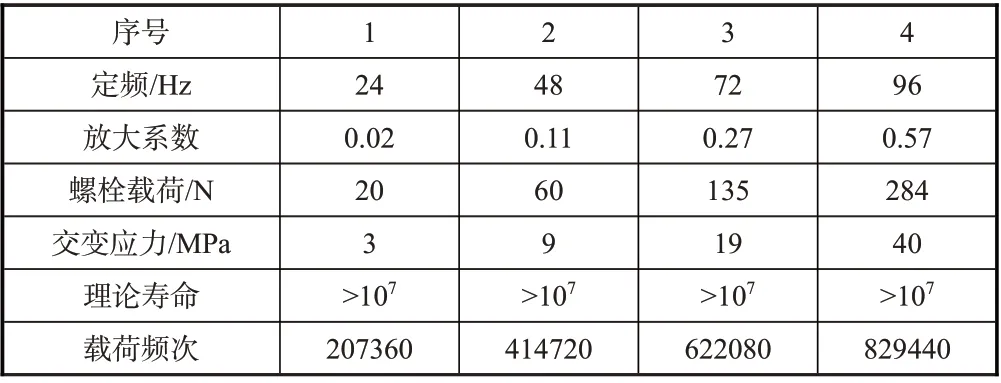
表6 优化后原断裂部位螺栓疲劳寿命评估Table 6 Fatigue life estimation of fracture bolt after optimization

对优化后飞行器结构开展耐久振动试验验证，飞行器振动试验结构两处监测点振动功率谱如图4所示，对比图3可发现飞行器结构未产生共振现象；振动100min后对试验件状态进行检查，套接螺栓未发生破坏。

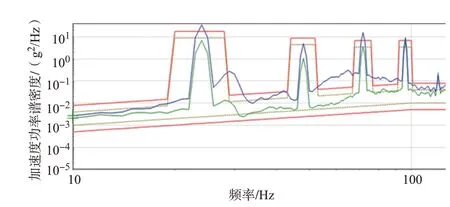
图4 优化后飞行器振动试验监测振动谱Fig.4 Experimental monitor vibration spectrum of aircraft after optimization

表6 所列分析结果在定频振动放大趋势上与图4 试验现象一致，寿命分析结果与试验结果吻合；并再次验证了所提定频振动疲劳分析方法在飞行器连接结构寿命评估中的工程指导作用。

4 结论

通过研究，可以得出以下结论:

（1）将飞行器结构简化为一阶弯曲频率处的单自由度系统，在定频振动作用下，获得的结构响应放大趋势与试验监测趋势一致。

（2）采用单自由度系统激振放大系数修正和定频振动频次编制疲劳载荷谱，基于静力学分析获得交变应力，结合Miner线性累积损伤模型，构建的套接螺栓定频振动疲劳寿命评估方法，其分析结果与试验结果吻合。