异步感应线圈推进器推力稳定性研究

2022-07-01马偃亳于德江李振超赵婉瑜

电工电能新技术 2022年6期

马偃亳，于德江，陈帅，陈东，李振超，赵婉瑜

(中国电子科技集团公司第二十七研究所，河南郑州 450047)

1 引言

同轴感应线圈推进器(Coaxial Induction Coil ElectroMagnetic Launcher，CICEML)分为同步感应线圈推进器(Synchronous Induction Coil ElectroMagnetic Launcher，SICEML)和异步感应线圈推进器(Asynchronous Induction Coil ElectroMagnetic Launcher，AICEML)[1]。同步线圈推进器，采用序列脉冲电源依次触发放电，驱动电枢不断加速前进[2,3];而异步线圈推进器，采用多相绕组配合多相交流脉冲电源，通过控制交流脉冲电源的放电相序，在轴向推进器里产生交变的磁动势，驱动电枢加速前进[4]。目前，同步线圈推进器的研究居多。同步线圈推进器具有较高的推射效率，但是需要精确的位置检测装置来触发相应位置的脉冲电源，控制复杂；同时，同步线圈推进器对电枢作用力集中在尾部，会造成电枢尾部应力集中、温升过高等问题。异步线圈推进器不需要精确的位置检测装置，且感应涡流、电磁应力和温升分布在电枢的整个身长上，使电枢具有磁悬浮和自动对中的特性，提高了推进器的稳定性[5]。当前对同轴线圈推进器的研究大多集中在推射效率和推射速度的提高[6,7]，而不关注推射过程推力的波动情况及稳定性。当同轴线圈推进器只用来加速电枢时，电枢的出膛速度和推射效率越高越好，然而当电枢前后带有助推载荷时，除了关注载荷的出膛速度和推进器的推射效率，还要关注载荷的推力稳定性、磁场抗性和过载抗性等问题，例如加速助推无人机和制导弹药[8]、无人机的飞控系统、导弹的引信等，通常含有电气元件、精细结构件或磁敏感元件，在不稳定推力、强冲击、强磁场作用下，结构容易变形，电气元件容易失效，从而影响载荷的助推起飞。本文通过Ansoft maxwell仿真软件建立仿真程序，分别从电枢初始位置、相间间隔[9]、电枢长度、电枢厚度4个维度对单段三相异步线圈推进器进行仿真分析，探索异步线圈推进器推力稳定性和载荷出口速度影响关系，为后续推射载荷稳定发射试验提供依据和指导。

2 异步感应线圈推进器原理及数理模型

2.1 工作原理

异步感应线圈推进器的工作原理和直线感应电机的工作原理类似。同轴排列的初级线圈通过串联或并联连接构成多相绕组，多相绕组由多相交流脉冲电源激励，产生一个类似异步电机旋转磁场的直线行波磁场，行波磁场速度始终快于电枢速度，借助两者之间的速度差驱动电枢加速前进[10]。本文中单段异步线圈推进器采用驱动线圈反串联结构，电源采用三相交流脉冲电容器，系统模型如图1所示。

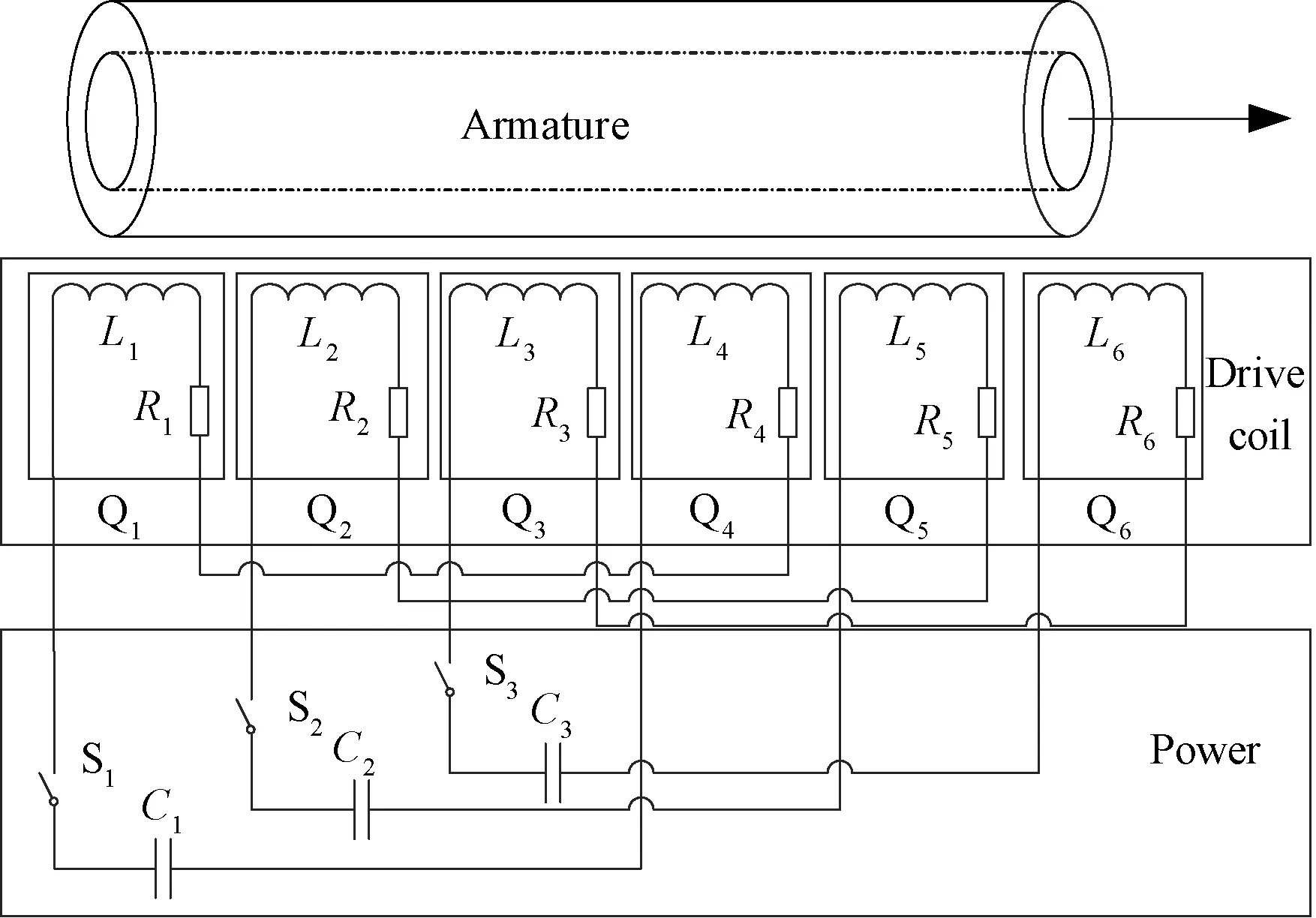
图1 三相异步感应线圈推进器系统模型Fig.1 System model of 3-phase asynchronous induction coil electromagnetic launcher

单段推进器由6个驱动线圈构成，从尾部到头部依次编号为Q1、Q2、Q3、Q4、Q5、Q6，6个驱动线圈缠绕方向相同。以A相为例，A相脉冲电容器C1的正极通过开关器件S1与线圈Q1进线端连接，Q1的出线端和Q4的出线端反向串接，Q4的进线端再连接到A相脉冲电容器的负极构成A相回路。同理，C2、S2、Q2构成B相，C3、S3、Q3构成C相，各相电回路独立连接，工作时，通过电磁场耦合关系影响各相电参数。

2.2 推力数理模型

同轴线圈推进器工作时，电枢上感应电流呈环状分布，因此，在搭建数理模型时，通常将电枢看作许多相互绝缘的电流环[11]。这些电流环可以看作是多个相互独立的线圈，单个独立的线圈在电路模型中就可以等效为电感和电阻的串联回路。当驱动线圈中通入外部电流时，在电枢的电流环上会感应出电流,这个感应电流在驱动线圈磁场的作用下会在径向和轴向上产生电磁力，其中径向上的力在整个圆环上相互抵消，对电枢整体运动无影响，而轴向上的电磁力，方向唯一，驱动电枢加速运动。同轴线圈推进器电流环模型如图2所示。图2中，iD为驱动线圈分片电流，iP为电枢分片电流，R为驱动线圈分片半径，r为电枢分片半径，z为驱动线圈分片和电枢分片距离。

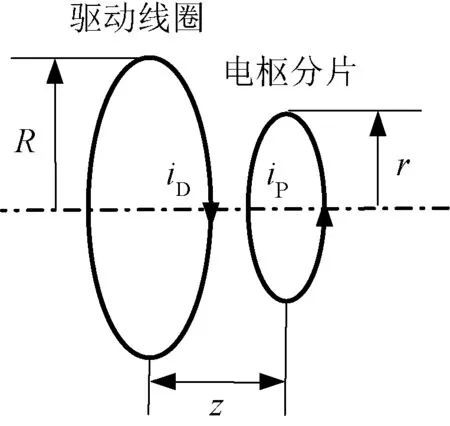
图2 电流环模型Fig.2 Model of current loop

本文研究的推力稳定性只和电枢轴向受力有关，采用电流丝法[12]求解得到电枢轴向受力如下：

(1)

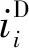
2.3 单段三相异步感应线圈设计参数

本文所设计三相异步感应线圈用于3.5 kg折翼式无人机的发射，全系统设计参数见文献[13]。无人机加速起飞过程中，既要考虑无人机内部器件磁场抗性和过载抗性，同时又要考虑推力的稳定性。本文只研究单段推进器推力稳定性和载荷出口速度影响因素，不再对其他发射要素进行研究。单段推进器设计参数见表1，实物图如图3所示。

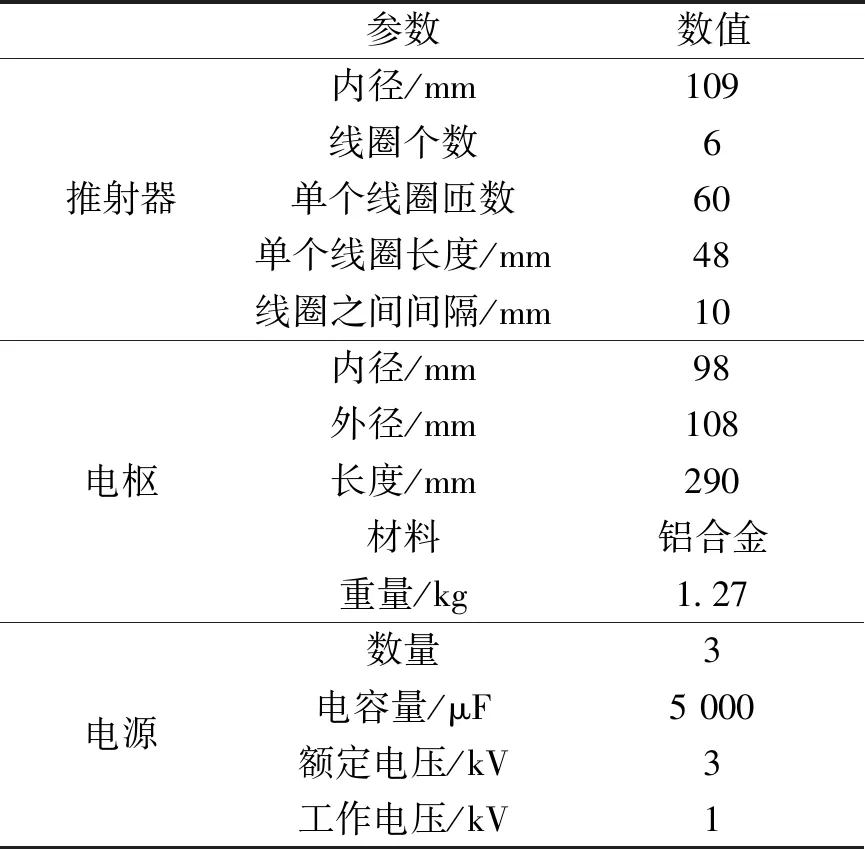
表1 系统参数Tab.1 System parameters

图3 单段三相异步感应线圈推进器Fig.3 Single-section 3-phase asynchronous induction coil electromagnetic launcher

单段推进器由6个线圈组成，每个线圈匝数为60匝，推射器内径109 mm，推射器骨架壁厚3 mm，单个线圈长度48 mm，线圈之间间距10 mm，线圈采用1.2 mm×10 mm紫铜带四饼缠绕，单个线圈厚22.5 mm。

推射载荷由电枢、尼龙连接块和模拟载荷三部分构成，如图4所示。电枢内径98 mm，外径108 mm，模拟载荷通过尼龙连接块和电枢相连，工作过程中，电枢通过尼龙连接块带动前端模拟载荷共同运动，从而达到加速模拟载荷的目的，电枢重量1.27 kg，连接块重量0.57 kg，模拟载荷重量3.5 kg。

图4 推射载荷组成Fig.4 Constitution of ejection load

电源采用能够正反向充放电的交流脉冲电容器，反充比接近1，电源额定电压3 kV，实际工作电压1 kV，电源额定电容量5 mF，三相线圈分别和三个交流脉冲电源连接，构成三个独立的LCR振荡回路。

本文基于上述单段三相异步感应线圈推射器的参数，在Ansoft maxwell 中建立推射器有限元仿真模型如图5所示，通过改变电枢初始位置、相间间隔、电枢长度、电枢厚度等参数，研究推进过程中对载荷出口速度和电枢受力稳定性的影响关系。

图5 有限元仿真模型Fig.5 Finite element simulation model

3 异步感应线圈推进器推力稳定性分析

异步感应线圈推进器推力曲线呈双驼峰分布，推力大小与多相电源电流大小、电流变化率、推进器内磁动势合成以及电枢速度大小相关。以三相异步感应线圈推进器为例，A、B、C三相电源依次放电，电枢受到随时间变化的推力曲线，推力曲线波动频率与三相电流频率相关，而电流频率与系统电参数相关，如图6所示。实际加速过程中，从第三个峰值推力开始，由于电路损耗、电流衰减以及电枢运动造成驱动线圈和电枢之间的耦合作用大大降低，推力峰值远远小于前2个推力峰值，对电枢的推进效果非常小，基本可以忽略，故本文只研究前两个峰值推力的影响因素。

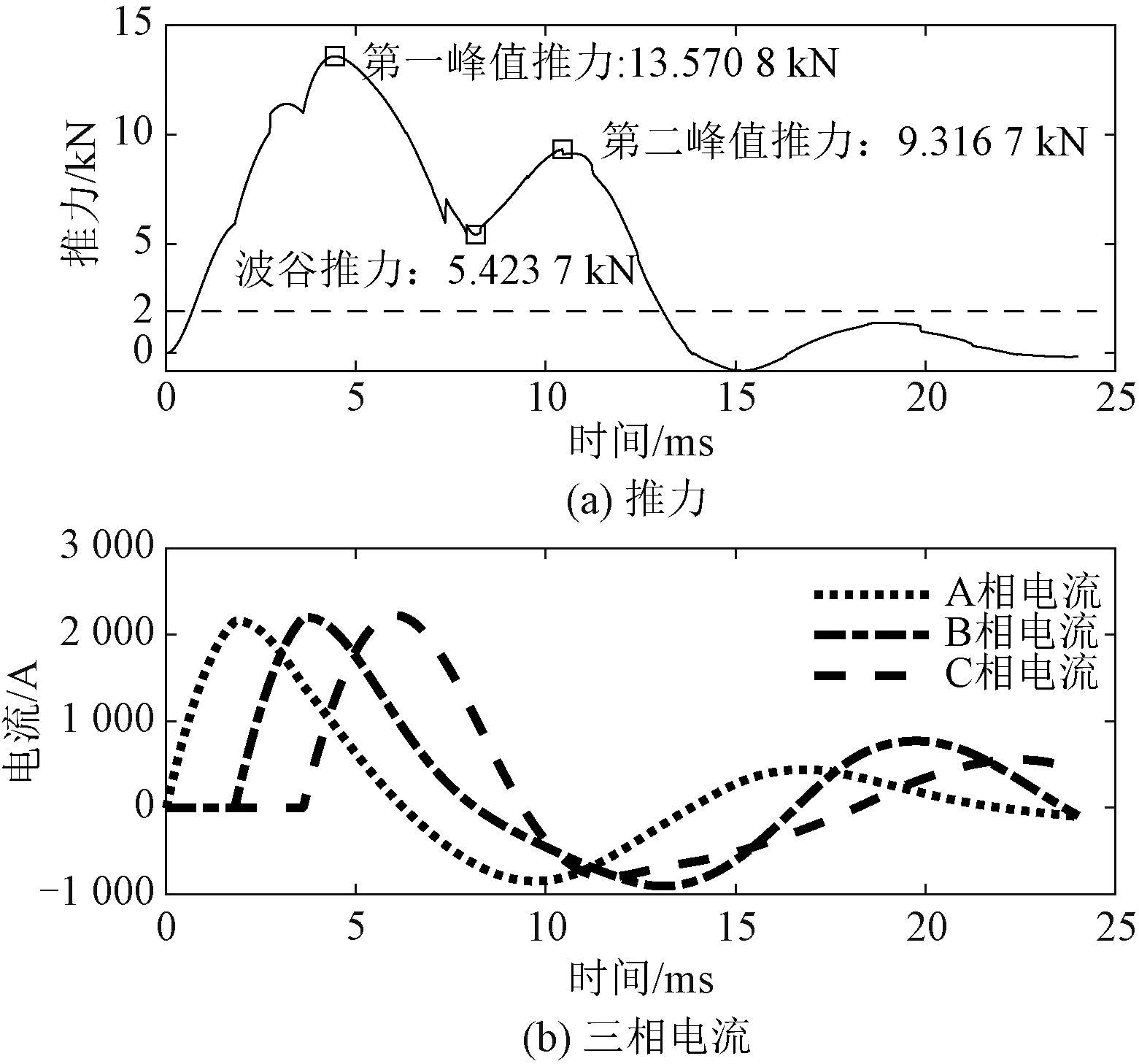
图6 双驼峰推力曲线及三相电流曲线Fig.6 Double-hump force curve and 3-phase current curves

通常采用标准差来衡量曲线的波动性。本文通过计算大于2 kN下载荷所受推力的标准差大小来评估推力的稳定性，标准差越小，则推力越稳定，反之则稳定性越差。推力标准差计算公式如下：

(2)

3.1 电枢初始位置对推力稳定性影响

电枢初始位置定义为电枢尾部到第一个线圈尾部的距离[14]，如图7所示。

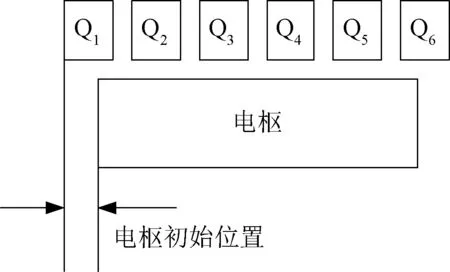
图7 电枢初始位置定义Fig.7 Definition of armature initial position

为研究电枢初始位置0～60 mm对推力波动性影响，电枢初始位置分别在12 mm、24 mm、36 mm、48 mm下的推力曲线如图8所示。

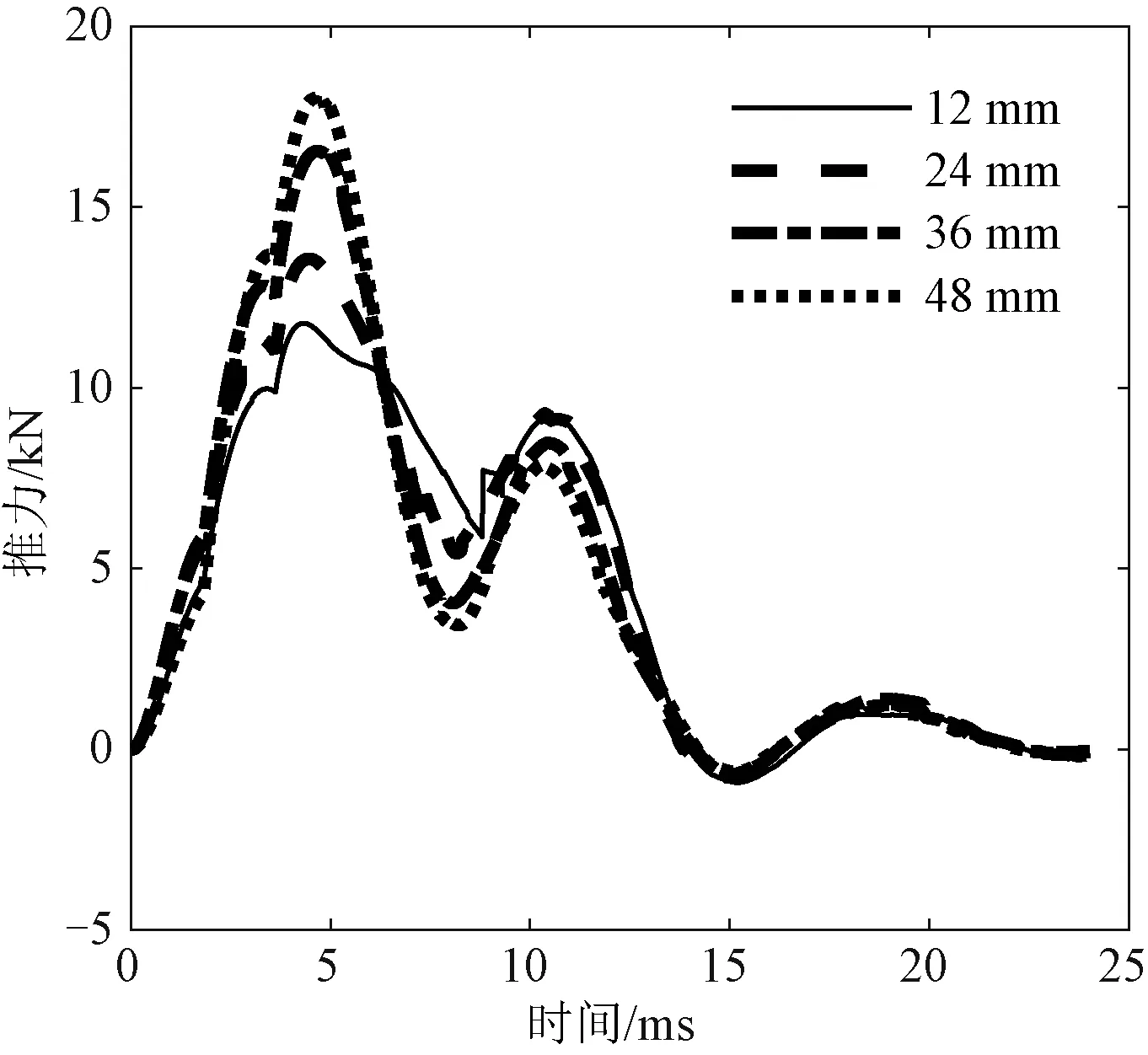
图8 电枢不同初始位置下推力曲线Fig.8 Force curves of armature at different initial positions

将电枢初始位置0～60 mm下推力曲线的双驼峰峰值大小及发生时刻、波谷值大小及发生时刻、出口速度统计见表2。

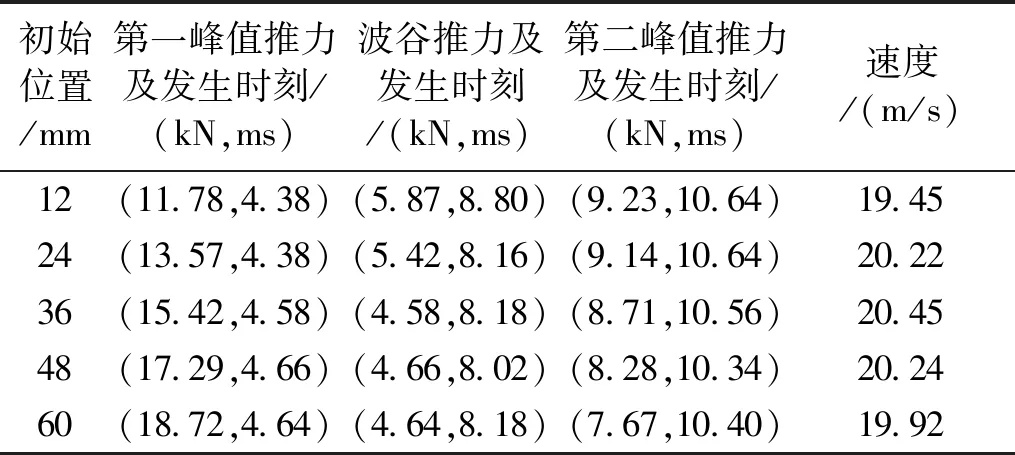
表2 电枢初始位置对推力特性和出口速度的影响Tab.2 Influence of armature initial positions on force characteristics and muzzle velocity

如图8和表2所示，随着电枢初始位置的增加，第一个峰值推力增加，波谷推力减小，第二个峰值推力减小，从而造成第一个峰值与第二个峰值之间的差值增加，推力波动性增大，不利于实现推射载荷的稳定发射。上述5种初始位置对比，12 mm下两个峰值推力和波谷推力更加平滑，更利于实现载荷的稳定发射。

由表2可知，第一个推力峰值大概在4.5 ms左右产生，4.5 ms时电枢初始位置在12 mm和48 mm下驱动线圈和电枢电流密度分布如图9所示。

图9 4.5 ms时驱动线圈与电枢电流密度分布图Fig.9 Current density distribution of drive coils and armature at 4.5 ms

如图9所示，4.5 ms时，电枢初速位置48 mm下电枢上感应电流密度分布范围和大小大于电枢初始位置12 mm。4.5 ms时，A、B、C三相电源均已触发放电，此时A相电流已由最大值衰减至不足峰值一半大小，而B相电流在峰值附近，C相电流正在急速增加，此时B、C相线圈电流对电枢的加速起主导作用。电枢初始位置在12 mm处时，由于初始位置靠近推进器尾部，4.5 ms时，电枢运动距离较短，电枢头部尚未完全进入C相线圈作用范围，降低了驱动线圈和电枢的耦合长度。而电枢初始位置在48 mm处时，运行到4.5 ms时，电枢正好完全进入B相和C相线圈作用范围，耦合作用强，推力大。

采用相同方法分析第二个峰值时刻时初始位置12 mm和48 mm下推力特性，如图10所示，第二个峰值时刻大约在10.5 ms。

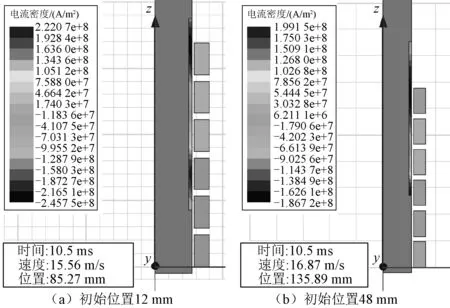
图10 10.5 ms时驱动线圈与电枢电流密度分布图Fig.10 Current density distribution of drive coils and armature at 10.5 ms

10.5 ms时，电枢初始位置12 mm下电枢电流密度范围和大小均大于48 mm，耦合长度长，故初始位置12 mm下耦合作用强，推力也较大。同样，波谷推力在不同初始位置下的变化因素也与驱动线圈和电枢的耦合作用有关，此处不再展开分析。

图11通过绘制不同电枢初始位置下载荷出口速度曲线和大于2 kN推力的标准差曲线来分析电枢初始位置对推射载荷出口速度和推力稳定性的影响关系。

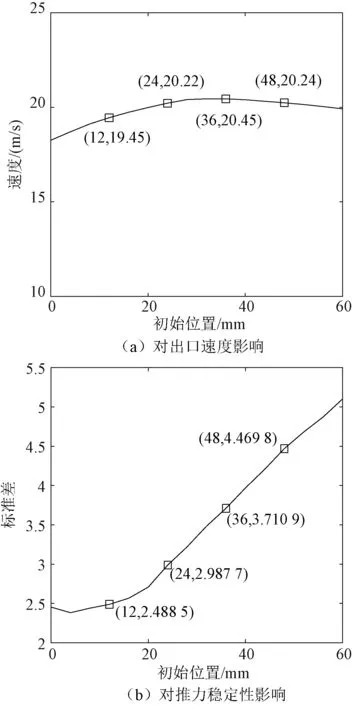
图11 电枢初始位置对出口速度和推力稳定性影响Fig.11 Influence of armature initial positions on force stability and muzzle velocity

随着电枢初始位置的增加，载荷出口速度先增大后减小，电枢初始位置在32～36 mm之间，载荷出口速度有最大值，约20.45 m/s；随着电枢初始位置的增加，推力曲线标准差不断增大，推力波动性逐渐变得剧烈，稳定性变差，当电枢初始位置在4 mm处，大于2 kN下推力的标准差最小，推力最稳定。

在实际发射载荷时，不会选择大于36 mm的电枢初始位置，因为此时载荷出口速度和推力稳定性都不是最优；当选择32～36 mm的电枢初始位置时，此时载荷有最大出口速度，但是要评估载荷的过载抗性和受力波动性影响，如果载荷内部有器件结构损坏或元器件失效，就可以通过减小电枢初始位置的方法来降低最大推力、提高推力稳定性。

3.2 相间间隔对推力稳定性影响

保持电枢初始位置24 mm不变，相间间隔选取1.0～3.6 ms，其他参数不变，图12为相间间隔1.4 ms、1.8 ms、2.2 ms、2.6 ms下的推力曲线。

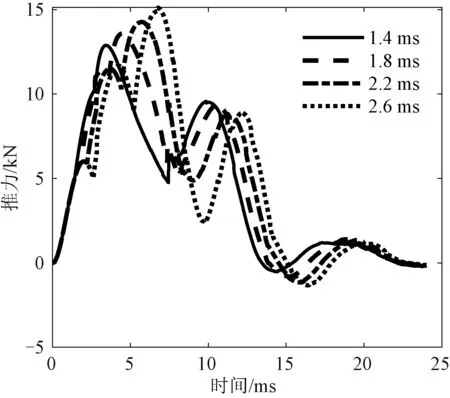
图12 不同相间间隔下推力曲线Fig.12 Force curves of different phase intervals

表3对相间间隔选取1.0～3.0 ms下推力曲线的双驼峰峰值大小及发生时刻、波谷值大小及发生时刻、出口速度进行统计。

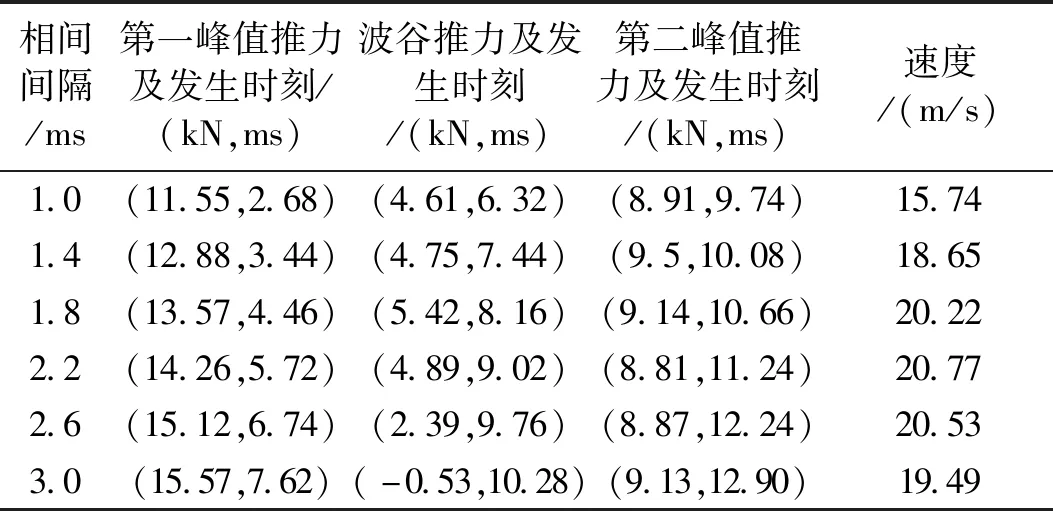
表3 相间间隔对推力特性和出口速度的影响Tab.3 Influence of phase intervals on force characteristics and muzzle velocity

随着相间间隔增大，第一峰值推力不断增大，波谷推力先增大后减小，在相间间隔为1.8 ms时，波谷推力最大,在相间间隔超过3.0 ms时，波谷推力甚至降到了0 kN以下，此时推力波动剧烈，稳定性极差；第二峰值推力随着相间间隔改变变化不大；随着相间间隔增大，所有峰值时刻和波谷时刻均延后，整个双驼峰推力持续时间增加。

由于相间间隔超过3.0 ms时，波谷推力会降到0 kN以下，而本文衡量推力稳定性的作用力范围是在双驼峰推力持续期间大于2 kN推力的标准差，当低于2 kN时，可以从推力曲线中直观观测到推力波动性剧烈如图13所示。

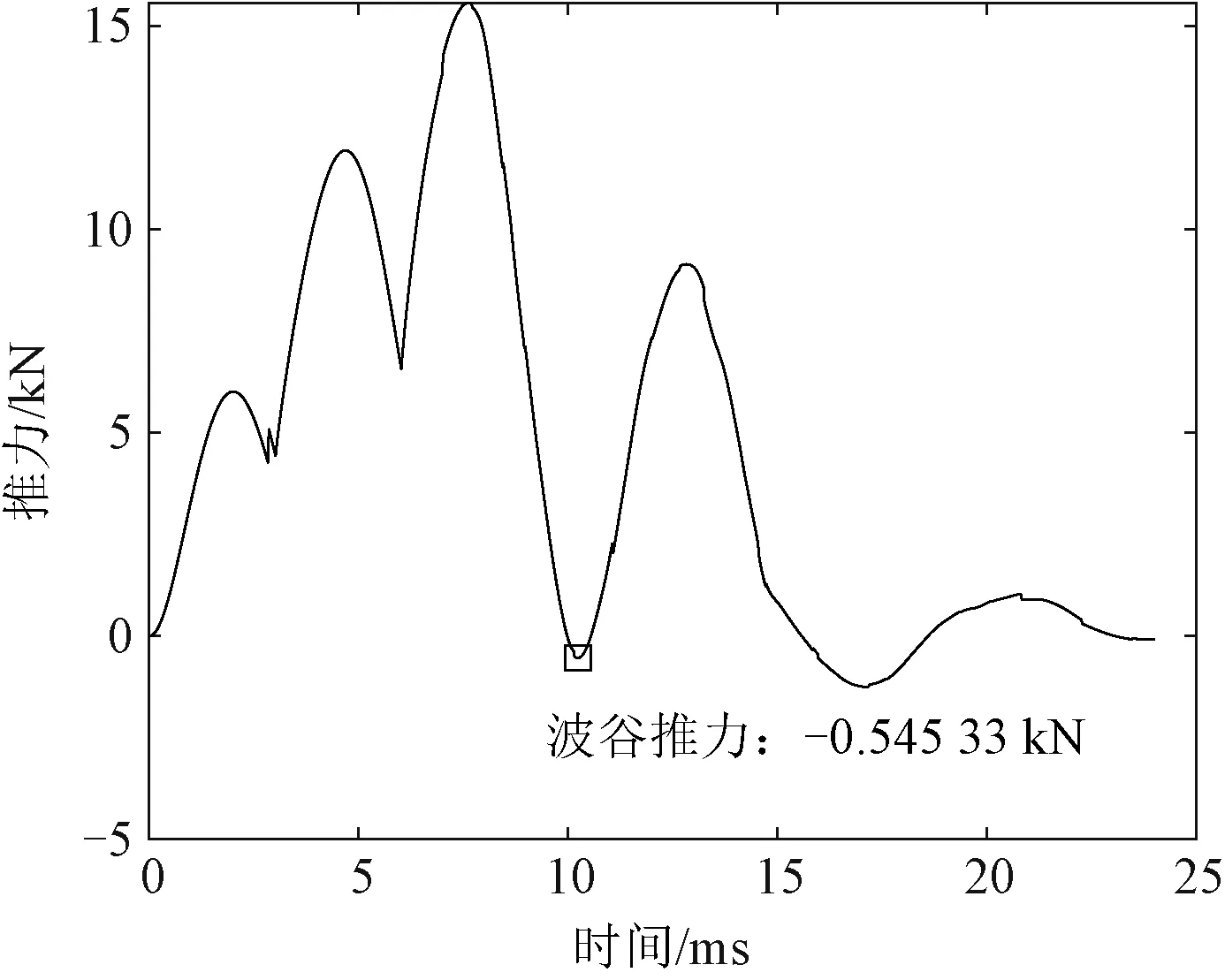
图13 相间间隔3.0 ms时的推力曲线Fig.13 Force curve at trigger time interval of 3.0 ms

图14分析1.0～2.6 ms相间间隔对载荷出口速度和推力稳定性的影响关系。

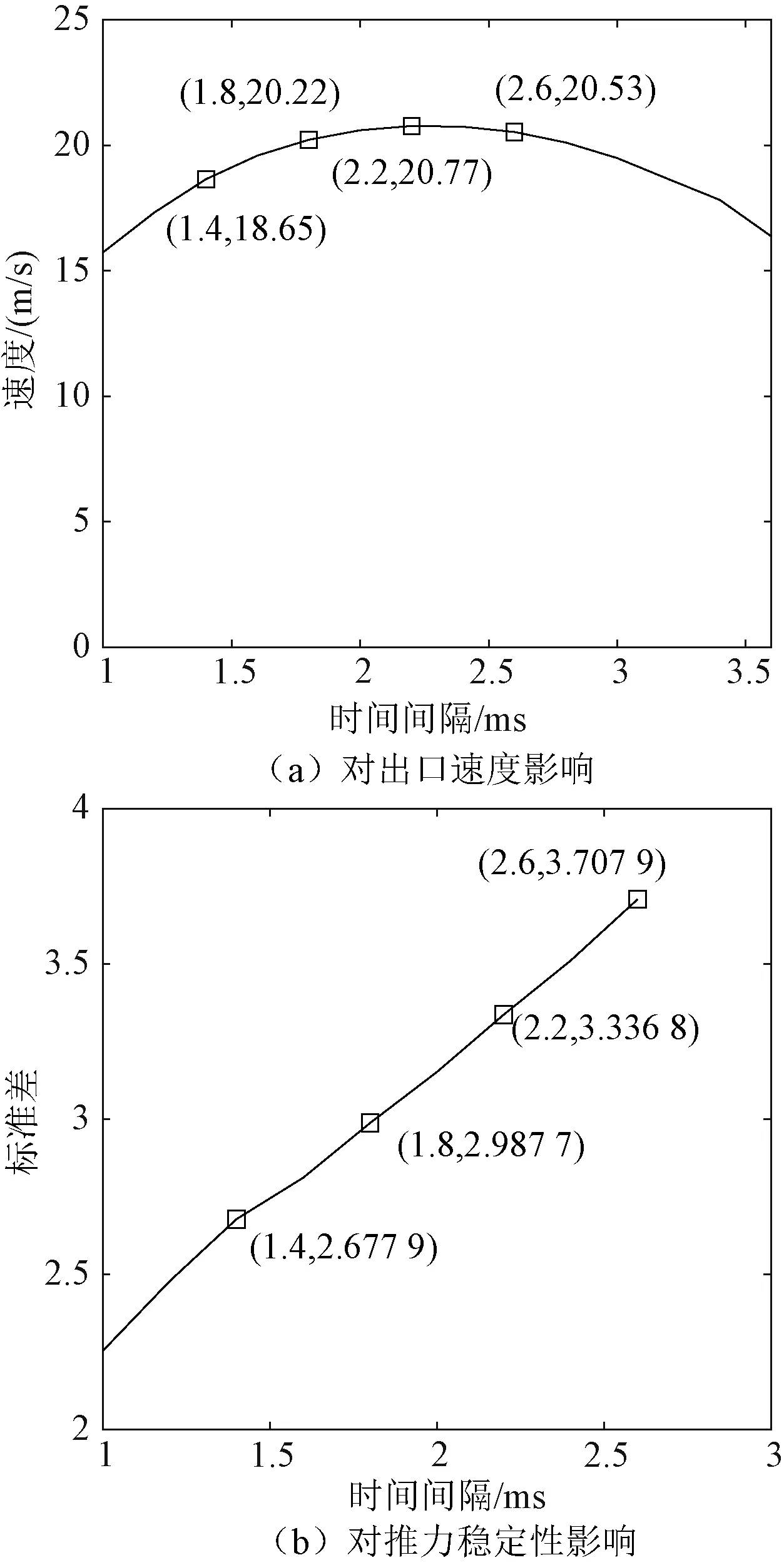
图14 相间间隔对出口速度和推力稳定性影响Fig.14 Influence of phase intervals on force stability and muzzle velocity

随着相间间隔增加，载荷出口速度先增大后减小，在相间间隔2.2 ms下达到最大20.77 m/s；由推力标准差曲线图可知，随着相间间隔的增大，推力稳定性越来越差。

同电枢初始位置分析一样，在实际推射载荷时，不可能选择大于2.2 ms的相间间隔，因为此时载荷出口速度和推力稳定性都不是最优，同样，要根据载荷的速度指标要求、过载抗性和受力波动性影响来选择最优相间间隔。

3.3 电枢长度对推力稳定性影响

改变电枢长度，在不改变电枢厚度的情况下，电枢重量会改变，从而影响整个推射载荷重量。本项研究通过改变连接结构和模拟载荷重量来保持整个推射载荷重量不变，电枢长度取250～350 mm，电枢初始位置24 mm，相间间隔1.8 ms。图15为电枢长度分别为270 mm、290 mm、310 mm、330 mm下的推力曲线。

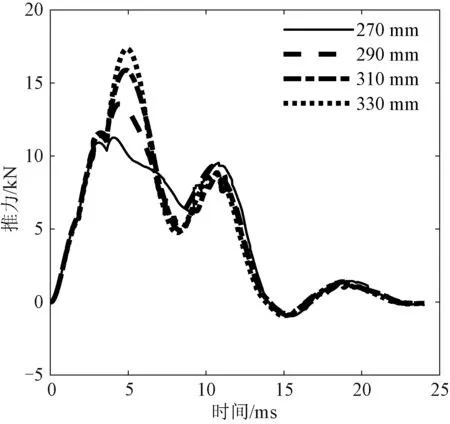
图15 不同电枢长度下推力曲线Fig.15 Force curves of different armature lengths

表4对不同电枢长度下推力曲线的双驼峰峰值大小及发生时刻、波谷值大小及发生时刻、出口速度进行统计。

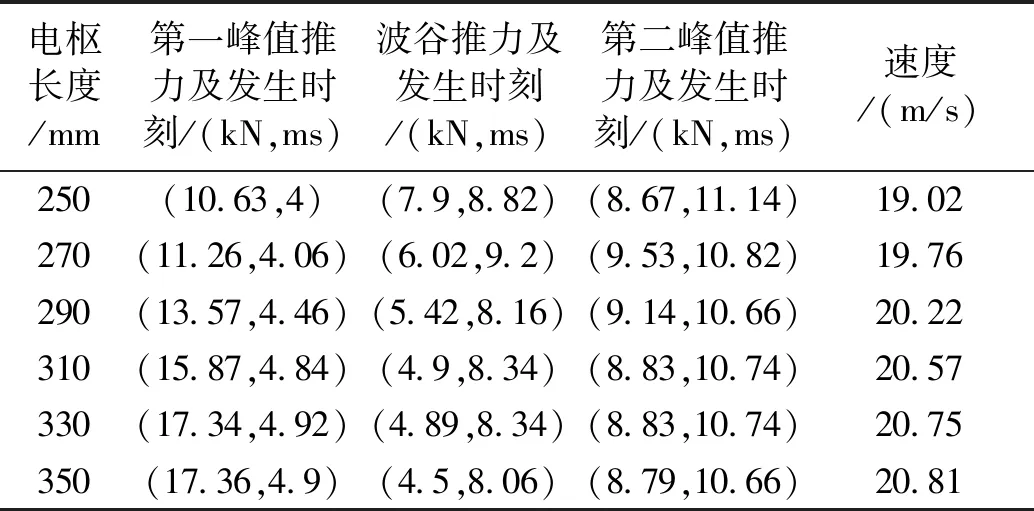
表4 不同电枢长度对推力特性和出口速度的影响Tab.4 Influence of different armature lengths on force characteristics and muzzle velocity

随着电枢长度增加，第一峰值推力明显增加，波谷推力稍有减小，第二峰值推力基本不变；随着电枢长度增加，第一峰值推力发生时刻稍有延后，波谷推力和第二峰值推力发生时刻稍有提前，发生时刻总体变化不大。

电枢长度增加，最明显的变化就是第一峰值推力增加，这由前面的长度耦合理论很容易分析，电枢长度增加后，就会增加驱动线圈和电枢的耦合长度，从而使推力增加；而波谷推力和第二峰值推力变化不明显，这是由于在保持整个推射载荷重量不变的前提下，电枢运动到推力波谷和第二峰值时，电枢头部均已运动出最末端驱动线圈，此时电枢与驱动线圈的耦合长度基本一致，故受力情况也变化不大。

图16为电枢长度对载荷出口速度和推力稳定性的影响关系。

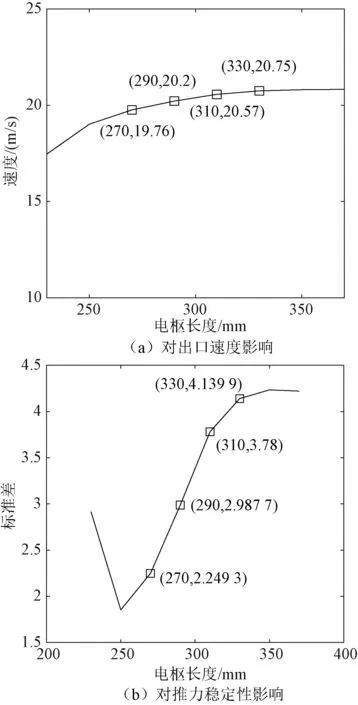
图16 电枢长度对出口速度和推力稳定性影响Fig.16 Influence of armature lengths on muzzle velocity and force stability

随着电枢长度的增加，载荷出口速度增加，这是由第一峰值推力的增加所致，当长度增加到330 mm后，再增加长度载荷出口速度基本没变化，从表4可以看出，330 mm后第一峰值推力也基本不再增加；电枢长度在250 mm时，推力曲线标准差最小，推力最稳定，电枢长度大于250 mm后，随着电枢长度的增加，推力曲线标准差不断增大，推力稳定性变差。

在实际推射载荷时，电枢长度每增加20 mm，电枢质量会增加0.087 kg，假设连接机构质量不变，则有效模拟载荷质量会减少0.087 kg，相比于3.5 kg的标准模拟载荷，重量减少了2.5%，如果速度不能提高1.6%，则系统整体发射效率会降低，因此，从有效载荷发射效率角度考虑，本系统电枢长度不宜超过310 mm。

3.4 电枢厚度对推力稳定性影响

和改变电枢长度一样，改变电枢厚度也会改变电枢重量，从而影响整个推射载荷重量。采用和电枢长度相同的研究方法，通过改变连接结构和模拟载荷重量来保持整个推射载荷重量不变，电枢外径保持不变，通过改变电枢内径来改变电枢厚度，电枢厚度取2～10 mm进行研究，图17为电枢厚度在3 mm、5 mm、7 mm、9 mm下的推力曲线。

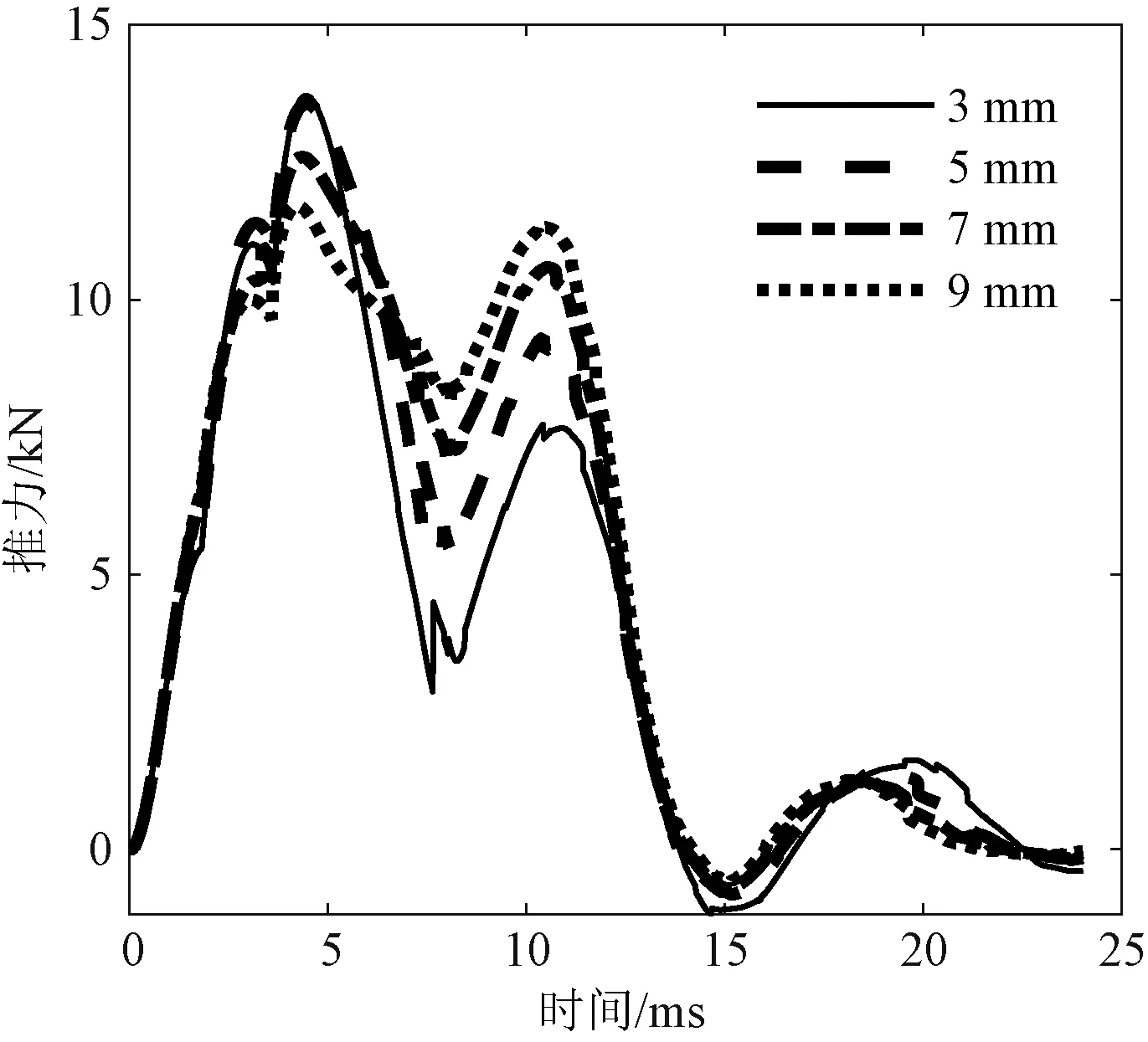
图17 不同电枢厚度下推力曲线Fig.17 Force curves of different armature thicknesses

表5对不同电枢厚度下推力曲线的双驼峰峰值大小及发生时刻、波谷值大小及发生时刻、推射速度进行统计。

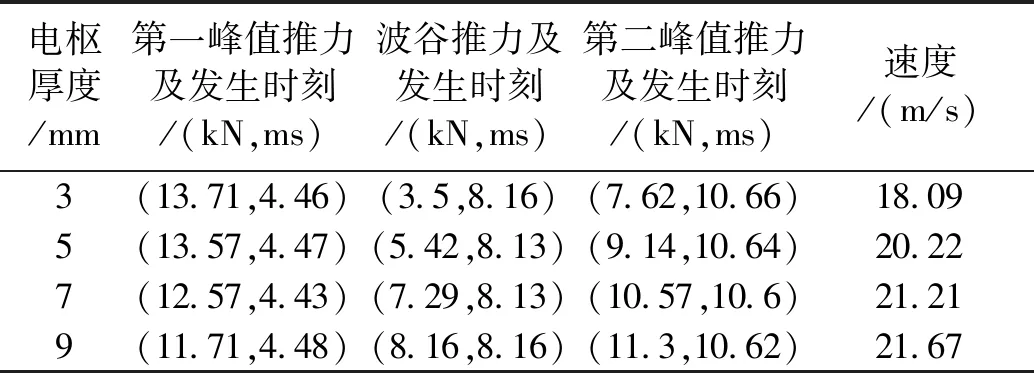
表5 不同电枢厚度对推力特性和出口速度的影响Tab.5 Influence of different armature thicknesses on force characteristics and muzzle velocity

增加电枢厚度，第一峰值推力略有减小，但是可以大幅度增加波谷推力和第二峰值推力;各个峰值时刻和波谷时刻基本保持不变。

图18为3 mm厚电枢和9 mm厚电枢在第二峰值推力时刻10.6 ms时，驱动线圈和电枢的电流密度分布云图来分析不同电枢厚度对推力的影响。

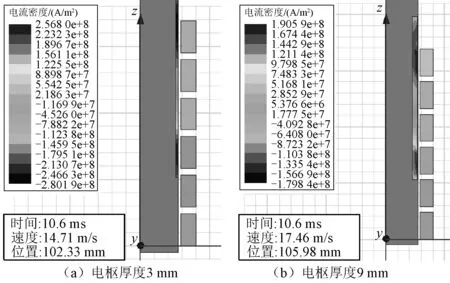
图18 10.6 ms时驱动线圈与电枢电流密度分布Fig.18 Current density distribution of drive coils and armature at 10.6 ms

3 mm厚电枢的截面较小，感应电流分布趋于饱和，当达到铝材料的载流极限后就不会增加，而9 mm厚电枢截面大，可以承载更大的感应电流，而在相同的磁场环境下，拥有更大电流的载流体就会受到更大的电磁力。

图19为电枢厚度对载荷出口速度和推力稳定性的影响关系图。

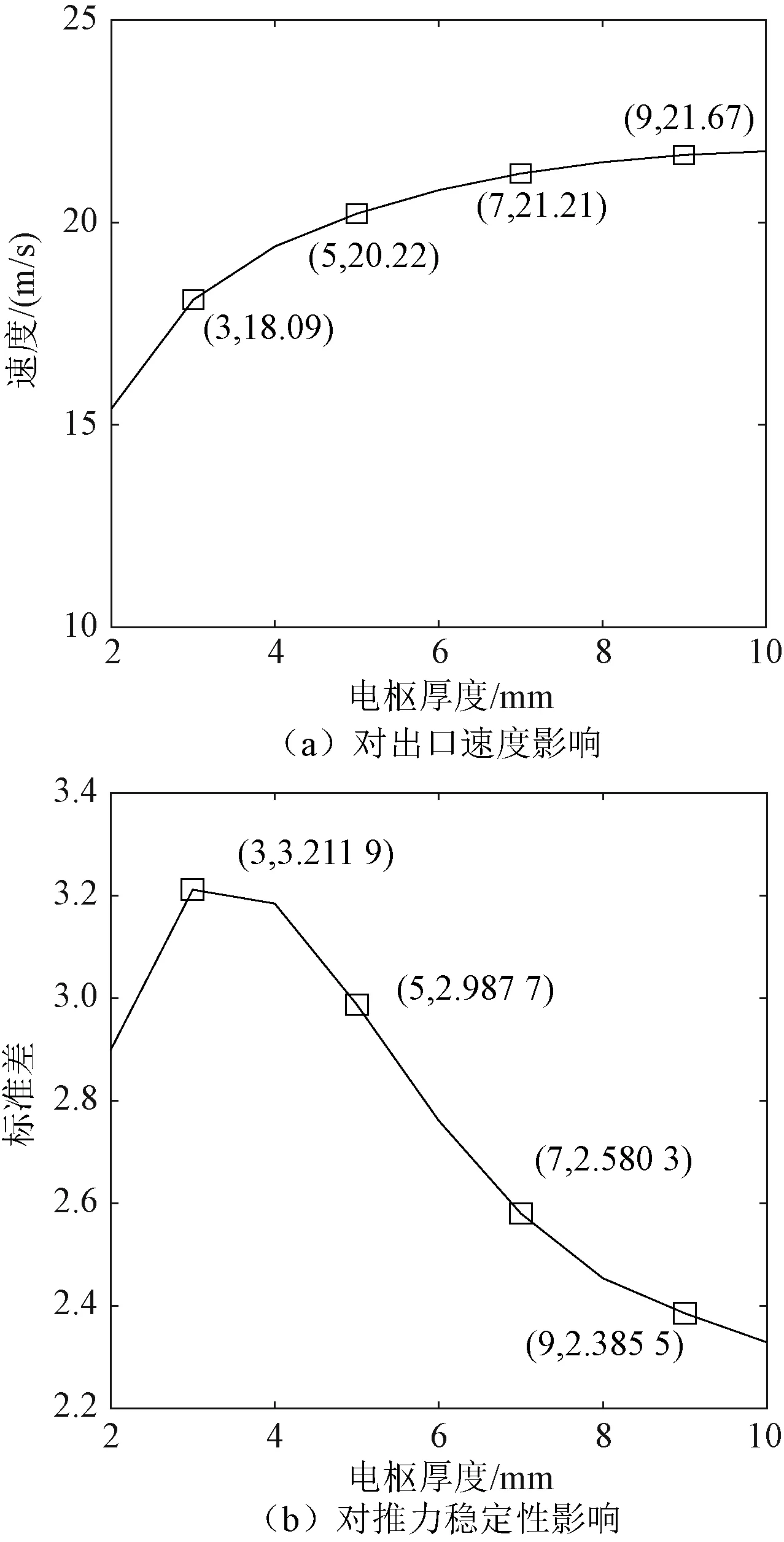
图19 电枢厚度对出口速度和推力稳定性影响Fig.19 Influence of armature thicknesses on muzzle velocity and force stability

电枢厚度在3～10 mm之间，随着电枢厚度增加，载荷出口速度提高，推力曲线标准差也减小，推力稳定性不断提高。由此可知，增加电枢厚度可以同时提高载荷出口速度和推力稳定性。但是，和增加电枢长度一样，电枢厚度增加也会增加电枢重量，在保持整个推射载荷重量不变的前提下，会减小有效载荷的重量，从而降低有效载荷发射效率。因此，在实际选择电枢厚度参数时，必须综合考虑载荷出口速度、效率、推力稳定性等发射要求，选取最优厚度参数。