基于WPD和双重注意力机制TCN的短期电价预测
2022-07-01魏云冰童东兵
黄 圆,魏云冰,童东兵,徐 浩
(上海工程技术大学电子电气工程学院,上海 201620)
1 引言
电价是对竞争激烈的电力市场运营状况及交易结果最直接的反映,因此,精确的短期电价预测有助于电力系统优化调度,帮助市场主体制定合理的竞价决策,从而达到利益最大化、成本最小化和风险最低化。
电价预测主要采用传统方法和人工智能方法等[1]。传统方法主要包括自回归方法[2]、广义自回归条件异方差方法[3]和灰色预测方法[4]等。随着人工智能在各个领域中得到广泛的应用,支持向量机(Support Vector Machine,SVM)[5]、随机森林[6]、长短期记忆网络(Long Short-Term Memory,LSTM)[7-10]等模型在电价预测中表现较为出色。文献[11]采用改进多层级门控LSTM,虽然解决了梯度爆炸问题,并增强了提取和分析电价序列特征的能力,但LSTM不能进行并行运算,导致预测耗时较长。随着人工智能的发展,具有可并行计算结构优势的时间卷积神经网络(Temporal Convolutional Network,TCN)可以有效解决上述问题。TCN神经网络已经在工业过程故障预测[12]、风电功率预测[13]等领域取得了较好的表现。
虽然TCN模型为时间序列预测提供了思路,但在电价预测时存在忽略实际运行中各输入特征的关联性,并且TCN在处理历史信息上表现较差,因此,需要对TCN进行优化处理。由于注意力机制模型在衡量输入特征的重要程度上已经取得了较好的效果[14],所以在利用TCN模型预测电价时引入特征和时序2个维度注意力机制。首先,在输入侧引入特征注意力机制TCN(Feature Attention mechanism based TCN,FA-TCN),挖掘电价与其影响因素输入特征之间的关联性,突出关键输入特征;其次,在输出侧引入时序特征注意力机制TCN(Temporal Attention mechanism based TCN,TA-TCN),挖掘不同历史时刻对待预测时刻的重要性,获取历史关键时刻点信息。
由于电价时间序列的高频和非平稳性,对数据进行预处理能够提高预测精确度[15]。小波包分解(Wavelet Packet Decomposition,WPD)[16]能够很好地处理带有高频信号的数据,被广泛应用于各种模型的数据处理阶段。
本文提出一种基于WPD和双重注意力机制TCN(Dual-stage Attention mechanism based TCN,DA-TCN)的短期电价预测模型。采用WPD剔除电价数据中高频噪声部分;再将经过WPD处理过后的电价数据与其影响因素数据输入TCN网络进行预测,引入双重注意力机制突出关键输入特征及历史关键时刻信息的影响力;最后,进行实例仿真实验,结果表明本文方法在电价预测中精度更高、稳定性更好。
2 小波包分解与重构算法原理
小波包分析相较于小波分析进步之处在于其可以对全频进行分解,并且分解结果更为精细。
尺度函数φ(t)和小波函数ψ(t)两者的关系可表示为:
(1)
进一步递推,定义下列公式:
(2)

(3)

小波包分解的实质是随机利用共轭正交滤波器将信号分割到不同频段上,每经过一次滤波,信号长度就减少1/2。
(4)
而在对复杂的非线性电价序列进行小波包分解重构时,应先确定适合的小波基函数和分解层数,以实现对电价序列的去噪处理。
3层小波包分解示意图如图1所示。图1中原始电价序列S分解为S(1,0)和S(1,1),S(1,0)继续分解为S(2,0)和S(2,1),以此类推,逐层分解,则经过M层小波包分解后的电价序列可表示为:

图1 3层小波包分解图Fig.1 3-layer wavelet packet decomposition diagram
S=S(M,0)+S(M,1)+…+S(M,2M-2)+S(M,2M-1)
(5)
式中,S(M,0),S(M,1),…,S(M,2M-2),S(M,2M-1)分别为信号经过M层小波包分解后的子频带电价序列。
本文进行小波包分解重构短期电价序列的步骤为:①确定最优小波基;②选用合适的分解层数,确定分解层数;③设定适用电价序列分解的小波包分解系数的阈值;④根据电价序列的分解特征信息和系数进行小波包分解重构。
3 基于DA-TCN的预测模型
3.1 TCN网络
TCN网络融合了一维卷积网络、扩张卷积和因果卷积,在时间序列预测问题上拥有很好的表现。TCN中的卷积网络具有可并行计算的特性,能够有效解决耗时过长的问题。
TCN网络应用于短期电价预测的任务中,主要具有以下特点:①为满足短期电价预测的要求,TCN网络具有时间因果性,即当前模型输出只与过去相关而与未来无关;②适用于短期电价的TCN网络的输出序列长度可任意调整;③多层TCN网络虽深度浅但记忆距离长。
TCN因果扩张卷积结构如图2所示。TCN的扩张卷积结构最特殊之处在于其具体形式由卷积核和扩张系数决定。卷积核和扩张系数分别从网络上层输入元素的个数和距离两个角度改变TCN网络的形式。图2中,设网络输入为x=[x1,x2,…,xk],输出为y=[y1,y2,…,yk],扩张系数p随着网络深度呈指数性增大,即p=2r,r为网络层数,且扩张系数越大,信息提取范围就越大。因此,TCN卷积通过搭建相对较少的层,就能获得相对较大的感受野。

图2 TCN因果扩张卷积结构Fig.2 Causal dilated convolutional structure of TCN
TCN网络神经元的感受野,即网络记忆长度,由卷积核大小、扩张系数和卷积层数决定,则扩张卷积运算后的第s个运算值为:
(6)
式中,x为输入序列;“*”为卷积运算;u为卷积核大小;f(i)为卷积核中的第i个元素[17];xs-p·i为输入序列中与卷积核相对应运算的元素。
为满足电价预测中的时间因果关系,对每层卷积层进行零填充,以保证输出张量与输入张量具有相同的长度。为使TCN的扩张卷积更符合电价预测要求,在网络每层引入填充系数来保证因果卷积。填充系数可描述为:
qr=(r-1)p
(7)
式中,qr为填充系数。
TCN残差模块包含基础的TCN因果扩张卷积层、权值规范化层(Weight Norm)、激活函数Relu和Dropout层,N个残差模块结构如图3所示。

图3 残差块结构Fig.3 Structure of residual block
权值规范化可以消除梯度爆炸问题,并且能有效加快计算速度;为使TCN网络具有非线性且不过于简单,采用Relu激活函数,在Relu激活层后加入Dropout层来防止过拟合,以此达到正则化效果。通过1×1的卷积调整残差张量维度不同的问题。
3.2 注意力机制
注意力机制源于对人脑如何分配注意力的模拟,与神经网络结合的具体表现为改变隐含层的特征权重[18]。注意力机制对影响结果较大的关键特征赋予更多的权重,减少甚至忽略其他影响较小的非关键特征的权重,以此提高模型的合理性与稳定性。
3.2.1 FA-TCN预测模型
将输入的负荷、发电量、温度、湿度和日类型的时序序列数据设为X=[x1x2…xK]T=[x1x2…x5],展开可表示为:
(8)

为获取不同因素对电价的影响程度,即权重大小,采用特征注意力机制来量化权重,其结构如图4所示。
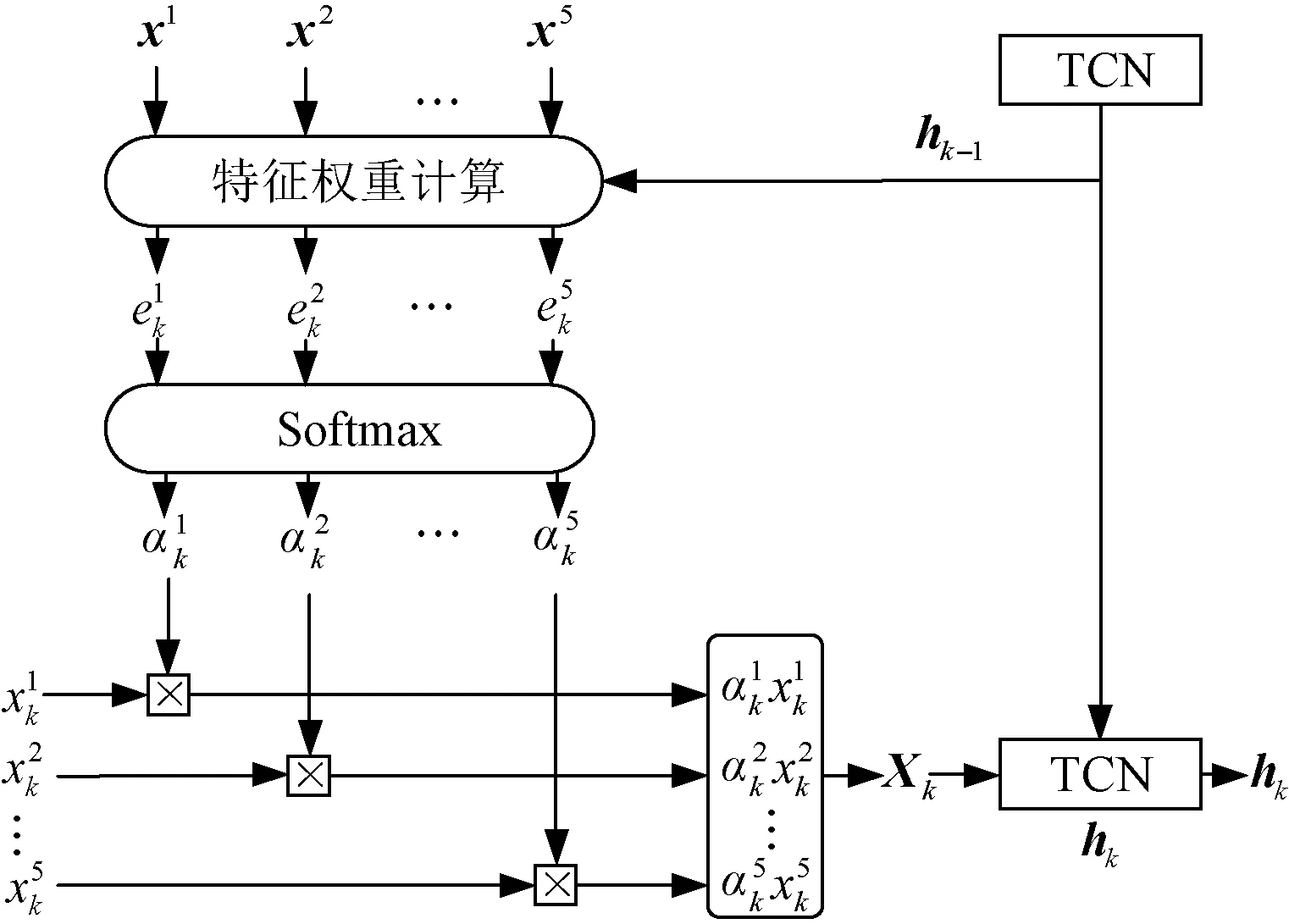
图4 特征注意力机制Fig.4 Feature attention mechanism
特征注意力机制的输入由时间序列特征值、前一时刻神经网络隐含层的状态值hk-1和当前时刻输入特征xn组成。特征注意力机制的计算公式可表示为:
(9)
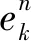
对其进行归一化处理,计算公式如下:
(10)
(11)
隐含层状态值hk则更新为:
hk=f1(hk-1,Xk)
(12)
式中,f1为TCN网络单元,输入为考虑关联度大小的加权特征值。
特征注意力机制在短期电价预测中表现为通过多层感知机分析出不同输入参量对预测信息的重要程度,量化电价影响因素(负荷、发电量、温度、湿度和日类型)输入特征影响力的权重,突出关键特征,弱化相关度较小的特征。
3.2.2 TA-TCN预测模型
经过TCN网络得到的电价预测值随着时间序列的增加,其预测结果会越发不准确,因此在TCN网络输出侧加入时序注意力机制,挖掘与电价相关的历史时间序列状态信息,获取相应的权重以及对当前时刻电价数据的影响程度,其结构如图5所示。
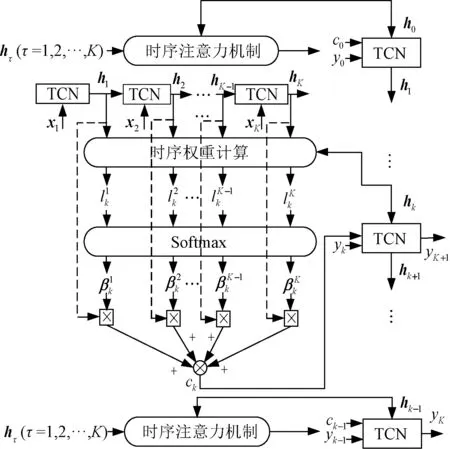
图5 时序注意力机制Fig.5 Temporal attention mechanism

(13)
式中,Vd和Wd为时序注意力机制神经元权重;Ud为偏置项。

(14)
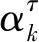
(15)
将电价数据yk与ck结合作为TCN网络的预测输入y′k,即:
y′k=W′[yk;ck]+b′
(16)
式中,W′和b′分别为TCN网络前端融合输入的权重和偏置。
时序注意力机制计算了历史关键时刻信息的权重,得到k时刻隐含层状态值h′k:
h′k=f1(h′k-1,y′k-1)
(17)
则预测结果,即K+1时刻电价数据yK+1可表示为:
(18)
式中,Wy和bw分别为TCN网络权重和偏置;Vy和by分别为整个网络在维度变换前的权重和偏置;θ为网络参数的集合,采用梯度下降法求解[19]。
时序注意力机制在短期电价预测中充分考虑电价情况受历史状态影响比较大且不同时刻的电价情况影响力不同等问题,通过量化每一历史时刻状态信息对当前预测结果的影响程度,自适应处理历史状态信息,强化相关时刻状态信息的影响力。
4 短期电价预测模型
电价高频特性的存在往往使得预测模型表现不佳,预测精度难以提高,因此,需对预测模型的输入进行数据预处理。而小波包分解相较于小波分解适用于电价序列的特点在于其可对电价序列全频进行分解,并且能够自适应地选择相应频带与电价序列频谱相匹配,能够很好地解决电价序列存在的高频噪声,掌握并保留细节信息,提高电价序列的时域分辨率,从而降低电价序列噪声部分对预测模型的干扰,提升预测效果。
此外,由于电价序列的高波动性,非线性和不规则性的特点,相较于传统模型在掌握特征和处理电价序列的不规则性方面表现较差,而深度学习对复杂问题具有普遍的适应性,并具有突出捕捉特征的能力。TCN网络在时间预测问题中拥有很好的效果,能够有效地解决梯度消失或者梯度爆炸问题,并且具有并行计算、低内存消耗和通过改变感受野来控制序列记忆长短等优势,更适用于电价预测。但TCN网络在实际应用中往往会忽略各输入特征的关联性且在处理历史信息上表现较差,而在实际生活中电价会随着电力生产量、电力消费量等要素的变化而变化,且电价受历史价格影响较大,忽略历史电价信息将导致预测精度不佳。因此,为解决TCN网络的缺陷并探索电价的变化规律,在TCN网络基础上引入双重注意力机制,自适应挖掘并量化电价相关影响因素,以及历史电价状态信息与电价的内在联系,突出关键影响因素和关键历史时刻电价信息的影响力,从而提高TCN网络预测的精确度。
基于上述分析,本文提出一种基于小波包分解和双重注意力机制TCN短期电价预测模型,模型具体流程如图6所示。
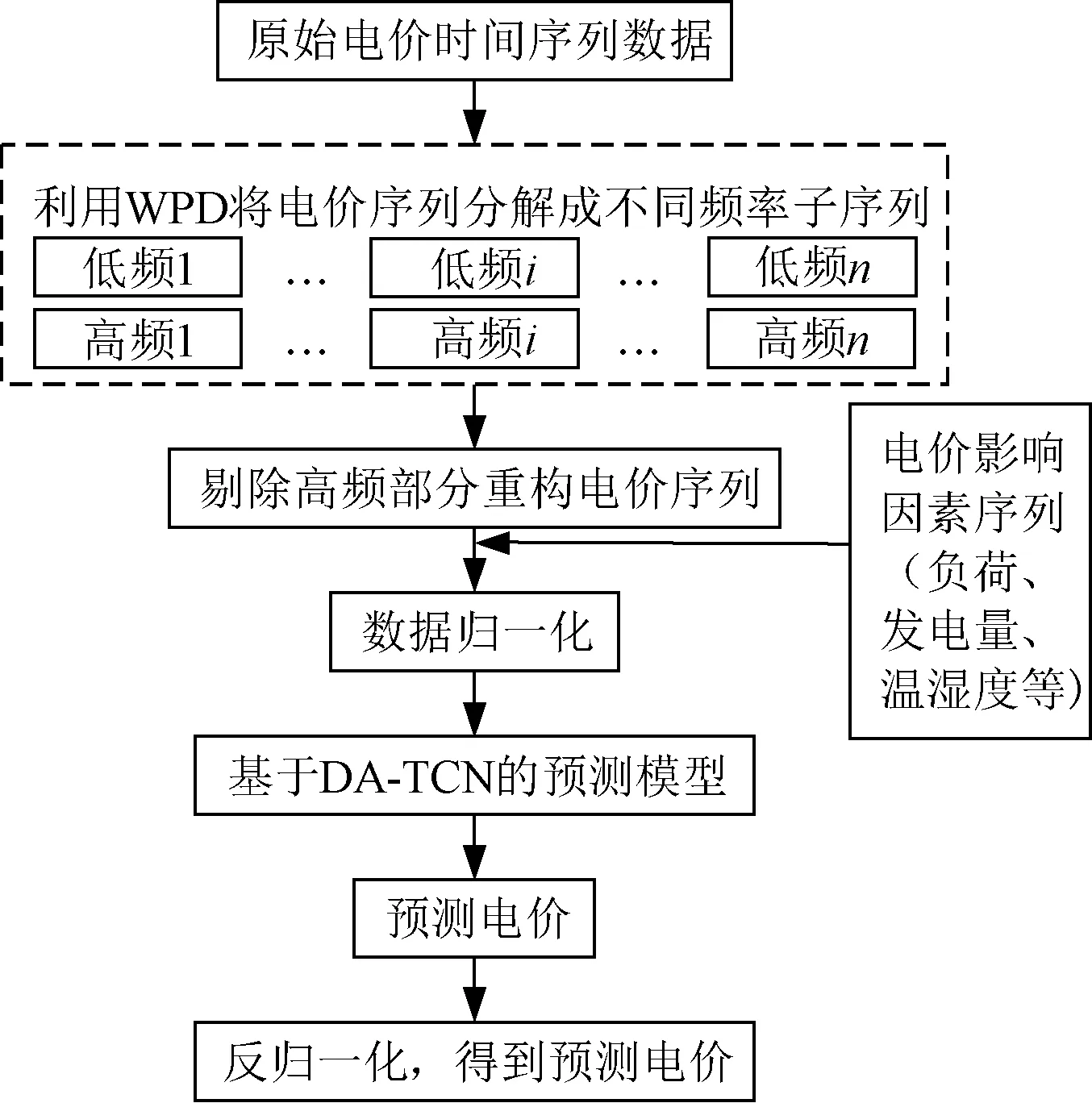
图6 DA-TCN模型流程Fig.6 Flow chart of DA-TCN model
预测模型主要分为4个步骤。
(1)利用WPD方法对电价数据进行分解,得到n个低频和高频子序列。
(2)对不同频率的子序列进行重构处理,剔除高频部分,再将剩余序列重构成新的电价序列。以此来减少高频噪声和随机波动数据对模型预测精确性影响。
(3)在新的电价及其影响因素序列进行预测模型之前,应先对其进行归一化处理,将数据映射到[-1,1]上,公式为:
(19)
式中,x为原始数据;xmin为x的最小值;xmax为x的最大值;x′为归一化后的值。
(4)对归一化后的电价数据构建TCN预测模型,引入双重注意力机制,在输入侧引入特征注意力机制TCN,挖掘电价与其相关影响因素特征量之间的关联性;在输出侧引入时序注意力机制TCN,突出关键历史时刻点信息。利用梯度下降法求解网络模型的参数,建立基于DA-TCN预测模型。最后,再将DA-TCN模型的预测输出值反归一化得到预测电价数据。
5 实例分析
本文选取2018年1月1日~2018年4月2日澳大利亚新南威尔士州电力市场实时数据作为数据集(数据来源:https://www.aemo.com.au)。数据采集频率为每半小时1次。每个时刻数据包含电价($/(MW·h))、负荷(MW)、发电量(MW·h)、温度(℃)、湿度(%)和日类型(工作日为1,休息日为0)。
5.1 小波包分解重构电价结果
在进行WPD分解重构之前,应先确定小波基函数,选择合适的小波基函数能够使去噪效果更好。目前普遍采用的小波基函数主要有Haar、Dmey、CoifN、BiorNr.Nd、和SymN等小波基函数。为确定适合本文电价数据的最优小波基函数,现采用不同小波基函数进行小波包分解重构,计算其信噪比和相关系数来评价各小波基函数,评价指标结果见表1。
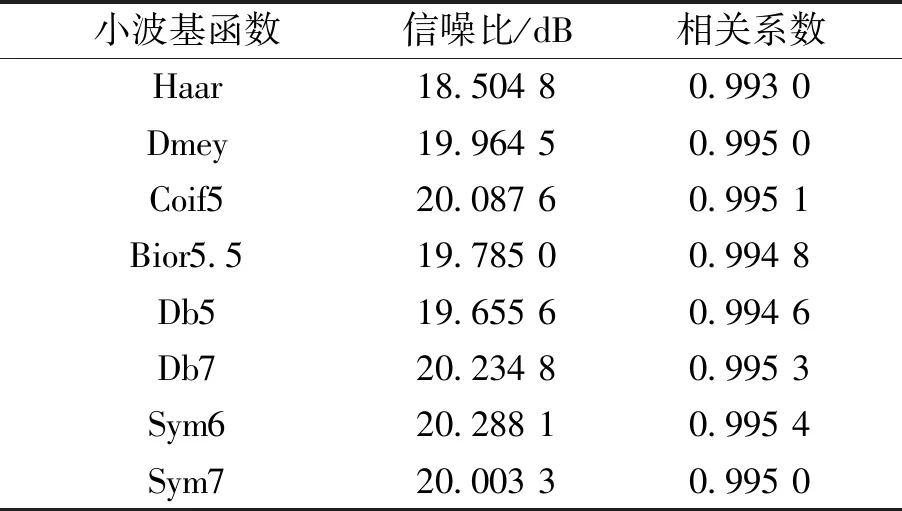
表1 各种小波基函数的评价指标Tab.1 Evaluation metrics for various wavelet basis functions
从表1中可以看出:不同小波基函数处理电价数据具有不同的信噪比和相关系数。经过Sym6小波处理后的电价数据信噪比和相关系数都为最大,说明去噪效果好且去噪后的数据和原始数据关联性大。分解层数影响着去噪效果。分解层数过少,将导致数据中只有少部分的高频数据被分解出来[20],但分解层数太多也会去噪过度,导致有用信息被去除。因此,本文采用Sym6小波基函数,默认阈值,进行3层小波包分解处理,具体波形如图7所示。
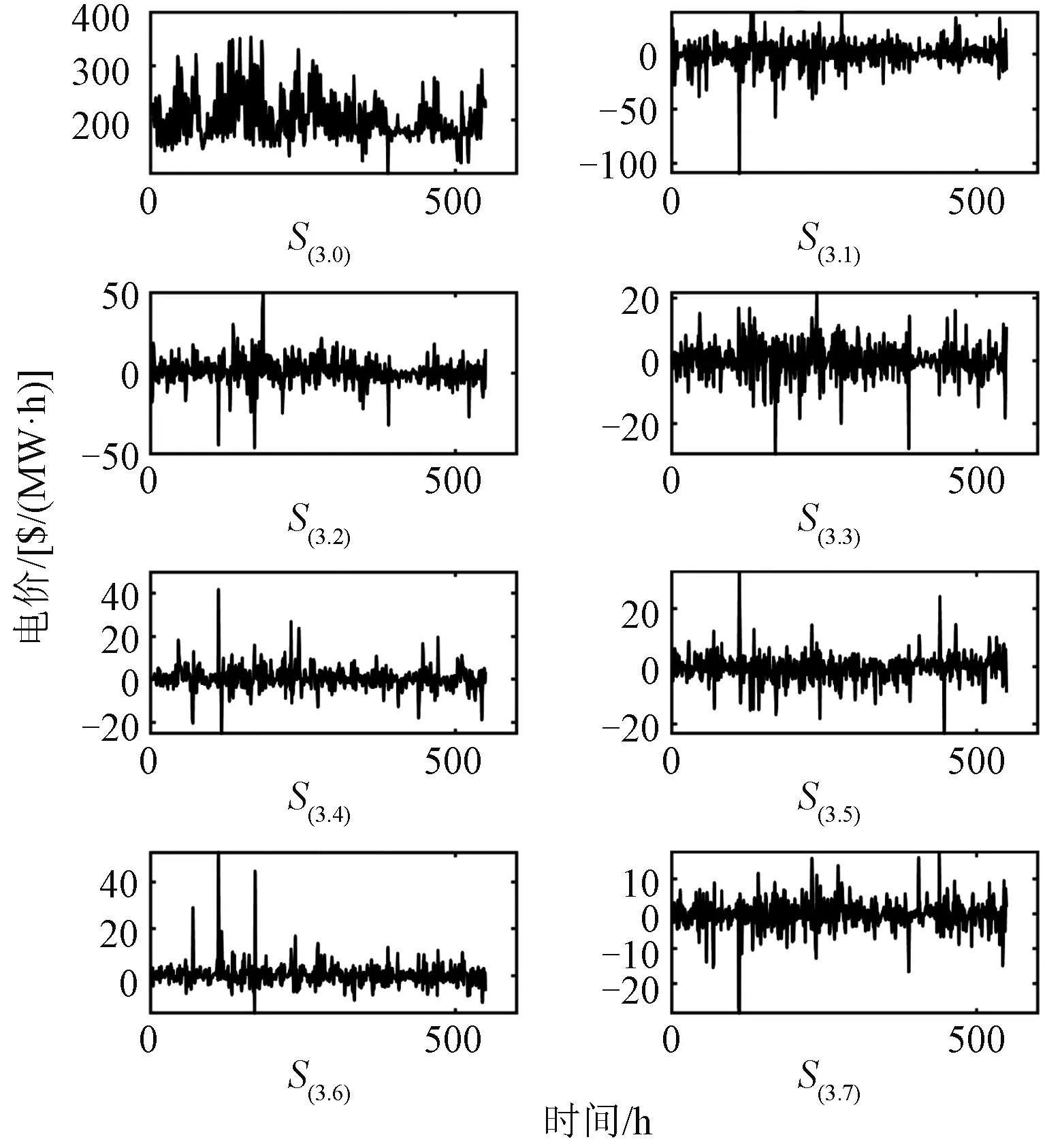
图7 不同频段下的电价波形Fig.7 Electricity price waveforms at different frequency bands
图7中,S(3,7)为小波包分解出得到的最高频部分,其中包含了大量随机波动和噪声部分,这些部分会对预测造成较大的影响,因此将其剔除。将剩余的7个子序列重构成新的电价序列,作为新的样本集与影响电价的相关数据共同输入到双重注意力机制的TCN预测模型中进行训练学习。
5.2 基于DA-TCN的预测结果
为了提高建模的准确度,对实验数据进行划分,将2018年1月1日~4月1日电价及其影响因素数据作为训练集,4月2日24 h的电价作为测试集,并对电价及其影响因素数据进行归一化处理。实验中基于TCN网络的模型设置输入维度均为6,输出维度为1;卷积核大小为2;batch size设为32,Dropout取0.2,残差模块个数为6;在注意力机制中,设置3层隐含层,每层隐含元个数为5,T设置为50,在时间注意力机制中,设置3层隐含层,时序隐含元个数设置为50。学习率设置为0.001,批尺寸设置为30,epoch设置为100。所有模型优化算法均为Adam,损失函数均为均方误差(Mean Squared Error,MSE)。
评价指标采用均方根误差(Root Mean Square Error,RMSE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE),计算公式为:
(20)
(21)
式中,N为预测点个数;yk为第k个真实值;y′k为第k个预测值。
5.3 预测结果分析
5.3.1 注意力机制预测结果分析
为了对DA-TCN模型性能进行分析,设经过WPD处理后的电价序列及其影响因素数据为输入,将DA-TCN模型预测结果与TCN模型、FA-TCN模型、TA-TCN模型的预测结果进行对比。各模型整体预测的评价指标值见表2,各模型24 h预测结果曲线图如图8所示。
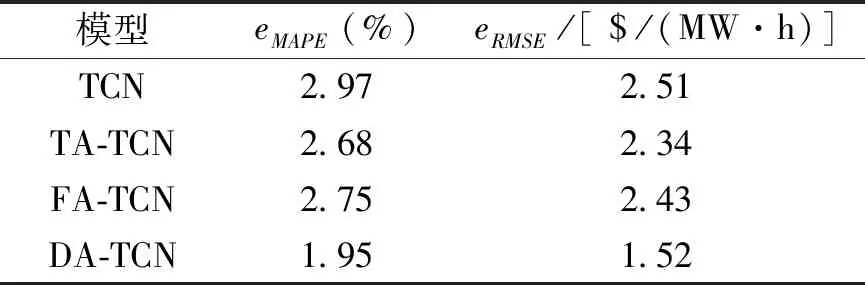
表2 各模型预测误差对比Tab.2 Comparison of prediction error between different models

图8 24 h电价预测曲线Fig.8 24-hour electricity price prediction curve
由表2可以看出,DA-TCN模型的eMAPE值为1.95 %,相比于TCN、TA-TCN和FA-TCN分别减少了1.02 %、0.73 %和0.80 %,eRMSE值也比其他的模型要小,说明DA-TCN模型具有较好的普适性,能够很好地适用于一天24 h电价变化规律,该模型还拥有较强的鲁棒性和稳定性,更符合实际情况。由图8可看出,DA-TCN模型在24 h电价预测中表现优异,预测电价曲线与实际曲线最为贴合。
结合表2和图8对比分析可知,相比于TCN模型,FA-TCN预测模型关联了各种因素特征量对电价的影响权重,不但将各影响因素的权重平均化,而且在各个时刻自动挖掘负荷、发电量、温度、湿度及日类型对电价的权重,并对各影响因素的权重进行量化修正处理,突出关键影响因素,从而提高了预测精度。对比TCN模型、FA-TCN模型和TA-TCN模型可发现,TCN模型和FA-TCN模型预测的24 h电价曲线与实际曲线都有不同程度的偏差,但TA-TCN通过对提前一天时间序列信号的加权,在整体和关键时刻点预测值都与实际值接近。显然,由预测结果及误差分析得出,双重注意力机制既挖掘了输入特征的权重,又考虑了时间序列数据间的依赖关系,在短期电价预测中取得了较好的表现。
各模型24 h电价预测相对误差对比如图9所示。

图9 24 h电价预测相对误差曲线Fig.9 Relative error curve of 24-hour electricity price forecast
从图9中可以看出,DA-TCN模型整体误差远低于其他模型,效果最好,没有引入注意力机制的TCN模型在很多时刻误差较大,整体误差曲线的波动也较大,表现最差。在某些关键时刻点,辟如8:00、17:00和20:00等时刻,DA-TCN模型表现最好,TA-TCN模型误差也很小,FA-TCN模型和TCN模型表现较差,这是由于时序注意机制连接了历史关键时刻信息,保证了关键时刻预测表现,而FA-TCN模型只是突出了关键特征的影响,并不能记忆历史时刻信息,在短时预测方面稍逊于TA-TCN模型。结合了两种注意力机制的DA-TCN模型在整体预测及关键时刻点预测都表现优异,误差曲线也较为平稳。
5.3.2 特征关联性分析
为验证特征注意力机制挖掘各特征量的关联性,对训练完成的模型进行实验,提取某日24 h的特征分析情况。关联热力图如图10所示。每个小格的颜色深浅代表电价与对应特征的关联性大小。颜色越深,表示该特征权重系数越大,关联性越强;颜色越浅,表示该特征权重系数越小,关联越弱。

图10 电价关联特征热力图Fig.10 Association heat map of load electricity price
由图10可以看出,负荷对应的热力图颜色最深,与电价的关联性最大,其次是发电量和日类型,而温度和湿度对电价的影响相对较弱,但在午间时分,温度与电价的关联性显著增大,此时的实际电价也增高,这与电价实际情况一致。显然,通过特征注意力机制可有效提取各特征量信息。
5.4 预测性能对比
为验证本文方法的有效性,采用SVM、LSTM以及DA-TCN模型进行对比实验分析,其中SVM采用径向基函数;LSTM网络设置输入维度为6,输出维度为1;隐含层维度和时间步长为10的单层隐含层。分别进行单独预测模型以及与WPD组合预测模型实验,其预测结果见表3。

表3 各模型预测性能Tab.3 Prediction performance between different models
由表3可知,相比于LSTM、TCN、DA-TCN模型,WPD+LSTM、WPD+TCN、WPD+DA-TCN模型的预测精度都有一定的提高,不仅说明了WPD方法能够有效剔除高频噪声部分,还证明了数据预处理融合组合预测方法的预测性能优于单个预测模型。本文所提方法预测的eRMSE为1.52 $/(MW·h),eMAPE为1.95 %,误差远小于不考虑注意力机制且未使用WPD处理的TCN模型(eMAPE为3.69 %,eRMSE为3.27 $/(MW·h))。相比于其他6种模型,本文方法无论是预测精度还是模型平稳性方面表现最优,预测结果与实际电价最为接近。
6 结论
针对电力市场中电价受诸多因素影响以及电价数据本身的高频、非平稳性等问题,本文提出了一种基于WPD和双重注意力机制TCN的短期电价预测模型。首先采用小波包分解重构电价序列,很好地减少了噪声信号对模型预测的干扰。然后在TCN预测模型中引入双重注意力机制,很好地解决了TCN模型在电价预测时存在忽略实际运行中各输入特征的关联性,以及在处理历史信息上表现较差的问题。特征注意力机制挖掘电价与其影响因素的相关性,优化TCN模型的输入,提高整体预测精度;时序注意力机制挖掘当前时刻电价与历史关键时刻信息的关联度,优化TCN模型的输出,提高了关键时刻点预测精度。经实验对比验证,本文所提模型误差均小于对比模型,预测结果更接近真实值,在短期电价预测的应用中得到了初步验证,并取得了较好的效果。
