基于频率法的吊杆索力测试及影响因素研究

2022-07-01孙恒飞赵思桐

内蒙古公路与运输 2022年3期

孙恒飞，王曈，沐波，赵思桐

（1.交通运输部科学研究院，北京 100029；2.交科院公路工程科技（北京）有限公司）

1 引言

近年来，为了满足交通运输需求的不断增长，桥梁事业迅猛发展，桥梁跨度不断增大，结构形式也由简到繁。与此同时，桥梁建设与运营过程中事故时有发生。如2001年11月7日宜宾南门长江大桥发生吊杆与桥面部分断裂事故，造成3 死5 伤；2006 年12 月9 日北京顺义一座景观悬索桥进行荷载试验时突然坍塌，造成3人受伤；2011年4月12日新疆孔雀河大桥主跨第二根吊索断裂，造成桥面塌陷，6人受伤；2011年7月14日福建武夷山公馆大桥运营过程中因吊杆突然断裂，造成1死22伤。因此，完善桥梁结构设计，重视桥梁施工与运营过程中的每一个环节，是确保桥梁建设和运营安全的重要内容。吊杆作为桥梁的重要结构之一，对吊杆索力的精确测试与控制是中、下承式拱桥施工与运营过程中的关键步骤。

毛亚娜等[1]基于弦振动理论，根据系杆拱桥吊杆的振动特性，得出了频率法测试吊杆索力的实用计算公式，研究表明将吊杆两锚固点间长度减去两端连接部分长度的一半取值计算，将会得到较为合理且精确的结果，并得出了短吊杆的弯曲刚度不容忽视，其影响随着吊杆长度的减小而增大的结论。贾佳等[2]基于振动频率法，直接给出公式，将吊杆两端默认为等效铰接计算，通过对比吊杆两端固结与两端铰支计算结果，得出可以采用等效铰接计算方法来修正吊杆计算长度与抗弯刚度的影响。倪应谦等[3]通过采用在吊杆中间附加质量块的方法，建立了吊杆中部附加质量块前后拉索的振动平衡方程，得到吊杆等效计算长度，进行了质量块对索力的敏感性分析与测试。燕启清等[4]结合吊杆索力与其震动频率之间的关系，引入边界条件修正系数与杆索力偏差系数来修正吊杆两端边界条件及短吊杆的界定，以此提高吊杆索力测试与计算的精度。韩亮亮等[5]利用MATLAB 软件对索长修正系数进行公式化拟合，结合有限元计算分析得到吊索的计算索长并引入了修正系数，以此快速便捷的计算吊杆索力。

上述研究并未对吊杆的计算长度进行定性的分析，只是估算或直接给出经验公式，并未考虑计算过程中抗弯刚度的影响。因此，开展基于频率法的吊杆索力测试及影响因素的研究十分必要。本文以衡水衡武大桥（90m跨下承式钢拱桥）吊杆索力测试为例，基于弦振动理论的频率法，对施工过程中吊杆的索力进行精确的测试与计算，探究影响索力测试精度的因素及规律，以期为同类桥梁吊杆索力的精确测试提供参考。

2 弦振动理论

根据弦振动理论，张紧的拉索动力平衡方程为[6]：

如果索的两端固结或一端铰接一端固结,方程解的形式为超越函数;如果索的两端为铰支,那么方程的解为:

3 工程概况

衡水衡武大桥为下承式钢箱系杆拱桥，计算跨径为87.2m，矢高为21.8m，拱轴线线型为二次抛物线。主桥每侧拱肋各设置18 根吊杆。吊杆索体采用双束GJ15-12 钢绞线整束挤压拉索，抗拉强度标准值fpk=1860MPa，弹性模量Ep=1.95×105MPa，截面惯性矩I=1.17799×10-6m4。吊索上端均锚固于主拱内，下端铰接于主梁上。吊杆从U形桥台到墩形桥台编号依次为左幅1#～18#与右幅1#～18#，图1为全桥构造示意图，图2为吊杆索体构造图，构造图来源于相关施工文件。

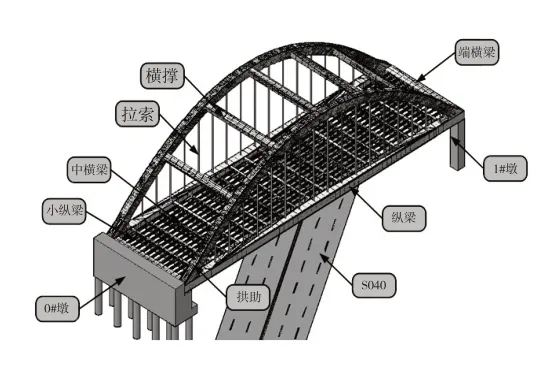
图1 全桥构造示意图

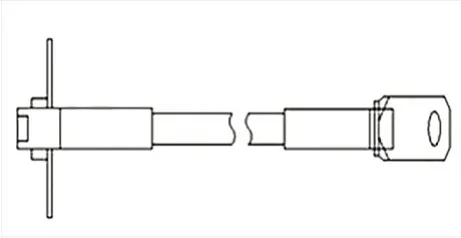
图2 吊杆索体构造示意图

4 索力测试影响因素

4.1 索力测试精度的影响因素

频率法测试吊杆索力的原理是弦振动理论，目前绝大多数频率法技术采用的索力求解公式为公式（3），而采用公式（3）进行索力求解的前提是将影响吊杆边界约束默认为两端铰接并且忽略抗弯刚度，这样频率采集器采集的频率会在电脑软件中生成频谱图，再对吊索长度与单位索重进行定义就可以得到索力。当采用基于弦振动理论的频率法进行吊杆索力测试时，在精确获得吊索频率的前提下，影响索力测试精度的因素有边界约束和抗弯刚度。

由于上述两个因素的影响，当输入设计吊索长度与单位索重时，不能准确测得实际索力。对于边界约束的影响，可以通过修正吊索的计算长度来消除；对于抗弯刚度的影响，应找出受抗弯刚度影响较大的索长边界值，以为索力的测试与计算提供参考[7-9]。

4.2 边界约束对吊杆的索力影响

衡水衡武大桥上端为张拉锚固端锚固于拱肋内，下端铰接于主梁上，不满足两端铰支。所以应对吊杆的计算长度进行逐一修正来消除边界约束的影响，具体做法为：在进行吊杆张拉施工的过程中，当每根吊杆用油压千斤顶张拉至设计值后，用频率采集仪采集频率，然后将张拉设计值与采集每根张拉吊杆的频率代入公式（2）中反算得到吊索长度，即为修正后的吊索计算长度。以此类推，最后张拉并调整完所有吊杆索力后，再重新测定所有吊杆的频率，并将修正后的吊杆长度一并代入频率法公式进行索力计算，可以精确地测量出全桥吊杆的实际索力。

本文典型算例为全桥吊杆特征的左幅2#～9#内侧吊杆测定结果，修正后的吊杆长度见表1。

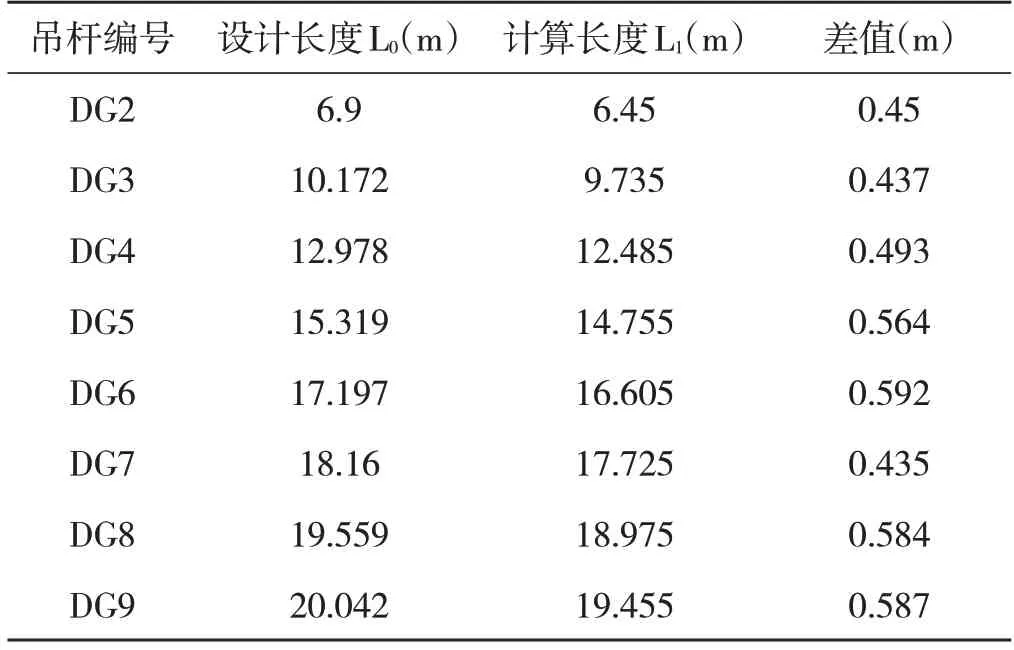
表1 吊杆实际长度与计算长度一览表

采用最小二乘法理论对吊杆设计长度与计算长度进行线性拟合，得到残差平方和为0.01969，相关系数为0.99993，校正决定系数为0.99985，拟合效果良好，如图3 所示。由此可知，当吊杆两端固结默认为两端铰支时，吊索设计长度与计算长度的关系式为L1=0.99L0-0.37，其中L1为计算长度，L0为设计长度。

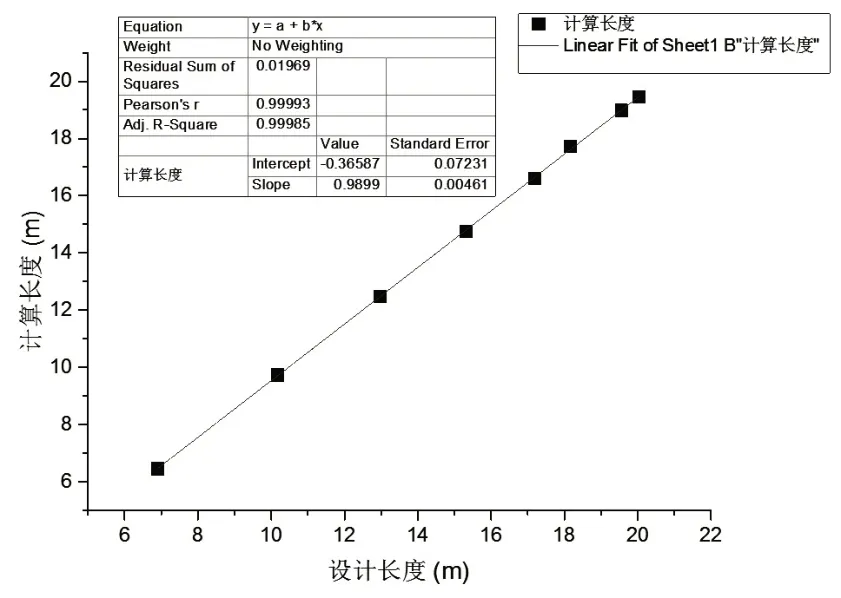
图3 吊杆计算长度拟合

4.3 抗弯刚度对吊杆索力测试的影响

4.3.1 衡武大桥索力测试分析

运用基于弦振动理论的频率法对吊杆索力进行测试，将单位索重（16.8kg/m）与修正后的吊杆计算长度代入相应公式即可得出实测索力值[10-12]。全桥吊杆索力张拉设计值为375kN，当每根吊杆用油压千斤顶张拉至与设计值对应的标定油压表读数后，再用频率法测试。本文仅给出可以代表全桥索力特征的左幅2#～9#内侧吊杆的测定结果（表2、表3），测试结果来源于频率法检测软件系统，如图4所示。

图4 左幅吊杆2#～9#的索力测试结果

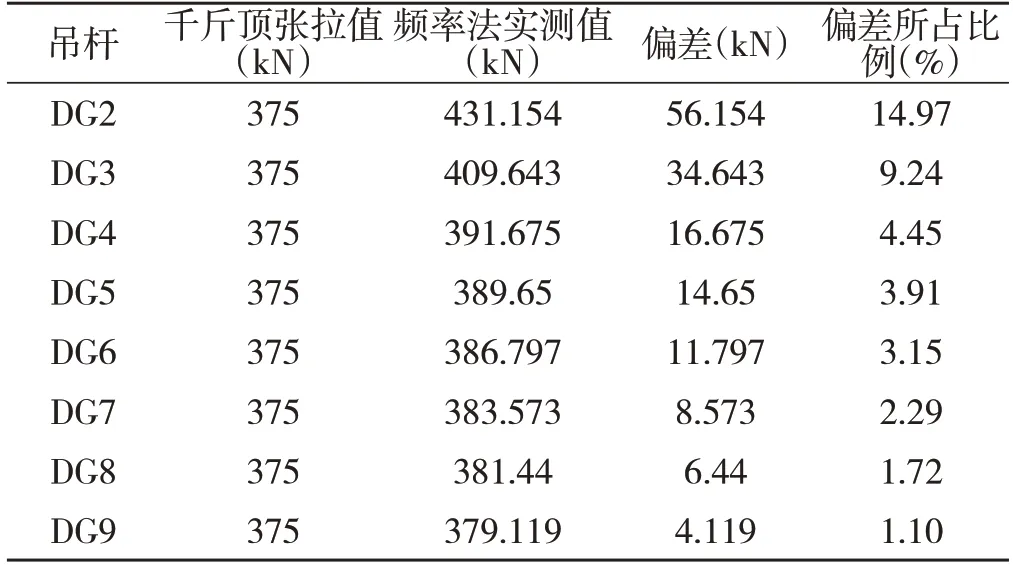
表2 索力测试结果

由上述结果分析得，吊杆2偏差较大，为56.154kN，吊杆3 偏差值为34.643kN，偏差值所占比例分别为14.97%、9.24%，其余吊杆偏差值均在5%以内。由此可知，吊杆长度较短的DG2、DG3 索力实测值受抗弯刚度的影响较大，应在计算索力时将抗弯刚度的影响考虑进来。根据表3 中的数据可知，当考虑抗弯刚度后，各长度的吊杆索力测试值与真实索力值几乎吻合。

表3 考虑抗弯刚度后的索力

4.3.2 不同设计索力值对抗弯刚度的影响

以衡武大桥吊杆参数（表4）为基础，通过选取不同的设计索力值、不同的吊索长度，分析吊杆受抗弯刚度的影响规律（图5），进一步探明不同设计索力值对应的受抗弯刚度影响的索长边界值。

表4 吊杆参数表

图5 不同设计索力值、不同的吊索长度受抗弯刚度的影响规律

由上述分析可知，当设计索力大于2000kN时，所有长度吊索抗弯刚度对索力的影响均在5%以内，可忽略不计；当设计索力值在1000kN～2000kN时，长度小于5m的吊索测试应考虑抗弯刚度的影响；当设计索力值在500kN～1000kN时，长度小于9m的吊索测试应考虑抗弯刚度的影响；当设计索力值在200kN～500kN时，长度小于15m的吊索测试应考虑抗弯刚度的影响。