整体意义关联的教学理解与设计——以“小数的意义”的教学为例

□梅 娅

“小数的意义”在小学阶段的教学中有着非常重要的地位和作用。本文从小数意义的本源性出发，一方面通过分析小数与整数、小数与分数的关系，理解小数的本质含义；另一方面通过解读学生的困难点，分析小数教学后的后测反馈，设计适合知识意义生长和学生认知需求的教学。

一、整体建构意义的需要

（一）小数意义知识建构的需要

1.小数依分数而来

有限小数是由“十等分”分割产生的。百分之一的分量可从十分之一的分量再十等分产生，而千分之一的分量可从百分之一的分量再十等分产生……因此，十等分的活动可任意无限制继续下去。无限被分割的观念正可用来说明小数稠密性的性质，也就是说任意两个小数之间有无限多个小数存在。[1]为此，我们不难发现，计数单位是构造小数数位可迁移的关键点。如果把抽象的计数单位构造，放置在分数和整数十进制的大背景下，借助数线模型或面积模型，就能很好地沟通十进分数与小数之间的联系。

2.小数顺整数而行

学习小数来自两种需要：一是分数书写形式优化改进的需要，二是十进制计数法扩展完善的需要。无论是从数系发展的角度，还是从生活需要的角度而言，小数与整数的关系都是密不可分的。

通过将整数计数单位个、十、百、千……与小数相邻计数单位之间的关系进行对比，可以将小数系与自然数系的结构进行关联（如图1）。在建构小数系的同时，将其自然纳入以十进制为核心概念的数系知识结构体系中，与自然数系共同形成更大的具有内在逻辑联系的学科整体知识结构。[2]在数系概念域中理解小数，我们可以看到，小数虽产生在分数的家族中，却是整数家族的宠儿；小数既是十进分数的一种表达形式，又是按整数家族的方式计数、排列数序和运算的。

图1

（二）小数意义结构化的需要

小数依从十进分数而来，教师通常在小数意义教学时让十进分数“孤立”出现，没有在整数、小数、分数之间很好地建立逻辑关系。教师如何在教学中处理好小数意义的关系连接？将小数意义进行整体建构，与学生已有的认知结构中的整数、分数建立联系，是小数意义纳入知识体系的关键。

1.正视十进分数的距离感和孤立感

从分数到小数，学生在学习中觉得是抽象和困难的，因为对分数的认识基于初步认识。学生首先要理解，接着才能理解0.001米。但在初步认识分数时，一般仅停留在分母是一位数的认识上，很少涉及分母是两位或三位数的分数。

在引出十进分数时，通常会采用数形结合的方式，如涂一涂格子图，得到就是0.01，但有怎样的关系又有怎样的关系，这是一些学生的认知“断层”。

后续体会10 个0.001 是0.01 等十进关系是勉强也很孤立的。从表面上看，让学生通过十进分数理解小数的十进关系是可行的，但在实践中，学生对分数的十进关系是陌生和模糊的，迁移到对小数十进计数单位的理解是困难的。

2.正视小数后续学习的割裂化和无助感

从对后续练习以及教师教学小数性质、小数的近似数等的分析来看，在小数意义的教学中，如果只是单一地从十进分数出发建立小数意义，仅仅停留在分数的“部分与整体”的关系上，则在后续学习中，就会有很大的割裂感和无助感。因为小数性质、小数近似数以及小数加减法等，教学的基础是小数的十进位值制。这就需要教师在小数意义的教学中，融入整数的十进关系，迁移整数十进关系与小数十进计数单位之间的关联，沟通十进分数、小数和整数之间的关系，在教学中实现意义网络化建构，促进概念的迁移和内化。

二、有序完善概念认知的需要

小数的形成有两个不可或缺的前提：一是分数概念的完善，二是十进制计数法的使用。在教学实践中，教师往往过多地关注有限小数就是十进分数的另一种表现形式，突出分数“部分与整体”的关系，而忽略了小数同时也是整数十进制计数法扩展的需要。如何帮助学生将小数意义纳入原有认知结构中，理解内涵并构建新的认知结构呢？

（一）概念有序抽象建模的需要

在初步认识小数阶段，可结合学生的生活情境，以购物（元、角、分）、长度单位（米、分米、厘米）等一些十进关系的单位为载体，让学生借助已有的生活经验，感知十分之一和0.1的关系，从而建立十分之几和一位小数之间的联系。

这需要教师适时地将具体的情境进行抽象化、符号化，在已有一位小数的具体认知基础上，建立小数的模型，特别是两位小数的模型建构。

（二）认知渐进抽象完善的需要

学生的认知过程是不断发展、完善的过程。从具体操作到图式的表征，从形的表征到抽象数的对应，这是基于学生认知的概念学习过程。

人教版教材四年级下册“小数的意义”课后练习中设置了让学生说说小数的含义的题目（第38页第9题）。在对学生的后测反馈中，我们发现，对于小数的意义不仅可以借助具体量感从正反两方面来理解，还可以借助各种图形或者算式，从分数“部分与整体”的关系来描述（如图2）。

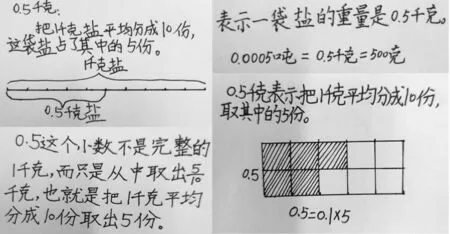
图2 学生后测反馈

小数意义的建构，需要通过抽象渐进式和表征多元化进行。多元表征下的意义理解，是建立在对计数单位的逐个计数和整体构建的基础上的。因为“数（shù）源于数（shǔ），量（liàng）源于量（liáng）”。数概念的教学，包括整数、小数和分数，都可以看作是计数单位累计叠加而来的。数数，是学生自主意义建构的前提。

三、主题呈现课堂探究式材料的需要

对于教学数学概念课，教师要给学生提供对数学模型反复认识、深化理解的机会，并使之具有潜在的可迁移性。主题式的教学素材，通过同类素材的变化整合，凸显概念原型和内涵，有利于概念之间的比较辨析、沟通联系，也有利于举一反三、拓展延伸。在小数的意义的教学中，可充分利用数线模型和面积模型作为课堂主题式材料，在比较中连接整数、联系分数，在迁移中发现、创造小数，在抽象中完善有理数十进制位值制。

（一）借助数线模型，在猜数中沟通比较联系

【教学片段1】猜猜我是谁？

师：我们来玩猜数游戏。猜一猜，这个方框中的数可能会是几？你是怎么想的？

生：我猜是30，只要将0~100 平均分成10 份，100的是10，10是100的。每一份是10，这里大约有3个10，是30。（如图3）

图3

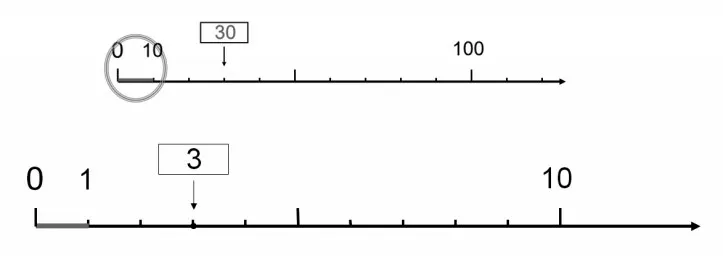
图4

师：如果变成0~10。猜一猜，这个方框中的数要填几？你是怎么想的？（如图4）生：是3，现在将0~10 平均分成10 份，10 的是1，1是10的每一份是1，3个1就是3。

师：这是以“1”为计数单位。想一想，1 与100有怎样的关系呢？

师：那么0~1 之间还有数吗？如果有，这个数会是几呢？（如图5）

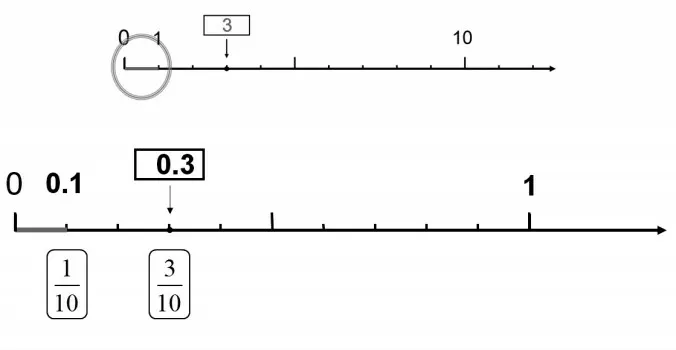
图5

生：有，把0~1 平均分成10 份，每1 份是0.1，3个0.1就是0.3。

师：这1 份是0.1，是怎么来的？这0.3 又是怎么回事呢？同伴讨论。

，

也就是0.3。也可以说是3个0.1是0.3）

为什么都是平均分成10份，得到的3份却是不同的数呢？因为计数单位不同。随着区间不断缩小，当无法精确表示时，需要用更小的计数单位去度量，从而产生小数。在理解小数的意义后可迁移到三位小数、四位小数……

（二）借助多元表征，在数数中促进自主迁移

数的产生是因需要不断扩展而来的，小数概念的形成既是满足现实世界的数量表达的需要，又是数学本身发展的需要。如何在小数意义的教学中，改变原有的教学方式，在数数中数出新的小数呢？

【教学片段2】依次叠加，数出1.2

师：3 个0.1 是0.3，如果继续数，你还能数出哪些数？

生：4 个0.1 是0.4……9 个0.1 是0.9，10 个0.1是1。

生：10个0.1是1.0。

生：1.0 和1 的大小是一样的，都在那个点上。（指数线上的点，如图6）

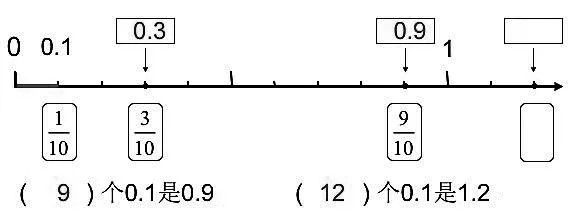
图6

师：那1后面的方框里会是什么数呢？要有理

由说明你的想法是正确的。生：12个0.1是1.2。

生：0.1+0.1+……+0.1=1.2，12个0.1。

生：1+0.2=1.2。

生：我可以以0.1 为计数单位，一个一个往后数，1后面是1.1，1.1后面是1.2。

师：通过刚才的数数，你发现了什么？

生：几个0.1就是几点几。

有限小数是十进分数的表现形式，每相邻两个计数单位之间都是十进关系。通过数线模型上的数数，进一步理解一位小数与0.1、之间的关系。数线的均分和扩充，在数数中对应了小数的扩展，突破了只有纯小数的思维定式，在数线模型上形象化地将小数意义与假分数意义进行对应。学生在教学片段2 中对1.2 的表征是多元的，有乘法意义上的表征、加法算式的表征，还有小数意义文字化的表征，不同的表征都是基于计数单位的数数。

（三）改变学习方式，在表达中激发认知需求

如果说数线模型能满足小数的均分和扩展，那么面积模型则更好地满足形象化的视觉支持。

【教学片段3】精确刻画，画出0.83

变换不同的模型。从1.2数起，按每份0.1依次从大到小减少，当减少到比0.8 多比0.9 少的时候，就产生了对两位小数的认知扩展需求（如图7）。

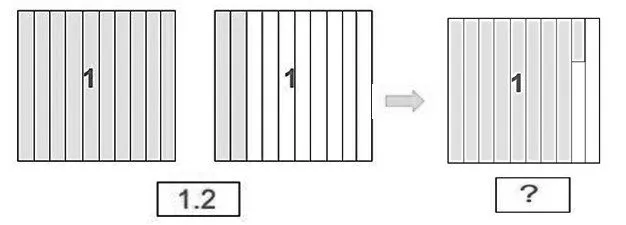
图7

师：用什么数表示图上阴影部分比较合适呢？

生：要分一分才知道这是个什么数。

师：怎么才能分出一个合适的数呢？请你试着分一分，画一画。

（学生独立思考，动手操作，全班交流反馈）生：将0.1 平均分成10 份，0.1 的是0.01，0.01 是0.1 的，每份是0.01，3 个0.01 就是0.03。比0.8多了0.03，0.8+0.03=0.83，就是0.83。

生：8个0.1加3个0.01等于0.83。（如图8）

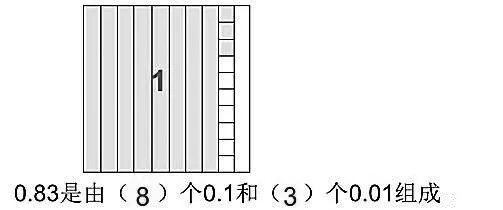
图8

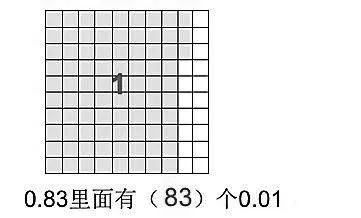
图9

在数数中产生认知冲突，感知当一位小数不能精确表达时，继续十进均分。借助面积、数轴模型十等分再十等分，学生不断感受细分的过程，逐渐体会到两位小数是两个一位小数之间的十进等分，从而将整数“1”的十进均分得到一位小数，迁移到将一位小数“0.1”十进均分得到两位小数，借助面积图，沟通整数与两位小数、一位小数与两位小数之间的本质联系，迁移联想三位小数和无限小数的十进均分。在分一分、画一画、说一说、数一数等活动中，发现小数产生的本质需求，体验具体到抽象的理解过程，从而刻画和理解小数的稠密性。在这样的学习活动中，学生对于整数、分数自然地进行了联系沟通。[3]

（四）双向充分沟通，扩充整个有理数数系

在课后总结回顾时，从“1”出发，不断地均分10 份，产生0.1、0.01、0.001……帮助学生建立小数部分相应的数概念体系。但这样的认知是孤立的。教师还可以让学生反过来：从“0.001”出发，10 个0.001是0.01、10个0.01是0.1、10个0.1是1、10个1是10、10 个10 是100……进一步感知不管是整数部分，还是小数部分，每相邻两个计数单位之间的进率都是十，从整数数系扩充至有理数数系，从而对后续小数的进一步探究积累认知经验。

概念的学习，其最终目的不是为了记住定义，而是要理解概念的本质。不同的认知过程会形成不同的理解水平，若是单纯教学定义，其认知过程主要是模仿、记忆、强化，只能达成“工具性理解”；若突出数学知识之间的本质联系，其认知过程则重在经历、感知、体验，就会形成“关系性理解”[4]。在学生的数学认知结构中，各种数学知识不是孤立存在的，而是有着紧密联系的网络结构，这样的知识网络的构建，有利于学生将新知纳入到原有认知结构中，并形成自己的知识体系。