面向透明工作面的地质建模插值误差分析

安 林，韩保山，李 鹏,2，代振华,3，王新苗

(1.中煤科工集团西安研究院有限公司，陕西 西安 710077；2.西安科技大学 地质与环境学院，陕西 西安 710054；3.煤炭科学研究总院，北京 100013)

煤矿智能化、少人化是实现煤矿安全的重要途径之一。目前，煤矿智能化建设的新高潮正在全国兴起[1-2]。煤矿智能化经历可视远程干预、工作面自动找直、基于透明工作面智能割煤、全智能化自适应开采4 个阶段[3-4]，目前正处于透明工作面智能割煤技术关键阶段。透明工作面智能割煤技术通过三维地震、井巷和钻孔测量等探测手段获取工作面的实际展布情况，在分析上述数据后，利用不同的插值算法建立工作面模型，进而指导采煤机开采工作[5]。在三维地质建模过程中，采样数据是工作面建模的基础，插值是工作面模型实现的必经途径。采样数据量的大小和插值算法在不同程度上影响工作面模型的精确度，定量研究工作面模型精确度影响因素将对插值算法优选和采样数据获取量提供重要的参考价值。

空间插值是一种通过这些离散的空间采样数据计算未知空间数据的方法[6-7]，目前常用的空间插值方法有函数插值[8]、克里金插值[9-11]和光滑离散插值(Discrete Smooth Interpolation，DSI)。由于地质信息的不确定性，函数插值算法在地学模拟上鲜有应用。而克里金算法较为符合地学规律，因此，目前运用于地学建模软件的插值多以克里金插值算法为主。DSI 插值算法[12-13]是依赖于网格节点的拓扑关系，不以空间坐标为参数，是一个无维数的插值方法，能够很好地解决逆断层、陷落柱等多Z(同一位置具有多个Z值)的插值问题，但实现难度较大，鲜有应用。目前，行业内对于地质模型精确性主要集中在插值算法对模型精确度的影响研究[13-14]，因而存在着数据量越大模型越精确的共识，但鲜有人定量研究数据量对于模型精度的影响。

笔者在收集工作面探测资料的基础上，通过交叉验证的方法，计算函数插值、DSI 插值、克里金插值平均绝对误差和均方根误差，对比分析不同插值算法对模型精度的影响。为分析数据量大小对模型精度的影响，提出了相对间距误差。通过计算1%～90%数据量的相对间距误差，得到数据量大小与相对间距误差之间的关系，从而为不同网格间距下最低采样数据量提供参考。

1 智能工作面建模

1.1 建模数据来源及流程

透明工作面建模[15-16]主要包括3 个部分：实测数据获取、地质资料分析、地质模型建立。首先，通过巷道实测、地面钻孔、本煤层钻孔、孔中雷达、三维地震、槽波探测等方法获取实测数据。然后根据工作面的沉积条件、构造起伏等地质条件分析工作面内是否存在地质异常。最后在实测数据导入和地质分析的基础上，通过插值计算，建立工作面透明模型。

1.2 建模插值算法

1) 函数插值算法

函数插值的基本原理是：假定区间[a,b]上的实值函数f(x) 在该区间上n+1 个互不相同点x0,x1,···,xn处的值是f(x0),f(x1),···,f(xn)，要求估算f(x)在[a,b]中某点x*的值。基本思路是：找到一个函数P(x)，在x0,x1,···,xn的节点上与f(x)函数值相同(有时，甚至一阶导数值也相同)，用P(x*)的值作为函数f(x*)的近似。比如反距离加权(Inverse Distance Weighted，IDW) 插值法[17]、趋势面法[18]、样条函数法[19]等。

2) 克里金插值算法

克里金插值算法也称为空间自协方差最佳插值法，它是以南非矿业工程师D.G.Krige[20]的名字命名的一种最优内插法，以变异函数理论和结构分析为基础，适用于区域化变量存在空间相关性。假设存在空间相关性且所有随机误差都具有二阶平稳性。其表达式为：

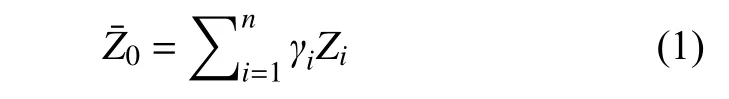
3) DSI 插值算法

DSI 插值算法是法国南锡大学J.L.Mallet 教授[12-13]提出的。通过对一个离散化的自然体模型，建立相互之间联络的网络，如果网络上的点的值满足某种约束条件，则未知结点的值可以通过解一个线性方程组得到。该方法依赖于网格节点间的拓扑关系，不以空间坐标为参数，是一个无维数的插值方法。

针对网格节点上φ值的估计问题，DSI 插值算法建立了计算网格节点φ最优解目标函数：

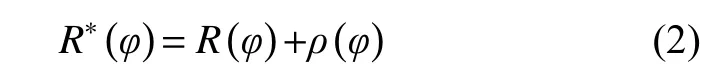
式中：R(φ)为 全局粗糙度函数，ρ(φ)为线性约束违反度函数。

为使目标函数R*(φ)达到最小，需要达到以下2 个条件：(1) 使全局粗糙度函数R(φ)达到最小，从而尽可能使在任意节点上的函数值逼近该点邻域内节点的均值，即使每个节点的φ值尽可能平滑。(2) 将原始采样数据转化成定义在一些节点上的线性约束，使线性约束的违反度ρ(φ)达到最小，即使线性约束符合程度达到最大，从而使相关节点的φ值尽可能逼近采样数据。

2 误差分析方法

本次研究通过采用交叉验证[20]的方法来评价插值方法的优劣。该方法首先假设某些值未知，用周围站点的实测数据通过空间插值来估算该待估点的值，轮流变换待估点，如此反复之后，得出与实测值一一对应的值。将实测值和预测值的均方根误差(ERMS)、平均绝对误差(EMA)作为结果的检验标准[21-22]，EMA可以估算预测值可能的误差范围，ERMS可以反映利用样点数据的估值灵敏度和极值效应。因此，通过计算平均绝对误差和均方根误差，可为基于模型精度的插值算法优选提供参考。

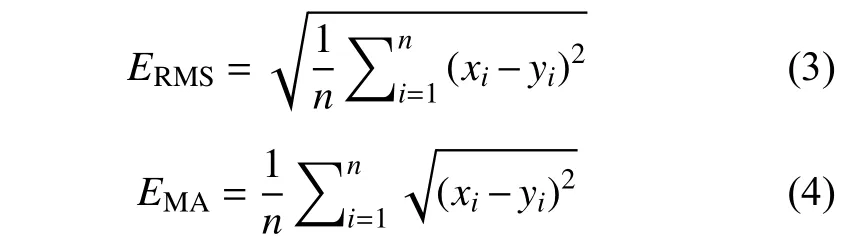
式中：ERMS为均方根误差，EMA为平均绝对误差，xi为第i个点的预测值，yi为第i个点的实测值，n为检验点的个数。

工作面模型要求精度较高，网格大小要求厘米级甚至毫米级。在这种情况下，对网格上全部点进行采样，进而分析数据量的大小对插值误差的影响是不切实际的。因此，本文利用卫星高程数据模拟地层高程进行等间距取样，以此研究数据量的大小对于模型精度的影响。

为了消除卫星高程数据采样密度大(通常为120、90、30 m)与实际工作面间距不匹配，难以用绝对平均误差和均方根误差评价模型误差大小。因此，本文提出相对间距误差(EWA)，作为评价模型精确度的方法，用于表明在同等间距条件下，不同数据量大小对模型精度的影响。并且可以通过相对间距误差计算工作面采样密度下的模型误差大小，以此为采样数据密度和采样数据量提供参考。

式中：L为网格间距。

3 误差分析

3.1 插值算法

利用全站仪获取某工作面的平面坐标和高程，工作面长度为800 m，每隔20 m 获取1 个点，全站仪测量误差为0.001 m，平均高程为838.326 m，最小高程为826.893 m，最大高程为849.142 m，共81 个数据点。

对这81 个点按顺序进行编号，依次抽取3、11、19、27、35、43、51、59、67、75 号点，将剩余的71 个高程点分别作为10 个数据组。这10 组数据利用函数插值、克里金插值和DSI 插值3 种插值算法计算得到抽出点的高程值，将3 种插值算法计算得到的估计值与实际值进行对比。

其中，函数插值和克里金插值由surfer 软件计算生成。克里金插值方法选用的是简单克里金插值，默认插值参数；函数插值选用的插值方法是多项式插值(Polynomial Regression)，参数设置选用三次曲面(Cubic Surface)；DSI 插值使用自编的Matlab 程序，设置各点权函数值为1。通过3 种插值算法得到各点估计值，计算结果对比如图1 所示。

从图1 可以发现，通过3 种插值算法得到的估计值与实际值相差较小，这是由于采样距离间距小，煤层起伏变化不大。为进一步分析3 种插值算法对模型精确度的影响，按照式(3)、式(4)分别计算3 种不同插值算法的平均绝对误差和均方根误差，结果见表1。

图1 不同插值算法计算结果对比Fig.1 Comparison of interpolation results of different methods

通过分析表1，可以得到：DSI 插值的平均绝对误差EMA、均方根误差ERMS值要小于函数插值和克里金插值，因此，DSI 插值算法的可靠性最好，获得的插值曲线更光滑，与地层的实际情况更加相符。

表1 不同插值算法误差计算结果Table 1 Error calculation results of different interpolation algorithms 单位：m

3.2 数据量大小误差分析

获取未经插值某地卫星高程原始数据，数据采样密度为90 m×90 m，共206 080 个数据高程点。将上述高程数据进行均匀采样，获取采样比例分别为1%、2%、3%、4%、5%、6%、7%、8%、9%、10%、40%、70%、90%的13 组数据。由于克里金插值算法相对DSI 插值算法更加成熟，计算量更大，而两者误差比较接近。因此，将13 组数据分别进行克里金插值计算，得到与原始数据量同等大小的估算数据。

为进一步分析数据量对模型精度的影响，按照式(5)分别计算不同采样比例下的EWA值，得到不同采样数据量的相对间距误差分析图，如图2 所示。

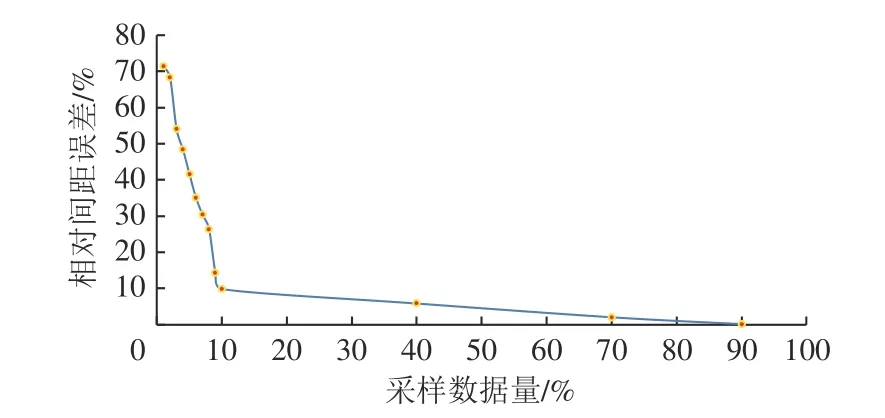
图2 不同采样数据量的相对间距误差分析Fig.2 Analysis of relative spacing error of different sample data volume

由图2 和式(5)分析可知：

(1) 随着采样数据量的增加，模型的相对间距误差逐渐减小。当采样数据量为1%时，相对间距误差在60%以上；当采样数据量大于30%时，相对间距误差降至10%以下。而且当采样数据量大小为1%时，如果模型网格密度为1 m，模型的误差大于0.6 m。因此，可以看出采样数据量对插值误差的影响很大。

(2) 当采样数据量小于10%时，相对间距误差下降幅度很大；但当采样数据量大于10%时，其下降幅度趋于平缓，因此，建议在构建工作面模型时选取数据量大于10%。

4 实例应用

在透明工作面实际构建过程中，工作面模型精度对透明工作面效果具有重要的影响。插值算法和数据量大小是工作面模型精度2 个重要因素。因此，建议在透明工作面构建过程中，一方面，宜采用DSI 插值算法；另一方面，需要提高工作面数据量，为高精度模型提供数据支撑。

插值算法的选用容易实现，如何提高工作面数据量实现较为困难。根据相对间距误差分析可知，对于300 m×1 000 m 的工作面，如果模型误差要求为0.1 m，假设网格密度为1 m，所需数据量大于10%，则要选取采样点大于30 000 个采样点。而目前工作面两巷的数据按照10 m 一个测量点计算，两巷与切眼的测量数据总共为230 个点，相对于能够达到目标精度所需的采样点数量，目前已有数据量低于1%，达不到目标精度所需数据量。

因此，在构建地质模型过程中，必须要对模型进行局部动态更新，提高模型局部数据量，以此提高模型精度。随着工作面不断回采，不断采集切眼处的数据，从而使工作面局部数据量得到增加，局部区域达到目标所需的数据量。如图3 所示，a 区域的单位面积内数据量大于b 区域单位面积内的数据量，因此，插值后a区域的模型精度大于b 区域的模型精度。即切眼处的数据量大于工作面内部的数据量。为保证模型的精度，可以在回采过程中，不断地补充切眼的数据，提高局部数据量，对模型进行更新。

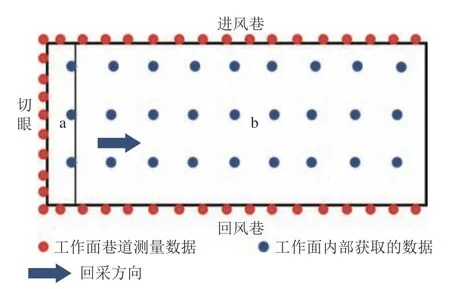
图3 工作面地质模型采样数据Fig.3 Schematic diagram of the sampling data of the working surface geological model

在构建地质模型过程中，为了采样数据量大于10%，可以根据工作面长、宽，计算得到最佳更新距离和切眼数据采样间距。例如，对300 m 宽的工作面(模型误差要求为0.1 m，假设网格密度为10 m)，距离切眼50 m 范围内，数据总量为180 个点，采样数据大于10%，即采样数据大于18 个点，两巷具有12 个数据点，因此，在切眼采样数应大于6 个，切眼采样间距应小于50 m 进行采样。

5 结 论

a.根据交叉验证法，对比分析克里金插值算法、函数插值算法、DSI 插值算法的平均绝对误差、均方根误差，得到3 种插值算法的稳定性：DSI 插值算法的可靠性最好、克里金插值算法次之，函数差值算法最差。

b.采用提出的相对间距误差，分析采样数据量对模型精度的影响，研究发现：采样数据量对插值误差的影响较大；建议在构建工作面模型时，采样数据量大于总数据量的10%。这解决了透明工作面建模采样量大的问题，满足了透明工作面建模高精度要求。

c.在实际构建地质模型过程中，宜采用DSI 插值算法作为透明工作面的插值算法。同时，为了采样数据量大于总数据量的10%，可根据工作面长、宽，采样数据量分析得到最佳更新距离和切眼数据采样间距，提高工作面的局部数据量，对模型进行更新，提高模型精度。