煤层水力压裂应力与裂隙演化的细观规律

2022-07-01李全贵邓羿泽胡千庭张跃兵宋明洋刘继川石佳林

煤田地质与勘探 2022年6期

李全贵，邓羿泽，胡千庭，张跃兵，宋明洋，刘继川，石佳林

(1.重庆大学煤矿灾害动力学与控制国家重点实验室，重庆 400044；2.重庆大学资源与安全学院，重庆 400044)

煤炭资源开采过程中，水力压裂技术作为煤层强化增透的一种技术手段，在一定程度上能提高煤层的透气性，降低瓦斯抽采达标时间，提高抽采浓度，弱化煤层顶底板强度[1-3]。在压裂工程实践中，利用缝槽或导向孔控制裂隙扩展方向，形成压裂缝网，可实现压裂区域的整体增透[4]。然而，裂隙的扩展方向除了受原始地应力及缝槽的影响，也会因煤层物性参数、压裂工艺方法的差异表现出不同的压裂效果，对后续煤层开采产生影响。因此，开展水力压裂应力演化特征及裂隙形态的研究尤为重要，对提高水力压裂技术的科学性，评估压裂效果有重要意义[5]。

前人在理论方面开展压裂增透效果的影响因素研究。程玉刚[6]探究了水力割缝对水力压裂裂隙导向起裂扩展的导向机理，白雪元等[7]建立了拉格朗日元与离散元耦合的连续-非连续数值解法，其计算出的定向射孔水力压裂结果对比GKD 模型理论解有较高的正确性，董卓等[8]依托ANAYS 软件，探究了材料泊松比、注水压力对裂纹偏转角及裂纹扩展路径的影响，得出上述参数的拟合公式及相关系数。Wang Tao[9]、刘顺[10]等通过对水力裂缝与天然裂缝在不同倾角、间距、应力条件下的交错延伸规律进行量化模拟，优化了水力裂缝与非连续天然裂缝网络的交互模型。在物理实验研究方面，Ge Zhaolong[11]、ChengYugang[12]等通过实验室真三轴实验，研究人工预置缝槽对水力裂缝扩展的作用，为煤矿井下体积压裂提供了新的技术手段。吴拥政等[13]对煤矿井下砂岩进行大尺寸原位取样，得出原生层理方向与水平应力差影响起裂压力及压裂曲线，这为煤矿顶板压裂参数设计提供参考。贾奇锋等[14]以不同煤体结构煤为研究对象，重点研究了水力裂缝与天然裂隙交互问题，得出不同煤体结构煤的水力裂缝延伸规律，为裂隙发育下的抽采孔布置提供了依据。

前人的研究着重于水力压裂中不同因素对裂缝最终扩展形态的影响，对压裂过程中裂隙与应力演化规律的分析较少。笔者采用离散元数值方法，以导向压裂为背景，采用应力路径、裂缝热点图等分析手段，对压裂过程进行细观分析，考察不同压裂排量、泊松比、天然裂隙密度等条件下水力压裂裂隙扩展过程中应力与裂隙的细观演化规律，以期为水力压裂范围监测提供支撑。

1 数值模型的构建

1.1 细观参数的确定

基于离散元的颗粒流程序(Particle Flow Code，PFC)对煤体破裂等非连续介质力学问题能更加直观地体现[15]。模型中介质通过刚性颗粒模拟，颗粒之间使用平行黏结模型进行固定，该模型能传递力和力矩，适合模拟煤岩类材料[16]。

煤层的宏观力学参数选自文献[17] 中使用的煤层数据，该煤层平均厚度6.23 m，密度1.28 g/cm3，单轴抗压强度32.22 MPa，抗拉强度2.83 MPa，弹性模量均值1.81 GPa。由于细观参数与宏观参数没有良好的对应性，本文采用试错法[18]对单轴压缩及巴西劈裂数值模拟实验进行参数标定。

单轴压缩模拟试样尺寸为50 mm×100 mm，颗粒数量为8 838；巴西劈裂模拟试样直径为50 mm，颗粒数量为3 419。标定结果如图1、图2 所示，宏观参数见表1，细观参数具体数值见表2，图中红色线段表示加载过程中试样产生的裂隙。

表2 模型细观参数Table 2 Model mesoscopic parameters

图1 单轴压缩标定结果Fig.1 Calibration results of uniaxial compression

图2 巴西劈裂标定结果Fig.2 Calibration results of Brazilian split

表1 试样宏观参数与模型宏观参数的比较Table 1 Comparison between sample macro parameters and model macro parameters

D.O.Potyondy 等[19]指出，平行黏结模型表现出的强度仅与单轴压缩实验相匹配，在模拟巴西劈裂实验时，拉伸强度会过高，与实际值相差较大，但本文标定过程将抗拉强度误差控制在5%以内，标定结果基本符合要求。

1.2 流固耦合的实现方式

在模型中煤体通过圆形颗粒进行表征，为了表达流体与基质之间的耦合关系，引入管域模型[20]。将模型中颗粒之间构成的空间视为“域”，用于存储流体，如图3a 中红色线段围成的多边形；颗粒和颗粒之间存在一个供“域”之间进行流体交换的“管道”，如图3b所示。该“管道”的流量q由微观渗透性系数k、开度a、2 个“域”之间的压差Δp和管道长度L共同决定，遵循Hagen-Poiseuille 方程：

图3 管域模型Fig.3 Pipe-domain model

由上式可以看出，开度a会影响通过流体管道的流量大小，即模型的渗透性。而开度a的大小由颗粒之间的接触状态决定，假设存在一个初始开度a0，当颗粒之间为拉应力时：

当颗粒之间为压应力时：

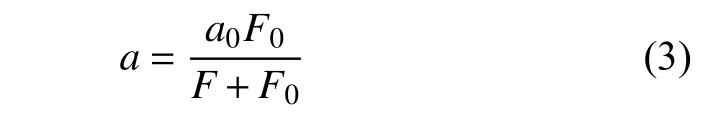
式中：λ为缩放因子；d为两颗粒之间的距离，m；R1、R2为颗粒半径，m；F0为管道开度降为初始开度一半时的法向力，N；F为颗粒当前接触力，N。

模拟的水力压裂过程是以时间步进行的，在一个Δt时间步内，由于流域之间流体交换导致的流域压力变化主要受流体体积压缩模量的影响。假设某个流域有N条流体管道与之连接，则在一个时间步内，流域内的压力变化[21]为：

式中：Kf为流体的体积模量，Pa；Vd为流域体积，m3；ΔVd为流域体积的变化量，m3。

流域内的水压也会对周围的颗粒产生体积力，并作用在颗粒表面，如图3c 所示。则颗粒受到的合力为：

式中：p为域内压强，Pa；ni为域中心指向球心的单位矢量；D为颗粒直径，m。

模型整个耦合过程主要体现为以下3 点：颗粒之间接触状态的变化影响着流体通道的过水能力，从而影响局部材料渗透率；流体在流域之间的交换引起流域之间的压力变化；流域压力会对周围颗粒产生推移作用。

在整个过程中，交替使用前文的流动方程和压力方程来实现水力压裂现象。为了使模型稳定运行，需要保证域内的压力变化小于扰动压力，当两者相等时可以求出临界时间步长[22]：

式中：N为流域所连接的管道数；r为流域周围颗粒的平均半径，m；α为小于1 的安全系数。

为了保证在压裂过程中水压能有效地传递，规定产生的裂缝若由水压导致，则该裂缝对应的2 个流域内的液体压强等于2 个域压力值中的较大值，在保证模型稳定的同时提高了计算效率[23]。

2 模拟方案设计

本文采用PFC2D软件建立了200 mm×200 mm 的二维离散元模型，模型正中心设置半径为7 mm 的压裂孔，并在与X轴方向夹角45°的位置预置了长度为3.5 mm 的导向槽模拟导向压裂过程[24-25]。依据文献[26]，该煤样所在矿区煤层平均埋深760 m，最大水平主应力为最小水平主应力的1.82 倍，故在模型X轴施加7.28 MPa 载荷，Y轴施加4.00 MPa 载荷模拟煤样所处的实际地应力。为了描述压裂孔附近的应力演化状态，应力监测区域共设置3 个，使用测量圆进行监测，距离右侧边界50 mm，均匀垂向布置，用于绘制整个压裂过程中不同区域的应力路径曲线，如图4 所示。

模型的四周为透水边界，所有颗粒的运动遵循牛顿第二定律与力-位移定律。模型中采用光滑节理模型来模拟天然裂隙处的力学性质，天然裂隙的长度及角度分布服从幂律分布，统计通过固定参考线的裂隙数量控制天然裂隙的密度。

在现有的研究中，压裂排量、泊松比、天然裂隙密度等因素作为水力压裂研究的热点，它们的改变之所以导致压裂结果不尽相同，是因为这些因素的存在改变了压裂孔周围的应力分布状态，使局部应力发生了重新分布。因此，模拟方案包括以上3 个因素，每个因素3 个水平，除去1 组重复实验，共8 组，模拟压裂时间均为140 s。具体模拟实验方案见表3。

表3 水力压裂模拟方案设计Table 3 Scheme design of hydraulic fracturing simulation

3 结果分析及讨论

通过绘制压裂过程中的裂纹热点图及监测区域的应力路径，分析不同影响因素下水力压裂区域应力与裂隙细观演化规律。

在裂隙表征方面，由于离散元模型精度的原因及颗粒的不连续性，宏观裂隙的扩展方向并不能由微裂隙的扩展方向直接表示，而是通过微裂隙在一个时间段内各个方向上的分布比重体现的，如图5、图6d 所示。裂隙热点图可表明压裂过程中每隔4 s 各个角度范围内的裂隙扩展数量，灰色虚线为比重参考线，代表每个时间间隔内角度的平均值，均值处于90°表明宏观裂隙沿原有方向扩展。在应力表征方面，应力路径能描述某一区域及其附近局部主应力的变化情况，通过统计不同时间点每个监测区域的最大主应力，并将其按时间顺序连接成线得到；根据最大周向拉应力准则，一定程度上可用于判断该区域在压裂过程中裂隙在每个时间点扩展方向的可能性及附近裂隙尖端的应力状态[26]，黄色虚线(图6g、图6h、图6i)为恒定应力比参考线，代表σ2/σ1的比值。

图5 微裂隙扩展形态Fig.5 Schematic diagram of microcrack propagation

3.1 不同排量下水力压裂应力与裂隙细观演化规律

图6 为不同排量下水力压裂裂隙分布、裂隙热点及应力路径对比。当煤体物性参数一致时(方案设计1、2、3 号实验)，如图6a—图6c 所示，压裂排量越大，压裂半径越大；压裂平均半径从20 mL/min 条件下的26 mm 增加到了60 mL/min 条件下的58 mm，增加为原来的2.2 倍。从图6d—图6f 中可以看出，压裂排量越大，裂隙产生的时间越早，即起裂时间越短，且高排量情况下，裂隙扩展的大事件数量及有信号的时间段都有较大增加。当压裂排量为60 mL/min 时，出现了裂隙的二次扩展现象，在90～130 s 时出现了裂隙扩展的空白期；可能原因是较高压裂排量导致了裂隙的快速扩展，而在裂隙扩展后由于裂隙容水体积迅速增加，导致水压下降明显，不足以让裂隙尖端产生足够的应力条件使裂隙继续扩展，致使裂隙扩展暂时停滞。3 种排量下，虽然起裂初期微裂隙角度均值偏离90°较大，但产生的裂隙数量较少，对裂隙原有的扩展方向影响程度不明显；起裂经过20 s 后，微裂隙均值主要分布在90°～120°范围内，随着微裂隙数量的逐渐增加，宏观裂隙扩展方向由45°向90°推进，偏转程度逐渐增加。

图6 不同排量下水力压裂应力与裂隙细观演化特征Fig.6 Mesoscopic evolution of hydraulic fracturing stress and fracture at different flow rates

应力演化方面，如图6g—图6i 所示，由于压裂孔和导向槽的存在，3 个区域内的初始地应力状态均有一定程度的偏移，其中2 号区域偏移程度最大，均向着低局部应力比值的方向发展。20 mL/min 和40 mL/min排量下，压裂过程中3 个测量区域内的应力演化方向及最终应力路径曲线形状较为相似，而在60 mL/min排量下，上述特征会有明显的改变。在压裂排量为20 mL/min 和40 mL/min 时，1 号区域和2 号区域的局部主应力向着更高应力比的方向发展，且2 号区域σ2/σ1的增加更为明显。随着1 号区域和2 号区域σ2/σ1的增加，裂隙扩展逐渐偏向X轴方向。而3 号区域的σ2/σ1值在1.5～2.0 的范围内波动，其数值与原始地应力状态比值大致相同，但数值在压裂过程中不断增大，应力集中现象较为明显。说明随着压裂的进行，裂隙尖端附近的应力比值在不断增大，使得裂隙的后续扩展受局部地应力的影响逐渐增加，从而偏离原有的扩展方向。在压裂排量为60 mL/min 时，1 号区域与3 号区域应力演化方向类似，且σ2/σ1相较原始比值变化不大；而2 号区域σ2/σ1在压裂后期向着比值较小的方向发展，说明随着压裂排量的升高，裂隙沿原有方向的扩展能力也会随之加强，抵抗一部分由于局部地应力作用而产生的裂隙偏转现象，与图6c 所示结果相对应。

3.2 不同泊松比下水力压裂应力与裂隙细观演化规律

当压裂排量为40 mL/min 时(方案设计2、4、5 号实验)，如图7a—图7c 所示，随着试件泊松比的升高，压裂半径急剧降低，压裂平均半径从ν=0.16 条件下的82 mm 减少到了ν=0.35 条件下的16 mm。由图7d—图7f 中可以看出，煤体泊松比的变化对试件的起裂时间影响不明显，3 个试件均在压裂80 s 后起裂，但泊松比会严重影响试件最终的裂隙发育情况及裂隙扩展的大事件数量，因此，具有较高泊松比的煤体更难压裂。

图7 不同泊松比下水力压裂应力与裂隙细观演化特征Fig.7 Mesoscopic evolution of hydraulic fracturing stress and fracture under different Poisson’s ratios

应力演化特征如图7g—图7i 所示，ν=0.16 试件的应力演化趋势表现出与压裂排量为60 mL/min 的情况类似，1 号和3 号区域σ2/σ1保持在1.5～2.0 附近波动，而2 号区域σ2/σ1先升高再降低。ν=0.35 试件的应力演化趋势表现出与压裂排量为20 mL/min 的情况类似，3 号区域σ2/σ1保持在1.5～2.0 附近波动，而1 号和2号区域σ2/σ1一直处于上升趋势。在不含天然裂隙试件的应力演化过程中，除去水压对地应力的扰动作用，只有裂隙扩展对局部地应力的分布会有影响，此处未考虑压裂过程中瓦斯流动及煤体遇水软化造成的孔隙压力变化。结合裂隙分布图可以得出，水力压裂过程中，压裂孔附近的应力演化方向及最终应力路径曲线形状受当前裂隙扩展情况影响显著，而这种裂隙扩展情况无论是压裂排量还是泊松比所导致，并不会影响其与应力路径的对应关系。

3.3 不同天然裂隙密度下水力压裂应力与裂隙细观演化规律

当压裂排量和煤体力学参数一定时(方案设计6、7、8 号实验)，如图8a—图8c 所示，天然裂隙密度越高，水力裂隙的形状越复杂，且裂隙扩展的方向性几乎没有规律可循。可能原因是在较高的天然裂隙密度条件下，如碎裂煤或碎粒煤，供压裂液滤失的通道显著增加，导致新裂隙产生较少，压裂液更多的是对原有天然裂隙的扩展。从图8d—图8f 中可以看出，在相同的压裂条件下，随着天然裂隙密度的升高，起裂时间并没有发生较为明显的改变，均在压裂60 s 后开始起裂；但在60～140 s 裂隙扩展阶段，微裂隙在各个角度上的数量都有显著的降低趋势；且微裂隙角度均值波动程度逐渐增大，没有明显的偏向性。因此，天然裂隙发育程度高的煤体，其水力裂隙走向受天然裂隙影响明显，且多条水力裂隙被天然裂隙捕获，扩展方向受限。

图8 不同天然裂隙密度下水力压裂应力与裂隙细观演化特征Fig.8 Mesoscopic evolution of hydraulic fracturing stress and fracture under different natural fracture density

应力演化特征如图8g—图8i 所示，随着天然裂隙密度的增加，3 个区域应力演化的规律性逐渐减弱，且应力变化幅度逐渐减小；初始地应力状态的偏移程度相较于完整试件更加明显，偏离值上升了一个数量级，偏离范围由0.1～1.0 MPa 增至1.0～5.0 MPa，偏离位置也由于天然裂隙的随机性而无法预测。

天然裂隙密度较低时，如裂隙发育程度较低的原生结构煤，应力演化方向及最终应力路径曲线形状与压裂排量为60 mL/min 的情况类似，3 号区域均在压裂后期由局部高地应力比值向低应力比值方向发展。天然裂隙密度中等时，上述应力特征与压裂排量为20 mL/min 和40 mL/min 的情况类似，1 号区域应力状态整体变化不大，σ2/σ1在1.5～2.0 之间波动；3 号区域σ2/σ1不变但σ1随σ2的增大而增大；2 号区域σ2/σ1在不断增大，由1.6 增加到10.0 以上，该区域裂隙沿X轴扩展的概率随压裂过程逐渐增大。当天然裂隙密度较高时，如碎裂煤，由于天然裂隙的影响，3 个区域内的应力演化特征没有较好的规律性，多个区域出现了应力演化方向的反转现象，应力状态更加随机，难以预测。

因此，高裂隙发育的煤层地应力状态更加复杂，煤层整体地应力状态并不能代表局部应力状态，对于该类煤层的增透方案设计需要因地制宜。

3.4 工程应用模式探讨

研究结果表明，压裂排量的增加导致压裂半径也随之增加，但泊松比较高的煤层水力裂隙很难扩展，这一结论与董卓等[11]的研究结果得到很好地相互印证。因此，针对泊松比较高的煤层，压裂方案设计需要考虑更多的因素；而天然裂隙发育过高的煤层，裂隙的扩展方向几乎无法预测，并且由于压裂液滤失严重，存在无法蹩压的现象，需要更大的压裂排量达到相同的压裂效果。

另一方面，低压裂排量、中天然裂隙密度和高泊松比试件的应力演化方向及最终应力路径曲线形状类似，而高压裂排量、低泊松比和低天然裂隙密度试件的上述应力特征类似，对比其宏观裂隙分布图，可以得出某一区域应力路径的演化特征能够反映出裂隙的扩展状态，并且这种应力演化特征与裂隙扩展状态的对应关系只与当前地应力情况及裂隙扩展情况有关，而与何种因素导致的这种裂隙扩展状态关系不大。因此，该方法为压裂范围的监测提供了一条新的思路：在压裂前期，现场可设置几组应力监测区域记录并评估压裂区的应力路径曲线和缝网扩展情况，在后续压裂施工过程中可将此次应力路径曲线与先前的压裂数据进行对比分析，结合其他压裂范围监测手段如微震、瞬变电磁等，可更加精确地判断该次压裂缝网的扩展范围。但天然裂隙发育的煤层由于应力分布的复杂性，该方法并不适用。