基于多字典联合与分层块稀疏贝叶斯框架的多辐射源直接定位方法

叶泓臻 郭海召 关浩亮 张顺生* 王文钦

①(电子科技大学电子科学技术研究院 成都 611731)

②(中国电子科技集团第五十四研究所 石家庄 050081)

③(电子科技大学信息与通信工程学院 成都 611731)

1 引言

辐射源的精确定位问题在电子侦察、无线通信等领域受到了广泛的关注，例如利用蓝牙设备在复杂且不可预测的室内环境中进行定位[1]。主流的定位方法称作两步法，通常采用两个处理步骤[2,3]，第一步估计到达时间(Time of Arrival,TOA)、到达角(Angle of Arrival,AOA)、接收信号强度(Received Signal Strength,RSS)或多普勒频移等定位参数，第二步使用先前估计的参数来定位辐射源。这些方法具有运算复杂度低，不需要将观测数据汇总处理等优点而广泛应用。但这些方法估计参数时不可避免存在参数估计误差，导致定位精度的下降。另外，两步法还必须将各接收基站估计的定位参数关联才能实现多辐射源定位。为了解决上述问题，Weiss[4]提出了直接定位(Direct Position Determination,DPD)方法，该方法通过联合利用所有基站的观测值以及在感兴趣区域内进行穷举搜索，一次性就能直接估计出所有辐射源的位置。

与信号处理领域的传统数据模型相比，压缩感知(Compressed Sensing,CS)在低信噪比(Signal-to-Noise Ratio,SNR)和少快拍的情况下具有更好的鲁棒性[5]。文献[6]提出了一种使用ℓ1范数的压缩感知方法，但这种方法需要预先确定合适的正则化参数。为了避免这一缺点，基于自适应迭代更新参数的稀疏贝叶斯学习(Sparse Bayesian Learning,SBL)的方法被提出[7,8]。Zhang等人[9,10]提出了一种块稀疏贝叶斯学习(Block Sparse Bayesian Learning,BSBL)的求解方法，该方法引入了信号块内的时间相关性，并且具有速度快、性能好的优点。为了获得相较于传统贝叶斯学习更稀疏的重构性能，Babacan等人[11]提出了利用Laplace先验的分层贝叶斯模型。在文献[12]中，多字典稀疏贝叶斯学习用于联合处理多频率字典下具有共享稀疏性的不同观测信号。最近，基于压缩感知的方法也应用于辐射源定位[13,14]，但它们往往假设信号传播模型特性是完全已知的。然而在实际应用中传播模型并不容易完全获知，不同接收基站接收到的信号会受到信道衰减的影响，导致构建的过完备字典和真实的字典之间存在误差，因此不能直接联合多个接收信号进行处理。为解决上述问题，一种思路是通过学习更新字典的方式来完成多辐射源定位[15,16]，但面临运算量大的挑战。另一种思路是利用辐射源信号在不同字典的共享稀疏性来进行定位[17,18]，其中文献[18]通过对稀疏字典进行重组进一步提升了定位性能，但文献[17,18]的方法需要预先知道辐射源的个数。

本文提出了一种基于多字典联合的SBL方法来解决具有信道衰减的辐射源定位问题。考虑在无源定位的场景下，多个接收基站接收来自同一辐射源的信号，将辐射源定位问题转化为具有共享稀疏性的稀疏信号的恢复问题。在建立基于Laplace先验信息的分层贝叶斯框架基础上，使用了基于多字典的SBL方法重构稀疏信号，估计辐射源的位置。

2 接收信号模型

考虑有N个辐射源，每个辐射源的位置由D×1矢量pn表 示。有L个 具有M个阵元的接收基站截获辐射源发射的信号。则第l个接收基站接收到的信号可以表示为

其中，rl(t) 是一个依赖时间的M×1信号观测向量，βl,n(t)表示从第n个辐射源到第l个接收基站的未知复信道衰减是第l个接收基站对第n个辐射源的阵列响应，其中f是信号的载波频率，d是阵元间距，θl,n为第n个辐射源到第l个接收基站信号入射角度相对于法线方向的夹角，c为电磁波的传播速度。sn(t-τl(pn)) 是第n个辐射源发射的信号延时τl(pn)后 的波形。向量nl(t)为零均值的高斯白噪声并且与辐射源信号不相关。由于信道衰减的幅度和相位会随着传播环境的改变而变化，未知的信道衰减βl,n(t)与时间有关。假设观测时间与相干时间相比足够小，则信道衰减可以认为在相应时间保持不变，即βl,n=βl,n(t)。对式(1)作离散傅里叶变换(Discrete Fourier Transform,DFT)，得到对应于第l个接收基站的接收信号的第k个频率分量表达式为

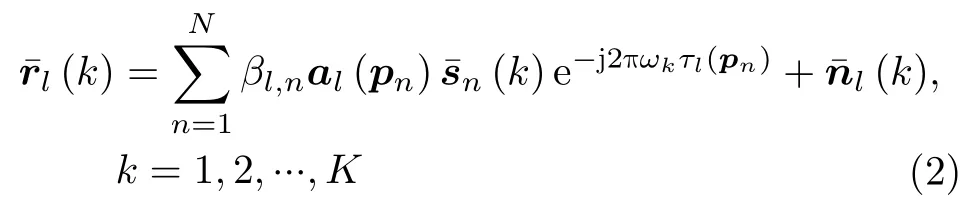
其中，ωk是第k个离散频点的频率分别是rl(t),sn(t),nl(t) 在第k个离散频点的数据是相位延迟，取决于辐射源和接收阵列之间的距离。值得注意的是，信道衰减总是和信号一起出现，影响信号的幅度和相位，从而使信道衰减和信号之间产生模糊。因此，信道衰减可以视作信号的一部分，每个接收基站接收到的发射信号可以认为具有不同幅度相位，但存在比例关系，来自同一位置。并定义，则接收信号在频域上可以重新表示为

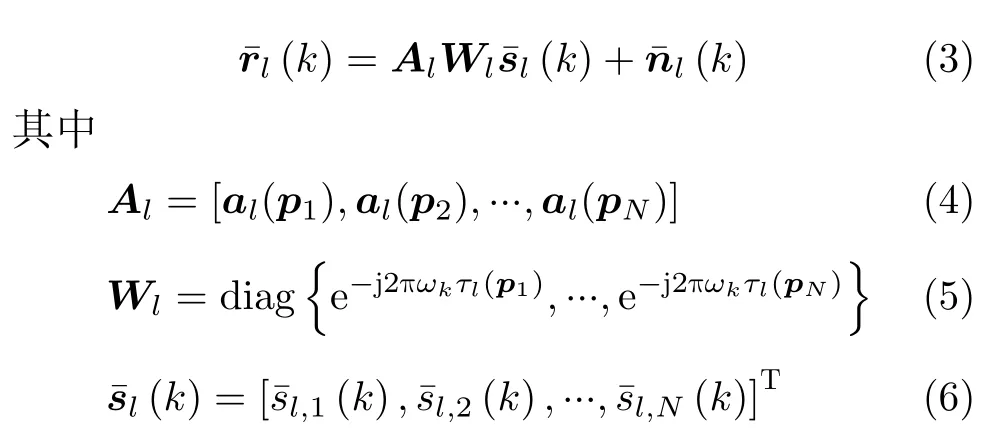
其中，diag{·}代表将元素按矩阵主对角线排列，而辐射源的位置信息被包含在阵列响应Al以及信号的延时τl(pn)中。第3节将使用TOA和AOA信息推导过完备字典矩阵，将信号模型扩展到BSBL框架中。

3 多辐射源直接定位方法

由于字典是部分未知的，不能用单一的字典来恢复信号，所以本文引入了块结构，使得每个接收基站的接收信号可以用一个列向量来表示。另外，每个块的块内相关性在信号中广泛存在，通过探索和利用块内相关性能够提升算法的性能[9]。因此，式(3)可以推广为

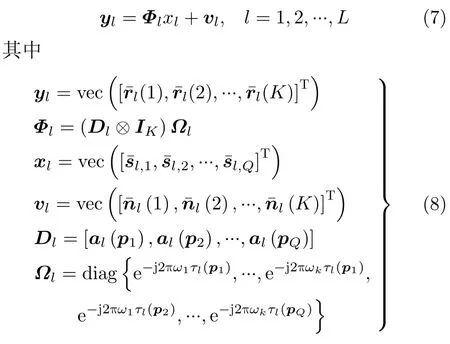
其中，vec(·) 代表将矩阵按列连接成列向量，⊗代表克罗内克积，IK代表大小为K×K的单位矩阵，Q是感兴趣区域的网格数，也是字典中的原子数。为了方便，使用xl,q代替，假设所有的xl,q服从零均值的高斯过程

其中，γq是一个未知的非负超参数用来控制xl的块稀疏性。当γq=0 时，与之相关联的第q个块会变为零。Bq是一个正定矩阵，代表了xl,q块内相关性结(构。当这些块)互不相关时，xl的先验概率为其中Σ0=是一个块对角矩阵。另外，γ=[γ1,γ2,...,γQ]为一个超参 数。并且服从Gamma分布：

其中，Γ (γq|1,ξ/2)=ξ/2·exp(-ξγq/2),ξ ＞0,Γ(·)为Gamma函数。边缘概率密度xl,q为

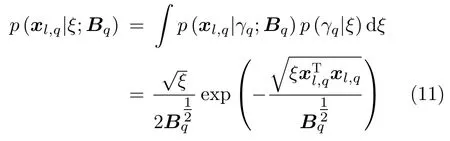
如式(11)所示，边缘概率密度xl,q服从Laplace先验，相较于常规的高斯先验，Laplace分布的概率密度更集中在零附近，更能鼓励稀疏性特征。通过Gamma函数对ξ进行建模有

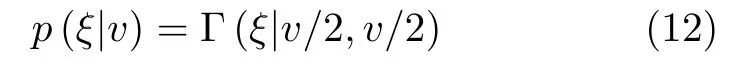
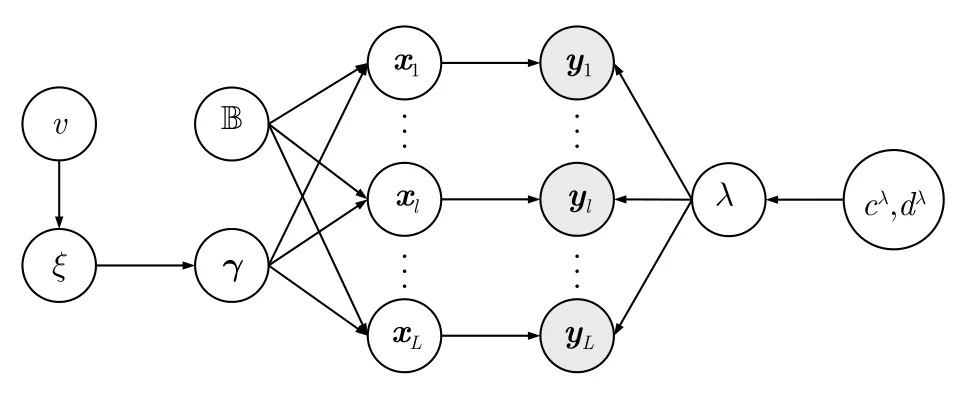
图1 基于Laplace先验的分层块稀疏贝叶斯模型图Fig.1 The figure of hierarchical block sparse Bayesian model based on Laplace prior

xl的后验概率可以写为

尽管式(14)有L个不同的µl,x和Σl,x表达式，但本文认为Σ0和λ在不同表达式中是一样的，因为信道衰减并不改变信号稀疏性和噪声方差，不同观测站的观测数据可以用具有共享稀疏性的不同字典来表示，这种共享稀疏性可用于多字典的联合重建。即认为不同xl中的第q个块的概率密度受同一个参数γq所控制，联合分布可以写为

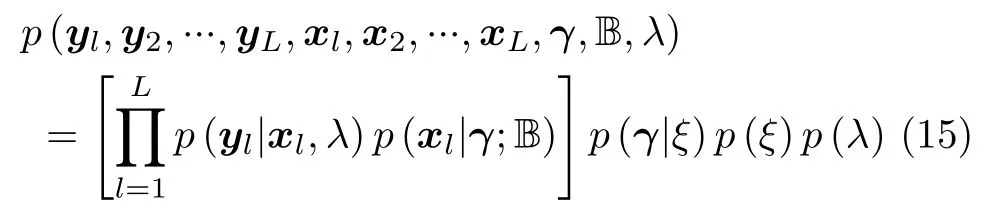
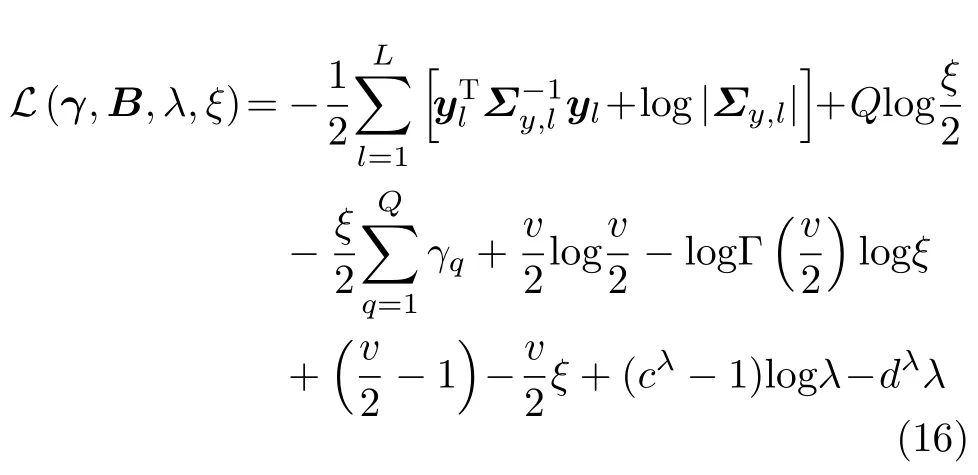
其中，|·|代 表矩阵的行列式并且式(16)中的常数项已被省略。由文献[9]可知，Bq仅影响局部的收敛解而不会影响式(16)的全局最小值，而全局最小值往往会对应真正的稀疏解。不过，对每个块指定一个可能会导致过拟合，因此，这里用Bq的平均值来避免过拟合。因此，Σ0变为Σ0=Γ ⊗B-1，其中。参考Bq经典的稀疏贝叶斯推导过程[8]，式(16)第1项可以写为

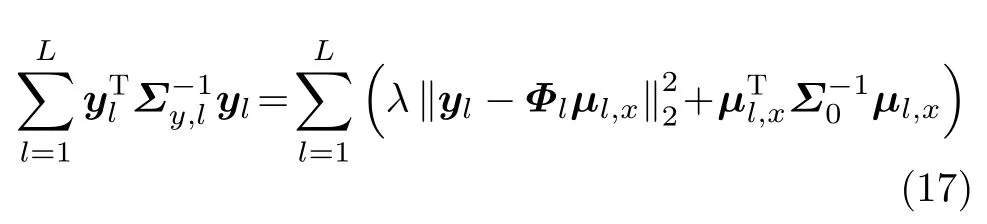
其中，‖·‖2代表向量二范数(或矩阵二范数)。根据BSBL-BO算法[10]，式(16)的第2项有一个上界

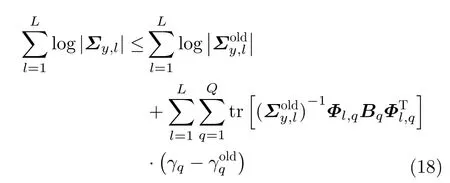
令L(γ)/dγ=0，可得γ1,γ2,...,γQ的估计

其中，上标 (·)*代 表本次更新的参数。类似于对γ的求解，可以估计出其他参数的更新方程

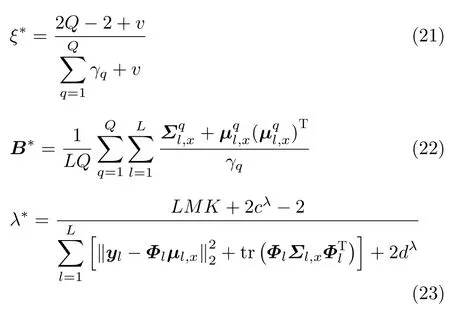
超参数v可以设置为一个常数或者使用式(24)进行参数更新

其中，ψ(v/2)代 表l n Γ(·)函 数在v/2处的导数。

利用得到的所有参数的更新方程，可以通过迭代更新各个参数。迭代求解的步骤为：

步骤1 初始化参数γ为全1的向量，λ-1→0,B=IK,ξ=1,v=1，并将γ的门限设置为1 0-4；

步骤2 根据当前γ,B,λ,ξ,v利用式(14)获得µl,x,Σl,x；

步骤3 利用步骤2获得的均值和方差通过式(20)—式(24)来更新得到新的参数γ,B,λ,ξ,v的估计值；

步骤4 若某个网格点的γq小于所设置的门限，则令该网格的γq=0，不再对该网格进行参数更新；

步骤5 判断算法迭代收敛的条件是否已经满足，如果未满足跳回步骤2；如果条件满足，终止迭代到步骤6；

另外，稀疏贝叶斯理论适用于实数信号的处理，为了使本文推导的参数更新方程适用于复数信号处理，必须将复数形式转化成实数形式来处理[19]。式(7)被修改为

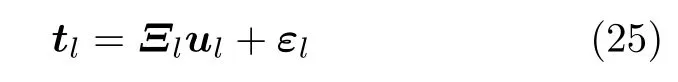
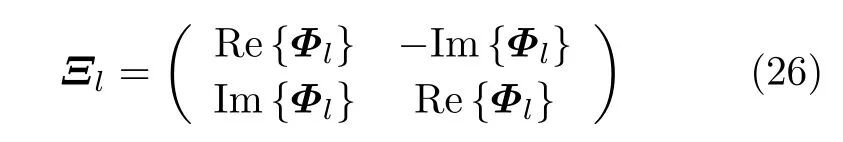
Re{·}代 表取实部操作，I m{·}代表取虚部操作。应用算法恢复出ul后，其实际所对应的复数模型下的xl估计为

4 算法复杂度和收敛性分析

不同定位方法的运行时间对比如表1所示。对比实验中，目标的搜索范围为px ∈(-2,2),py ∈(-2,2)(单位：km)的区域内，以0.2 km为网格间距进行搜索。与算法复杂度相关的其他参数设置为：SNR=20 dB,M=10,K=8,L=4，辐 射 源位置为(100,100)(单位：m)。从表1可以看出：两步法是所有定位方法中运算速度最快的，文献[18]的定位方法由于不需要迭代运算，其计算效率比本文所提方法和BSBL-BO方法都要快。

表1 不同定位方法运行时间对比Tab.1 Comparison of run time

此外，本节推导了未知路径损耗衰减条件下辐射源定位误差的克拉默-拉奥界，作为估计误差的下界。对于定位模型yl=Φlxl+vl,l=1,2,...,L，其均值和方差可表示为

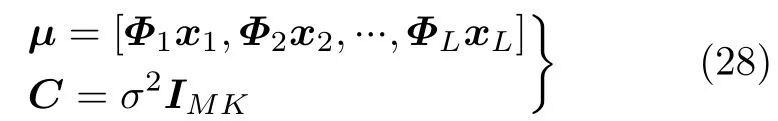
则Fisher信息矩阵可表示为

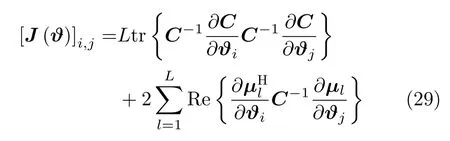
将式(30)代入式(29)，则有

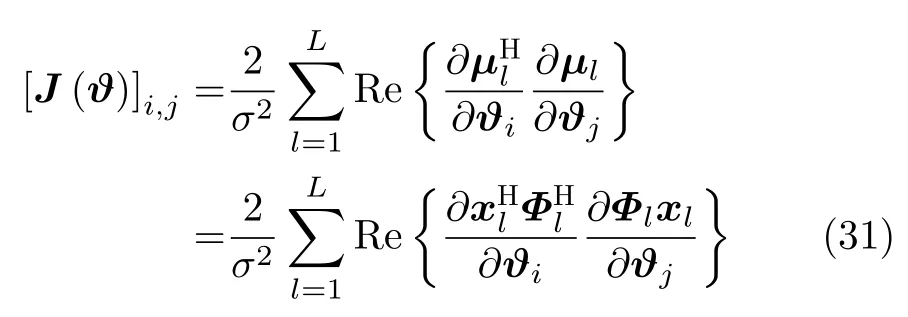
进一步可得

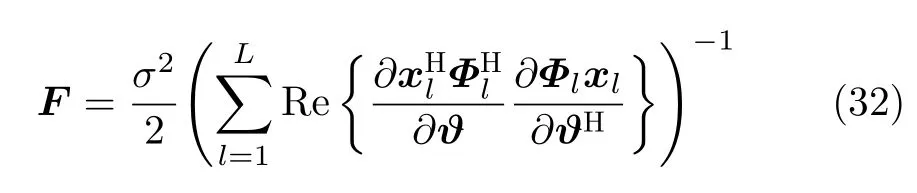
那么，对于辐射源位置的估计pq,q=1,2,...,Q，估计误差的CRLB可表示为

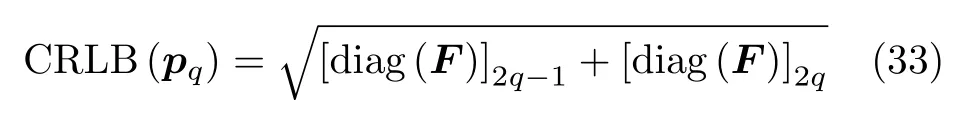
5 仿真分析

本节通过仿真分析基于分层块稀疏贝叶斯算法的辐射源估计性能，为了检验所提出的定位框架的性能，本文假设其中4个接收基站分别位于(–5,–5),(–5,5),(5,–5)和(5,5)(单位：km)。每个站采用一个均匀线性阵列(Uniform Linear Array,ULA)，每个阵列有M=10个阵元，阵元间距设置为d=λc/2，其中λc表示信号波长。将信噪比定义为接收信号的平均功率与噪声功率之比。路径损耗衰减建模为βl,n=1+δl,n，其中δl,n是一个零均值，方差为0.1的复高斯随机变量[4]。

由于本文研究的重点是定位方法的研究，尽管基站的物理位置、分布的几何形状会对定位算法造成相应的影响，其具体影响可参考文献[20]，本实验中仅考虑给定接收站几何分布情况下的辐射源定位。另外，当辐射源不在所预设的网格点上时，基于稀疏贝叶斯的方法会存在一定的离格误差。同样的，尽管离格误差会对定位算法造成相应的影响，但在本文中也忽略其影响，假设辐射源均处在网格点上，具体辐射源离格的定位情况可参阅其他文献[14]。

仿真1：设置S NR=20 dB，快拍数为16，两个辐射源分别位于(0，80)和(50,–50) (单位：m)。假设所有发射信号都是未知的二进制相移键控(Binary Phase Shift Keying,BPSK)调制信号，并且具有相同的带宽1 MHz，载波频率为1 GHz。两个辐射源的定位结果如图2(a)、图2(b)所示。可以看出，图中有两个明显的尖峰，它们代表着算法所获得的辐射源位置的估计，其余的点均因为在参数更新过程中γq小于设定的门限值而被剪枝。从图中可以看出，算法很好地区分这两个相近的辐射源，这验证了算法的有效性。

图2 所提算法对辐射源的定位效果示意图Fig.2 Localization result of emitters using the proposed method

辐射源有3个，分别位于(0,80),(50,–50)和(–60,–70) (单位：m)时，辐射源较多时，稀疏性下降，所提出算法会出现一定的伪峰，稀疏恢复性能会变差，但伪峰总体高度较低，仍能较好地获得辐射源的准确位置。

仿真2：利用均方根误差(Root Mean Square Error,RMSE)来评估所提出方法的性能，其定义为

不同定位方法的RMSE随信噪比的变化关系如图3所示。可以看出：随着信噪比的增大，不同定位方法的RMSE均接近CRLB。当信噪比低于0 dB时，两步法的定位误差明显大于其他直接定位方法。低信噪比条件下，本文所提方法的定位性能优于DPD、文献[19]的方法和BSBL-BO方法。

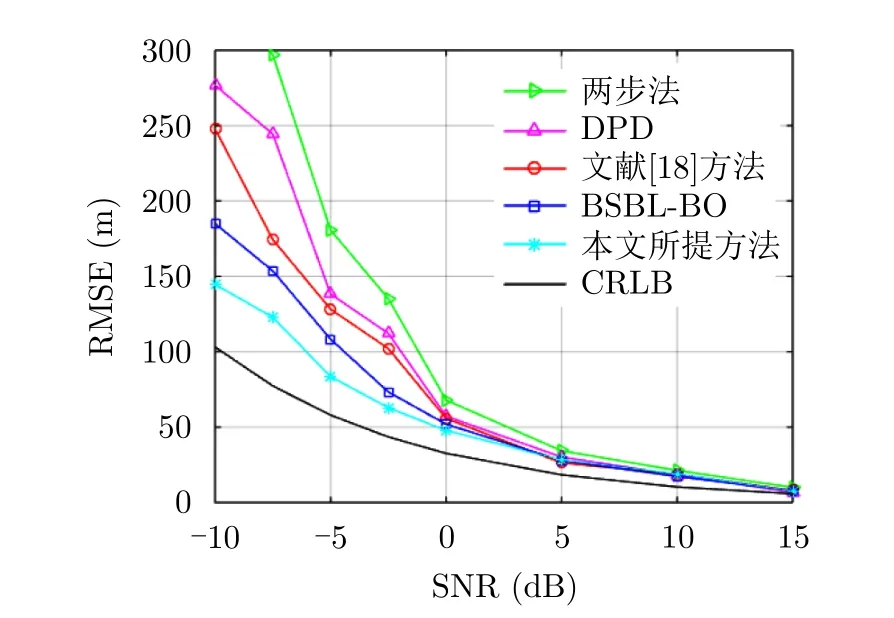
图3 单辐射源下不同定位方法定位结果RMSE随信噪比变化关系Fig.3 Localization RMSE versus SNR using different methods with single emitter

针对不同调制形式的辐射源，利用本文所提方法得到的定位RMSE随信噪比的变化曲线如图4所示。仿真时，阵元数为8，快拍数为64，辐射源发射的BPSK和QPSK信号与单频信号的载频为1 GHz，前两者的带宽均为25 kHz。从图4中可以看出：采用本文所提方法对具有一定带宽的辐射源信号进行定位，能够获得比单频辐射源信号更小的定位误差。

图4 不同调制形式的辐射源定位结果RMSE随信噪比变化关系Fig.4 Localization RMSE versus SNR for the radiation source with different modulations

仿真3：设置两个辐射源分别位于(–0.1,–0.1)和(0.1,0.1) (单位：km)处，发射带宽1 MHz的BPSK调制信号，辐射源距离接收基站的平均距离R约为7.1 km。当快拍数为8，阵元数为10时，采用不同方法得到的定位RMSE相对信噪比的变化曲线如图5所示。可以看出，随着信噪比的增加，除DPD外，其他方法的定位性能都逐渐提高。此外，本文所提出的方法优于其他方法。当信噪比为0 dB时，本文所提方法的RMSE约为辐射源到接收基站平均距离的0.46%，比BSBL-BO方法和文献[18]的方法分别减少0.14%R和0.38%R(R为距离)。DPD是这4种方法中最差的一种，因为在这种情况下它不能有效地区分两个辐射源。因此，它的定位性能不能随着信噪比的增加而大大提高。值得注意的是，随着信噪比的提高，本文所提出的方法性能与BSBL-BO方法基本相同，这是因为本文所提的方法可以看作BSBL-BO方法的推广。

图5 不同定位方法定位结果RMSE随信噪比变化关系Fig.5 Localization RMSE versus SNR using different methods

当SNR为0 dB，阵元数为10时，采用不同方法得到的定位RMSE相对快拍数的变化曲线如图6所示。由此可以观察到，随着快拍数量的增加，所有提出的方法的定位性能都会提高，而DPD基本保持不变。当快拍数为6时，本文所提方法的RMSE约为辐射源到接收基站平均距离的0.67%，比BSBL-BO方法和文献[18]的方法分别减少0.17%R和0.27%R。

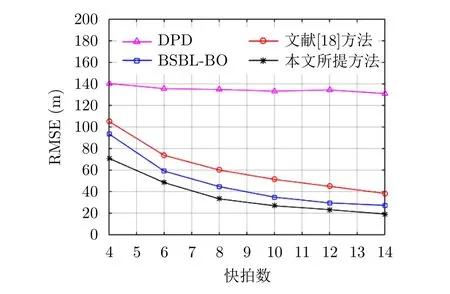
图6 不同定位方法定位结果RMSE随快拍数变化关系Fig.6 Localization RMSE versus number of snapshots using different methods

当SNR为0 dB，快拍数为K=8时，采用不同方法得到的定位RMSE相对阵元数的变化曲线如图7所示。可以看出，随着阵元数的增加，3种方法的性能都会有所提升，阵元数的增加能够提高算法的定位性能。当阵元数为8时，所提方法的RMSE约为辐射源到接收基站平均距离的0.52%，比BSBL-BO方法和文献[18]的方法分别减少0.22%R和0.44%R。

图7 不同定位方法定位结果RMSE随阵元数变化关系Fig.7 Localization RMSE versus number of elements using different methods

6 结论

本文提出了一种基于多字典联合与分层块稀疏贝叶斯框架的多辐射源直接定位方法，将辐射源定位问题转化为多字典的信号恢复问题，同时利用信号在多字典中的共享稀疏性，实现了在传播模型部分未知情况下的辐射源定位。利用Laplace分布的分层块稀疏贝叶斯模型相比传统的贝叶斯学习模型能获得更好的稀疏性，也能获得更优的重构性能。仿真结果表明：与两步法、DPD和文献[18]的方法及BSBL-BO算法相比，本文提出的方法具有更高的分辨率和更优的定位性能，特别是在低信噪比和较少快拍数的情况下。