基于几何约束移动最小二乘的TomoSAR山区点云高精度三维重建方法

李晓婉 梁兴东* 张福博 刘云龙 李焱磊 郭其昌 万阳良 卜祥玺

①(中国科学院空天信息创新研究院微波成像技术国家级重点实验室 北京 100190)

②(中国科学院大学电子电气与通信工程学院 北京 100049)

1 引言

通过对同一观测场景的多角度观测，层析合成孔径雷达(Tomographic Synthetic Aperture Radar,TomoSAR)可以将传统的二维SAR图像拓展到三维图像，已然成为地形测绘、城市监督、生物量估计等三维应用领域中非常有效的数据获取手段[1—3]。

作为典型的自然场景，山区三维重建在地形测绘、资源勘探、灾害评估等方面具有重要意义。然而，TomoSAR山区三维重建主要面临着如下难题：(1)表面覆盖有大量分布式目标，对时间去相关非常敏感[4]；(2)高程跨度大，点云高程模糊问题显著[5]；(3)由于有限的基线长度和通道数量，点云高程向定位精度非常差[6,7]。通过在跨航向布设天线阵列，机载阵列TomoSAR可以有效地提高图像间的时间相关性[8,9]，为山区三维重建提供数据支持，解决了第1个难题。基于分割和重组的高程模糊求解方法可以恢复出无高程模糊的点云[10]，解决了第2个难题。目前针对第3个难题研究较少，迫切地需要提出一种可以提高点云高程向定位精度的TomoSAR山区三维重建方法。

现有的三维重建方法主要是针对TomoSAR和LiDAR提出的。前者多适用于符合平面几何约束模型的建筑物，如RANSAC算法[11]、TomoSeed算法[12]，以及一系列基于建筑物足迹和机器学习的方法[13—15]。显然，这些方法难以用于曲面结构的山区。后者的处理对象较为丰富，常利用法向量和曲率等几何特征、点云分布特征以及拉普拉斯正则化处理等方法进行曲面重建[16—20]。TomoSAR点云密度和LiDAR点云密度相比拟[21]。然而，相比于LiDAR点云，有限基线数量、相参成像和电磁散射特性等因素使得TomoSAR点云的定位精度较差且可能存在离群点和虚假目标等干扰；侧视几何使得TomoSAR点云存在固有的几何畸变问题。因此，LiDAR点云处理方法多难以直接用于TomoSAR山区三维重建[7]。最小二乘(Least-Squares,LS)法在曲线(曲面)散乱点云去噪和曲面拟合等方面得到了广泛的应用[22]。然而，LS追求全局最优，对于复杂点云容易出现过平滑问题。移动最小二乘(Moving Least-Squares,MLS)法利用分段拟合的思想，可以在一定程度上改善过平滑问题[23]。尽管如此，MLS难以实现高精度的TomoSAR山区三维重建。一个原因是坐标系表征问题。雷达坐标系允许只进行高程向定位误差修正，但叠掩使其不满足MLS函数逼近条件。大地坐标系满足此条件，但是山区地形起伏多变，这种对高度向定位误差修正的方式却可能引入更强烈的斜距误差。此外，MLS缺乏对重建结果的几何约束，难以对上述误差进行再次修正。

本文充分地利用了TomoSAR点云高程与地距间的单调递增关系，提出了一种基于几何约束MLS的TomoSAR山区点云三维重建方法。通过投影变化和几何约束MLS两个主要步骤，可以针对性地抑制高程向定位误差。本文的主要创新工作如下：(1)提出了一种新的坐标系投影变换方法，这是利用几何约束进行高程定位误差修正的前提；(2)将TomoSAR点云的几何约束关系融入MLS，保证了重建结果的全局约束性；(3)提出了一种几何约束MLS迭代求解算法，保证了结果的准确性。

2 TomoSAR点云几何约束模型

TomoSAR通过多角度观测实现了叠掩地形的高程分辨。图1示意了TomoSAR山区观测几何，黑色原点示意阵列天线，红色加粗曲线示意被照射山区地形，黑色加粗曲线示意被遮挡山区地形，H对应载机高度，P1,P2和 P3叠掩在一起。假设基线均匀分布，最左侧通道为主通道，对于观测目标 P2，第n个通道与主通道间的相位差可以表示为[24]

图1 TomoSAR山区观测几何示意图(y和z分别表示地距向和高度向，r和s分别表示斜距向和高程向)Fig.1 Diagram of TomoSAR mountain observation geometry (y and z indicate the ground direction and the height direction,respectively,r and s indicate the range direction and the elevation direction,respectively)

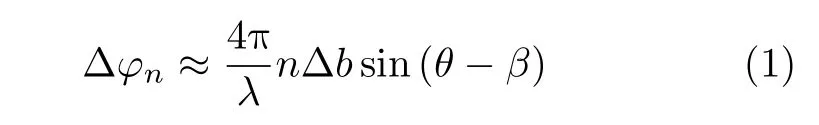
其中，λ是波长，Δb是相邻通道间的基线长度，θ是被观测目标相对于主通道的入射角，β是基线水平倾角。

根据压缩感知高程分辨求解模型，第n个通道与主通道间的相位差也可以表示为[25]

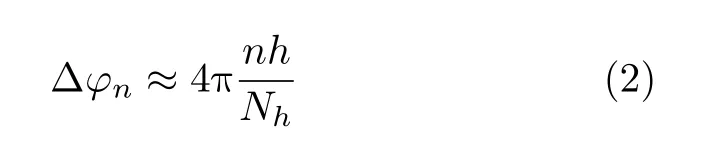
其中，Nh是一个高程周期的离散点数，h是高程向谱估计值。

令ρs表示高程向超分辨率，h与真实高程值s间的关系为s=hρs。其中，真实高程值为目标的高程向距离，即地距-高度平面原点o相距目标所在方位-斜距平面的高程向距离。以观测目标 P2为例，其斜距值和真实高程值分别为r2和s2。为了简便，下述内容均将h称为高程值。

联立式(1)和式(2)，可以得出

简化常数项，高程值可以进一步表示为

其中，常数项k=λ/2ΔbNh。

通常来说，0＜β ＜π/2，下视角0＜θ ＜π/2。在这种情况下，目标高程值与下视角具有单调递增关系。同时，照射几何表明，只有下视角随地距增加而增加的点才会被照射到。如图1所示，P1,P2和 P3满足照射几何，均可以被照射到，其高程值随地距增加而增加。尽管 P4和 P5对应地距范围内黑色加粗地形不会被照射到，但其在TomoSAR点云中表现为两端高程连续的空洞区域，不会破坏这种单调递增关系。这是因为 P4和 P5的下视角相同，由式(4)可以推得其高程值也相同。

综上，TomoSAR点云高程与地距具有单调递增几何约束关系。

3 几何约束移动最小二乘方法

本文方法的流程图见图2，主要包括投影变换和几何约束MLS这两个步骤。下面对其进行详细介绍。

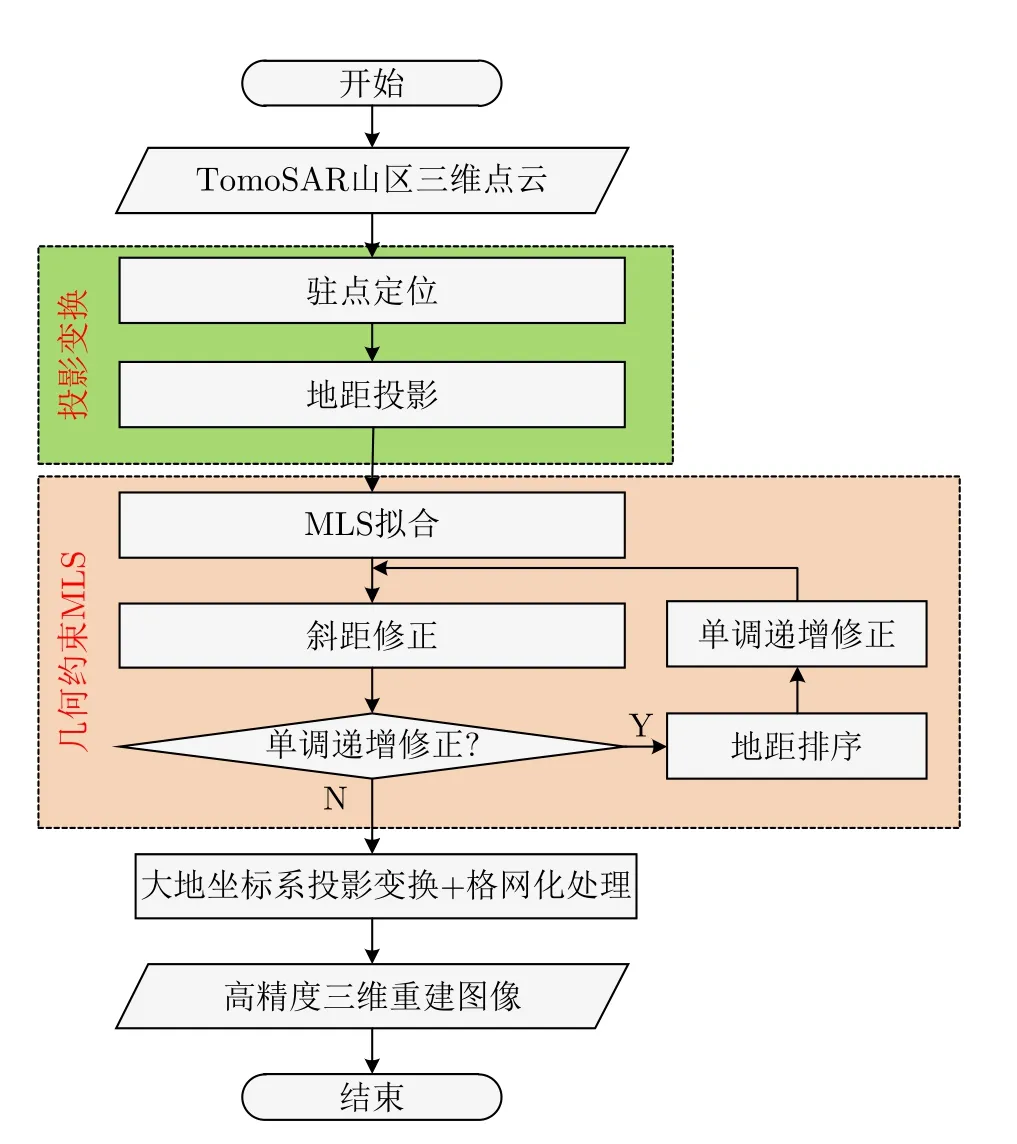
图2 几何约束MLS方法流程图Fig.2 Flowchart of the geometry constrained MLS method

3.1 投影变换

投影变换主要包括驻点定位和地距投影两步。前者用于估计原始散射点的地距顺序，后者用于按照已知地距顺序对原始散射点进行地距重排，从而避免地距倒置带来的约束失效问题。

3.1.1 驻点定位

图3示意了常见的S形山区叠掩地形。A和B称为地形驻点，其具有位于左向开口或右向开口的U形曲线斜距边缘的特性。以地形驻点高程为门限可以将地形分为I区，II区和III区3个部分。I区和III区内点云呈现出正斜率走势，真实地距随斜距增加而增加；II区内点云呈现出负斜率走势，真实地距随斜距减少而增加。由此可见，在正确定位驻点后，可以利用相邻驻点高程区间内散射点的斜率特性估计出原始散射点的相对地距关系。

图3 斜距-高程平面S形山区叠掩地形结构图Fig.3 The S shaped layover mountainous terrain on the range-elevation plane

山区地形复杂多变，且存在地形遮挡等问题。TomoSAR山区点云还可能呈现出如图4所示的更复杂形状，但不影响上述规律。为此，本文利用二分递归思想进行分区驻点定位，具体步骤如下：

步骤1 利用同一方位-斜距单元内叠掩目标的高程跨度远大于非叠掩目标高程跨度的特性执行叠掩地形判断。具体地说，只要检测地形中高程跨度大于阈值Th的点数大于阈值Tnum，就将其视为叠掩地形，并进入步骤2。反之，将其视为非叠掩地形，进入步骤3；

步骤2 利用前述驻点特性执行驻点检测。首先检测斜距边缘点。为了避免上下边界点的影响，只有与输入数据边界点的斜距向距离和高程向距离大于阈值Trdis1和阈值Thdis1的点会被保留。最后，会进一步判断边缘点是否符合U形曲线特征。对于右向开口曲线，位于边缘点左侧Trdis2和Thdis2矩形框内的邻域点数需小于阈值Tnei，同时，还需要输入数据中存在位于其右侧高程两侧且与其斜距向距离大于Tr的点。左向开口曲线判断准则与之相反。如图4(a)，点A和点T为斜距边缘点。但是，点T为边界点会被舍弃。又因为点A符合右向开口U形曲线特征，会被检测为驻点。

步骤3 下述内容均以dataij表示以pi和pj为上下边界的待检测地形，fact(dataij) 表示对待检测地形dataij进行驻点定位。如图4(a)，data12则对应以p1和p2为上下边界的待检测地形，fact(data12)对应主函数。下面分3种情况执行二分递归。

(1) 情况1为非叠掩地形，输出结果为空且会结束驻点定位；

(2) 情况2为叠掩地形且已经检测到驻点的情况。这时会对两个边界点和驻点进行高程排序，并对相邻点内的地形进行递归。如图4(a)所示，对驻点A (p3)和两个边界点排序后，相邻点内的地形为data13和data23，输出结果为p3∪fact(data13)∪fact(data23)；

(3) 情况3为叠掩地形但没有检测到驻点的情况。如图4(b)，p3为高程向区间二分后确定的分割点，使用二分法递归执行主函数。不考虑p3恰好为驻点的情况时，输出结果为 fact(data13)∪fact(data23)。显然，这可能会漏检恰好同为驻点和分割点的点p3。为了避免这种情况的发生，会在位于p3上方的驻点和边界点中找到与其高程距离最小的点p4，同理，会在p3下方找到p5，并再次执行f act(data45)，输出结果为fact (data13)∪fact (data23)∪fact(data45)。

图4 两种典型地形驻点定位示意Fig.4 Diagram of two typical terrain for stagnation point positioning

综上，驻点定位主函数f act(data)为

3.1.2 地距投影

步骤1 方位向循环：

(1) 以驻点高程升序的方式估计所有高程向相邻驻点间点的斜率；

(2) 对于正向斜率区域，以斜距升序方式调整点的顺序；对于负向斜率区域，以斜距降序方式调整点的顺序；

(4) 根据式(3)计算排序后点的地距：yn=rnsinθn；

(5) 保持每个散射点的方位和高程不变，投影坐标系表征的点为

步骤2 结束循环；

步骤3 输出投影变换后的点：P′={pi(ai,yi,hi)|ai ∈(A1,A2,...,AJ),i=1,2,...,Ntotal}及其斜距r={ri|i=1,2,...,Ntotal}。

图5说明了地距倒置导致几何约束失效的问题，这也是进行地距投影的主要原因。图5(a)示意斜距-高程平面的散射点，图5(b)示意地距-高程平面内的散射点。可以看出，受高程向定位误差影响，点地距倒置，而且这使得几何约束失效。通过驻点定位和斜率估计可以推断出点位于II区，所以由可以推断出这两个点的真实地距顺序。点示意了按照真实地距排序的点可以看出，点不再满足单调递增约束关系，几何约束MLS可以对其进行再次修正。

图5 投影变换示意Fig.5 Diagram of projection transform

3.2 几何约束MLS

3.2.1 函数模型

参考MLS局部加权的思想，任意点pn,n=1,2,...,N，局部子空间内几何约束MLS代价函数为

其中，第1项为MLS惩罚项，w(pi-pn)是点pn处具有紧支撑特性的光滑连续权函数，f(pi)是局部子空间的拟合函数；第2项为单调递增惩罚项，单调递增惩罚因子κ大 于0，κ越大，单调递增约束越紧，vn是单调递增惩罚局部子空间的权函数。

令影响域半径r=‖pi-pn‖/dmI，高斯权函数w(pi-pn)[26]为

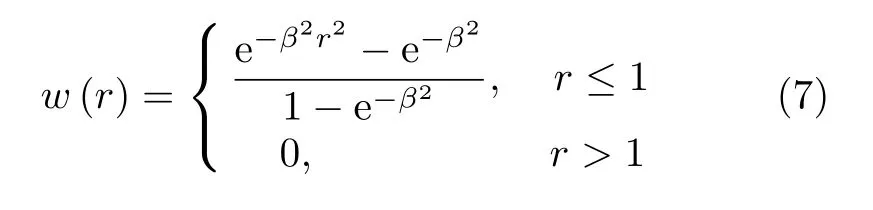
其中，dmI 决定局部子空间的大小，β决定权函数的衰减速度。

拟合函数可以表示为

其中，多项式函数矩阵D(p)的展开式为

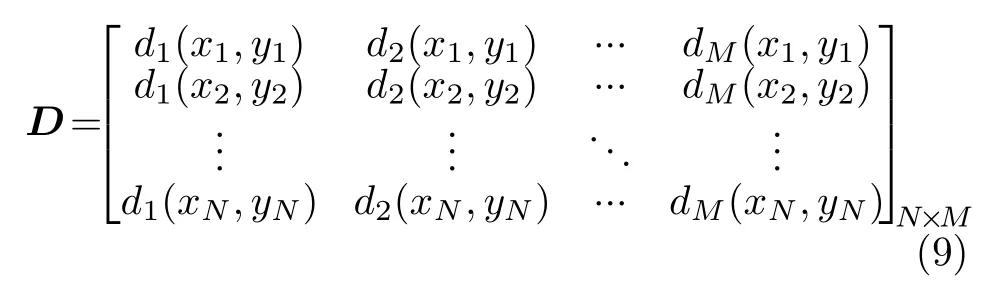
待求系数c=[c1c2...cM]T,d(x,y)=[d1d2...dM]T是最高次数为M的多项式基函数。

权函数v=[v1v2...vN]T需要保证只有在拟合结果违背单调递增约束时，几何约束惩罚项才起作用。任意点pn相 对其邻域子空间p win的单调递增权函数可以表示为

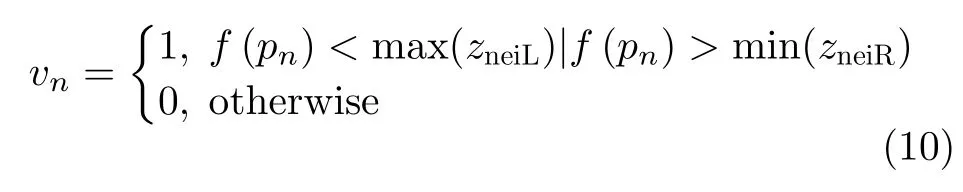
其中，zneiL和zneiR分别是与点pn方位向相同且位于其左右两侧的p win个邻域点的第三维信息。

3.2.2 问题求解

几何约束MLS的解析解可以表示为

权函数矩阵W是对角元素为w(pi-pn)的对角阵，单调递增权函数V是对角元素为vi的单位阵。

然而，下述几点不足使得符合单调递增约束的解析解难以得到：(1)矩阵V与解析解耦合。也就是说，需要先给定多个解析解，才能求出对应的矩阵V以及代价函数，最后再进行最小代价函数查找才能确定最优解，计算代价很大；(2)每个局部子空间内点的分布不一致，对应MLS惩罚项拟合误差也不一致。所以，最好根据子空间数据分布设置N个单调递增惩罚因子κ。显然，这是比较困难的；(3)对于表现为下降趋势的输入数据，无法满足单调递增约束。

于是，本文给出了一种迭代求解方法。针对问题(1)，该方法采取先执行MLS后针对性地对非单调递增点进行高程修正的策略。这是因为当单调递增惩罚项为0时，MLS结果就是几何约束MLS结果；针对问题(2)，引入不小于0的局部抖动因子dh，这可以将拟合结果的高程抖动限定在dh内；针对问题(3)，迭代修正可以重复修正不满足单调递增约束的点。整个几何约束MLS求解算法见表1。对于MLS求解，本文采用不断放大dmI的策略来自适应确定影响域半径，直到其满足MLS求解的非病态条件。此外，与格网化的MLS求解流程[27]不同的是，为了保证斜距不变性，本文会先求所有点MLS拟合结果。最后，通过大地坐标系投影变换和均匀格网化处理[27]得到重建结果。

表1 几何约束MLS求解算法Tab.1 The solution algorithm of the geometry constrained MLS

4 实验结果分析

为了验证所提方法的有效性，给出了仿真数据和实测数据的处理结果。作为对比，给出了传统的大地坐标系下执行的LS[22]和MLS[27]处理结果。

4.1 参数设置讨论

投影变换参数对数据敏感度较高，需要根据实际数据进行经验选取，以保证驻点的U形分布特性。几何约束MLS参数对数据敏感度较低。参数pwin值越大，单调递增权函数vn为1的概率越高，会导致迭代求解的效率变低。考虑到本文以地距升序局部单调递增修正的方式来达到全局单调递增，将其设为 pwin=2。当对同一点相邻两次修正的效果de小于阈值Te时，会进入到下一点，文中将其设为Te=1e-5 。抖动因子 dh越小，单调递增约束越紧，反之，单调递增约束越松，允许结果存在 dh范围内的高程抖动。因此，在数据质量好且单调递增约束紧时，其最小值为0。否则，可以对其进行适当放大。此外，对于MLS求解，本文选用二次基和高斯权函数。dmI初始化为原始点云地距分辨率ρy的3倍，且以2倍的乘因子进行放大。参数β对重建结果也会有一定程度的影响，可以根据不同数据进行合理设置，文中将其设为3。

综上，本文中几何约束MLS求解参数设置为：pwin=2,T e=1e-5,d mI=3ρy,β=3。其他参数就要根据数据进行经验设置。作为对比，LS多项式拟合阶数设置为5，MLS的参数同本文方法。此外，3种方法的格网化节点一致，均为5 m。

4.2 仿真实验

4.2.1 数据生成

图6给出了LS,MLS和本文方法对于4种不同地形的仿真数据处理结果。数据1为连续的S形地形，数据2为底部被遮挡住的地形，数据3和数据4示意包含一个和多个S形地形的复杂地形。数据1由3次样条曲线生成，数据2到数据4地形更为复杂，是以AW3D30 DSM数据[28]为输入的POV-RAY软件[29]输出数据。其中，POV-RAY软件用于模拟地形遮挡情况。最后，通过在高程向上加入均值为0，标准差为2.5个高程向像素单元的高斯白噪声模拟高程向定位误差。仿真系统参数同下述实测实验。对于场景中心，地距分辨率约为0.5 m。

图6 LS,MLS和本文方法的仿真结果Fig.6 Simulation results of LS,MLS and the proposed method

4.2.2 结果与分析

数据1和数据2的投影变换参数设置为：T h=10,Tnum=10,T rdis1=100,T hdis1=5,T rdis2=5,Thdis2=2,T nei=5,T r=20。数据3的不同参数为：Trdis1=10,T r=48。数据4的不同参数为：Trdis1=10,T r=12。此外，数据1的抖动因子d h=0.3，其他数据为d h=1.2。

下面定性分析3种方法的重建性能。可以看出，全局多项式拟合的LS过平滑问题非常突出，MLS可以对其进行一定程度的改进，但是在驻点邻近区域内会引入斜距误差。本文方法只进行高程向定位误差修正，可以很好地避免引入斜距误差，最接近于真值，尤其在驻点邻近区域。

然后，以绝对测高精度为评估指标[30]，给出定量化评估结果。3种方法处理结果的格网节点一致，且有与其一一对应的真值。原始点云非均匀分布，利用线性插值进行格网化。因此，绝对测高精度为重建结果与其对应真值的高度向均方根误差，下述称为精度。表2列出了4种数据的精度。可以看出，LS和MLS在追求平滑的同时，可能降低原始点云的精度，如数据2；MLS可以在一定程度上提高LS的重建精度，尤其是对于数据3和数据4这种复杂地形；本文方法均可以将MLS的定位误差降低至原来的1/2左右。进一步地，图7呈现了不同方法的精度对比曲线。输入为加入不同高程向误差的数据1。以高程向像素数为单位，10个切片的高斯白噪声的标准差依次为：0.5,1.0,1.5,2.0,2.5,3.0,3.5,4.0,4.5,5.0,均值为0。可以看出对于同一切片，所提方法性能最优；随噪声增加，3种方法的定位效果均下降，但是所提方法性能下降缓慢，且逐渐显著优于MLS。

图7 基于数据1的不同方法的精度对比曲线Fig.7 The precision comparison curves of different methods based on data 1

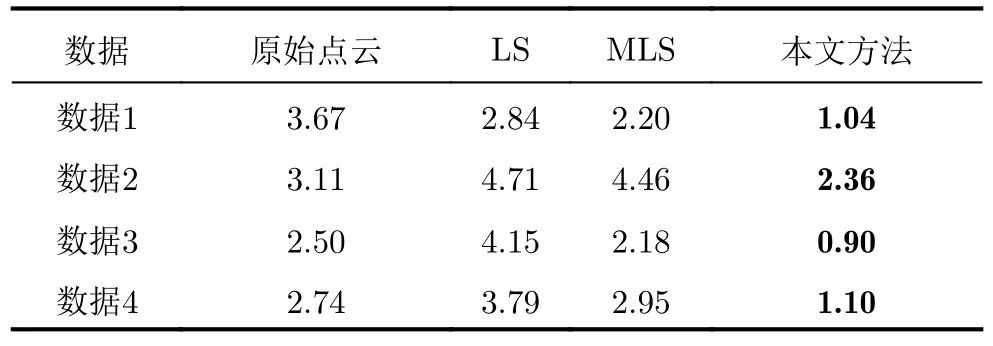
表2 仿真结果精度(m)Tab.2 Precision of the simulated results (m)

最后，图8呈现了本文方法对于切片5的主要中间结果。图8(a)中原始点云被赋予颜色图，值越接近1，由投影变换预测得到的地距值越大。可以看出，真值的高程和地距满足单调递增关系，原始点云地距乱序分布。此外，MLS结果满足单调递增条件，但在驻点邻近区域误差较大。如图8(b)所示，驻点定位实现正确分区，斜距修正后的MLS结果不再满足单调递增条件，需要进行迭代修正。图8(c)是斜距修正MLS结果的地距排序结果，这里有很多非单调递增点。图8(d)示意的是地距-高程平面的重建结果。通过迭代执行单调递增修正和斜距修正等处理，重建结果满足单调递增约束条件。最后，执行大地坐标系投影变换和格网化处理，即可得到最终的重建结果。

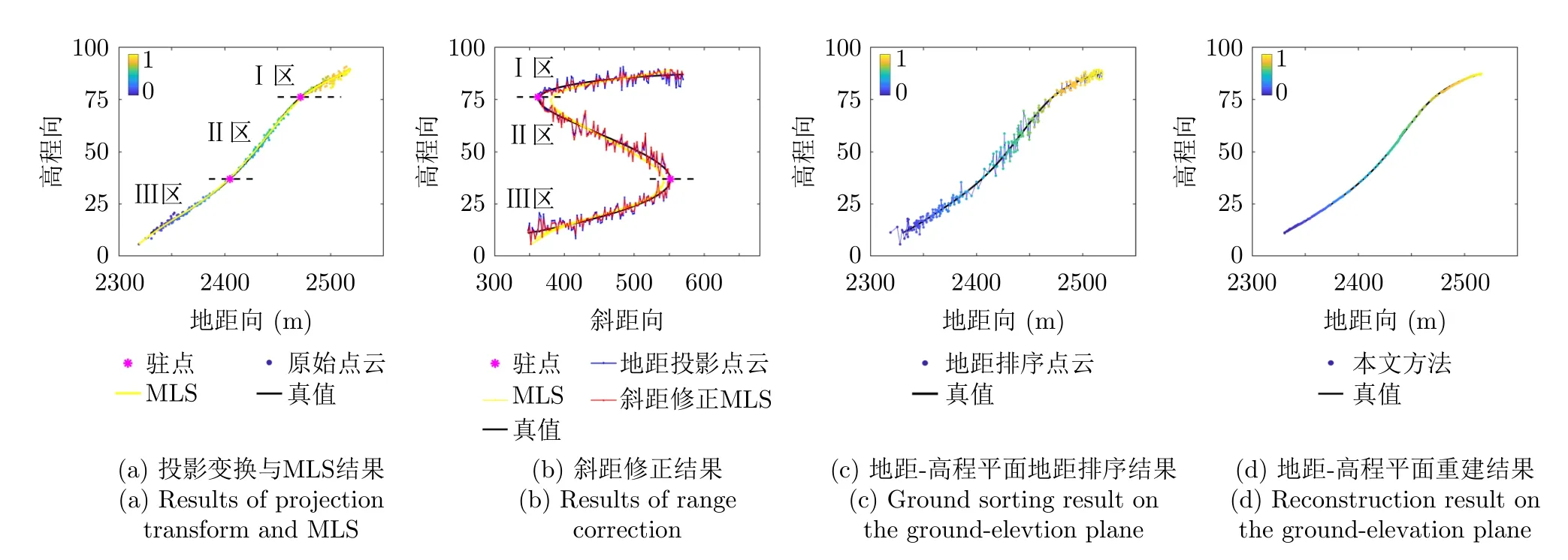
图8 本文方法对于切片5的主要中间结果Fig.8 The main intermediate results of the proposed method for slice 5

4.3 实测实验

4.3.1 数据介绍

2019年，我们团队在中国四川省乐山市市域内的黄泥巴山区开展了机载阵列TomoSAR飞行实验。系统工作在X-波段。天线阵列由沿水平向均匀的12个天线构成，基线间隔是0.2 m。详细的系统参数见表3。在获得回波数据后，依次执行SAR图像生成、图像配准、高程分辨和高程模糊求解[10]。一个高程周期的离散点数是128。

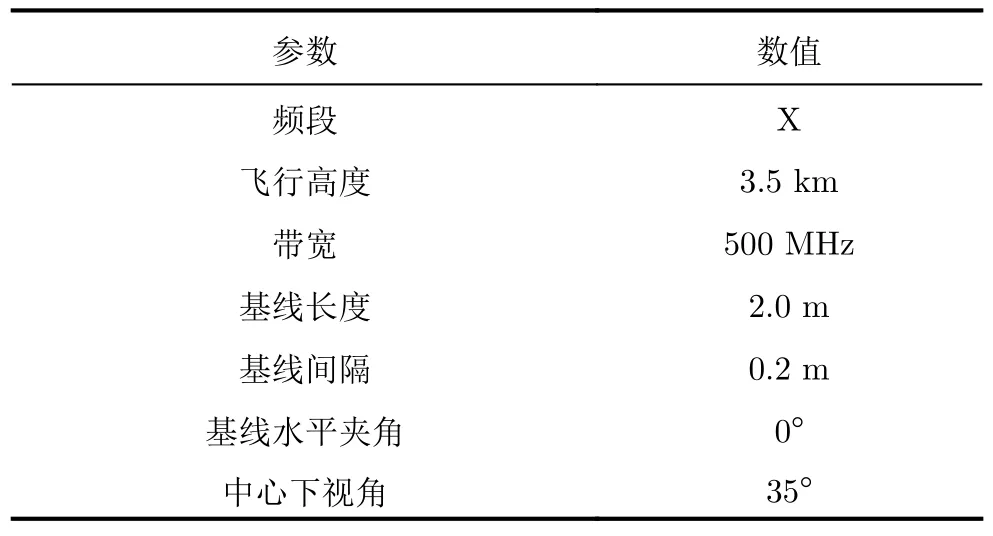
表3 主要实验参数Tab.3 Main experimental parameters

4.3.2 结果与分析

图9是观测场景的SAR图像。场景的像素数是7500×6800 (方位×地距)。方位向和斜距向像素大小约为0.11 m和0.14 m。图10呈现了SAR图像中3个典型切片的地距-高度平面和斜距-高程平面的处理结果，其中蓝色点为TomoSAR点云数据。除了切片2的 Trdis1=80,T r=40，所有切片投影变换参数同仿真数据1。抖动因子均设为1.2。AW3D30 DSM和1:10000 DEM两种外源数据用作参考值。DSM格网间隔为30 m，标称测高精度为5 m。DEM格网间隔为5 m，平地高程中误差高达1 m，但高山地高程中误差是6.7 m。为了对比更多的细节，本文呈现的两种外源数据是经global mapper软件1 m格网化处理后的结果。相比于DEM，DSM包含了地表地物的高度。在无误差的情况下，对于同一观测目标，DSM数据的高度应该不小于DEM。然而，在局部区域，DSM数据的高度小于DEM，如矩形框2。这种情况可能由插值处理或者是两种数据本身的测高误差导致。因此，本文只利用两种外源数据来定性分析3种方法的重建性能。此外，实测数据存在斜距误差，执行几何约束MLS前需要对同一高程向上的点取斜距平均进行抑制。

图9 观测场景的SAR图像(颜色图表示归一化后的散射强度)Fig.9 SAR image of the observation scene (the color map indicates the normalized scattering intensity)

首先，分析TomoSAR点云精度。整体来看，原始点云走势与两种外源数据几乎一致。而且对于DSM高于DEM的区域(如矩形框1)，同样包含地物高度信息的原始点云更接近于DSM，符合实际情况。需要说明的是，本文呈现的原始点云数据存在非均匀基线导致的局部偏差问题，如图10(b)中高程值为128的点。但这种局部偏差仍然可以等效为高程误差，并不影响本文方法有效性的验证。

然后，分析3种方法的重建性能。可以看出，LS结果显著偏离原始点云和两种外源数据，MLS和所提方法结果走势和两种外源数据几乎一致。但是，如图10(c)两个局部放大矩形框所示，MLS和所提方法结果高度差高达10 m。进一步地，根据图10(b)、图10(d)和图10(f)中矩形框可以推断，所提方法处理结果更贴近原始点云，符合叠掩地形的S形曲线特征，而MLS结果在追求平滑的同时带来了斜距误差。因此，对于山区叠掩地形，尤其是驻点邻近区域，所提方法重建精度更高。

图10 实测实验的处理结果Fig.10 Results of the real experiment

最后，图11呈现了观测场景的光学图像。矩形框示意了重建区域，其大小是800 m×1400 m (方位×地距)。图12呈现了本文方法重建的三维图像。该场景的SAR图像见图9。可以看出，TomoSAR山区三维重建图像与光学图像基本一致：两座主峰分别位于重建的北侧和东侧，两峰之间有明显的沟壑；主峰1处的中部有一处凹陷。此外，本文结果和DSM的高度变化范围都是600～1200 m。

图11 观测场景的光学图像Fig.11 Optical image of the observation scene

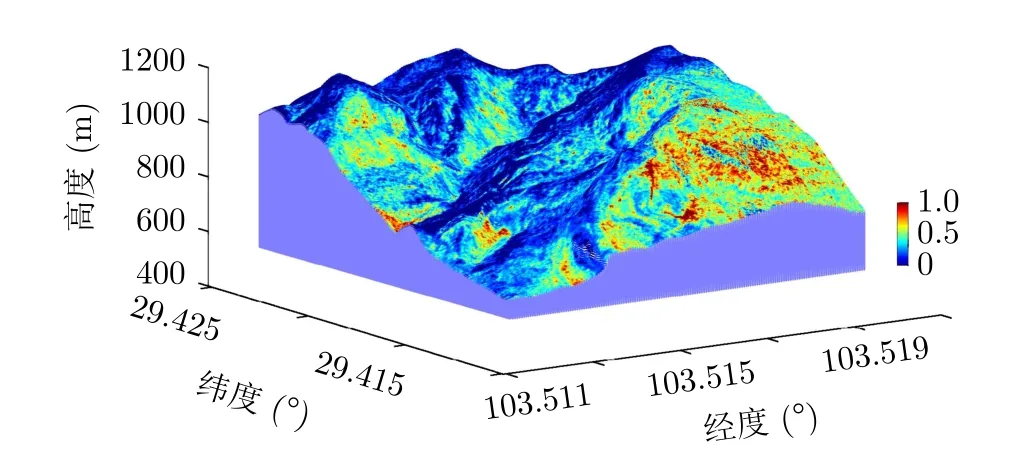
图12 三维重建图像(颜色图表示归一化后的散射强度)Fig.12 The three-dimensional reconstruction image (the color map indicates the normalized scattering intensity)

4.4 影响因素分析

首先，分析高程向噪声对驻点定位和地距投影的影响。对于实测点云数据中可能存在的离群点和虚假目标，需要在高程模糊求解步骤进行去除[10]，本文不做分析。噪声对驻点定位的影响可以分为定位误差、虚警和漏检3种。定位误差和虚警对地距投影以及重建精度影响不大。然而，漏检会导致本文方法的重建精度急剧下降，且可能会显著低于MLS。这是因为，本文方法的核心思想是利用TomoSAR点云地距和高程间的单调递增关系进行高程修正，而驻点定位和地距投影是正确预判点云地距相对顺序的关键。

地形遮挡是山区三维重建中较常见的现象。如图8(a)和图8(b)所示，I区位于地形上部，II区位于地形中部，III区位于地形底部。那么，驻点A相邻区域几乎不会被遮挡住。虽然驻点B相邻区域以及II区底部可能因为前侧地形遮挡或者照射不完全等问题导致对应点云数据丢失，如图6中数据2和图10中切片3，但本文方法对这种情况很鲁棒。同时，根据TomoSAR点云的高程单调递增关系可知，虽然在I区相距驻点较远的位置可能出现点云空洞(如图10(f))，但不会破坏单调递增特性。因此，本文方法对地形遮挡现象很鲁棒，且会通过格网化插值处理对这些空洞区进行填充。

综上，本文方法对地形遮挡现象较鲁棒，但对驻点漏检导致的地距预判顺序严重错误的情况非常敏感。因此，对于被噪声严重破坏的原始点云，要通过合适的投影参数设置、去噪等预处理甚至是人工干预来避免驻点漏检等情况的发生。

5 结论

TomoSAR山区三维重建是三维成像领域的前沿研究。本文针对TomoSAR山区点云高程向定位精度差的问题，推导了TomoSAR点云几何约束模型，进而提出了一种基于几何约束MLS的三维重建方法。通过驻点定位和地距投影，雷达坐标系表征的点可以被投影到新的方位-地距-高程坐标系，几何约束得以利用。通过在MLS代价函数中引入单调递增约束惩罚项，所提方法可以针对性地对斜距修正后不满足单调递增约束的MLS拟合结果进行高程向定位误差修正，进而提高了三维重建精度。仿真和实测的机载阵列TomoSAR山区数据处理结果验证了本文方法的有效性，对于仿真数据结果，本文方法相比LS和MLS重建精度提高一倍以上。而且，相比于DSM数据和DEM数据，本文重建结果在水平分辨率和散射信息恢复等方面具有显著的优势，有望用于一些需要精细化地形地貌支撑的军事侦察和灾难评估等应用。未来，我们也将关注原始点云高精度生成等处理，以得到更高精度的TomoSAR山区三维重建结果。