一种双极化气象雷达自适应谱极化滤波方法

安孟昀 殷加鹏 黄建开 庞 晨 李永祯 王雪松

(国防科技大学电子信息系统复杂电磁环境效应国家重点实验室 长沙 410073)

1 引言

气象雷达可实现对大气的高时空分辨率观测，是大气观测必不可少的工具[1,2]。具有极化测量能力的多普勒气象雷达获得的信息被广泛应用于定量降水估计[2—5]、短期天气预报[6]和预警[7]等方面。多普勒和极化信息相结合可以反映采样体积中分布目标的微物理和动力学特性，显著提高定量降水估计性能。在气象观测中，利用雷达数据进行降水估计的前提是数据要有足够的精度，但是由于雷达工作环境较复杂，雷达数据经常受到杂波的影响[8]，例如地杂波、海杂波、生物回波、射频干扰[9]等。这些杂波会影响气象目标的反射率、多普勒速度和极化参量的测量与估计，进而影响降雨估计和微物理研究。因此，有效的杂波抑制方法研究十分重要[10]。

气象雷达杂波根据多普勒速度的不同可以分为静态杂波(即地杂波)和动态杂波。对于地杂波，传统的方法是通过以零速度为中心的凹口滤波器来抑制，其性能取决于地杂波的谱宽[2,11]。为解决窄带零速度气象信号的损失问题，文献[12]提出了高斯模型自适应处理方法(Gaussian Model Adaptive Processing,GMAP)。但是，当GMAP作用于未被杂波影响的距离单元时，降雨目标反射率的估计值会降低。因此，在应用这些杂波抑制方法之前需要先检测杂波是否存在。常用的检测算法有杂波抑制决策(Clutter Mitigation Decision,CMD)算法[13,14]和谱杂波识别(Spectrum Clutter Identification,SCI)[15]算法。在实际中无论是CMD算法还是SCI算法都会造成降雨目标的漏判和误判。文献[16]提出了一种模糊算法识别并去除地杂波，这种方法在提高地杂波识别率的同时也会造成降雨目标的损失。为了将杂波检测和滤波集成到一种算法中，文献[17]提出自适应杂波环境分析法(Clutter Environment Analysis Using Adaptive Processing,CLEANAP)，它利用幅度和相位来改变凹口滤波器的凹口宽度，使气象目标估计的偏差更小。为了在滤波的同时保留较完整的降雨目标，文献[18]提出一种时域回归滤波技术，该技术提高了对降雨目标的估计性能，但是该方法还未得到实测数据的验证。

除了上面提到的杂波，带状杂波也会影响气象雷达数据的精度[10]。带状杂波是由雷达系统本身或外部辐射源造成的。大多情况下，这些杂波并不局限于某些距离单元，且在距离-多普勒(Range Doppler,RD)域中是非平稳的，这使得传统的杂波抑制方法无法滤除此类杂波[10,19]。目前，荷兰代尔夫特理工大学研制的IDRA (IRCTR Drizzlc Radar)雷达的带状杂波抑制处理是在RD图(PPI的每个方位向)上进行的，它由以0 ms—1为中心的窄凹口滤波器和双谱线性去极化比滤波器(Double spectral Linear Depolarization Ratio,DsLDR)组成[20]。但是由于降雨和杂波的谱线性退极化比(spectral Linear Depolarization Ratio，sLDR)有所重叠，DsLDR滤波器无法将它们完全分开。此外，凹口滤波器在去除噪声的同时会损失弱降雨目标[10]，导致剩余的降雨区域不连续。为了解决上述问题，Yin等人[10]提出移动双谱线性去极化比(Moving Double spectral Linear Depolarization Ratio,MDsLDR)滤波器，该滤波器利用降雨在RD图上连续分布这一特征，用数学形态学方法补偿缺失的降雨。虽然sLDR可以用来区分降雨、噪声与杂波，但是它很容易受到噪声的影响，引入测量误差[20,21]，且该方法只适用于全极化雷达。为了解决这一问题，Yin等人[22]提出移动谱去极化比(Moving spectral Depolarization Ratio,MsDR)滤波器，该滤波器引入更稳健的sDR参量。MsDR滤波器还可解决无交叉极化测量能力的双极化雷达的杂波抑制问题。

MDsLDR滤波器和MsDR滤波器都运用了谱极化滤波技术，利用降雨目标和非降雨目标的谱极化特性在RD图上的连通特性差异，在尽可能多地保留降雨目标的同时滤除非降雨目标。谱极化滤波技术是根据信噪比与对应滤波参数的关系，以及杂波和降雨的去除比例来确定滤波阈值，利用此阈值在RD图上产生一个 {0,1}的二值滤波值，作用于原始的功率谱，实现降雨目标的保留和杂波的滤除[21,22]。但是，在实际PPI扫描中，不同方位向上的降雨情况存在差异，且杂波和噪声依赖该方位向的地理环境。为了获得较好的滤波效果和降雨估计，根据每个方位向回波情况选取阈值显得尤为重要。

本文提出的自适应移动谱去极化比(Adaptive Moving spectral Depolarization Ratio,AMsDR)滤波方法可以根据每个方位向回波情况以及气象目标和杂波在RD图上的差异进行气象目标的保留与杂波的滤除。首先，为了解决双极化雷达的杂波抑制问题，本文根据气象目标的谱极化特性构造sDR参数。其次，本文利用气象目标和杂波的詹森-香农(Jensen-Shannon,JS)散度确定各径向扫描的滤波阈值，在RD图上生成一个二元掩模。然后，结合数学形态学方法恢复降雨，最终实现自适应谱极化滤波。本文提出的自适应谱极化滤波器可以广泛应用于双极化气象雷达以及全极化气象雷达。

本文的结构如下：第2节主要介绍极化多普勒气象雷达的典型参量；第3节阐述AMsDR滤波器的设计步骤，并提出逐个方位向确定阈值的算法；第4节应用实测数据对滤波器的滤波效果进行验证；最后对本文工作进行总结。

2 谱极化参量

谱极化技术利用多普勒和极化信息综合表征气象目标的微物理和运动特征，有利于反演气象目标和抑制非气象目标回波。下面介绍几种典型极化气象雷达测量参量[21]。

假设极化气象雷达发射x极化电磁波、接收y极化电磁波，其中x,y ∈{h,v}，h 表示水平极化，v表示垂直极化。基于后向散射的约束，与距离r和多普勒速度v相关的谱反射功率定义为

其中，C为雷达常数，sSxy(r,v)表示二维的复距离-多普勒谱，sPxy(r,v)表示谱功率。定义谱差分反射率 sZdr(r,v)、谱共极化相关系数sρco(r,v)、谱去极化比s DR(r,v)为[21,22]

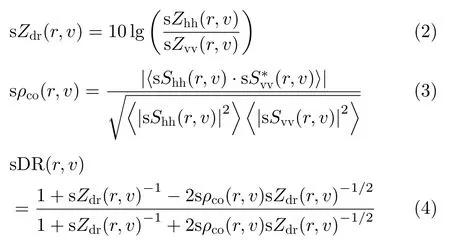
其中，sρco(r,v)中的〈〉表示在距离维或多普勒速度维的滑动平均，在本文中为后者，*表示复共轭。利用RD图进行谱极化滤波之后，杂波和噪声被滤除的同时保留降雨目标，可以更准确地估计测量参数。

3 AMsDR滤波器设计

3.1 AMsDR滤波器滤波步骤

利用降雨目标和非降雨目标的谱极化特性和在RD图上连通特性的差异，谱极化滤波技术可以在尽可能多保留降雨目标的同时滤除非降雨目标。其中，MsDR滤波器提出的初衷是为了解决大部分同时发射同时接收(Simultaneous Transmission and Simultaneous Reception,STSR)模式的业务气象雷达的杂波滤除问题。该滤波器主要分为4个步骤，第1步利用谱去极化比滤波器滤波，第2步是沿着多普勒维使用一个动态窗滤除带状杂波，第3步是利用二维的动态窗恢复去除的降雨滤除剩余杂波；最后，用数学形态学方法进一步恢复降雨信号。

为了能够在有效去除杂波的同时保留降雨目标，本文提出一种AMsDR滤波方法。该方法可以根据每个方位向的数据情况自适应地进行谱极化滤波。AMsDR滤波器的设计主要包括以下6个部分，如图1所示。

图1 AMsDR滤波器流程图Fig.1 Flow chart of the AMsDR filter

步骤1 自适应阈值选取。根据降雨目标与非降雨目标的谱极化参量在统计特性上的差异，利用JS散度确定谱极化滤波的阈值。其中阈值选取方法将在3.2节用真实的雷达数据讨论。

步骤2 谱极化滤波。利用步骤1中求得的阈值进行谱极化滤波，得到{ 0,1}二元掩模，其中“0”表示杂波，“1”表示降雨目标。该二元掩模作用于原始的RD功率谱以提取降雨目标并滤除杂波[10]。

步骤3 一维多普勒滑动窗选取降雨目标。基于对带状杂波谱宽的分析，设置长度为M的多普勒移动窗口，将中心单元以及其前后的M/2个单元视为一个整体。将移动窗口应用于步骤2中获得的掩模，当移动窗口在多普勒谱中从第1个单元移动到最后一个单元时，如果移动窗口的任何位置有0，那么将中心单元替换为0，否则保持1。通过此过程，获得滤波后的掩模[10]。

步骤4 二维滑动窗恢复降雨并滤除杂波。步骤3的处理几乎会滤除所有的带状杂波，但是同时会损失一些降雨。为了进一步滤除剩余的杂波并恢复降雨，对步骤3得到的滤波后的掩模应用一个3×3大小的移动二维窗口[10]。将移动窗口的中心对齐到选择的RD单元，得到此RD单元邻近的9个值[M1,M2,...,M9]，然后对这9个元素求和得到

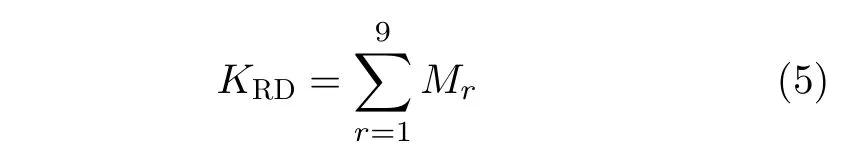
通过设置一个阈值TRD来决定该RD单元的滤波掩模MRD，即

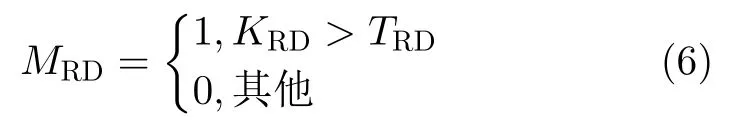
其中，阈值TRD是根据降水和杂波的去除比例，并结合降雨目标滤波前后的最小均方误差决定的，具体选取方法见文献[10]。

通过此移动二维窗口，可以进一步去除步骤3中残留的杂波，并恢复降雨区域附近的点。

步骤5 数学形态学法恢复滤除的降雨目标。降雨目标区域内以及边界的点可能会被滤除，可以利用数学形态学的形态闭合来恢复缺失的降雨[10,23]。将结构单元设置为半径为5的平面圆盘。通过此过程，获得恢复降雨目标之后的掩模。

步骤6 图像填充恢复降雨目标。经过步骤5的处理会恢复大部分的降雨边界，但是降雨区域内部还会存在一些空洞。为了进一步恢复降雨目标，对步骤5得到的二值图像进行填充。当空洞封闭时，图像填充会将该空洞填充为周围背景的值。

下面从香农熵的角度阐述自适应阈值选取的原理。

3.2 阈值自适应选取

信息熵(香农熵)常被用来作为一个系统信息含量的量化指标，可以用来作为系统方程优化的目标或者参数选择的判据[24]。JS散度是一个基于信息熵的用于比较两个分布之间的相似性或差异性的参数[25]，其定义如下：

其中，P(X)和Q(X)是两个不同分布的归一化概率密度函数，0≤JS(P||Q)≤1,J S(P||Q)=0表示两个概率分布完全相同，JS(P||Q)=1表示两个概率分布完全不同[26]。在谱极化滤波中，X表示谱极化参量之一，即

杂波与无降雨情况下X的概率分布相似，降雨目标与无降雨情况下X的概率分布差异较大。利用这一特点，本文把无降雨情况下X的概率分布作为基准，分别衡量杂波、降雨目标与无降雨情况下X概率分布的差异。

为了防止单一组数据计算概率分布造成的特殊性和偶然性，本文利用多组无降雨情况下的数据来计算每个方位向上X的平均概率分布，在保持地杂波分布的情况下降低偶然出现的运动杂波的影响。

平均概率分布求解方法为：首先，按照方位角序列依次求解多组数据在每个方位向上X的概率分布；其次，根据多组数据的概率分布依次求得每个方位向上平均概率分布为

利用JS散度确定在方位角α上谱极化滤波的阈值。

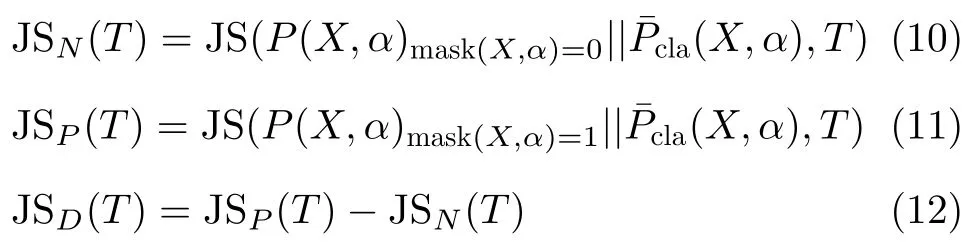
其中，m ask(X,α)=0 表示在方位角α上非降雨目标部分，JSN(T)表示非降雨目标部分与无降雨目标情况下X分布之间的散度；J SP(T)表示降雨目标部分与无降雨目标情况下X分布之间的散度。

图2为在方位角α上确定最优阈值的算法。该算法输入是X阈值的搜索范围[Tmin,Tmax]，此搜索范围由降雨目标在X上的分布确定。ΔT是阈值的步进值，考虑到计算效率和滤波效果，此步进值取(Tmax-Tmin)/100。在利用JS散度最大限度地提取降雨回波时，对于一个最优的阈值T使得J SN(T)较小，JSP(T) 较大，当J SD(T)达到最大值时的阈值T为最优的阈值(Topt)。求解步骤具体为：首先，根据输入的阈值求J SD(T)；其次，求J SD(T)的最大值点，对JSD(T)求导，如果在搜索范围内存在一个阈值T使得，那么此阈值即为J SD(T)的极大值点，取此阈值为最优的阈值；如果不存在使得的点，即在此方位角中没有降雨目标，为了更好地滤除非降雨目标，取Topt为J SD(T)的最大值点。

图2 阈值选取算法流程图Fig.2 Flow chart of the algorithm for threshold selection

4 sDR滤波及结果分析

4.1 雷达系统与杂波特性分析

将JS散度最优滤波阈值选取方法应用于AMsDR滤波器中，并与MsDR滤波器进行比较，使用IDRA雷达的数据对所提的滤波器进行性能验证。IDRA雷达是X波段高分辨极化-多普勒气象雷达。该雷达的测量模式为交替发射同时接收(Alternate Transmission and Simultaneous Reception,ATSR)模式，其具体参数如表1所示。

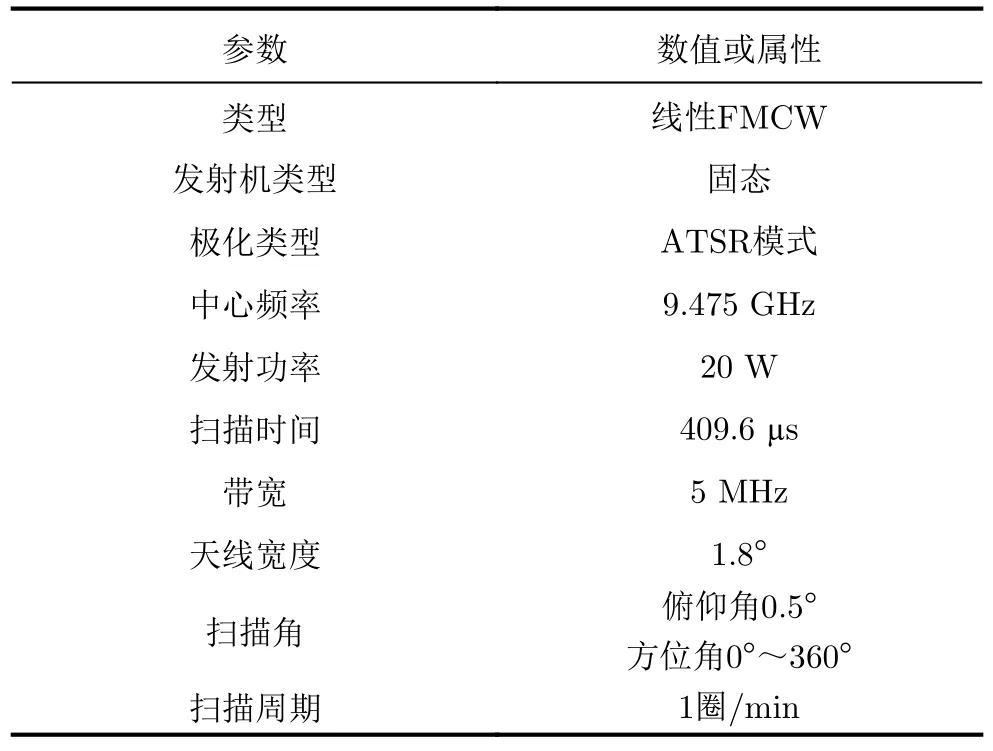
表1 IDRA雷达参数Tab.1 IDRA radar specifications

利用测量于2016年3月9日00:00—2016年3月13日12:00(UTC时间，每隔12小时测一组数据)的无降雨数据计算非降雨部分的平均概率分布。以2016年3月9日00:00的数据为例，其原始雷达PPI如图3(a)所示。使用测量于2017年4月26日00:00(UTC时间)含降雨的数据进行滤波性能测试，其原始雷达PPI如图3(b)所示。

使用如图3(b)所示的数据进行处理，其方位角为316.9°(图3(b)黑色虚线)时谱极化参量如图4所示。

图3 原始反射率Fig.3 Raw reflectivity

由图4(a)可见该方位向数据中除了含有气象目标外还包含带状杂波和地杂波。通过多个方位向数据的统计分析，地杂波主要集中在零多普勒处，位置相对固定。带状杂波主要有以下几个特点：(1)多普勒速度不为零；(2)在RD图上随机出现，带状杂波在不同方位向出现的位置都不相同；(3)带状杂波强度与降雨目标相当。带状杂波的这些特征增加了杂波抑制的难度[21]。

由图4(b)可见，降雨的 sZdr为正值。带状杂波的 sZdr时正时负，并且降雨与周围环境的sZdr差别不大。因此，使用 sZdr来区分降雨和杂波并不合适。大多数双极化雷达系统可测量得到谱共极化相关系数 sρco。大多数降雨目标的sρco非常接近于1，非降雨目标的 sρco远低于1。图4(c)表明，地杂波、带状杂波和降雨的sρco相 似。这意味着仅使用sρco不足以区分降雨，应该结合其他技术进一步去除这些杂波[20]。

由图4(d)可见，降雨与杂波以及噪声的 sDR值差异较大，这表明 sDR在抑制杂波方面具有较好的能力。对于没有交叉极化测量能力的双极化气象雷达，sDR是有效的滤波极化参量。

基于上述分析，本文选取s DR参数进行谱极化滤波。下面分别从RD和PPI的角度对AMsDR的性能进行说明。

4.2 谱极化滤波

4.2.1 滤波阈值确定

选取图4的数据，根据式(10)和式(11)计算JSP散度及 JSN散度和滤波阈值T之间的关系如图5(a)所示，根据式(12)计算 JSD散 度与滤波阈值T的关系如图5(b)所示，其中T=-9.6 是J SD的极值点。由图5可知，当阈值T在[-15，-9.6]区 间时，J SP散度增长较快，JSN散度增长较慢。说明随着阈值T的增加，保留的降雨目标变多，这一部分的分布特性与晴空条件下的分布特性差异变大；当阈值T在[-9.6,-5]区间时，情况相反。因此，在方位角为316.9°时取Topt=-9.6 dB。

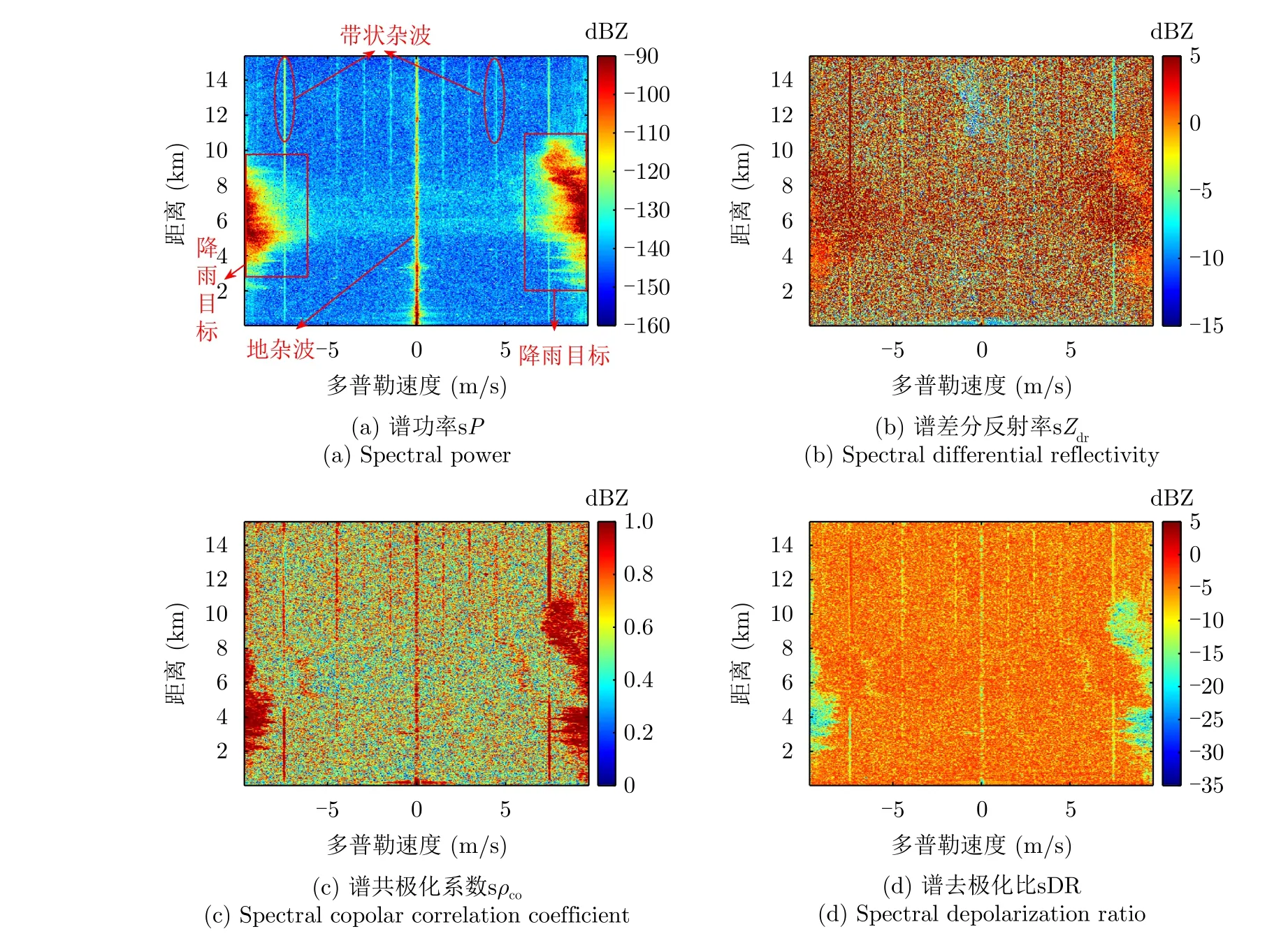
图4 IDRA雷达在方位角为316.9°时的谱极化参数Fig.4 The spectral polarimetric variables of IDRA radar at an azimuth angle of 316.9°

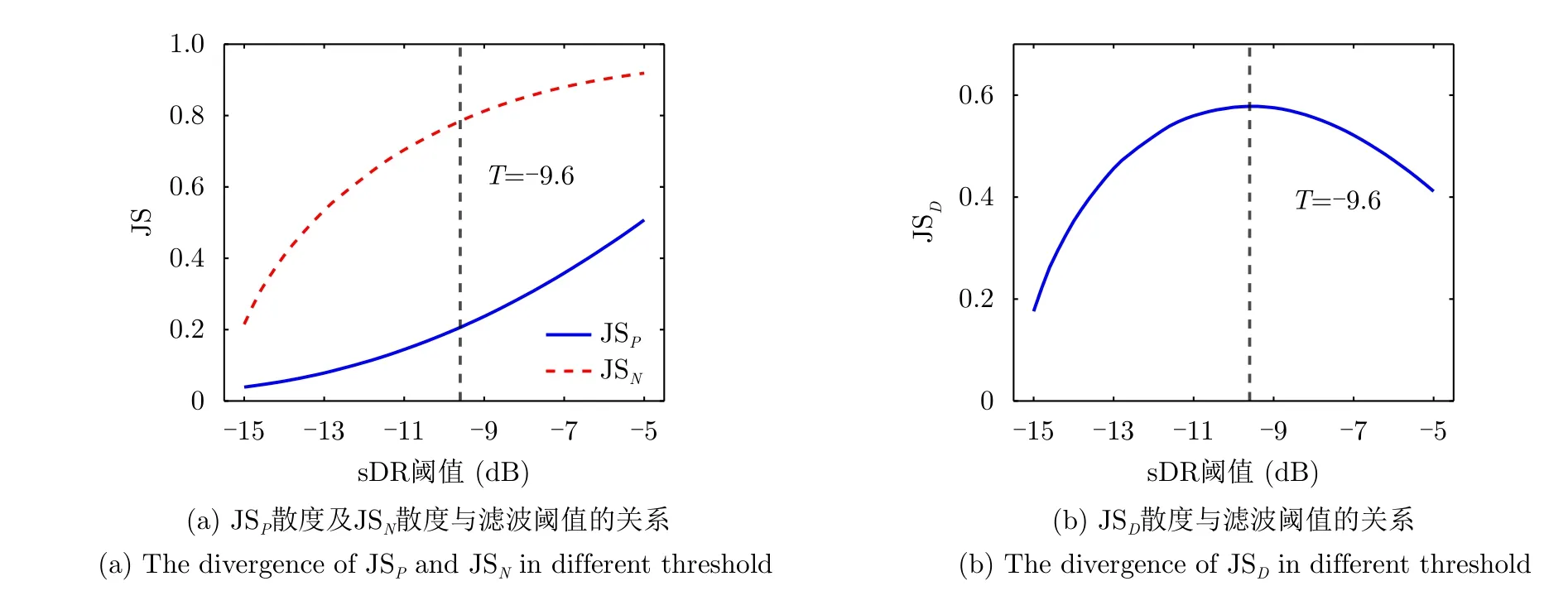
图5 JS散度与阈值T的关系Fig.5 Relationship between the JS divergence and the threshold T

4.2.2 谱极化滤波分析

选取图4的原始谱功率进行自适应谱极化滤波，得到图6(a)和图6(b)所示的结果。图6(a)是使用MsDR滤波器滤波后得到的结果，此时的滤波阈值为—10 dB，该阈值是根据降雨目标和杂波去除的比例[10,21]，并结合降雨和杂波的概率密度函数分布确定的[21,26]；图6(b)是使用本文提到的自适应阈值选取的算法，得到滤波阈值为—9.6 dB进行滤波的结果。两种滤波方法在方位角为344.7°时的对比如图6(c)和图6(d)所示，此时滤波阈值为—9.2 dB。

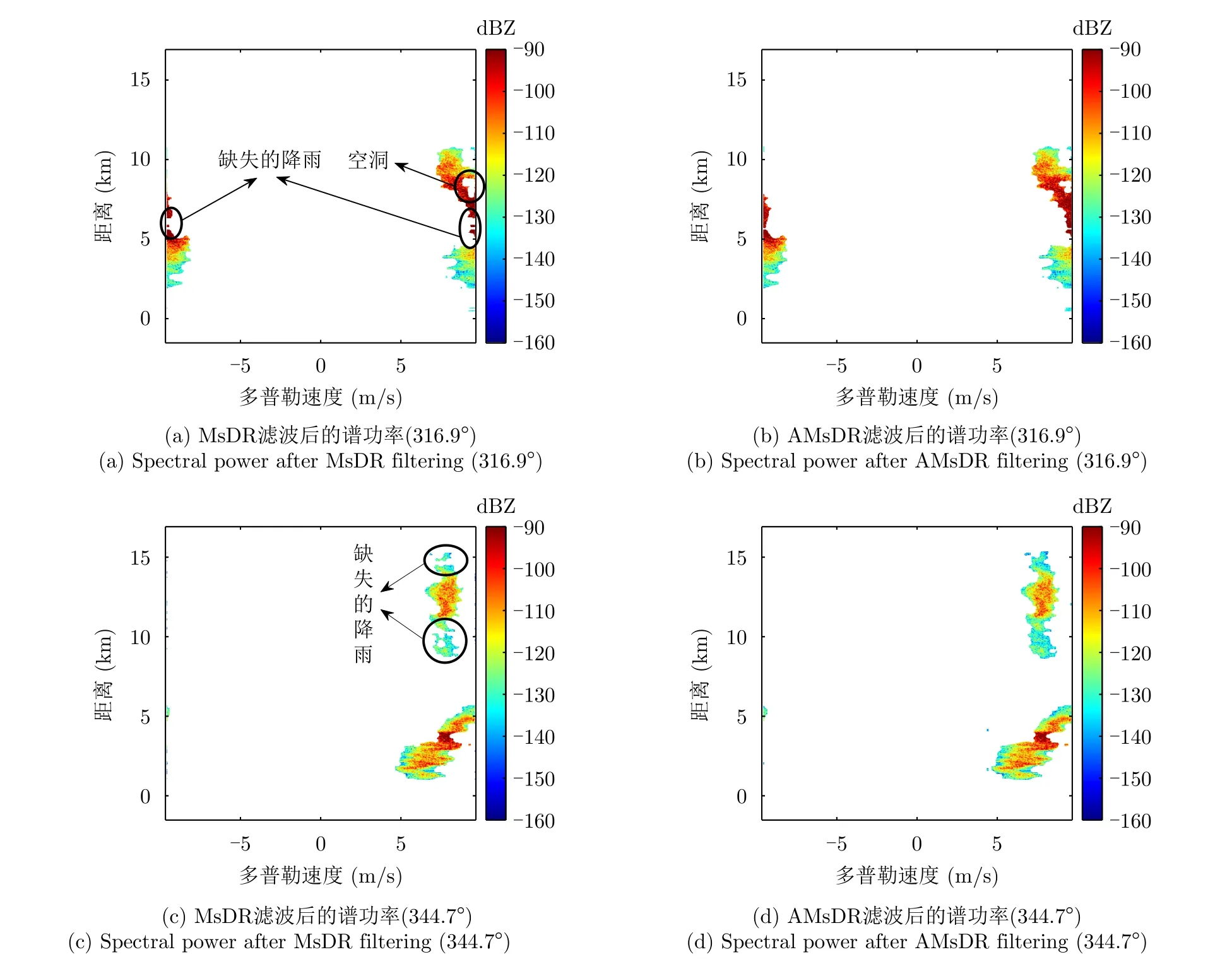
图6 滤波之后的谱功率Fig.6 Spectral power after filtering

对比图6(a)和图6(b)，两种滤波阈值都可以有效地去除与降雨目标分开较好的地杂波以及与降雨目标重叠的带状杂波。在5～8 km处，MsDR滤波会造成气象目标区域内部和边缘的降雨目标缺失(图中圆圈所示)，利用AMsDR方法滤波情况得到改善，但在7～8 km处也会存在一个较小的空洞。这里的空洞是由速度模糊造成的，速度模糊导致降雨区域不连续，图像填充算法无法将降雨目标填充。对比图6(c)和图6(d)，方位角为344.7°时AMsDR滤波方法在保留弱降雨目标方面效果优于MsDR。

4.3 PPI处理与结果分析

经过以上谱极化滤波的步骤，大部分的带状杂波会被滤除。利用降雨的空间连续性，本文在PPI维度滤除残留的杂波。此滤波步骤作用于谱极化滤波之后的PPI功率图，通过产生一个{ 0,1}的二值滤波掩模，使用谱极化滤波步骤4，利用式(5)和式(6)实现降雨目标的保留并进一步滤除杂波。

应用RD谱极化滤波以及PPI滤波处理后的雷达反射率在全扫描角度下的PPI显示结果，如图7所示。

图7(a)是利用MsDR滤波器处理的PPI结果，图7(b)是利用文中提出的AMsDR滤波方法以及PPI维滤波得到的PPI结果。从图中可以看出，利用MsDR滤波存在大量散点且降雨区域不连续。相比之下，本文的滤波方法散点较少且降雨区域较连续。

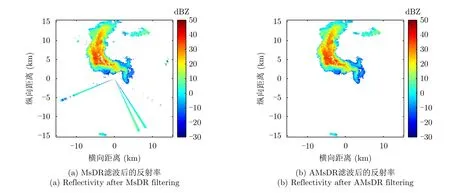
图7 滤波处理后的反射率Fig.7 Reflectivity after filtering

利用2016年3月4日00:00与2017年4月26日12:00(UTC时间)的数据对自适应滤波器的性能进行验证。经过MsDR以及AMsDR滤波之后的反射率因子如图8和图9所示。对比图8(b)与图8(c)以及图9(b)与图9(c)可知，无论是晴空还是有部分降雨，在滤除杂波和保留降雨方面，AMsDR滤波器的性能优于MsDR滤波器。

图8 2016年3月4日00:00 (UTC时间)的雷达数据不同处理后的反射率因子Fig.8 Reflectivity after different processing of the radar data at 00:00,4 March 2016 (UTC time)

图9 2017年4月26日12:00 (UTC时间)的雷达数据不同处理后的反射率因子Fig.9 Reflectivity after different processing of the radar data at 12:00,26 April 2017 (UTC time)

5 结论

针对双极化雷达中非气象回波的滤除问题，本文提出了一种AMsDR滤波方法。该方法根据气象目标和杂波在RD图上的谱极化特征和区域连通性的特性差异在保留气象目标的同时滤除杂波。首先根据径向扫描数据确定该径向滤波阈值，在RD图上生成一个二元掩模。基于面向对象的思想，将二元掩模标记为气象对象掩模和杂波对象掩模。然后利用数学形态学以及图像填充方法恢复降水，最终实现自适应谱极化滤波。本文对原始功率谱应用自适应滤波方法，可以更好地在保留气象目标的同时去除杂波和噪声。最后，通过实测气象雷达数据的杂波滤除结果验证了本文方法的有效性。结果表明，所提方法与MDsLDR滤波器相比具有更加广泛的应用，与固定阈值的MsDR滤波器相比有更好的杂波抑制与降雨保留性能。此外，该方法实现简单，计算复杂度较低。