考虑靶背自由面效应的中等厚度混凝土介质侵彻工程模型

刘志林,乔 良,徐 坤,王晓鸣,姚文进

(1.北京航天长征飞行器研究所,北京 100076;2.南京理工大学 智能弹药技术国防重点学科实验室,江苏 南京 210094)

弹丸侵彻混凝土或钢筋混凝土的研究一直是国内外钻地武器研究的重点和难点。由于混凝土材料比金属材料复杂得多,离散性大,研究困难,目前针对其侵彻能力的研究主要以实验手段总结归纳出用于工程计算的经验和半经验公式为主。随着弹药武器毁伤评估领域的蓬勃发展,动能侵彻武器的侵彻能力快速评估模型是评估系统中的重要研究内容。

陈小伟等根据动态空腔膨胀理论和冲塞机理,建立了包括开坑段、隧道稳定侵彻段和剪切冲塞出靶段的三阶段侵彻混凝土介质计算模型。王明洋等和葛涛等在水动模型的基础上,认为靶体裂纹扩展到背面时开始不稳定增长,将此刻作为贯穿开始时刻,并利用裂纹增长的耗能机制求得贯穿块的厚度。其假设贯穿块与弹丸一起运动,直到弹丸与冲塞块的以相同速度共同作用时,冲塞块对弹丸的阻力也就降至零,以此物理过程建立弹丸剩余速度计算模型。刘志林等研究靶板厚度对侵彻影响时发现,弹丸速度相对较低时会发生混凝土冲塞块整体飞出,余速较大时弹丸都是快于冲塞块形成之前飞出混凝土出靶面。

本文采用冲塞块作为出靶模型的基本假定,同时考虑自由表面对弹丸贯穿的影响,并利用有限空腔膨胀理论构造阻力的衰减函数,修正空腔膨胀理论推导出的阻力函数,模拟弹丸贯穿效应。

1 侵彻模型

1.1 考虑自由面效应的侵彻阻力模型

弹丸侵彻有限厚度靶时,由于靶体材料在弹丸扩展方向的厚度是有限的,侵彻阻力无法用半无限空腔膨胀理论推导,需要考虑靶体自由表面的影响。存在自由表面效应时,空腔膨胀理论模型需要引入自由面边界。由于当响应区的边界扩展到自由表面时,无法再继续扩展,因此，可把自由表面视为新的响应区边界。

图1 有限空腔膨胀响应分区

WARREN等在研究卵形弹丸侵彻半无限靶时根据有限球形空腔膨胀模型推导出了自由表面效应修正函数,并成功用于弹丸开坑阶段的空腔膨胀阻力修正。如图1所示,当弹体表面离靶体自由面较远时,会出现弹性和塑性两个响应区。而当弹体表面离靶自由表面较近时,弹性区消失,只存在塑性区。

根据有限空腔分区假设,对空腔膨胀理论的控制方法进行求解,从而获得空腔表面压力与膨胀速度的关系。球对称欧拉坐标系下的动量和质量守恒方程分别为

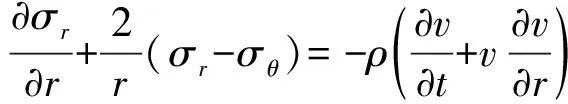
(1)

(2)

式中:和为径向和环向应力;和为混凝土介质变形前后密度;和为质点速度和位移。

代入Mohr-Coulomb屈服准则,根据弹性与塑性边界径向应力连续的条件,可推导出空腔表面的应力公式:

(3)

式中:、为混凝土Mohr-Coulomb屈服准则中定义压力相关混凝土剪切强度材料参数;、、为分区界面径向坐标;为混凝土弹性模型量;=6(3+2)。

从空腔膨胀导出的空腔表面应力表达式可以发现,应力大小与自由面位置相关。基于这一特性构造与自由面位置相关的阻力衰减函数:

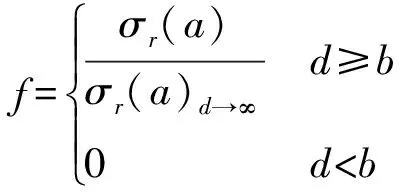
(4)

图2给出了不同空腔膨胀速度下的衰减函数值与自由面边界位置关系图,当自由面无穷远时,衰减函数值为1;当弹性区边界与塑性区边界重合时,衰减函数值为0。膨胀速度越高,自由面的影响范围越大,速度大于400 m/s后影响不随速度而变化。基于构造的衰减函数对弹丸侵彻混凝土靶受自由面影响的阻力函数进行修正,弹丸的阻力方程可以写成:

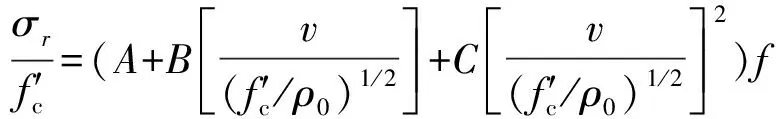
(5)

式中:为空腔表面径向应力;′为混凝土无侧限抗压强度;,,为空腔膨胀理论中侵彻阻力系数,系数求解过程见文献[10];为空腔膨胀速度。

图2 不同膨胀速度下衰减函数曲线

文献[10]采用基于盖帽混凝土模型推导了半无限侵彻阻力,并通过速度在800～1 400 m/s范围内的弹丸侵彻半无限混凝土靶的试验进行了验证。本文采用其中的侵彻阻力作为半无限侵彻阻力模型。

1.2 冲塞判据

文献[8]表明,当弹丸余速较低时,会出现冲塞现象,会有大面积整体混凝土块向外崩落。为了能够在模型中考虑这一特性,在弹丸侵彻过程中,假设当弹丸的侵彻阻力等于冲塞块断裂时刻剪切面所需合力时,冲塞发生。其判据可以写成:

==cos()

(6)

式中:为混凝土纯剪失效强度;为冲塞块侧向面积;为冲塞块半锥角。

2 计算与分析

文献[8]开展了靶板厚度对侵彻影响研究试验,试验中以105 mm口径火炮为发射平台,采用次口径发射技术,试验中弹丸直径为60 mm,战斗部设计质量约为4.15 kg。弹丸速度有高速和低速两种,靶板有6个厚度,具体试验参数见表1,表中为靶板厚度,为弹丸质量,、分别为弹丸撞击速度和剩余速度。

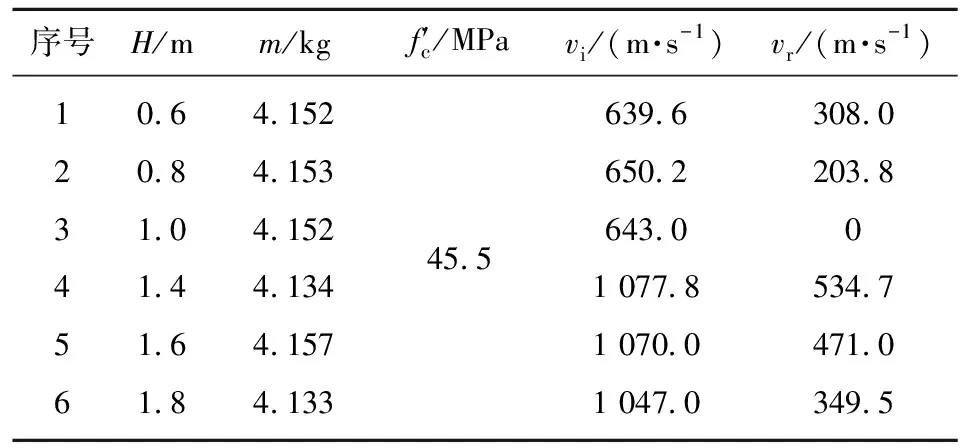
表1 文献[8]试验参数

文献[10]给出了采用侵彻阻力计算侵彻深度的方法,以时间为步长,通过程序迭代牛顿第二运动方程,得到侵彻深度以及弹丸的其它时空物理量。本文以此方法,考虑自由面效应的侵彻阻力,建立了侵彻模型,并对试验工况进行了计算,结果见表2。

表2 计算结果与试验和仿真结果对比

表2给出了本文模型计算结果与试验结果以及误差值。结果表明本文计算结果与试验吻合良好,剩余速度误差除了试验1(误差22.1%)以外均小于10%;与仿真剩余速度结果发现,本文计算误差不超过7.7%,对比结果表明模型计算剩余速度结果精度满足威力快速评估要求。

针对试验工况,通过模型计算的弹丸过载与弹丸位移曲线如图3所示。弹丸在两种速度下的侵彻过载峰值重合,过载随着侵彻深度呈线性减小的趋势,在接近靶后自由面后开始急速降低,直至弹丸穿出靶体。靶板厚度为1.0 m的试验工况的计算结果显示破坏模式为冲塞破坏,与试验现象一致。这表明了本文模型不仅可以预测极限贯穿厚度,还可以预测临界冲塞工况,验证了本文模型的可靠性。

图3 侵彻过载计算结果

图4给出了模型计算过载与文献[8]中的仿真过载对比结果。结果表明本文计算模型与仿真过载趋势吻合,两种速度下的峰值过载误差小于4.4%,剩余速度误差小于7.7%。

图4 侵彻过载模型计算结果与仿真结果对比

图5给出了NDRC经验公式和本文模型预测试验工况下的贯穿临界厚度。结果显示NDRC公式在同一撞击速度下的预测厚度偏小,随着速度的增加,偏差值越大。而本文模型预测结果与试验更符合,且NDRC公式不能预测速度大于800 m/s的试验工况,表明本文模型有更高的精度和更广的适用范围。

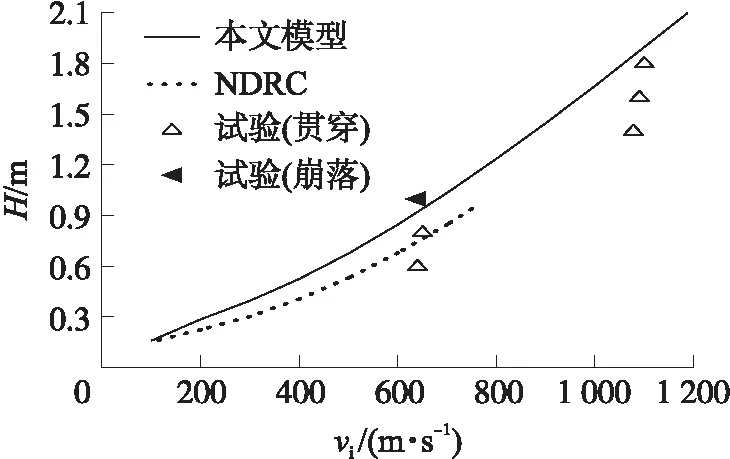
图5 模型临界贯穿厚度预测与NDRC经验公式对比

3 结束语

本文在半无限侵彻模型的阻力基础上,引入靶背自由面衰减函数的影响并考虑了冲塞剪切的破坏模式,建立了考虑自由面效应的侵彻和贯穿模型。通过对比试验结果和仿真结果发现:本文模型计算结果与试验余速误差小于22.1%;本文模型计算结果与仿真的过载误差小于4.4%;本文模型计算结果较NDRC经验公式预测结果更接近试验,NDRC预测临界贯穿厚度偏小。与试验和经验公式对比再一次验证了本文模型计算结果的可靠性,是一种可用于评估混凝土抗贯穿能力的研究手段。