基于自适应鲁棒控制的坦克俯仰系统建模与仿真

曾子健,杨国来,龙义强,孙全兆,王丽群

(1.南京理工大学 机械工程学院,江苏 南京 210094;2.四川临港五洲工程设计有限公司,四川 泸州 646000)

坦克俯仰系统是坦克炮控系统的重要组成部分。坦克行进过程中,受路面等外部激励的影响,身管会发生垂向振动,从而偏离预期位置,降低坦克行进间的射击精度,因此需要俯仰系统针对偏差予以实时修正。

近年来,针对坦克俯仰系统的研究逐渐深入,在多体系统建模和控制算法设计等方面取得了诸多成果。史力晨等针对坦克底盘-火炮系统行驶时的振动问题进行了动力学建模与分析,建立了坦克-火炮系统动力学微分方程,并对车体振动对火炮运动的影响进行了仿真分析。郝丙飞等针对坦克底盘-火炮系统行驶过程中高低向俯仰角振动问题建立了坦克底盘及火炮的多体模型,在实车试验验证了模型合理性的基础上进行了仿真分析,结果表明火炮俯仰角振动随着路面不平度增大和车速提高而变大。然而上述研究并未考虑坦克俯仰控制系统的作用。

随着现代控制理论不断发展,越来越多的控制方法被应用于俯仰控制系统,自适应鲁棒控制便是其一。自适应鲁棒控制理论经过了严格的数学论证,既结合了自适应控制和鲁棒控制的优点,同时又避免了各自的缺陷。对于同时具有参数不确定性和不确定性非线性的复杂系统,该控制策略能够通过自适应算法估计系统的不确定性参数以提高控制精度,同时利用鲁棒控制来避免因自适应控制而导致的不稳定问题,最终使得自适应鲁棒控制具有更好的跟踪稳定性能。然而,坦克俯仰系统作为一个复杂的机电耦合系统,对其控制方法的研究需以坦克多体系统为基础。

本文利用RecurDyn软件建立坦克行进间多体系统动力学模型,同时建立基于干扰观测器的俯仰系统自适应鲁棒控制模型,并通过联合仿真验证该控制器作用下火炮的跟踪和稳定性能。

1 坦克多体动力学建模

1.1 坦克多体系统动力学建模

坦克是一个复杂的机械系统,在对其进行多体系统动力学建模时需进行必要的简化。本文将坦克简化为两个部分,分别为底盘部分和火力部分,二者以上下座圈相连接。底盘部分主要由履带和车体等组成;火力部分则由身管、摇架、炮尾以及炮塔等组成,各构件以合适的铰接方式相连接。根据上述简化,在软件RecurDyn中建立坦克动力学模型。

1.2 路面不平度建模

坦克行进过程中,由路面激励引起的车体振动是炮口振动的主要影响因素,因此有必要建立准确的路面不平度模型。路面不平度是指道路表面相对于理想平面的偏离,它描述了随机路面下车辆的振动输入。根据国标规定,路面不平度功率谱密度表达式如下:

(1)

式中:∈[,]为空间频率,为参考空间频率。()为路面不平度系数,为频率指数。

本文利用谐波叠加法对路面进行重构,通过改变路面不平度系数建立了长200 m,宽10 m的不同等级路面模型。

1.3 模型初步验证

将上述路面模型利用节点缝合法生成动力学软件可读的路面文件并导入坦克多体系统动力学模型,结果如图1所示。

图1 坦克行进间多体系统动力学模型

为验证所建立模型的准确性,将仿真结果与文献[11]的试验结果进行对比分析。根据试验信息,对模型分别设定以14 km/h、21 km/h和31 km/h三档速度在B级路面行驶,同时采集第一负重轮上方车体垂向振动加速度信号,经计算得到加速度功率谱密度最大峰值频率。表1为仿真值与试验值对比。

表1 仿真结果对比

对比结果表明,第一负重轮上方车体垂向振动加速度信号功率谱密度最大峰值频率的仿真值与试验值较为接近。三档不同车速最大峰值频率的仿真误差分别为-14%、-13.3%和-14.3%,这表明所建模型具有一定的合理性。此外,随着车速的提高,最大峰值频率仿真值的变化规律与试验值变化规律基本一致,说明模型能够较好的反应路面激励变化对坦克振动的影响,这也增加了模型的可信度。考虑到建模时忽略了各结构的弹性变形及接触碰撞,可认为模型误差在合理范围内。

综上所述,建立的坦克行进间多体系统动力学模型与实际情况较为接近,具有一定的合理性和可信度,能够作为进一步开展相关研究的基础。

2 俯仰系统机电一体化建模

2.1 俯仰系统动力学分析

坦克俯仰系统由控制系统和执行机构组成,其中执行机构包括永磁同步电机与丝杠。在坦克行进过程中,车体受路面激励而发生俯仰运动。此时控制系统控制电机转动,经传动机构作用于摇架,使其带动身管绕耳轴反向转动以抵消车体振动的影响,从而保持身管稳定。为方便分析,将摇架和炮尾视为与身管一体(以下统称身管),建立俯仰系统动力学模型,如图2所示。图中,、、和分别为耳轴作用点、身管质心、丝杠作用点和车体质心;为身管相对于惯性系俯仰角;为车体相对于惯性系俯仰角;为丝杠对应顶角角度,当身管处于水平位置时,=。

图2 俯仰系统动力学模型

根据系统受力分析,可得到身管绕耳轴的转动方程:

(2)

式中:为身管绕耳轴作用点的转动惯量;为丝杠作用力矩;为重力矩。

丝杠作用力由电机输出转矩经丝杠得到,同时与丝杠导程和传动效率有关,即:

(3)

因此,式(2)可以写成:

(4)

此外,根据传动装置以及图中几何关系,易得出电机输出角度与身管俯仰角的关系:

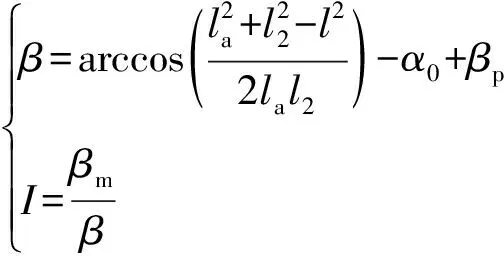
(5)

式中:为传动比。

2.2 俯仰系统数学模型

本文以表贴式永磁同步电机(PMSM)为俯仰系统执行机构,采用=0控制,其在坐标系下的数学模型为

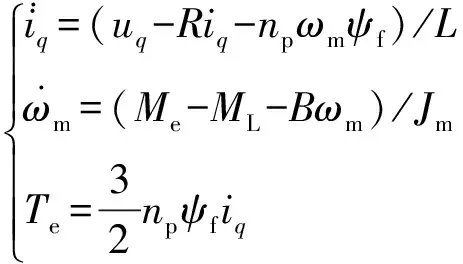
(6)

式中:、为轴电流、电压;、、、、、和为电机电阻、电感、输出轴转动惯量、粘滞系数、磁链、极对数和转速;和为电机输出转矩和扰动力矩。

对式(6)进行拉氏变换并考虑俯仰系统传动比,可得到如图3所示的基于三环控制的俯仰系统数学模型。图中,为三环控制器,=+,为系统负载侧转动惯量折算到电机侧的转动惯量。

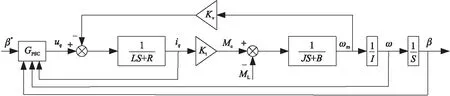
图3 俯仰系统数学模型

2.3 自适应鲁棒控制器设计

本文基于三环控制设计坦克俯仰控制系统。由于电流环反应速度快且跟踪效果较好,因此可忽略电流环的影响。此外,综合考虑速度环和位置环以设计自适应鲁棒控制器。

根据式(6)的运动方程可得:

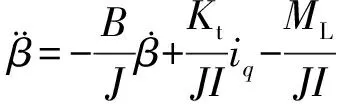
(7)

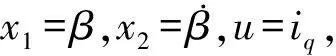
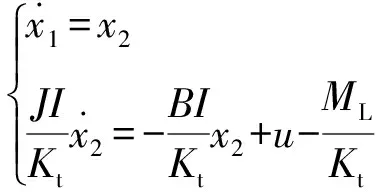
(8)

(9)

定义误差变量为

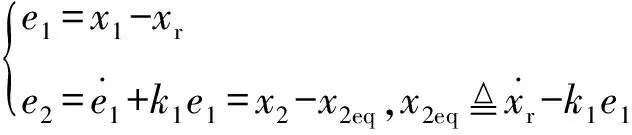
(10)

式中:为俯仰系统角度误差,为期望角度,为正反馈增益。

结合式(9)可得:

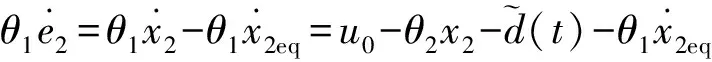
(11)

为使趋于零,对控制器进行以下设计:

(12)

(13)

式中:>0为正定的对角矩阵,为参数自适应函数,这里取=e。为使自适应率稳定,对参数自适应不连续映射进行如下定义:

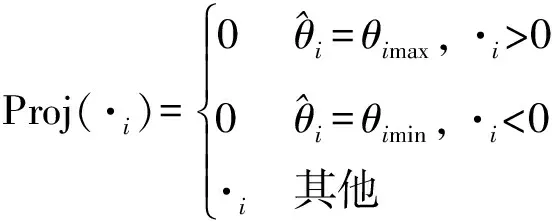
(14)

对进行设计以稳定系统。将式(12)代入式(11),得:

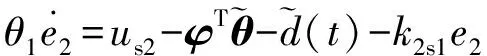
(15)

根据式(13),需满足如下镇定条件:

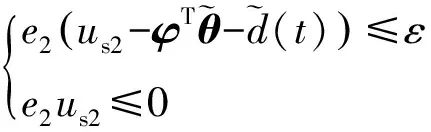
(16)

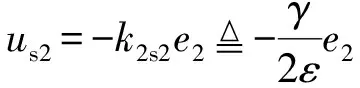
(17)

至此完成了自适应鲁棒控制器设计:

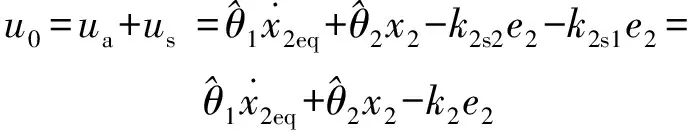
(18)

2.4 干扰观测器设计

取炮口角速度和扰动力矩矩常值分量为状态变量,电机输出力矩为输入,结合式(7)可写出状态空间方程:

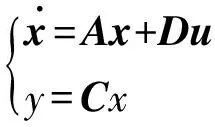
(19)

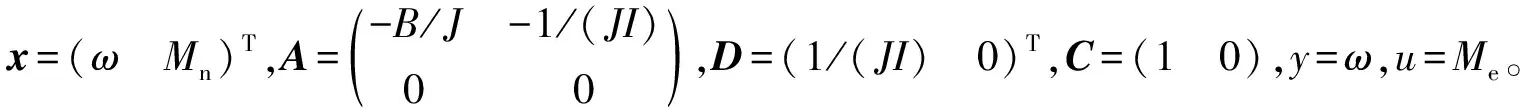
根据现代控制理论易知式(19)完全可观,其全维状态观测器动态方程为

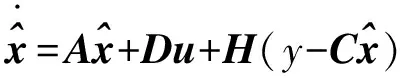
(20)

式中:=()。

设观测器的期望极点为{},则其希望特征多项式为

()=(-)(-)

(21)

根据式(19),其对偶系统的特征多项式为

4.规范设计实验流程和实验方案。设计和实施实验，必须有环环相扣的规范性实验流程和实验方案，任何环节出现差错，都会导致实验结果的偏差甚至致命的错误和失败。每一个实验项目的流程和方案都必须符合该实验的特殊要求。实验的过程是任何环节都不能允许出现差错的。

(22)

因此,根据式(21)和式(22)可得:

(23)

将式(23)代入式(20)可得干扰状态观测器为

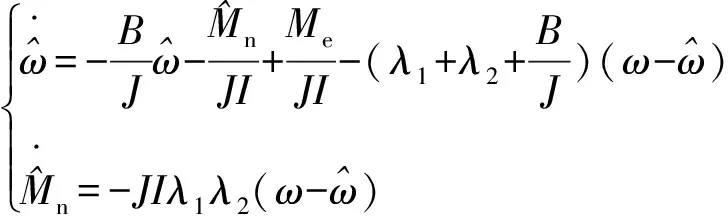
(24)

结合式(18)和式(24),可得基于干扰观测器的自适应鲁棒控制器:

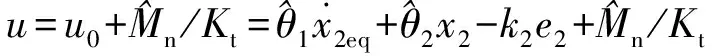
(25)

2.5 稳定性分析

完成自适应鲁棒控制器及干扰观测器的设计工作后,本节将分别对其进行稳定性分析。

对于23节设计的自适应鲁棒控制器,满足如下情况:

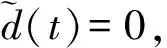
证明:对于情况1,选取如下Lyapunov函数:

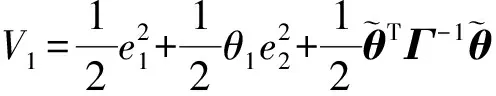
(26)

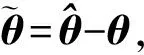
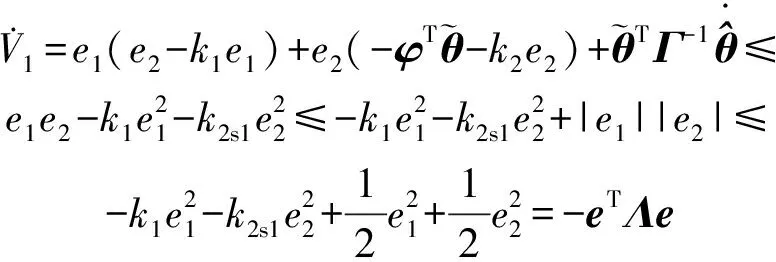
(27)

进一步的,可以得到:

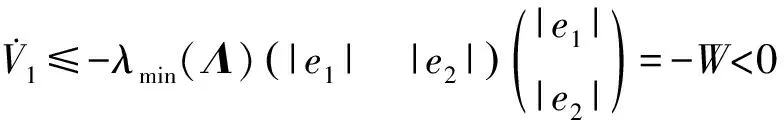
(28)

式中:为正定对称矩阵的最小特征值;为一正函数。至此情况(1)得证。

对于更一般的情况2,选取如下Lyapunov函数:

(29)

证明过程与情况1类似,这里不再赘述。

对于24节设计的基于干扰观测器的自适应鲁棒控制器,选取如下Lyapunov函数:

(30)

证明过程与情况1类似,这里不再赘述。

3 联合仿真

利用RecurDyn的接口模块与控制器进行联合仿真,验证坦克以20 km/h车速行驶在不同路面条件下控制器的控制效果。火炮稳定精度是衡量控制器性能的重要指标,其为坦克行驶时炮口摆动振幅的算术平均值:

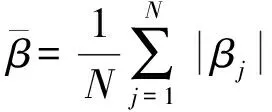
(31)

式中:为总的采样点数,为每个采样点的炮口俯仰角度。

仿真时长为10 s,由于坦克加速时存在较大振动,故采用4 s后数据进行分析。选用的永磁同步电机参数如下:电阻=0.4 Ω,电感=21.24 mH,转动惯量=0.002 15 kg·m,粘滞摩擦系数=1.43×10N·m/(rad·s),转矩系数=0.195 N·m/A,反电势系数=0.197 V/(rad·s)。

3.1 阶跃响应性能分析

图4为D级路面下,自适应鲁棒控制器和PID控制器的阶跃响应特性曲线。由图4可以看出,在4 s时给定一个200 mrad的阶跃信号后,二者均在4.6 s左右达到稳定状态。但是,自适应鲁棒控制器能够更快地对阶跃信号产生响应,且在接近目标角度时更加平滑,不会产生超调。相反的,PID控制器在达到目标角度时则会产生超调和振荡。因此,在阶跃响应方面自适应鲁棒控制器具有更好的控制性能。

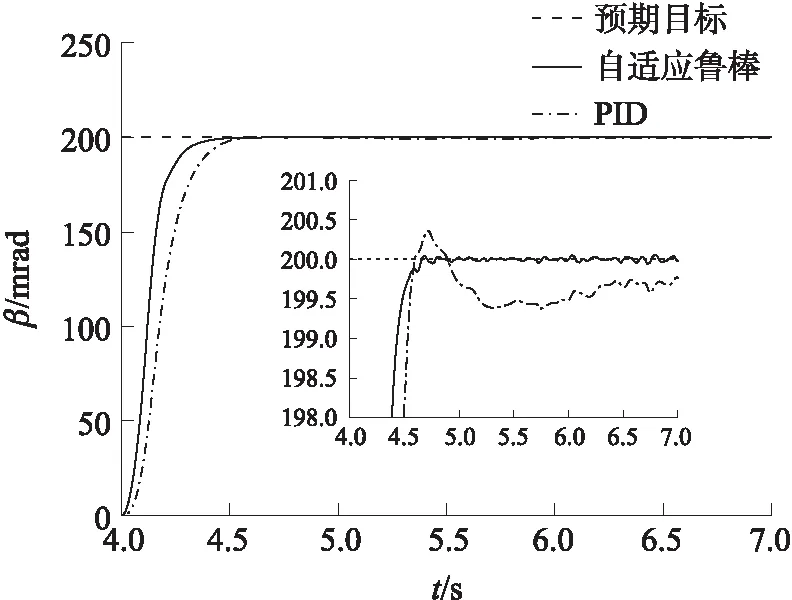
图4 阶跃响应曲线图

3.2 瞄准稳定性能分析

图5为不同路面等级条件下,自适应鲁棒控制器和PID控制器的稳定精度特性曲线。结合表2可以看出,在D、E、F 3种等级路面条件下,自适应鲁棒控制器的稳定精度相较于PID控制器分别提高了53%、72%和65%,这说明自适应鲁棒控制器具有更好的稳定性能。

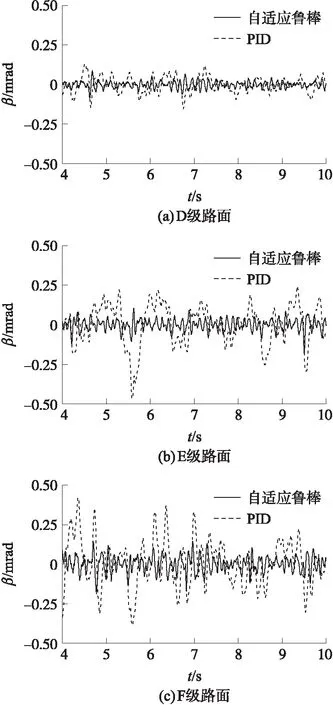
图5 稳定精度曲线图

表2 不同等级路面稳定精度

在D级路面条件下,自适应鲁棒控制器和PID控制器的稳定精度分别为0.018 mrad和0.038 mrad。然而随着路况变差,PID控制器的控制效果显著下降。在F级路面条件下,PID控制器的稳定精度为0.118 mrad,降低了0.08 mrad,而自适应鲁棒控制器的控制精度仍有0.041 mrad,仅降低了0.028 mrad。这说明自适应鲁棒控制器具有更强的鲁棒性和抗干扰能力。

4 结束语

本文利用RecurDyn软件建立了坦克多体动力学模型,将其仿真结果与试验进行对比,验证了模型的合理性。对以永磁同步电机为执行机构的俯仰系统进行了动力学建模分析,并以此建立了俯仰系统的数学模型。在此基础上,设计了基于干扰观测器的俯仰位置伺服系统自适应鲁棒控制器,并建立了俯仰系统控制模型。最后利用接口模块实现了坦克俯仰系统的联合仿真。

研究结果表明,相较于传统的PID控制,本文设计的俯仰控制系统拥有更好的阶跃响应性能和稳定性能。同时,在受到外部激励的影响时具有较强的鲁棒性和抗干扰能力。

本文在建立坦克行进间多体动力学模型时并未考虑身管柔性的影响,相对于实际情况仍有进一步完善的空间,这将是今后的工作之一。