修正Kadomtsev‐Petviashvili 方程的分解及其孤子解

李 权，扎其劳

（1.河套学院 数学与计算机系，内蒙古 巴彦淖尔 015008；2.内蒙古师范大学 数学科学学院，内蒙古 呼和浩特 010022；3.内蒙古自治区应用数学中心，内蒙古 呼和浩特 010022）

0 引言

众所周知，求解高维孤子方程难度很大［1‐2］。在过去的三十年里，许多研究学者致力于将高维孤子方程分解为几个已知的（1+1）维孤子方程，这些可以通过引入变量约束［1-3］的途径来处理，因此高维方程的解可以由相应的（1+1）维方程的解来表示。事实上，有许多方法可以获得（1+1）维孤子方程的精确解，如逆散射变换、Hirota 双线性方法、Bäcklund 和Darboux 变换、代数几何方法等，其中，Darboux 变换是获得某些孤子方程精确解的最有效的方法之一。1984 年，Neugebauer 和Meinel［4］给出一种系统的方法来直接构造AKNS系统的N重Darboux 变换。之后，该方法已被许多研究学者应用于寻找多孤子解。

本文将（2+1）维修正Kadomtsev‐Petvishivili（mKP）方程［1，5］

成功分解为Kaup‐Newell（KN）系统的前两个非平凡孤子方程组

约束条件为

式（4）和方程（2）~（3）满足方程（1），其中∂∂-1=∂-1∂=1(∂= ∂∂x)。如果利用方程（2）和（3）解出(u，v)，那么由约束条件（4）就能给出mKP 方程（1）的相应解。mKP 方程（1）是mKdV 方程的二维推广，被广泛研究［3-8］。

本文讨论KN 系统的N重Darboux 变换和mKP 方程（1）的多孤子解，目前相关内容研究较少。首先建立方程（1）与方程（2）~（3）之间的联系，然后根据Neugebauer 思想，通过KN 谱问题的规范变换，导出方程（2）~（3）的一个新的N重Darboux 变换［6-8］。最后，借助N重Darboux 变换和分解，得到mKP 方程（1）的多孤子解。

根据式（4）与方程（2）~（3），直接计算可得

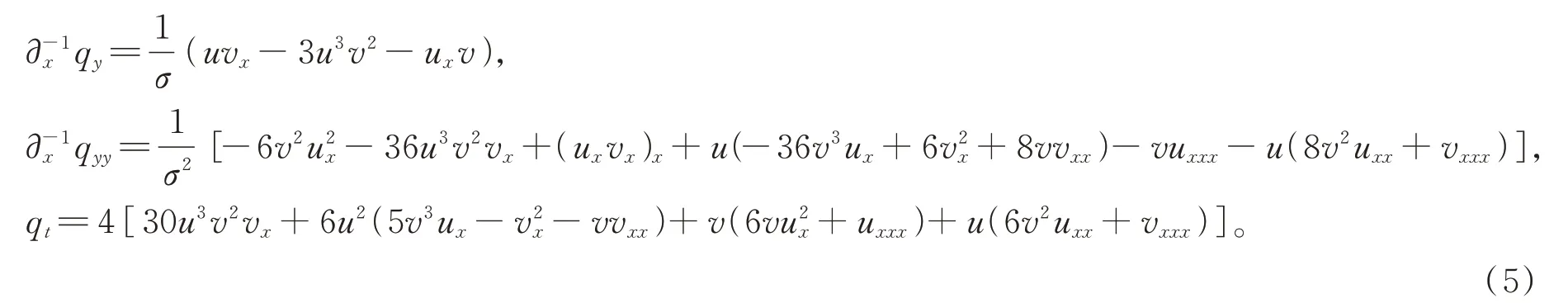
将式（4）~（5）代入方程（1），通过计算机代数系统Maple 或Mathematica，得到（4）满足（1）的结论。

方程（2）~（3）与Kaup‐Newell 谱问题

有密切相关，KN 谱问题（6）与AKNS 谱问题是规范等价。通过计算相容性条件Uy-V(4)x+UV4-V(4)U=0 和Ut-V(6)x+UV(6)-V(6)U=0，可分别得到方程组（2）和（3）。

1 N 重Darboux 变换

构造KN 谱问题［6］的Darboux 变换。设ϕ=(ϕ1，ϕ2)T和ψ=(ψ1，ψ2)T是谱问题（6）~（8）的两个基本解，用(φ，ψ)定义Darboux 矩阵

其 中关于x，y和t的函数，A2k，B2K-1，C2k-1和D2k由线性方程组

给出，其中

适 当 选 择 参 数λj和rj(λi≠λj，ri≠rj，i≠j) 使 得 方 程（10）和（11）的 系 数 行 列 式 非 零，此 时A2k，B2k-1，C2k-1和D2k(1 ≤k≤N)由方程（10）和（11）唯一确定。等式（9）表明detT(λ)是λ 的4N次多项式，且detT(λj)=A(λj)D(λj)-B(λj)C(λj)。另 一 方 面，由 方 程（10）和（11）有A(λj)=-δj B(λj)，C(λj)=-δj D(λj)。因此，有detT(λj)=0。这意味着λj(1 ≤j≤2N)是T(λ)的2N个根，则是

其中γ与λ无关。

KN 谱问题（6）的Darboux 变换实际上是一个规范变换

类似于文献［6］中的证明，给出如下命题。

命题1由谱问题（15）~（17）确定的矩阵具有相同的形式，即

由旧位势u和v到新位势-u和-v的变换公式为

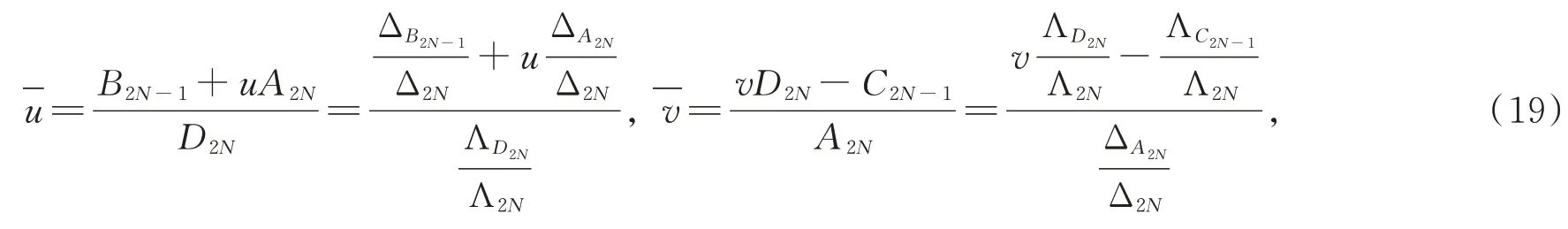
其中Δ2N和Λ2N是方程（10）和（11）的系数行列式，即

ΔA2N，ΔB2N-1分别由ΔN-1的第(2N-1) 列、第2N列替换为(-α，-α，…，-α)T而来，ΔD2N，ΔC2N-1分别由Λ2N的第(2N-1)列、第2N列替换为(-βδ1，-βδ2，…，-βδ2N)T而来。

根据命题1，很容易看出方程（15）和（16）也是（1+1）维孤子方程组（2）的Lax 对，方程（15）和（17）是（1+1）维孤子方程组（3）的Lax 对，变换（18）通常被称为（1+1）维孤子方程组（2）和（3）的Darboux 变换。

命题2设(u，v)是（1+1）维孤子方程组（2）和（3）的解，那么由Darboux 变换（19）确定的函数和是方程组（2）和（3）的另一个解，且函数

是mKP 方程（1）的一个新解。

2 Darboux 变换的应用

将应用Darboux 变换给出（2+1）维mKP 方程（1）的多孤子解。选择平凡解u0=v0=0，Lax 对（6）~（8）对应的相容基本解可以写成

将式（19）和（24）代入（22），得到k‐孤子解(1 ≤k≤N)的一个统一的显式公式，因此很容易得到方程（1）的N‐孤子解。为了简单起见，将讨论两种特殊情形N=1 和N=2。

情形1（N=1）。当λj，rj(j=1)时，式（22）是mKP 方程（1）的一个精确解

情形2（N=2）。当λj，rj(j=1，2，3，4) 时，式（22）是mKP 方程（1）的另一个精确解

其中

δj=(j=1，2，3，4)在式（24）中确定。选择适当的参数（如λ2=iλ1和λ4=iλ3），解（27）为双孤子解。图1（b）为该解的三维图。

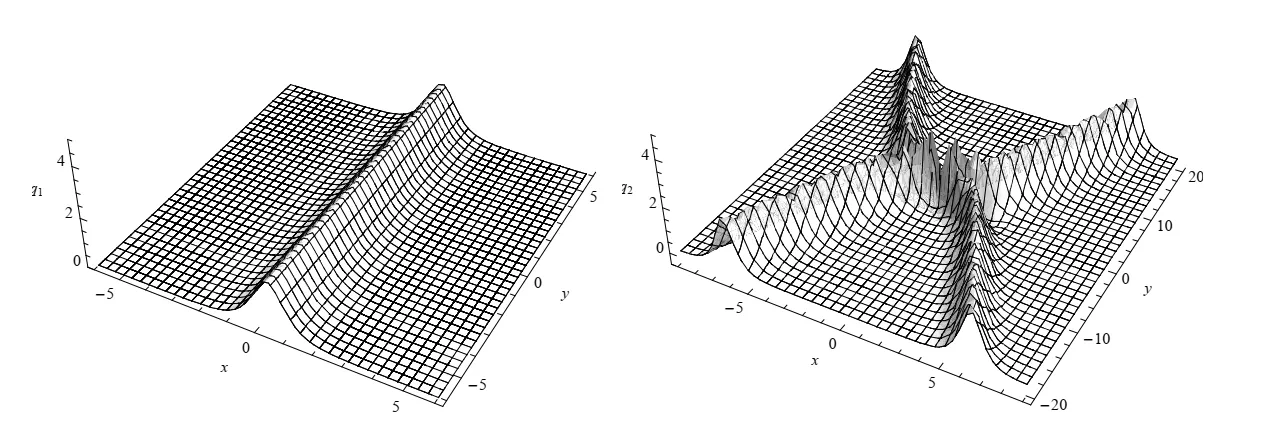
图1 （a）单孤子解（26）取参数μ1=1，r1=0.1，r2=0.2，σ=-1，t=0；（b）双孤子解（27）取参数λ1=1，λ2=i，λ3=1.1，λ4=i1.1，r4=-r3=r2=-r1=0.1，σ=-1，t=0Fig.1 （a）The single soliton solution（26）with μ1=1，r1=0.1，r2=0.2，σ=-1，t=0；（b）The double soliton solution（27）with λ1=1，λ2=i，λ3=1.1，λ4=i1.1，r4=-r3=r2=-r1=0.1，σ=-1，t=0

重复上述步骤，可得mKP 方程（1）的一系列多孤子解。

3 结论

目前，诸多（1+1）维方程的求解方法被广泛提出和使用，但相比于此，（2+1）维方程的求解方法不是很普遍。本文成功地将（2+1）维mKP 方程分解成两个（1+1）维KN 孤子方程组，并应用这两个（1+1）维孤子方程组的N重Darboux 变换获得了（2+1）维mKP 方程的孤子解。