管壳引脚的低应力玻璃封接

蒋玉齐，周超杰

（无锡中微高科电子有限公司，江苏 无锡 214035）

0 引言

金属封装采用金属作为壳体或底座，芯片直接或通过基板安装在外壳或底座上，引线穿过金属壳体或底座时大多采用玻璃-金属气密封接技术。它被广泛地用于混合电路的封装，也适合于射频、微波、光电、声表面波和大功率器件；在许多领域，尤其是在电源、航空航天、汽车电子、医疗和照明灯领域中得到了广泛的应用[1-2]。

玻璃与金属的封接方式主要有两种：匹配封接和压缩封接。匹配封接通常选用膨胀系数比较接近的玻璃和金属（从常温到玻璃软化点的温度范围内）。封接强度主要依靠玻璃与金属表面的氧化层之间的化学键[3-4]。典型的应用是可伐材料（管壳或引脚）与硼硅玻璃的封接。

在压缩封接中，金属管壳材料的膨胀系数比玻璃膨胀系数大很多，封接冷却后在玻璃中形成挤压应力，达到封接目的。由于玻璃的抗压强度大于抗拉强度，因此这是一种理想的应力状态。例如：钢化玻璃由于表面处于压应力状态，其抗拉强度可达120 MPa以上，远高于非钢化的普通玻璃。加上玻璃与金属表面的氧化层之间的化学键作用，所以压缩封接强度比匹配封接更为牢固。例如：膨胀系数为（12~14）×10-6/℃的低碳钢与膨胀系数为9×10-6/℃的软玻璃的压缩封接[5]。

封接质量的好坏，在很大程度上取决于玻璃-金属封接界面的质量及封接界面的应力状态[6]。如果玻璃绝缘子出现缺陷甚至开裂，这些元器件的密封性、电性能和机械性能等都会因此下降。气泡、漏洞和炸裂等是玻璃-金属封接界面在生产过程中容易产生的主要缺陷。Wang[7]对Bi2O3-ZnOB2O3无铅低温玻璃焊料与预氧化的可伐合金进行了封接工艺研究，实现了500℃下的气密封装。Tandon[8]在304不锈钢外壳-铁镍合金（CTE为10.5×10-6/℃）引脚的玻璃封接中发现：虽然玻璃的CTE与引脚材料很接近，但金属外壳材料的微小塑性变形可以导致玻璃绝缘子产生很多的周向裂纹。

目前的玻璃-金属的压缩封接工艺还有待完善，封接所选取的材料和控制参数都有待进一步地探讨[9]。为此很多学者基于过盈配合进行了理论计算和有限元仿真分析。基于过盈配合、弹性变形和平面应力假设，Wu[10]针对多达5个共轴圆管的冷缩配合应力进行了计算；通过获得相邻两个圆管的配合界面的接触压力，算出界面处的周向应力和径向应力。Miraje[11]基于平面应变假设，对3层圆柱体材料的同轴压缩配合进行了理论分析。Kumaresan[12]基于平面应变假设，建立了二维仿真模型，考虑材料的塑性变形，对双圆柱体的过盈配合的极限接触压力进行了仿真分析。

文章针对一款混合集成电路模块中的金属管壳-玻璃-金属引脚之间的封接开裂失效现象，借助三维有限元仿真分析手段和理论分析手段进行了失效分析，对其中的压缩和匹配封接的手段提出了改进措施，以便降低玻璃绝缘子的应力水平。

1 玻璃-金属封接开裂的失效现象

某混合集成电路模块采用金属铝管壳封装，其不锈钢引脚通过低温玻璃熔封工艺在500℃下直接钎焊到铝管壳上，在金属引脚与管壳之间形成了玻璃绝缘子，如图1所示。模型为1/2对称，盖板未显示。

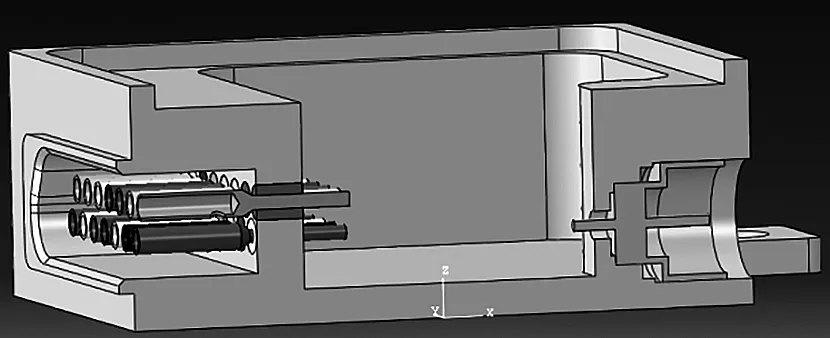
图1 管壳封装结构

在显微镜下对其进行外观检查，发现该不锈钢金属引脚四周的玻璃绝缘子存在裂纹及碎裂现象，如图2所示。裂纹大部分为径向开裂形貌，也有少部分为周向开裂。另外，玻璃绝缘子裂纹、碎裂还同时导致集成电路密封性失效。玻璃绝缘子封接处的裂纹怀疑与封装热残余应力有关。

图2 玻璃绝缘子的开裂

2 仿真模型

利用Abaqus通用仿真分析软件，建立了封装结构的力学仿真分析有限元模型，如图3所示。为了进行参数化仿真分析，同时获得高质量的有限元网格模型，从而有助于获得更加稳定可靠的仿真结果，建立了1/2对称的简化模型。该模型完全由六面体结构单元组成。图中引脚周边区域即为玻璃绝缘子。仿真模型所用的材料参数如表1所示。借助Abaqus软件的Python脚本进行二次开发，可自动地进行参数化建模仿真分析和收集结果。由于失效部位位于玻璃绝缘子，因此主要对玻璃绝缘子的应力状态与应力水平进行观察与分析。

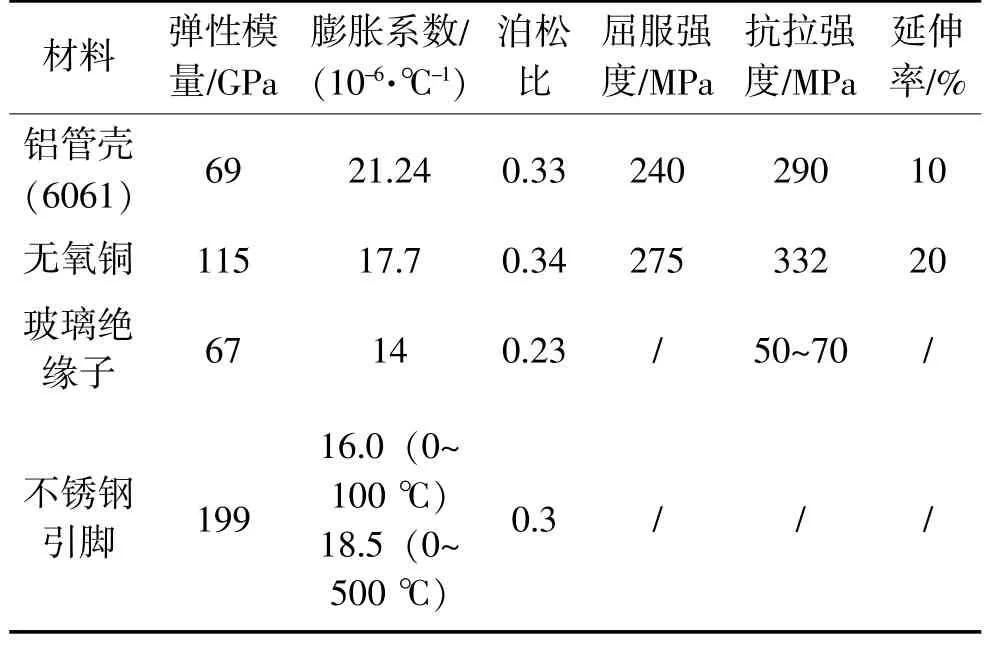
表1 仿真模型所用的材料参数

图3 封接结构仿真模型

3 仿真结果与讨论

3.1 原有的设计

采用500℃的焊接工艺将不锈钢金属引脚直接通过玻璃封接钎焊到整个铝管壳上。冷却到室温后其等效应力分布如图4所示。可以看到相邻两个玻璃绝缘子之间的金属管壳材料（铝）应力相对较大，产生了1%的等效塑性变形。由于玻璃是脆性材料，观察其最大主应力（Max Principal Stress）的分布情况。如图5所示，玻璃绝缘子内部的残余热应力达到137 MPa，大大地超过了玻璃的抗拉强度（约为50~70 MPa）[13-14]，因此，在原有的设计中，玻璃绝缘子有开裂的风险。相邻两个玻璃绝缘子的最大主应力的分布云图及其矢量分布图如图6所示。该图清晰地表明，最大主应力位于玻璃绝缘子与管壳的结合面上，而且是在玻璃绝缘子的端部。该应力本质上属于周向应力，因此在此部位，裂纹方向将主要是横向裂纹（径向裂纹）。这与实际观察到的大量开裂失效现象完全一致。

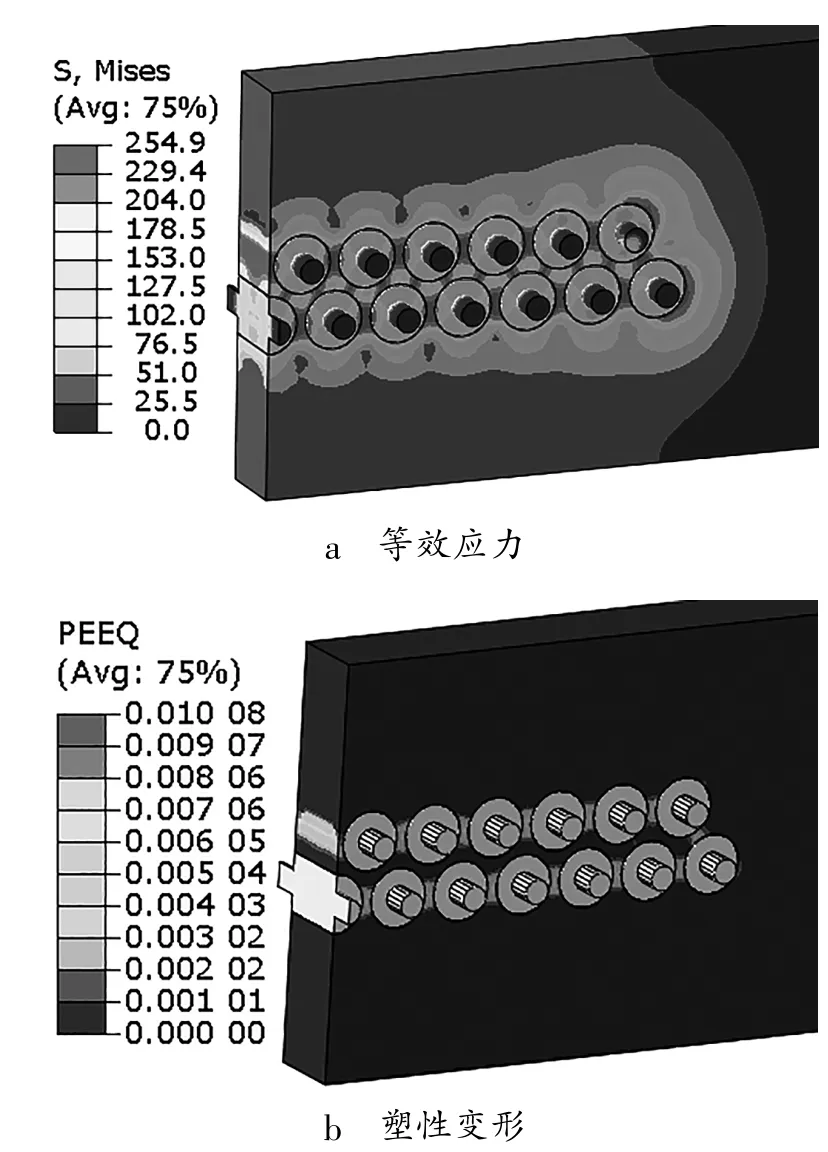
图4 等效应力与塑性变形分布图

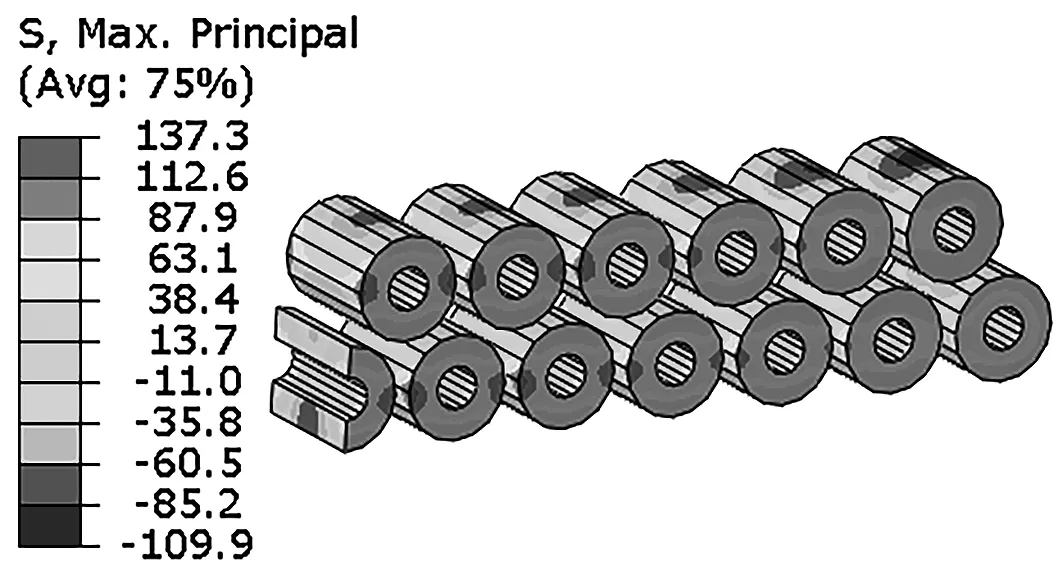
图5 玻璃绝缘子的最大主应力分布图

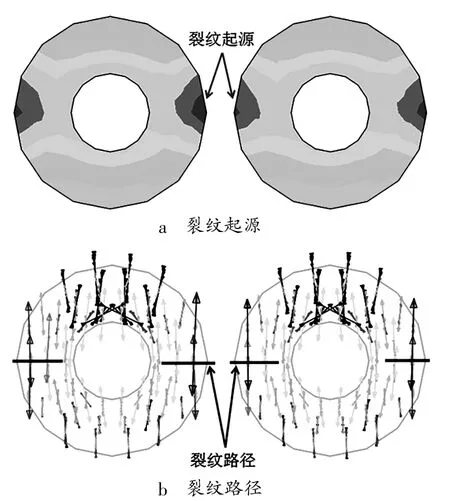
图6 玻璃绝缘子的裂纹起源与裂纹路径

原有设计的设想是，由于铝管壳的CTE（21.24×10-6/℃）比玻璃绝缘子的CTE（14×10-6/℃）大很多，从500℃工艺温度中冷却下来，玻璃绝缘子将处于压应力状态，实现压缩型紧密封接。在最大主应力分布云图中，最大主应力为正的区域处于拉伸状态，而最大主应力为负的区域处于压缩状态。为此，将图5应力云图中的压应力区与张应力区区分开来，如图7所示。可见玻璃绝缘子的绝大部分区域都处于压应力区（应力<0，用黑色来表示），与设计预想一致。不过，在玻璃绝缘子的端部，最大主应力为正，处于张应力状态。正是该局部张应力区的存在，造成了裂纹隐患。

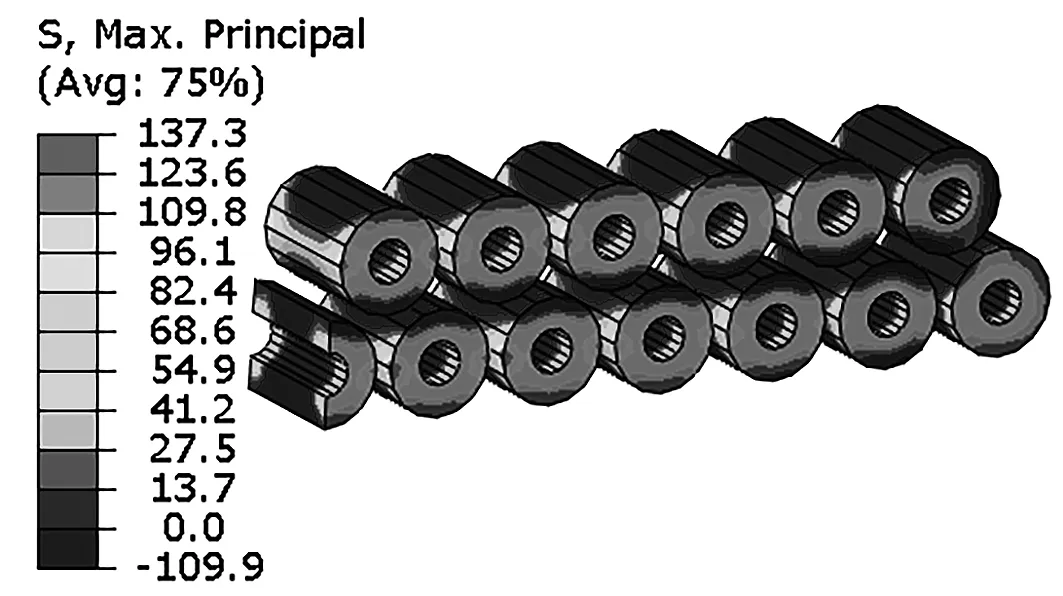
图7 玻璃绝缘子的最大主应力分布图（黑色区为压应力区）

3.2 理论分析

对单个引脚的封接进一步地建立理论分析模型，模型可以抽象为3个圆柱体进行的压缩型封接（如图8所示），其中中间的圆柱体为玻璃绝缘子，外径R=0.550 mm， 内径Ri=0.225 mm（也就是金属引脚的半径）。至于外部圆柱体的外径Ro，则与两个引脚之间的节距相关。在原有的封装设计中，引脚之间的节距为1.270 mm。不考虑熔融粘接，仅仅从热膨胀收缩紧密配合角度考虑，由于引脚的CTE=18.5×10-6/℃，大于玻璃的CTE（14×10-6/℃），因此，从高温中冷却下来，玻璃与引脚之间无法形成压缩型封接，这样，图8a的三圆柱模型可以简化为8b中的双圆柱模型。

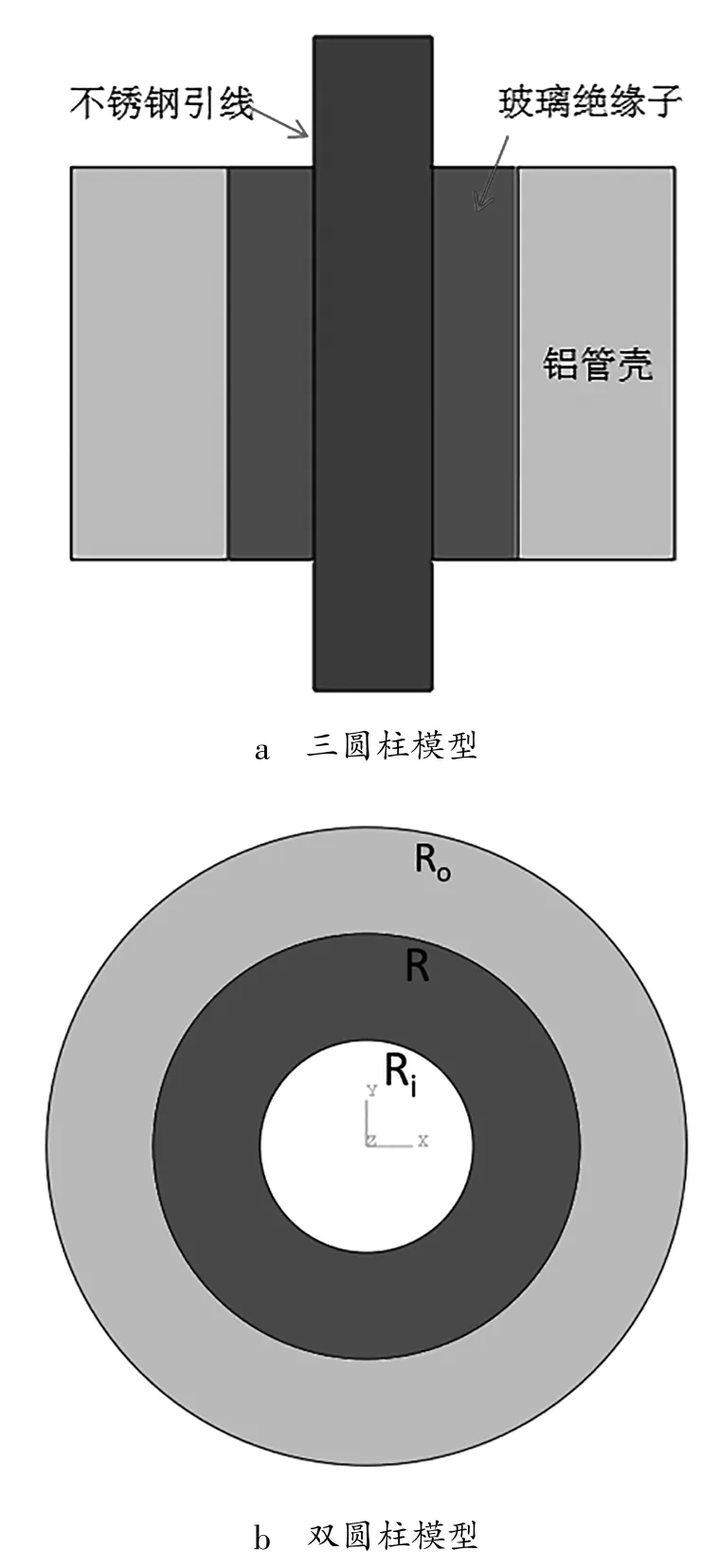
图8 理论分析模型

对于双圆柱模型，根据Lames公式[12]，在配合界面（半径为R）上，内外两个圆柱体的接触压强Pc为：

式（1）中：Eo——外部圆柱体（管壳）的弹性模量；

Ei——里面圆柱体（玻璃）的弹性模量；

υo——外部圆柱体的泊松比；

υi——里面圆柱体的泊松比；

δR——装配的过盈量。

由此得到内部圆柱体在接触面的径向应力（Radial stress）为：

内部圆柱体在接触面的周向应力（Hoop stress）为：

可见，在过盈配合的情况下，内部圆柱体的径向应力、周向应力和轴向应力均为压应力，且应力水平主要取决于接触压力（压缩封接）的大小。

根据图8的理论分析模型，有限元仿真分析得到的玻璃的最大主应力分布如图9所示（取外径Ro=0.635 mm，也就是引脚节距1.270 mm的一半）。可见，Lames公式虽然能够反映圆柱体大部分区域处于压应力状态，但不能反映材料之间轴向热膨胀收缩失配进而在绝缘子两端的张应力状态。同时，双圆柱模型得到的最大主应力对比三圆柱模型偏小，也说明不锈钢引脚对绝缘子端部的张应力是有贡献的。

图9 理论模型的有限元仿真结果

虽然如此，仍然可以根据Lames公式得出玻璃绝缘子的应力水平主要受到内外两种材料的工艺温差ΔT、膨胀系数（αO、αi）和等效管壳材料半径RO（间接地反映引脚之间的节距）的影响。

3.3 改进讨论

3.3.1分步封接方法

参考公式（8），一段长度为L，膨胀系数为α的铝杆，从高温冷却到室温，经历ΔT的温差，那么其收缩量为：

为了降低玻璃封接温度（500℃）产生的残余热应力，考虑到整个铝管壳从高温中冷却下来可能存在尺寸效应，在新的封装方案中，采用分步封接方法：先在高温500℃下将金属引脚通过玻璃封接安装到过渡性的小部件（无氧铜），然后再在低温280℃下将该过渡部件通过金锡焊料封接到铝管壳上。分步封接方案的仿真模型如图10所示。本方案降低了封装管壳的最高封装工艺温度，也就是降低了管壳工艺温度到室温的温差。小部件无氧铜则减小了500℃封接工艺下的整个部件尺寸。最终，在玻璃绝缘子中产生的热残余应力为66.66 MPa（如图11所示），比原设计的137.30 MPa降低了51.4%，效果非常明显。

图10 分步封接仿真模型

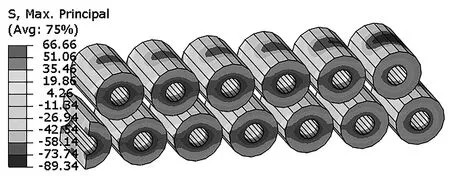
图11 分步封接工艺下玻璃的最大主应力分布

3.3.2 材料膨胀系数的匹配

在分步封接工艺的基础上，为了进一步地优化并降低玻璃绝缘子的应力水平，观察玻璃绝缘子和不锈钢引脚这两种材料的膨胀系数对玻璃应力的影响。如图12所示，当低温玻璃的CTE=12×10-6/℃，则不锈钢引脚的CTE=14×10-6/℃时，玻璃获得最优应力值为71 MPa；当低温玻璃的CTE=14×10-6/℃，则不锈钢引脚的CTE=14×10-6/℃或15×10-6/℃时，玻璃获得最优应力值为40.5 MPa；当低温玻璃的CTE=16×10-6/℃，则不锈钢引脚的CTE=16×10-6/℃时，玻璃获得最优应力值为22.5 MPa。可见，为了降低玻璃绝缘子本身的应力，绝缘子本身的膨胀系数应该大于12×10-6/℃。目前模型所用的不锈钢引脚的CTE（18.5×10-6/℃）偏大，可以通过降低不锈钢的CTE并与低温玻璃之间的CTE匹配来显著地降低玻璃的热残余应力。这属于匹配型封接的应用。

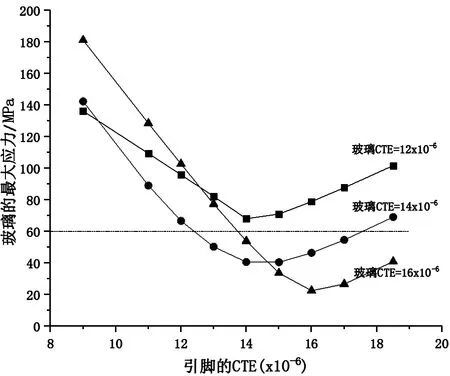
图12 不锈钢引脚CTE对玻璃应力的影响

3.3.3调整引脚间距

根据实际的工程经验，当产品中仅仅有一根引脚而不是有大量并排的引脚时，即使在500℃下将不锈钢引脚一步到位地焊接到整个铝管壳中，也极少发生玻璃绝缘子的径向开裂失效。为此，基于分步封接仿真模型及参数化建模仿真，不改变模型中材料的膨胀系数，仅仅通过调整金属引脚的数量和间距，观察对玻璃应力和与之封接的小部件的塑性变形的影响，如表2所示。其中引脚数量等于25时为分步封接模型的基准结果，其应力分布图如图11所示。

表2 引脚数量与节距的影响

由于管壳/过渡金属部件与铜之间为压缩型封接，因此，根据Lames公式，增大相邻引脚之间的距离，也就变相地增大了三圆柱理论模型中外圆柱的外径，从而加大在玻璃绝缘子中产生的压应力，有助于降低拉应力。这属于压缩型封接的应用。同时也观察到，当玻璃应力大到一定值时，与之封接的小部件也可能发生微小塑性变形。

4 结束语

在原有的设计中，玻璃绝缘子的开裂失效与其热残余应力有关。仿真结果表明，其原有的设计方案中玻璃绝缘子中的最大主应力可达137 MPa，超过了玻璃的强度极限。仿真分析表明，虽然玻璃绝缘子内部大部分区域处于压应力区，但是玻璃绝缘子的两端，仍然存在较大的局部拉应力，从而造成裂纹隐患。利用降低温差的原理，通过采用过渡小部件分步焊接的方法，降低了管壳所经历的最高工艺温度，从而可以降低整个焊接过程在玻璃绝缘子中产生的应力。利用匹配型封接原理，通过降低不锈钢引脚的膨胀系数，使之与玻璃的膨胀系数相接近，可以大大地降低玻璃的残余热应力。同时，低温玻璃的膨胀系数应大于12×10-6/℃。利用压缩型封接原理，适当地加大引脚之间的节距，也能够很明显地降低玻璃的残余热应力。通过降低玻璃绝缘子的热残余应力，提高了玻璃-金属封接的可靠性。