多中心的基于密钥策略的属性加密方案的安全性分析

何凯 庞浩霖 付有才

(1. 东莞理工学院 网络与空间安全学院，广东东莞 523808；2. 东莞理工学院 计算机科学与技术学院，广东东莞 523808)

属性基加密(ABE)[1]方案不仅可以保障数据的机密性，同时还能够实现数据的细粒度访问控制功能，被广泛的应用于云存储中。属性基加密分为基于密钥策略的属性加密[2]和基于密文策略的属性加密[3]，前者是将策略嵌入到密钥中、属性嵌入到密文中；后者是将策略嵌入到密文中、属性嵌入到密钥中。在属性基加密系统中，所有用户的私钥都是由一个中心实体生成，当实体不可信或遭受恶意攻击时，可能会造成用户密钥泄露，这样大大降低了云存储数据的安全性和保密性。为了解决该问题，多中心实体的属性基加密方案相继被提出[4-6]，这些方案支持多个不同中心实体同时操作，每个中心实体管理一组属性，并给用户拥有其属性颁发私钥。Lekwo和Waters[7]提出了一个多中心的基于密文策略的属性加密方案，其中每个中心实体无需相互协作就可以颁发私钥。Han等人[8]提出了一个多中心的基于密钥策略的属性基加密方案。然而，Ge等人[9]指出Han等人[8]方案无法抵抗共谋攻击，并提出了一种具体的攻击，即当两个拥有解密密钥的用户进行合谋时，能够为一个未授权的用户产生一个合法的私钥。随后，Y.Rahulamathavan等人[10]对Han等人的方案[8]进行了扩展，提出了一个能够抵抗用户合谋方案。然而，Zhang等人[11]发现方案[10]的解密算法存在安全漏洞，只需勾结的用户们属性集合合并起来能够满足密文访问控制策略，就能产生一个有效私钥成功地解密密文。因此，Zhang等人[11]改进了方案[10]的私钥生成算法，声称改进后方案能够抵抗共谋攻击。然而，本文在方案[11]的攻击场景的基础上，增加了一个勾结的中心实体，当未授权的用户与中心实体进行勾结，改进后的方案[11]也无法抵抗共谋攻击。

1 基础知识

1.1 准备知识

1)双线性配对。

G1和G2是素数阶p的两个乘法循环群，g是群G1的生成元，e是双线性配对，e:G1×G1→G2，双线性配对具有以下属性：

•双线性：对于所有g,h∈G1，和a,b∈Zp。有a,b∈Zp,有e(ga,hb)=e(g,h)ab。

•非退化性：e(g,h)≠1。

•可计算性：对于g,h∈G1,计算e(g,h)是容易计算的。

2)判定双线性迪菲-赫尔曼(Decisional Bilinear Diffie-Hellman，DBDH)假设。

随机选择a,b,c,z∈Zp，g是群G1的生成元，没有多项式时间算法能够以不可忽略的优势区分元组(ga,gb,gc,gabc)与元组(ga,gb,gc,gz)时，DBDH假设成立。算法的优势定义为

AdvBDBDH=|Pr[B(ga,gb,gc,gabc)=1]-

Pr[B(ga,gb,gc,gz)=1]|.

1.2 多中心的基于密钥策略的属性加密方案方案模型

1)多中心的基于密钥策略的属性加密(KP-ABE)方案由以下5个算法组成。

全局初始化：输入安全参数l，系统输出系统全局参数。

中心初始化：每个中心Ak产生自己的私钥SKk和公钥PKk和一个访问控制结构Ak。

1.3 多中心的基于密钥策略的属性加密方案的安全模型

多中心的基于密钥策略的属性加密方案安全敌手和挑战者之间的安全游戏如下：

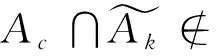
全局设置：挑战者运行Global Setup算法生成系统参数，并把它给A。

授权设置：每个授权者生成自己的私钥SKk和公钥PKk和访问控制结构Ak。

1)对于Ak∈CA, 挑战者将公、私钥对(SKk,PKk)发送给敌手A。

2)对于Ak∉CA,挑战者只将公钥发送给敌手A。

挑战：敌手A提交两个长度相同的消息m0和m1，挑战者随机选择一比特b从{0,1}中，挑战者计算挑战密文CT*=Encryption(params,mb,AC)，并将CT*发送给A。

阶段2：敌手进行密钥查询，与阶段1相同。

猜测阶段：敌手A输出b′。

2 回顾Zhang等人[11]的多中心的属性加密方案

首先，简单回顾Zhang等人的多中心的属性基加密方案[11]。

每个中心实体初始化：每个中心实体Ak选取{αk,βk,tk,1,…,tk,nk}∈RZp，并计算自己的主公钥：

和Ak的主私钥：

SKk={αk,βk,tk,1,…,tk,nk}.

中心实体Ak设定授权用户需要满足访问树结构属性的最小数量为mk(mk≤nk).

密钥生成：每个Ak选取rk,u∈RZp，并为访问树T中的每个结点x选择多项式qx。每个结点x的多项式qx的阶为dx=kx-1，其中kx是该结点的阈值。对根结点r，设定qr(0)=rk,u；对其他结点x，设定qx(0)=qparent(x)(index(x))。然后，输出用户的私钥：

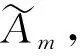
C1=m∏k∈Ice(g,g)sαk,
C2=gs,

C3=∏k∈Icgsβk,

其中Ic表示中心实体管理的属性集合的索引集。

解密：用户u首先计算D′=hu，与X,Y,Sk：

X=∏k∈Ice(C2,Dk,u) ,

Y=e(C3,D′) ,

然后，用户u计算消息m：

3 对方案[11]进行安全性分析

Zhang等人[11]提出了一个新的隐私保护多中心密钥策略的属性基加密方案，声称可以抵抗共谋攻击。然而，在其私钥Dk,u设计中，发现用户的身份u和中心实体的私钥β都在h的指数上(如huβ)。这样，所有用户的私钥之间存在线性关系，容易受到用户的共谋攻击。因此，笔者提出了一个安全性分析，表明他们的改进方案对共谋攻击是不安全的，具体分析如下。

考虑与Zhang等人的方案[11]相同的攻击场景，不同之处在于我们的攻击涉及到不怀好意的中心实体A3。假设A1,A2,A3是该系统的三个属性中心实体。

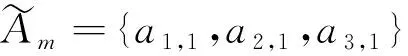
中心实体A1为用户u1生成私钥：

中心实体A2为用户u1生成私钥：

中心实体A3为用户u2生成私钥：

密文如下：

C1=m∏k∈Ice(g,g)sαk,

C2=gs,

C3=∏k∈Icgsβk,

其中Ic={1,2,3}表示中心实体集的索引。

现在，用户u1和u2利用他们的私钥，勾结中心实体A3利用他的主私钥β3，他们共谋能够计算X,Y,S如下：

X=e(C2,D1,u1)e(C2,D2,u1)e(C2,D3,u2)=

e(g,g)-s(α1+α2+α3)·e(g,h)s(u1 β1+u1 β2+u2 β3)·

Y=e(C3,hu1)·e(C2,hu1)-β3e(C2,hu2)β3=

e(gs(β1+β2+β3),hu1)·e(gs,hu1)-β3e(gs,hu2)β3=

e(gs(β1+β2),hu1)·e(gs,hu2)β3=

e(g,h)s(u1β1+u1β2+u2β3)，

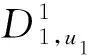
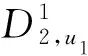
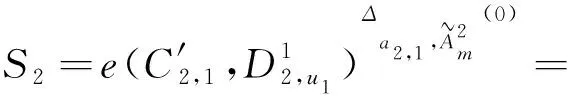
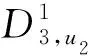
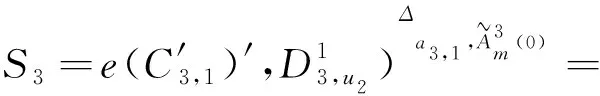
然后，用户u1与u2共谋计算

因此，

综上所述，未授权的用户u1和u2与勾结的中心实体A3一起成功地完成了共谋攻击。

此外，Han等人的方案[8]在解密算法上也有同样的问题，所以他们的方案也会遭受同样的攻击，具体攻击见附录A。

4 结语

最近，Zhang等人[11]提出一个改进的隐私保护多中心的密钥策略的属性基加密方案，声称其方案能够抵抗用户合谋攻击。然而，在安全模型下，对其方案进行了安全性分析，表明了其方案[11]不能满足抗共谋的安全要求。

附录A Han等人的多中心的属性基加密方案的安全性分析

A.1 回顾Han等人的方案

在Han等人的方案[8]中，只有密钥生成算法和解密算法与Zhang等人的方案[11]不同，全局初始化、中心实体初始化和加密是相同的。因此，仅回顾密钥生成算法和解密算法：

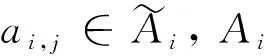
Di,u=gαihri,uh1uβi，

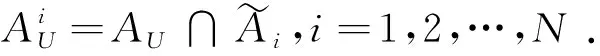
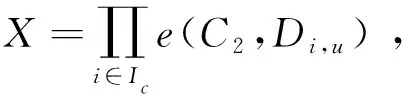
因此，

A.2 对Han等人[8]的方案进行安全性分析

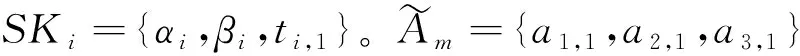
中心实体A1为用户u1生成私钥：

D1,u1=gα1hr1,u1h1u1β1,

中心实体A2为用户u1生成私钥：

D2,u1=gα2hr2,u1h1u1β2,

中心实体A3为用户u2生成私钥：

D3,u2=gα3hr3,u2h1u2β3,

密文如下：

C2=gs,

其中Ic={1,2,3}表示中心实体集的索引。

现在，用户u1和u2利用他们的私钥，而不怀好意的中心实体A3利用他的主私钥β3，他们共谋计算X,Y,S如下：

X=e(C2,D1,u1)e(C2,D2,u1)e(C2,D3,u2)=

e(g,g)s(α1+α2+α3)·e(g,h)s(r1,u1+r2,u1+r3,u2)·

e(g,h1)s(u1β1+u1β2+u2β3)，

e(g,h1)s(u1β1+u1β2+u2β3)，

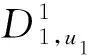
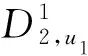
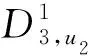
然后，用户u1与u2共谋计算

S=S1·S2·S3=e(g,h)s(r1,u1+r2,u1+r3,u2).

因此，