一种改进的多目标社区结构检测算法

杨思敏 魏文红 张宇辉

(东莞理工学院 计算机科学与技术学院，广东东莞 523808)

随着网络科学的发展，复杂网络所代表的各种复杂系统已广泛应用于许多领域，例如生物网络、社交网络以及交通网络等[1-3]。复杂网络具有许多重要特性，社区结构就是其重要特性之一[4]。一般而言，社区结构具有内部节点间连接紧密而社区间连接稀疏的特征[1]。社区检测依照社区结构特性，将整个复杂网络划分成几组节点(即社区、模块或者集群)[5]，这有利于发现复杂网络潜在规律，解决生活实际问题。例如，要解决交通堵塞问题，需要了解交通网络布局概况，获取容易拥堵的关键区域；要阻断网络流言传播，需要哪些群体更具有流言传播快的特点；要防止疫情蔓延，就要了解哪些人群更容易被感染等等。

为更好地研究复杂网络，科研人员相继提出了许多社区检测算法。Girvan和Newman提出基于最大边介数算法(GN)[6]，该算法依次删除网络中具有最大边介数的边，以达到社区划分的目的，而该算法每次搜索都需要花费大量的时间。为解决GN算法的时间消耗问题，Blondel等提出了一种基于层次聚类的快速模块度优化算法(BGLL)[7]，该算法分成两个阶段不断优化模块度Q[8]，以最快时间达到最好分区效果，但该算法存在容易陷入局部最优的现象。Pizzuti等利用具有超强随机性的遗传算法，以增加解的多样性找到全局最优解，提出了基于遗传算法的社区检测算法(GA-Net)[9]。前面所述算法皆为单目标优化算法，并不能同时优化多个目标条件。随着多目标算法应用越来越广泛，Pizzuti根据社区结构的特征，将社区检测问题建模成多目标优化问题，并提出了MOGA-NET算法[10]。虽然MOGA-NET可以得到一个较好的社区划分，但由于采用邻接轨迹的编码方式，使存在种群多样性不足，社区划分准确度不够高的缺陷，特别是针对小型的网络，所以笔者提出ICDMOGA-NET算法应用于社区检测。

ICDMOGA-NET在编码阶段采用向量编码方式，打破了基于邻接轨迹编码方式的约束，增加编码多样性从而增加种群多样性。在进化过程中，利用双向交叉算子增加个体间信息的交流，并将统一变异方式作为变异策略，以增加节点与所属社区间的粘合度，达到更好的社区划分效果。经过改进，该算法在空手道俱乐部真实网络上的模块度Q以及归一互信息NMI分别提高约3.01%、12.63%，对海豚社交网络的平均模块度Q提高约11.3%。

1 问题描述

通常社区被定义为社区内部节点之间连接紧密，社区之间连接稀疏的一组节点[1]。而在更标准的定义中，社区又可以分为强社区和弱社区，一个强社区一定是弱社区[11]。本文主要对弱社区的检测。

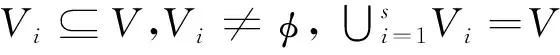
选取Kernel K-means(KKM)[13]和Ratio Cut(RC)[14]为两个目标函数f1,f2，并最小化这两个目标函数。f1表示社区内部的连接密度，f2反映社区外部的连接情况。这两个目标的目标函数如下：

(1)

(2)

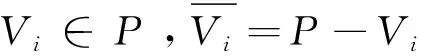
2 算法描述

2.1 个体表示

在社区检测中，通常采用基于邻接轨迹的编码方式[12]，而ICDMOGA-NET则采用向量编码方式[2]。首先，将整个网络编码成一个整数串：X={x1,x2,…,xn}，其中n是网络节点的总数。xi表示第i个节点的社区标识符(即基因)，在[1,n]范围内随机产生。ICDMOGA-NET算法将具有相同社区标识符的节点划分在同一个社区内，所以一个个体至多可以分解成n个社区。如图1(a)表示由9个节点组成的网络N，图1(b)图G是由网络N抽象出来的图，经向量编码后产生形成个体图1(c)，再经过解码后分解成两个社区图1(d)。

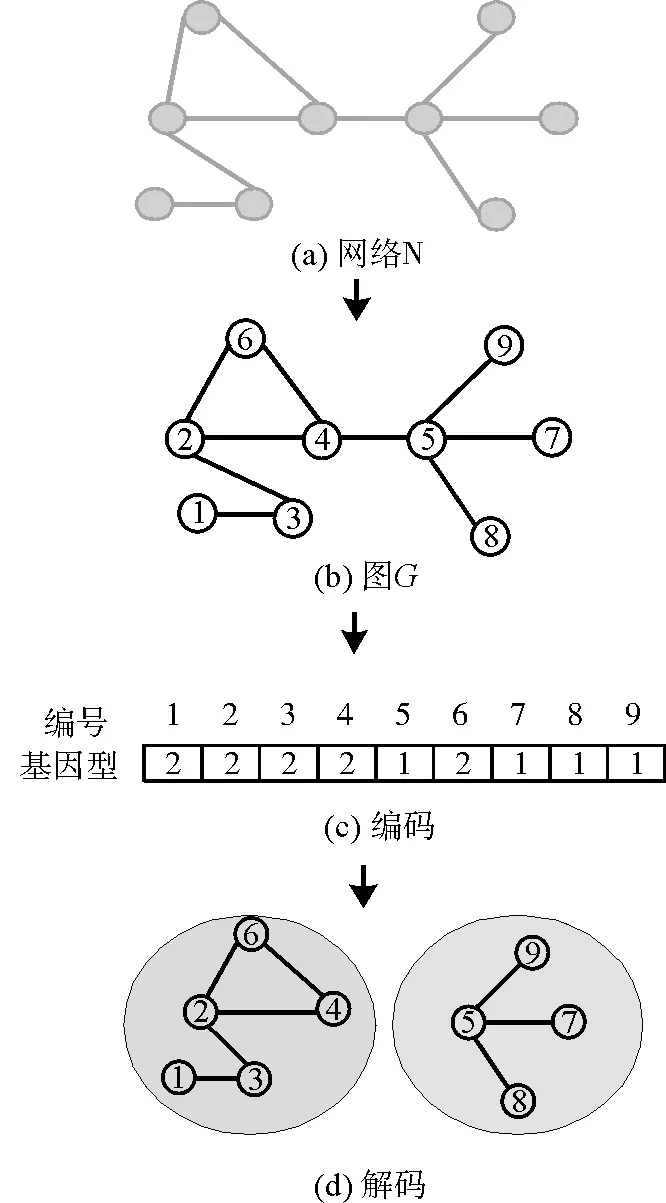
图1 网络编码解码

2.2 交叉算子

一般来说，染色体重组通常采用单点交叉方式，即随机选择两个个体作为父代，并任意选择一个位置编号作为开始交叉的起点，从起点开始进行个体间的基因交换，从而产生子代。在本文提出算法中，采用双向交叉的方式[15]从种群中任意选取两个个体a、b，并随机选择第i个位置。先以个体a为模板，获取个体a第i个位置所对应的社区标识符label1，找到个体a中所有社区标识符为label11的位置，将个体b在相应位置上的标识符替换成label1，从而产生新个体b1，然后以b为模板重复上述步骤，产生新个体a1，这样就完成一次双向交叉操作。如图2，从a中随机选择第4个位置，a的第4个位置的标识符为1，然后找到a中所有标识符为1的位置编号，分别为2、4、6，再将b中位置编号为第2、4、6的标识符全部更改为1，此时得到新个体b1；b的第4个位置编号对应的基因为3，在b中找到标识符为3的所有位置编号，分别为4、7，将a的第4、7位基因编号上的标识符替换为3，得到新个体a1。

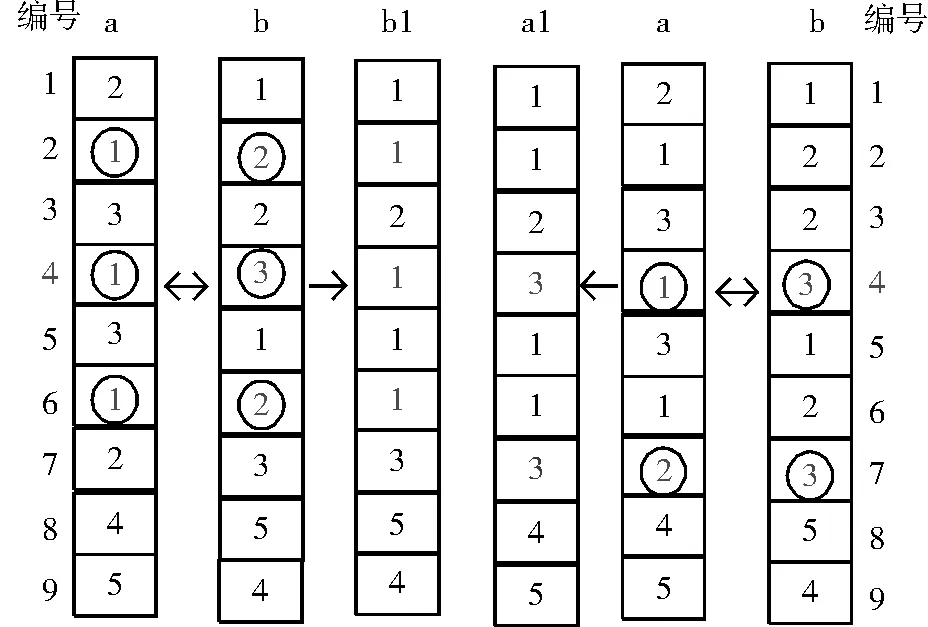
图2 双向交叉示意图

2.3 变异算子

不同的社区检测算法，因为编码方式的不同，会有不同的变异策略。由于本文采用向量编码方式，所以使用统一变异算子策略，以增加种群多样性。先从种群中随机选择需要突变的个体，并从突变个体中随机选择需要突变的第i个社区标识符，将所有与第i个节点相邻的其他节点所对应的社区标识符替换为节点i的社区标识符。对图1中的图G变异过程如图3所示，先从种群中随机选择变异个体如图3(a)；再从个体中随机选择第8个基因编号作为变异点如图3(b)，其对应的标识符为2；由图1中的网络N可知，第8个节点的邻接节点是第5个节点，所以将第5个节点的社区标志符替换为2，如图3(c)所示。

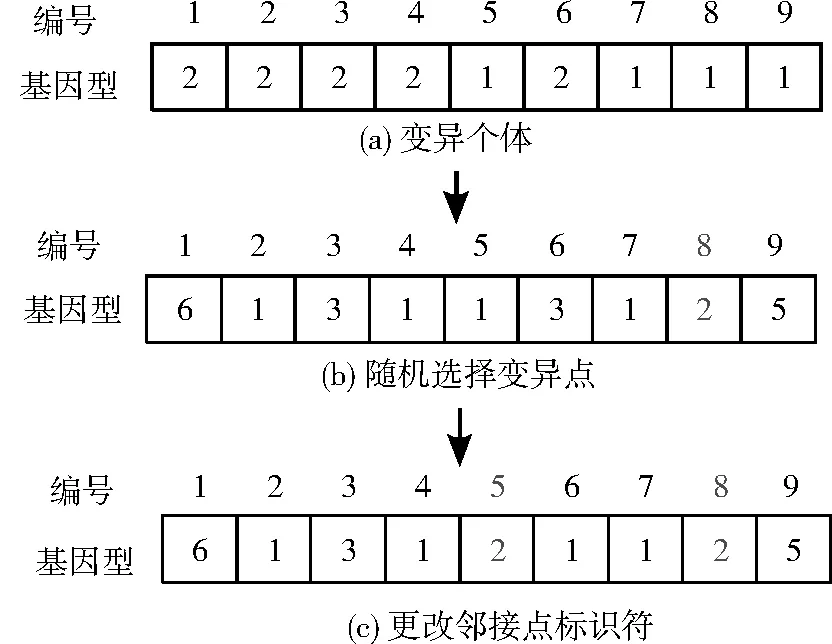
图3 变异过程

2.4 算法步骤

将网络N抽象成图G=(V,E)，其中V表示节点集合，E表示边集合。随机初始化种群，为每个个体随机匹配社区标识符。每个个体可以解码生成多个图结构，且每个图均为图G的子图。利用多目标算法对每个个体进行评估，并根据Pareto优势为每个个体分配等级并进行排序，再利用改进后的交叉算子以及变异算子增加种群多样性，产生新的种群。ICDMOGA-NET具体算法构造如算法1，图4为ICDMOGA-NET算法流程。

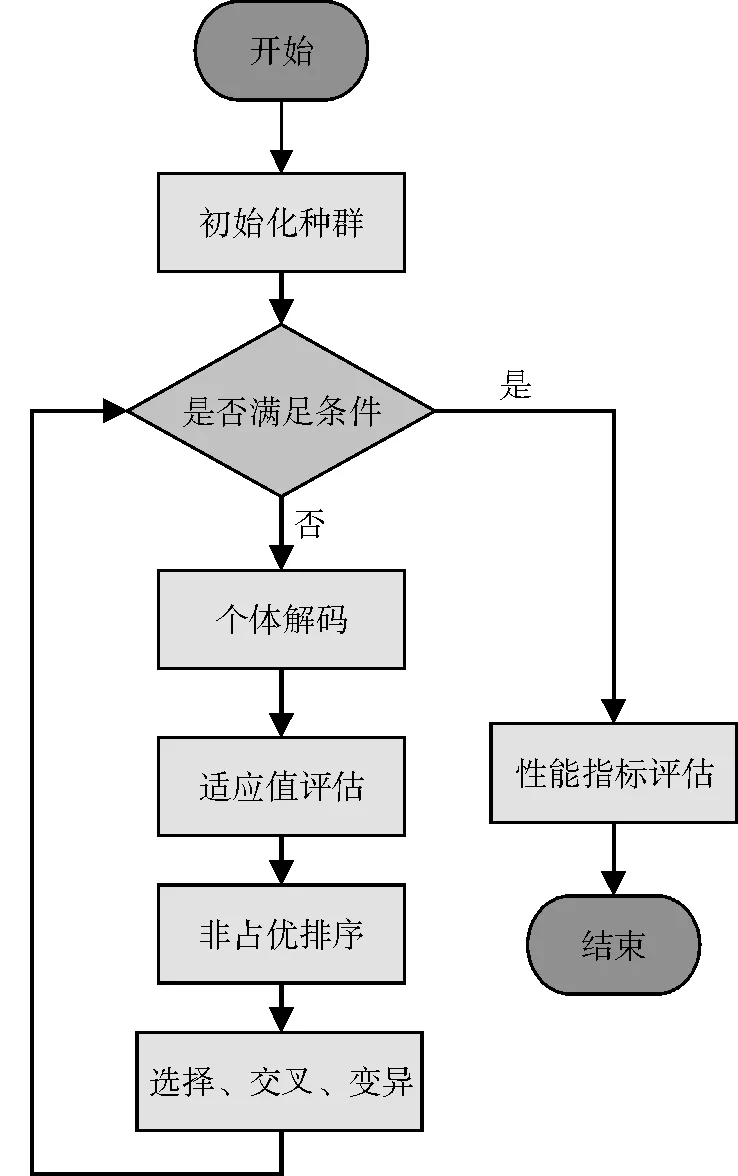
图4 ICDMOGA-NET算法流程

算法1 ICDMOGA-NET算法

Input:网络N，并建模成图为G=(V,E)

Input:目标函数f1,f2，迭代次数t，规模POPOSIZE

1)随机初始化种群，个体长度为|V|

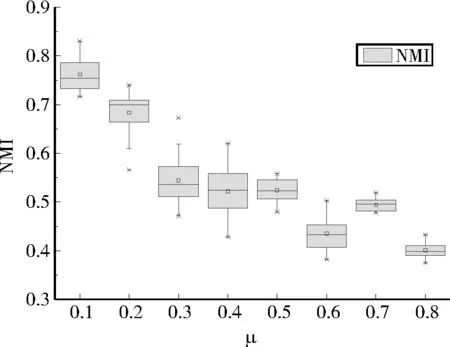
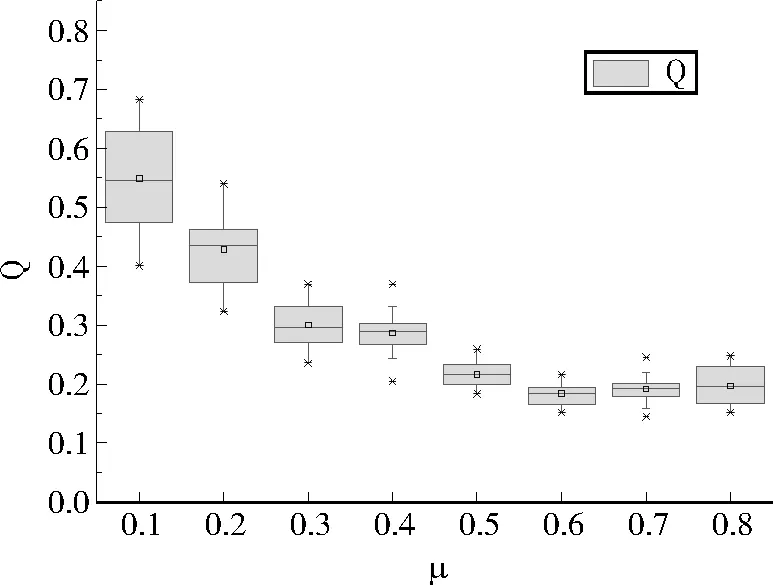
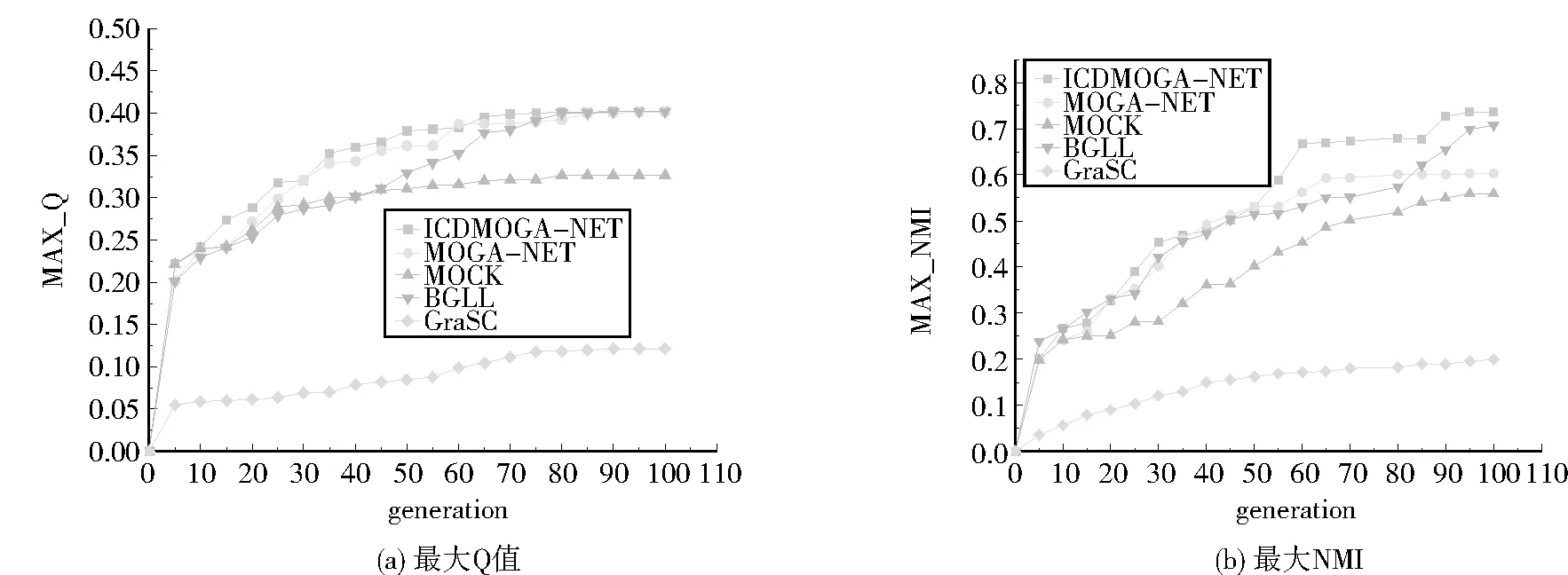
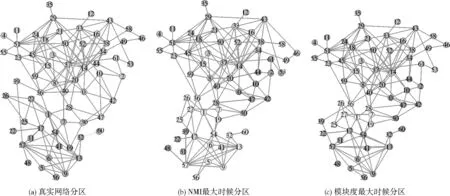
2)Whilei

3) 解码，分解个体。

4) 利用目标函数评估个体

5) 非占优排序

6) 选择个体

7) 交叉产生新个体

8) 变异产生新个体

9)选择性能指标最好个体

10)return 最佳社区划分

3 实验分析

3.1 性能指标

模块度Q能够评估网络的社区划分结果的好坏。它是一种内部度量，可用于评估社区结构偏离随机性的程度[12]。其定义如下：

(3)

m是整个网络的边数，Aij表示在邻接矩阵中节点i与节点j是否存在边，如果是，则Aij=1如果不是，则Aij=0。ki与kj分别表示节点i与节点j的度。d(Vi,Vj)用来判断节点i与节点j是否在同一个社区内，如果是，则d(Vi,Vj)=1，如果不是，则d(Vi,Vj)=0。

归一化互信息(NMI)用以评估网络真实划分与网络算法划分之间的相似度[16]。如果两个分区内部社团划分越接近，则NMI得值越接近1。当NMI的值等于1时，则算法划分完全与真实网络划分一致。NMI定义如下：

(4)

T表示网络的真实划分情况，P表示利用算法划分的网络情况，则MT为网络真实划的社区个数，MP为网络算法划分的社区个数。矩阵M是一个混淆矩阵，Mij表示节点既在分区T第i个社区又在分区P第j个社区的个数。Mi表示混淆矩阵M第i行的和，Mj表示混淆矩阵M第j列的和。

3.2 环境配置与实验配置

实验环境配置：

操作系统：win10；内存：8G；处理器：Intel(R) Core(TM) i5-8250U；主频：1.60GHz。

实验配置：

独立运行次数：20次；迭代次数：100代；种群规模：200。

3.3 合成网络实验

Lancichinetti[17]在2008年提出一种基准测试网络(LFR)，该网络节点度数和社区大小均服从指数分布。每个节点与其社区节点的连接比率为μ，而与其他社区顶点连接的比率为1-μ。μ是混合参数。通过控制μ可以控制社区的大小。本文将μ从0增加到0.8，每次增加0.1，生成8个合成网络。图5和图6表示8个合成网络通过ICDMOGA-NET独立运行20次后，所得到的最大NMI和Q的值。实验结果表明随着μ的不断增大，即合成网络的复杂度增大，NMI和模块度Q的值在不断减小，并逐渐维持一个相对稳定位置。

图5 合成网络NMI对比

图6 合成网络模块度Q对比

3.4 真实网络实验

本实验主要对空手道俱乐部关系网络(Zachary’s Karate Club Network)[18]以及海豚社交网络(Dolphin Social Network)[19]两个真实网络进行测试。空手道俱乐部关系网络是对一个美国大学空手道俱乐部进行观察而构建的真实的社会网络。网络包含34个节点和78条边，其中节点表示俱乐部成员，边表示成员之间存在关系。经过观察，该网络在现实社会中被划分为2个社区。实验是对无权重的空手道俱乐部关系网络进行测试。海豚社交关系网络是通过观察生活在新西兰Doubtful Sound海峡的62只海豚群体的交流情况而形成。该网络具有62个节点，159条边，节点表示海豚，而边是指频繁接触的海豚。该图为无权图。

实验独立运行20次，每次迭代100代，种群规模为200。为比较算法性能，本文选择MOGA-NET[10]、基于k值的多目标聚类算法(MOCK)[20]、BGLL[7]以及多目标集群算法(GraSC)[21]进行比较。通过ICDMOGA-NET得到Pareto前沿如图7所示。通过实验,由表1可知，与MOGA-NET、MOCK、BGLL、GraSC相比，ICDMOGA-NET对空手道俱乐部关系网络的社区检测可以获得更大的NMI和Q其社区划分效果更好，对海豚社交关系网络进行社区检测的时模块度Q的值维持在0.4以上，说明ICDMOGA-NET具有一定的稳定性。图8、图9分别表示ICDMOGA-NET对空手道俱乐部关系网和海豚社交网络一次运行时Q和NIM的变化，每隔5代记录一次，由结果可知，在一次运行中，ICDMOGA-NET可以加快收敛，更快接近最优值。图10、图11为通过ICDMOGA-NET算法网络划分与真实网络划分对比，得到本文提出算法在空手道俱乐部关系网上有较好的社区划分，而对海豚社交网络所得到的社区个数大于真实社区划分的个数,可以细化社区划分。

表1 ICMDGA-NET与其他算法对比结果

图7 两个真实网络的Pareto前沿

图8 ICDMOGA-NET与其他算法在空手道俱乐部关系网运行一次的过程

图9 ICDMOGA-NET与其他算法在海豚关系网一次运行的过程

图10 由ICDMOGA-NET检测到空手道俱乐部关系网分区

图11 由ICDMOGA-NET检测到海豚社交关系网分区

总体而言，ICDMOGA-NET相较于MOGA-NET在空手道俱乐部关系网络上Q以及NMI分别提高约3.01%、12.63%，在海豚社交网络上的平均模块度Q提高约11.3%，并且与MOCK、BGLL以及GraSC相比，ICDMOGA-NET具有较大的优越性。因为ICDMOGA-NET结合向量编码方式，该编码方式有比较强的随机性，以至提高种群的多样性，增大搜索最优社区的可能性，且双向交叉策略加强节点之间的信息交流，因此ICDMOGA-NET针对小型网络可以有更好的效果。

3 结语

本文提出一种基于MOGA-NET改进的多目标社区结构检测算法。该算法采用向量编码方式、双向交叉算子以及统一变异算子，以增大种群的多样性，提高个体间信息交流。通过合成网络实验可知，本文算法所得的结果随着μ的增大而减小。说明网络的复杂程度越大，ICDMOGA-NET的社区划分难度也在增大。在真实网络实验中,与MOGA-NET、MOCK、BGLL、GraSC相比，针对更小型的网络ICDMOGA-NET具有更高的精确度。在今后研究中，可以从降低时间开销、增加节点之间关联性的搜索机制等，对ICDMOGA-NET进行拓展。