弹性波模拟中局部透射边界的反射特征及参数优化

邢浩洁， 李小军， 刘爱文， 李鸿晶， 周正华， 陈 苏

(1. 中国地震局 地球物理研究所，北京 100081； 2. 北京工业大学 建筑工程学院，北京 100124；3. 南京工业大学 土木工程学院，南京 211816； 4. 南京工业大学 交通运输工程学院，南京 211816)

地球物理、地震工程、计算声学等领域的无限介质波动问题常常使用有限计算模型来模拟，此时需要设置适当的人工边界条件来消除人为截取边界所造成的虚假反射，以确保模拟结果的合理性[1-2]。提高复杂波动问题模拟中的边界精度是地球物理正、反演模拟，强地震动场地效应分析，土与结构动力相互作用计算等重要技术的基础共性需求。不同于力学领域传统的Dirichlet边界(固定边界)和Neumann边界(自由边界)会将射向边界的外行波完全反射回计算区域，人工边界条件采用时空外推、应力平衡或区域衰减等方式，使计算得到的边界节点运动与原来实际问题中该处运动基本一致，从而实现外行波在人工边界上的无反射(或表述为透射、吸收、辐射、单向波动等)。

多次透射公式(multi-transmitting formula, MTF)[3-4]是一种重要的人工边界条件，它基于直接模拟任意外行波的一般传播过程而建立，具有形式简单、精度可控、易于与各种内域离散格式相结合等优点。MTF已广泛用于海洋地震工程所关心的两相介质波动问题[5-7]、局部地形对弹性波的散射问题[8]、大坝-地基系统地震反应分析[9-10]、核电结构-场地土系统地震反应分析[11-12]等数值模拟当中。近几年，MTF被用于高精度谱元法的地震波动模拟[13-16]，能够与这种不等距节点的离散格式很好地结合，显示出该边界具有极强的适应能力。除了上述应用之外，透射边界的稳定实现是一直以来该边界研究的重点，研究结果主要包括：边界失稳是随着波在计算模型内部和边界之间来回反射逐步积累的；一种小量修正的MTF公式能够消除漂移失稳，在整个计算模型中注入小阻尼能够消除振荡失稳[17]；GKS(Gustafsson-Kreiss-Sundström)定理的群速度解释表明在集中质量有限元格式中MTF会出现振荡失稳，而在二阶中心差分格式中则不会[18]；在边界附近添加弹簧和阻尼力学元件能够抑制MTF的漂移失稳[19]；在一种修正的集中质量有限元格式中MTF能够给出长持时稳定的模拟结果[20]；在波导问题模拟中可以通过控制单元长宽比来避免MTF出现振荡失稳[21]。

为了提高透射边界模拟复杂波动问题的精度，文献[22]提出一种在多个不同方向上分别使用MTF再将结果加权平均的多向透射边界；文献[23]基于无穷大波速假定提出一种推广的透射边界，它在原MTF基础上增加了对接近掠入射的外行波的模拟能力。最近，Xing等[24-25]基于已有研究揭示的MTF与Higdon边界之间的密切联系，将后者所具有的多种计算波速配置引入前者，提出一种基于多人工波速的新型局部透射边界。然而，目前关于透射边界精度严格的理论分析(这里指反射系数)主要基于单分量波动给出，而地震波作为一种弹性波，是典型的多分量波动。Shi等导出了现有MTF边界对饱和多孔介质弹性波的反射系数，其中二阶MTF对一些波动成分的反射比例能达到0.25～0.35左右，这大大高于单分量波动的反射系数所给出的结果。因此，需要专门研究多分量波动情形下透射边界的反射特征并进行参数优化。本文将针对新提出的多人工波速局部透射边界，导出其弹性波反射系数的严格表达式，据此详细探讨影响边界反射特征的各方面因素，最后给出复杂波动情形的边界参数取值建议。

1 一种新型局部透射边界

1.1 多次透射公式

在图1所示的局部复杂场地模型中，围绕各个人工边界节点统一定义一种局部坐标s0t，其空间轴s位于从边界节点0指向内域的任意离散网格线上，正方向向内，时间轴t与整体模型一致。那么，用于推算任意时刻各个人工边界节点运动的多次透射公式(MTF)[1]为

(1)

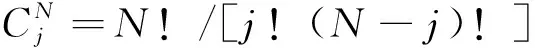
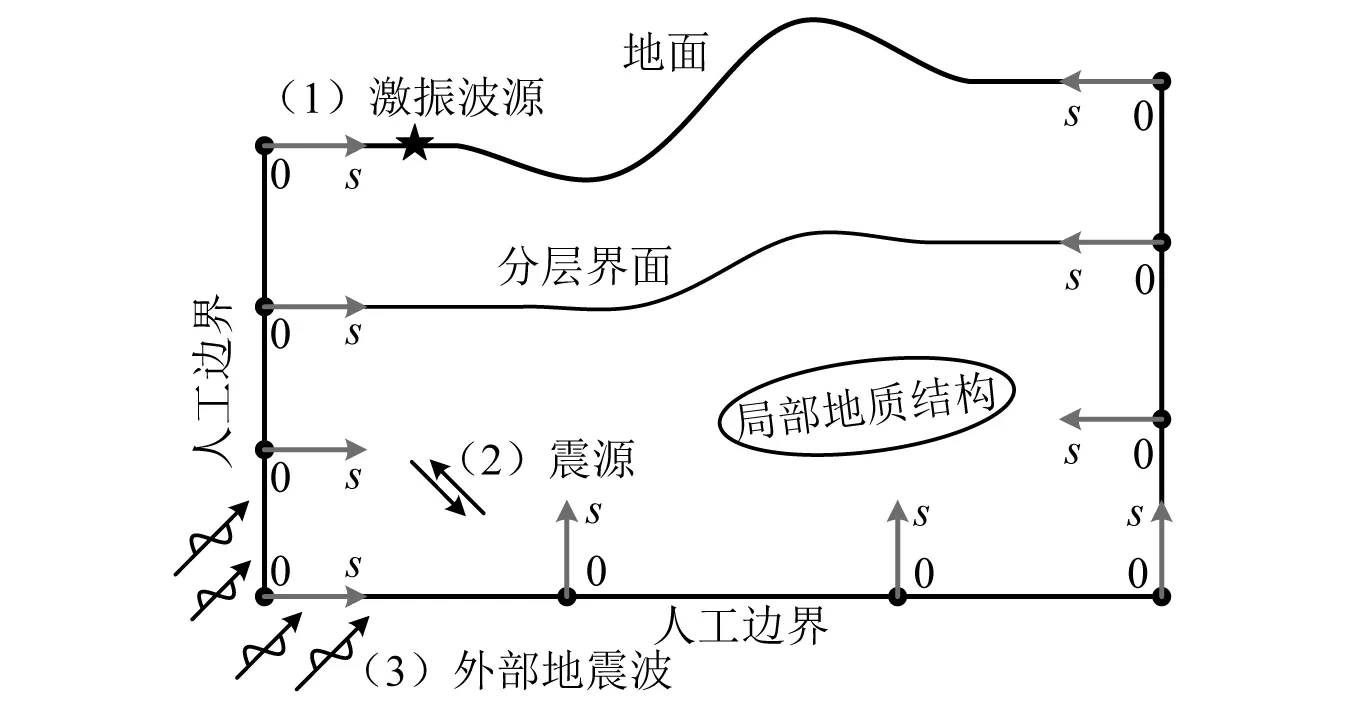
图1 用于定义透射边界的统一局部坐标s0tFig.1 The unified local coordinates s0t that are used to define transmitting boundaries

如果用B(ca)表示时空移动算子，其含义为

B(ca)u(s,t) ≡B(caΔt, -Δt)u(s,t) =u(s+caΔt,t-Δt)

B2(ca)u(s,t) =B(ca)[B(ca)u(s,t)] =u(s+2caΔt,t-2Δt)

依次类推，则MTF可以简洁地表示为如下离散算子形式

[I-B(ca)]Nu(s,t)=0

(2)

图2绘出了二阶和三阶MTF的离散参考点在局部坐标s0t中所处的位置。可以看出，这些参考点依次由离散算子B(ca)及其乘方B2(ca),B3(ca), …所确定。由于这里只有一种人工波速ca, 故所有参考点等距离分布于一条倾斜直线(图2中虚线)上。MTF即为根据这些离散参考点的运动外推人工边节点运动的表达式。

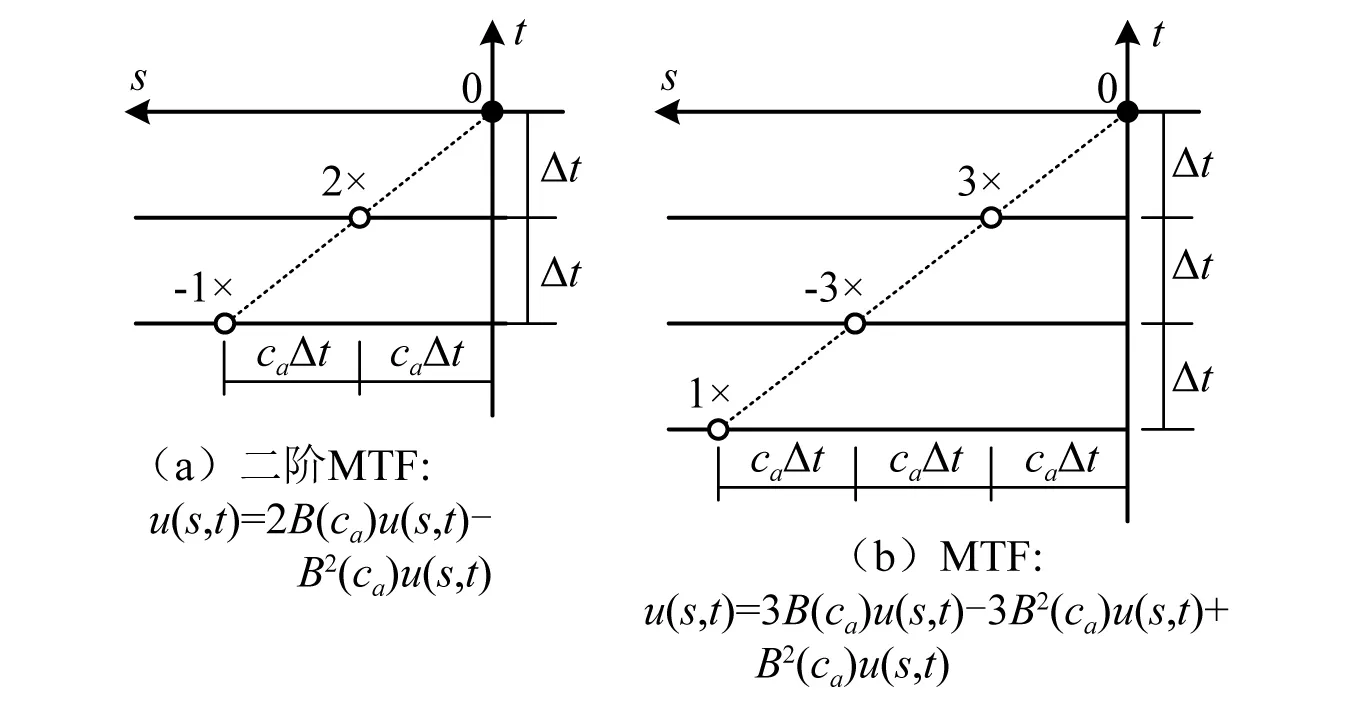
图2 二阶和三阶MTF边界的离散参考点Fig.2 Discrete reference points of the 2nd-and 3rd-order MTF boundaries

1.2 一种新型局部透射边界

将边界表达式(2)中的N个相同的离散算子I-B(ca)替换为基于多个人工波速caj(j= 1, …,N)的N个不同的离散算子I-B(caj)。利用上述时空移动算子B(ca)的含义及乘积规则，此时有

B(ca1)u(s,t)≡B(ca1Δt,-Δt)u(s,t)=u(s+ca1Δt,t-Δt),

B(ca1)B(ca2)u(s,t) =u(s+ca1Δt+ca2Δt,t-2Δt),

B(ca1)B(ca2)B(ca3)u(s,t)=u(s+ca1Δt+ca2Δt+ca3Δt,t-3Δt)

依次类推。于是，导出一种基于多个人工波速的新型局部透射边界，其表达式为

(3)

为了直观地体现新边界与传统单一人工波速MTF的联系和区别，将边界式(3)简记为caj-MTF。

图3绘出了二阶和三阶caj-MTF的离散参考点在局部坐标s0t中所处的位置。由此可以看出，新边界对MTF的优化是通过将原来单个参考点运动2倍、3倍分别替换为2个、3个不同参考点运动之和来实现的。如果从MTF“误差波多次透射”的物理机制角度来分析caj-MTF，那么后者可以看作是保留了“多次透射”过程，但优化了对各阶“误差波”的描述。

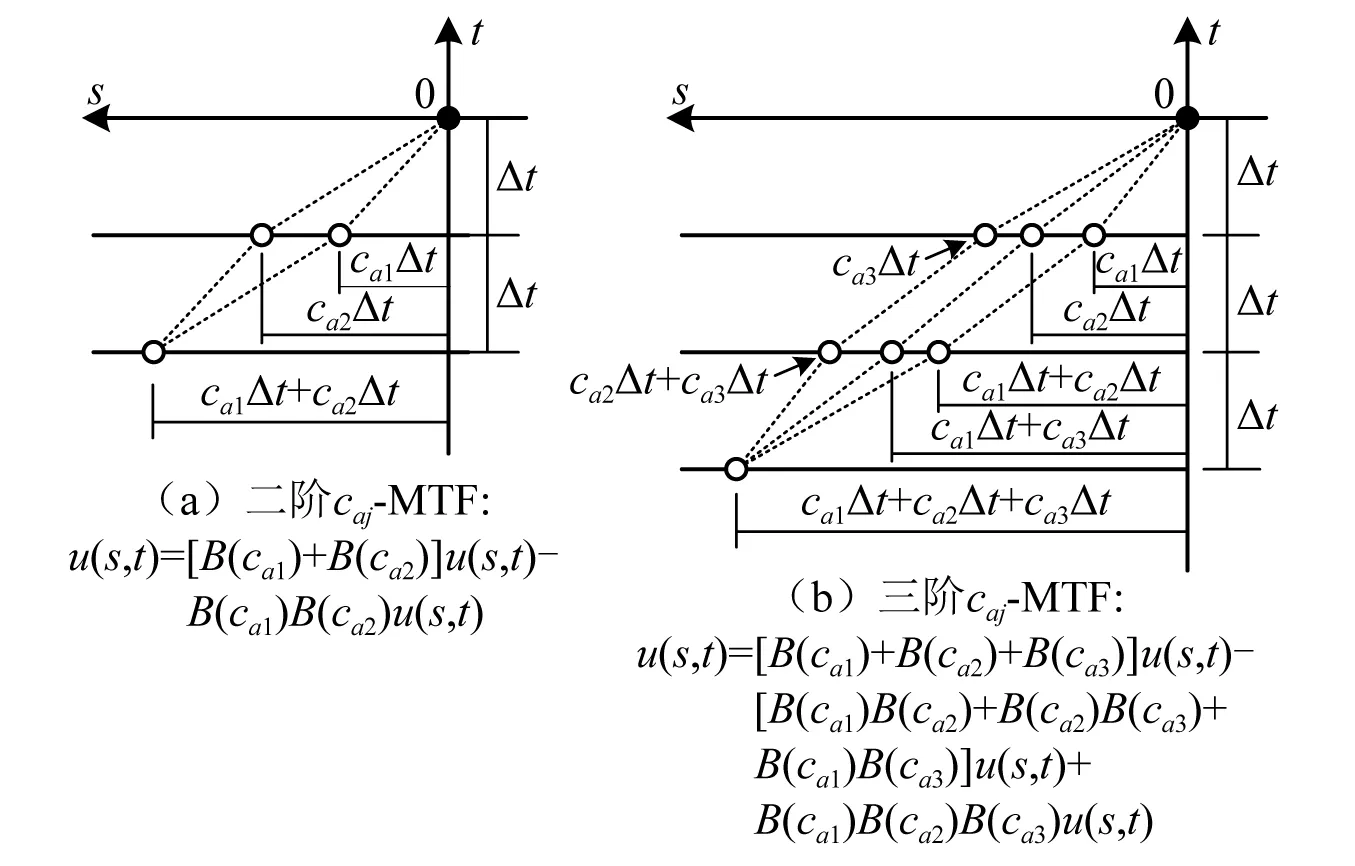
图3 二阶和三阶caj-MTF边界的离散参考点Fig.3 Discrete reference points of the 2nd-and 3rd-order caj-MTF boundaries

1.3 数值计算格式

caj-MTF的数值计算格式可分为两种情形：对于离散节点在人工边界附近为等距离分布情形(如有限元或各种有限差分模型)，可以借鉴景立平研究的算子替换法。对于离散节点在人工边界附近为非等距分布情形(如谱元离散模型)，则可以采用廖振鹏研究的6.1.1节的简单内插方法。第一种情形最为常见，这里给出其数值计算格式的具体表达式，第二种情形将另文探讨。

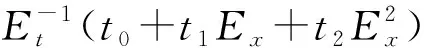
(4)

其中

sa1=ca1Δt/Δs,sa2=ca2Δt/Δs,sa3=ca3Δt/Δs

(5)

qx0=(sa1-1)(sa1-2)/2,qx1=-sa1(sa1-2),

qx2=sa1(sa1-1)/2

(6)

rx0=(sa2-1)(sa2-2)/2,rx1=-sa2(sa2-2),

rx2=sa2(sa2-1)/2

(7)

sx0=(sa3-1)(sa3-2)/2,sx1=-sa3(sa3-2),

sx2=sa3(sa3-1)/2

(8)

将式(4)中3个乘积项分别只保留一项、两项，即为一阶、二阶caj-MTF的数值计算格式。

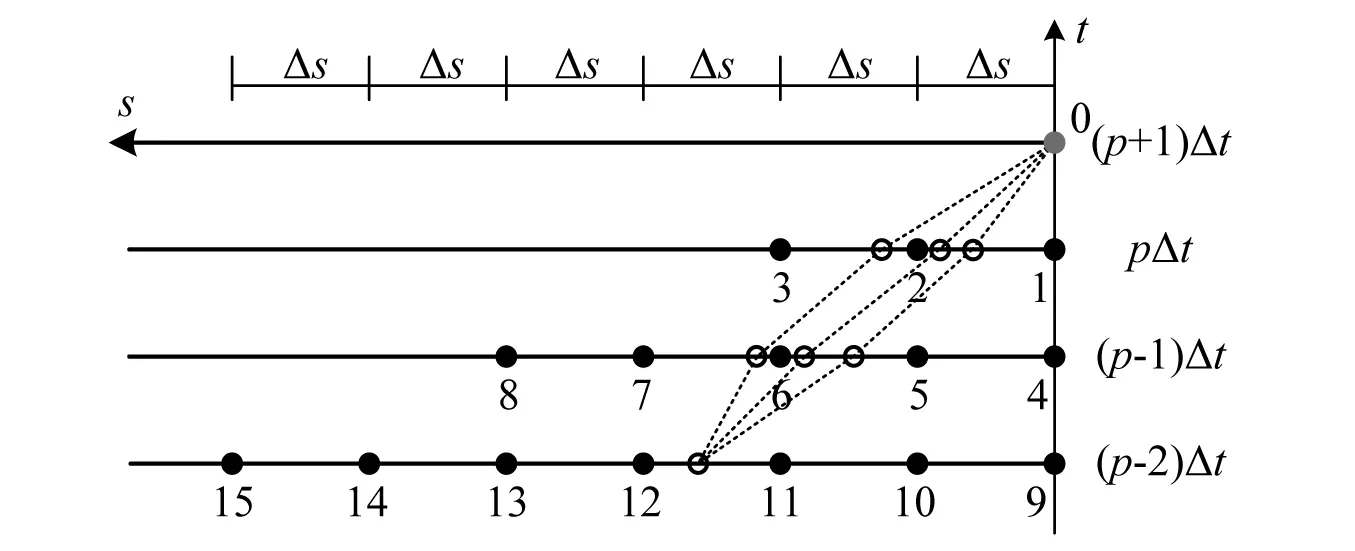
图4 caj-MTF数值计算格式中离散节点的统一局部编号Fig.4 Unified local numbering of the discrete nodes involved in the numerical schemes of caj-MTF

逐步展开式(4)，并利用图4中离散节点的统一局部编号，导出一阶、二阶、三阶caj-MTF数值计算格式的最终形式如下

(9)

(10)

(11)

(T1)1×3=Qv

(12)

(T2)1×8=[T2_1-T2_2]

(13)

(15)

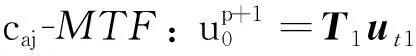
(16)

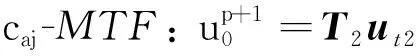
(17)

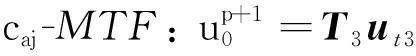
(18)

式中：带下标的粗体变量表示由计算系数组成的行向量或由节点波场值组成的列向量；上标T表示转置；括号下标( )1×3, ()1×8, ()15×1等仅是为了便于理解，用来标示出各个向量的维度，在实际编程时应忽略。式(15)中涉及的统一局部节点编号见图4。

式(5)～式(18)组成了前3阶caj-MTF实用的数值计算格式。可以看出，它与廖振鹏的研究中现有MTF的数值计算格式一样简洁。

2 弹性波反射系数

这一章将导出所提出的新型局部透射边界对弹性波的反射系数，作为后文进行边界反射特征与参数优化分析的依据。

现有MTF的反射系数基于等距离散参考点上的振动解导出，但本文caj-MTF的离散参考点为不等距分布，难以沿用这个方法。不过，根据现有研究所揭示的离散形式MTF边界与经典的连续形式Clayton-Engquist以及Higdon边界之间的密切联系，可以导出与caj-MTF等价的连续边界形式，在后者基础上导出所需的弹性波反射系数。刑浩洁等的研究证明了边界式(3)中各个离散算子(I-B(caj))等价于连续形式的一维波动微分算子(∂/∂t-caj∂/∂s)，因此与边界(3)等价的连续边界形式为

(19)

式(19)仍然定义在图1所示的统一局部坐标当中，空间轴s可以表示整体模型的x，y，z轴或者任意一条倾斜的离散网格线。

从文献[26-28]得知，求解边界反射系数的步骤为：先写出入射波的谐波表达式；再将入射波与反射波(等于入射波乘以反射系数)组成的波场代入边界条件；约去不必要的部分，即可得到反射系数。平直界面对弹性波的反射有P波入射和S波入射两组模式，前者存在P-P，P-S反射系数Rpp，Rps，后者有S-P，S-S反射系数Rsp，Rss。不失一般性，考虑图5所示的坐标系与外行波情形。

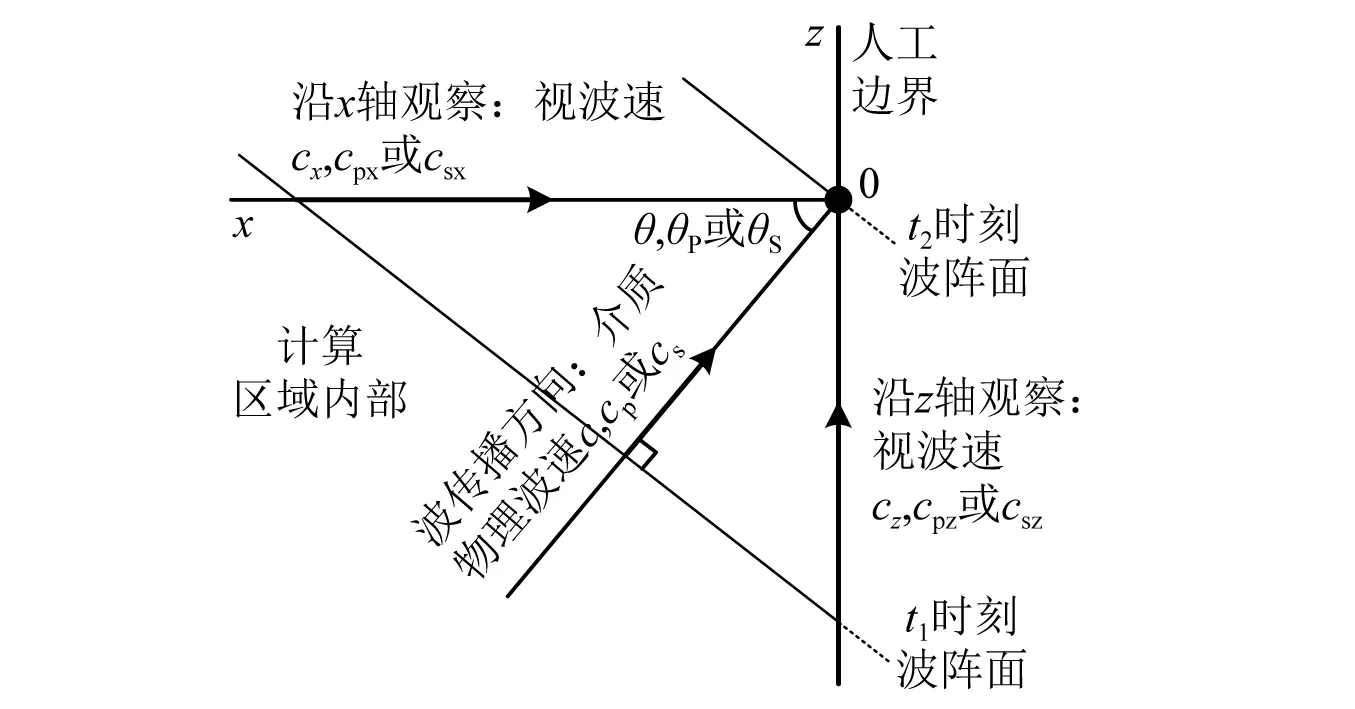
图5 平面波的透射角度与视波速Fig.5 Incident angles and apparent propagation velocities of plane waves

ΦP和ΦS为P波和S波势函数，则两组反射模式下边界附近的波场分别为

P波入射：P-P，P-S反射系数Rpp，Rps

ΦP=exp[i(ωt+kpxx+kpzz)]+Rppexp[i(ωt-kpxx+kpzz)]，

ΦS=Rpsexp[i(ωt-ksxx+kszz)]

(20)

S波入射：S-P，S-S反射系数Rsp，Rss

ΦP=Rspexp[i(ωt-kpxx+kpzz)],

ΦS=exp[i(ωt+ksxx+kszz)]+Rssexp[i(ωt-ksxx+kszz)](21)

波势函数ΦP，ΦS与数值模拟使用的波场分量u，w存在如下转换关系

(22)

此时caj-MTF的等价连续边界式 (19)的具体形式为

将式(20)代入式(22)，再将结果代入(23)，求解联立方程组，即可导出P波反射系数Rpp和Rps；同理，式(21)、式(22)和式(23)可以导出S波反射系数Rsp和Rss。

完成上述推导，最后得出P波入射产生P-P反射和P-S反射的反射系数Rpp和Rps为

(24)

(25)

S波入射产生S-P反射和S-S反射的反射系数Rsp和Rss为

(26)

(27)

式(24)～式(27)中同时含有θp和θs两个角度。在分析中，需要将Rpp，Rps表示成只含有θp的形式，将Rsp，Rss表示成只含有θs的形式。根据Snell定律：入射波、透射波和反射波沿界面的视传播速度相等，即cpz=csz(见图5)。于是得到关系式cp/sinθp=cs/sinθs，即

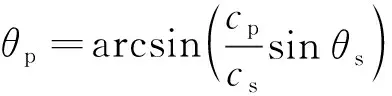
(28)

将式(28)第二式代入式(24)和式(25)，将式(28)第一式代入式(26)和式(27)，即为分析所用的两组(4种)弹性波反射系数。

3 边界反射特征及参数优化分析

图6绘出了16种情形下式(24)～式(28)各个弹性波反射系数的幅值曲线。这里考虑了两种弹性介质性质cp/cs=2和4，后者为大纵横波速比情形；两种边界阶次N=2和3，二阶边界最为常用，三阶边界也有一定应用；3种单一人工波速方案和一种多人工波速方案，前3种方案与现有MTF边界相同，最后一种方案是本文新型边界的特色。

人工边界的目标是实现对外行波的无反射，即所有反射系数在全部入射角范围内为零，但观察图6可知这种理想状况难以达到。不过，已有研究和数值试验表明，接近掠入射附近角度(如70°～90°)的波动能量通常少到可以忽略不计，因此反射系数只需在小角度和中等角度范围内(如0°～70°)足够小，就能给出接近理想的模拟结果。以此为考察标准，接下来结合图6，详细探讨弹性波情形下影响局部透射边界反射特征的三方面因素并进行参数优化分析。

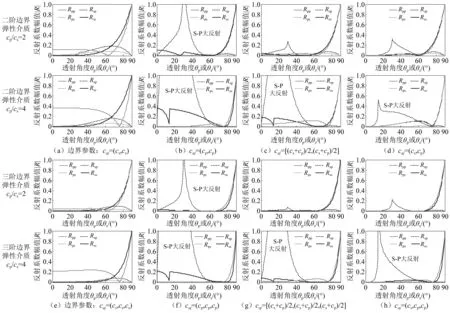
图6 弹性介质参数(cp/cs)和边界控制参数(N, caj) 不同取值情形下新型局部透射边界的弹性波反射系数Fig.6 Elastic-wave reflection coefficients of the new local transmitting boundary with different values of the elastic medium parameter cp/cs and the boundary control parameters N and caj

3.1 P，S两种物理波速波动能量的同步吸收

新型局部透射边界所具有的多人工波速参数正是为了更好地解决存在多种物理波速的复杂波动问题，尤其是当不同物理波速之间差异较大时，新边界比传统单一人工波速边界具有显著优势。

Xing等给出了caj-MTF对单分量波动(如声波或SH波动)的反射系数(基于等效表达式(19)导出)，通过将横坐标设置为视波速，很好地解释了新边界对多种物理波速波动能量的同步吸收。基于视波速的单分量波反射系数表达式为

(29)

式中，cn为外行波沿边界计算方向的视波速，根据图5，此时cn≡cx=ω/kx=v/cosθ，v为某种波动成分的物理波速，它可以是声波波速c、P波波速cp、S波波速cs等，θ为每种波的透射角度。式(29)针对局部透射边界模拟任意复杂波动问题的精度提供了一种无差别的度量标准，因此它比传统基于透射角度的单分量波反射系数更具一般性。

新型局部透射边界对P，S两种物理波速波动能量的同步吸收，可以通过将其中两个人工波速参数设定为ca1=cs和ca2=cp来实现(这对应于二阶边界)，对于更高阶边界的其余人工波速参数，可以在cs到略大于cp范围内取值。这种做法的原理是：根据式(29)，此时在cn=cs和cn=cp处为两个零反射点，零反射点附近的反射系数必然处于低值水平，因此在传播主要波动能量的垂直入射及其附近一定入射角范围内，P，S波都能够被很好地吸收。一阶边界只有一个人工波速参数，无法较好地兼顾对P波和S波的吸收；三阶边界能够进一步降低二阶边界两个零反射点附近的反射幅值，尤其是当P，S波速差异较大时，有必要使用它；更高阶边界继续提升精度的效果不明显，却更容易出现失稳问题，使用和讨论得很少。

类似地，利用本文给出的弹性波反射系数可以得出同样的结论。为证明这一点，可以将式(24)～式(27)改写成基于视波速cn的形式，并将其与式(29)的曲线绘制于同一幅图中，观察二者相似度。根据上述视波速定义，对于Rpp和Rps，cn=cp/cosθp，有θp=arcos(cp/cn)；对于Rsp和Rss，cn=cs/cosθs，有θs=arcos(cs/cn)。于是，式(24)～式(28)均可改写为关于变量caj,cn,cs,cp的形式。

为节省篇幅，这里不再写出基于视波速的弹性波反射系数表达式。图7给出了弹性波反射系数与单分量波反射系数绘制于同一坐标系的结果，三幅子图分别为一阶、二阶、三阶caj-MTF边界。图7中，v为某个可以被约去的速度值，用于将各个波速无量纲化。考虑cs=v，cp=3v，纵横波速比cp/cs=3。横坐标中视波速cn的值从v到6v，这涵盖了所关心的S波和P波从垂直入射到以小到中等角度入射的视波速范围。

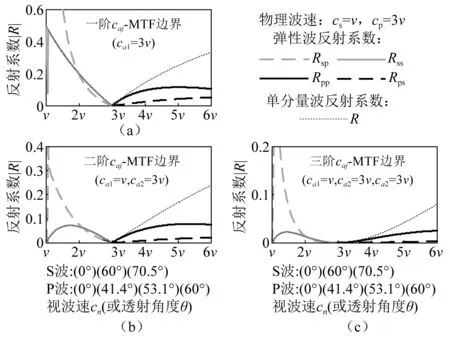
图7 基于视波速cn的弹性波与单分量波反射系数Fig.7 Elastic-wave and single-component-wave reflection coefficients in the context of the apparent velocity cn

在图7中，S波反射系数Rsp和Rss为灰色粗实线和虚线，位于坐标范围[v, 3v]，对应于θs从0°～70.5°(即arcos(v/3v))；P波反射系数Rpp和Rps为黑色粗实线和虚线，位于坐标范围[3v, 6v]，对应于θp为0°～60°(即arcos(3v/6v))；式(29)给出的单分量波反射系数R为细点线。总体上，弹性波曲线Rsp，Rss，Rpp，Rps所表示的整体反射特征与单分量波曲线R的变化规律基本一致，如：Rss与该段R完全重合；两类反射曲线具有共同的零反射点cn=v(即ca1)和cn=3v(即ca2)；Rpp与该段R在零反射点附近比较接近。这证明了就局部透射边界对于复杂波动问题中多种物理波速的处理而言，式(29)的确是一种简单可靠的度量标准。

图7中Rsp，Rss，Rpp，Rps的整体特征还存在几处与R不一致的地方：Rsp在一定范围内出现异常大值；Rpp不像该段R那样一直增大，而是先增大后下降；Rps的值要远小于该段R的值。这些差异是由P波和S波耦合效应引起的，它们可归结为附加零反射角和S-P大反射两方面因素。

3.2 附加零反射角和S波临界角

零反射角指边界反射系数为零的透射角度，前文将其称为零反射点(亦可称为零反射中心)。从图6和图7不难看出，在所关心的透射角度或视波速范围内，零反射点越多对边界精度越有利。

弹性波反射系数Rpp，Rps，Rsp，Rss有两种零反射角。一种是由边界参数caj所确定的，根据式(24)～式(27)乘号之前的部分计算，它们用视波速表述为cn=caj，若用透射角表述，则P波为cp/cosθp=caj，S波为cs/cosθs=caj。另一种是由弹性介质自身特性即纵横波速比cp/cs所确定的，根据式(24)～式(27)乘号之后的部分计算。本文将第二种角度称为弹性介质自身特性带来的附加零反射角，其值分别如下。

Rpp有一个附加零反射角θp0，其值根据式(30)确定

(30)

Rps有两个附加零反射角，为θp0=0°和90°；

Rsp有两个附加零反射角，为θs0=0°和90°；

Rss有一个附加零反射角θs0，其值根据式(31)确定

(31)

除了附加零反射角θp0和θs0之外，S-P反射中还有一种S波临界角θsc，对应于反射P波角度为临界状态90°的情形。根据式(28)第二式可得θsc为

(32)

式(30)～式(32)中θp0,θs0和θsc的值可用数值方法求解。图8绘出了它们的值随cp/cs的变化曲线。

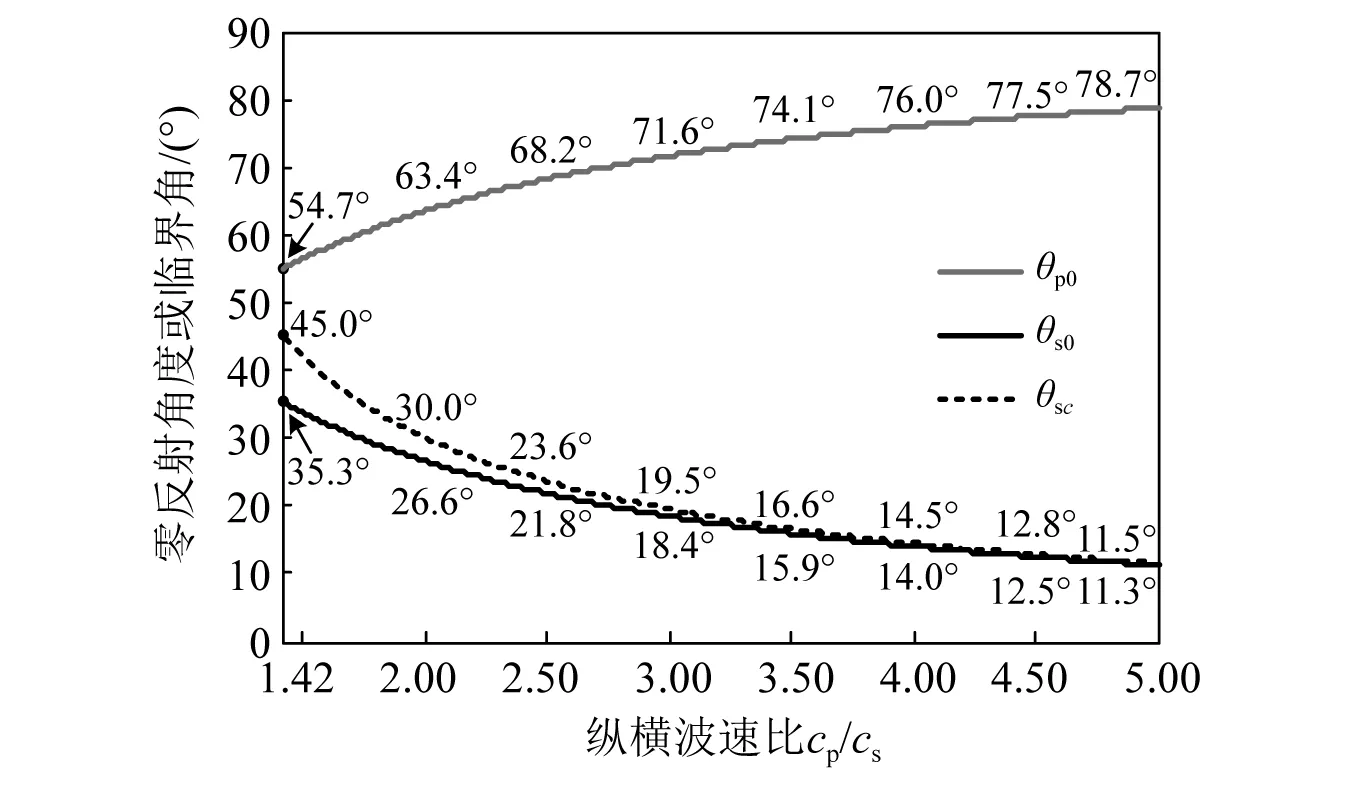
图8 Rpp,Rss的附加零反射角θp0,θs0以及S波临界角θscFig.8 The additional zero-reflection angles θp0, θs0 for Rpp, Rss and the S-wave critical angle θsc

图8中cp/cs=2和4处的附加零反射角θp0,θs0和S波临界角θsc都体现在图6的反射系数曲线当中，Rps和Rsp的两个附加零反射角0°和90°亦在其中。当cp/cs从1.42逐步变化到5时，Rpp的θp0从54.7°渐渐增大至78.7°，Rss的θs0从35.3°慢慢减小到11.3°，S波临界角从45°逐步减小至11.5°。θsc的值略大于θs0，二者差异随着cp/cs的增大而减小。了解这些角度值及其变化规律，有助于更好地掌握弹性波情形下局部透射边界的反射特征。一句话总结，由弹性介质自身特性带来的附加零反射角是对边界精度有利的因素。

3.3 S-P大反射问题

图6和图7曲线显示，S-P反射系数Rsp在S波临界角θsc附近一定范围内，常常会出现异常大值，其幅值可能达到接近甚至远超过1的程度。一旦出现S-P大反射，在主要波动能量所处的小角度及中等入射角范围内，常用的二阶或三阶边界的精度远不能令人满意，因此必须深入分析其原因并加以解决。

首先观察图6各幅子图，S-P大反射表现出以下特征：从左至右进行对比，人工波速caj全取为cs时未出现S-P大反射，其他参数情形均不同程度地出现了大反射，其中人工波速caj全取为cp时，异常大反射最为严重；S-P大反射在临界角θsc处有一个幅值尖峰，此角度附近的幅值迅速降低；从上往下对比，弹性介质纵横波速比cp/cs=4时的S-P大反射比cp/cs=2时严重得多，而三阶边界与二阶边界的区别在于新增一个反射因子(注：反射因子指式(24)～式(27)中相乘的每一项)所带来的乘积效应。

然后分析反射系数Rsp表达式(26)，并与Rpp，Rps，Rss的式(24)、式(25)、式(27)进行比较。最容易看出的是式(26)中存在一个放大因子cp/cs，纵横波速比越大，其对Rsp幅值的放大作用越显著；与之相反，式(25)中这个因子为cs/cp，对Rps幅值有缩小作用；式(24)和式(27)中没有类似因子。另一个比较直观的观察是caj/cs的值要大于caj/cp，而在Rsp中出现了前者位于分子后者位于分母的组合，导致其反射因子的幅值较大，可能达到接近甚至远超过1的水平；与之相比，Rpp，Rps，Rss的各个反射因子中均没有类似组合。这两个直观观察粗略地解释了Rsp有时会出现异常大反射，而Rpp，Rps，Rss均没有类似问题的原因。

为严谨起见，进一步对Rsp表达式(26)进行定量分析。S-P大反射的幅值在S波临界角θsc(见式(32)和图8)处有一个尖峰，图6未充分显示其幅值变化规律，这里对其进行探究。将θsc代入式(26)，得到此处Rsp的值为

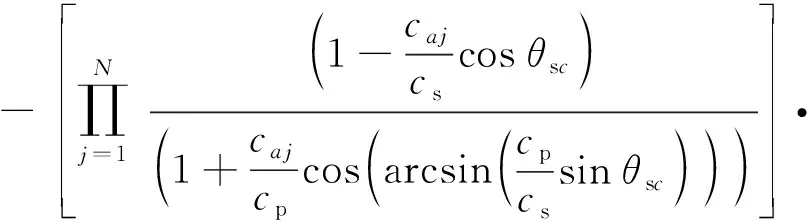
(33)

图9绘出了式(33)在不同边界参数caj(j=1,…,N)取值下，各个反射因子的幅值及其组合得到的S-P反射的峰值Rsp(θsc)随着纵横波速比cp/cs的变化。

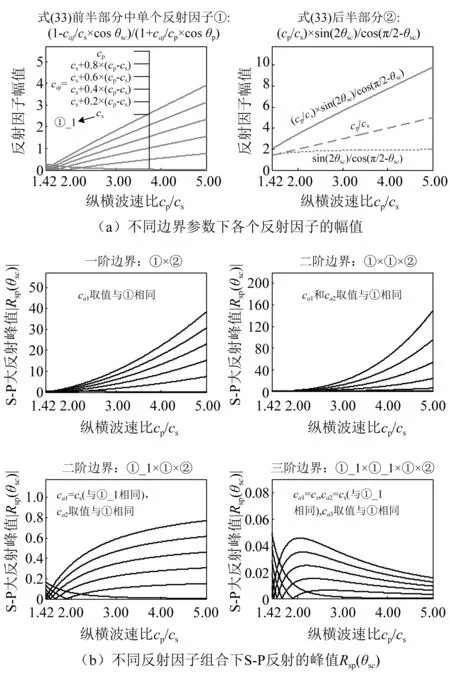
图9 S-P大反射峰值分析Fig.9 Analysis of the peak value of S-P large reflection

图9从定量角度严格证明了上述基于直观观察对S-P大反射原因做出的解释。具体为：图9右上角子图显示，sin(2θsc)/cos(π/2-θsc)提供了幅值接近于2的基础性放大贡献，参数cp/cs是逐步增长的放大倍数，二者组合形成一个幅值约为2～10 (考虑cp/cs从1.2变化到5.0)的反射因子；左上子图显示，式(33)前半部分中各个反射因子的幅值随着cp/cs的变化有可能达到远超过1的水平，这是由于caj/cs位于分子caj/cp位于分母所造成的。S-P反射的峰值为这些反射因子的乘积，当后者都远超过1时，会导致峰值Rsp(θsc)出现极大的异常值，如几十至数百。

解决S-P大反射问题的方法已经由基于图6的直观观察和图9的定量分析所暗示：只要将所有人工波速参数严格设定为S波波速，即caj=cs(j=1, …,N)，就不会出现S-P大反射。其原理为：图9左上子图显示当caj=cs时，式(33)前半部分中反射因子的幅值接近于零，若干个这样因子的乘积能够有效地抵消后半部分天然具有的约为2～10的大幅值，从而使得S-P反射峰值Rsp(θsc)降至人工边界精度所要求的低值水平(如小于0.1)。

但是，上述解决S-P大反射问题的边界参数取值方案与3.1节所给出的解决P和S两种物理波速问题的方案存在冲突，后者要求至少有两个caj参数取值为caj=(cs,cp)。从图9左上子图可知，caj=cp的反射因子幅值能够达到1～3左右(考虑cp/cs位于2～4)。此时，为了抵消这个因子和后半部分因子的大幅值，需要至少两个caj=cs的反射因子，这对应于控制参数为caj=(cs,cs,cp)的三阶局部透射边界。这种参数配置在图6中没有出现，表明Xing的研究基于单分量波反射系数式(29)所建议的三阶边界参数caj= (cs,cs,cp)在弹性波情形下并不是好的选择。图10给出了本文建议的caj=(cs,cs,cp)三阶边界的弹性波反射系数。

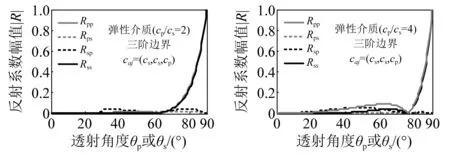
图10 参数为(cs, cs, cp)的三阶边界的弹性波反射系数Fig.10 Elastic-wave reflection coefficients of the 3rd-order boundary with parameters of (cs, cs, cp)

与图6各幅子图比较可知，图10边界方案效果更好，它既实现了对P和S波的同步吸收，又不存在S-P大反射问题。进一步研究发现，避免S-P大反射的方法可以退化为：只需将大部分(如1/1, 2/2, 2/3, 3/4, 3/5, …)人工波速参数严格设定为S波波速，就可以避开这个问题。

最后需要指出，现有局部透射边界最常使用的是二阶形式，但各种参数方案下的二阶边界都无法同时兼顾对P,S波的同步吸收与避开S-P大反射两个方面。不过，根据上述理论分析并观察图6和图9曲线，可以给出二阶边界的使用建议如下：可用于纵横波速比不大(如cp/cs不超过2.5)的弹性介质；优先考虑采用caj=(cs,cp) 作为边界参数；严格避免使用参数方案caj=(cp,cp)；理论上无法实现对各种波动成分的完美吸收，对于纵横波速比不大的问题，能给出较高精度模拟结果。除此之外，对于纵横波速较大(如cp/cs>2.5)的问题，则建议使用图10给出的(cs,cs,cp)三阶边界。由于岩土介质的力学性质常常以泊松比υ来表述，为便于了解大纵横波速比cp/cs所对应的岩土介质类型，图11绘出了υ与cp/cs的关系曲线。

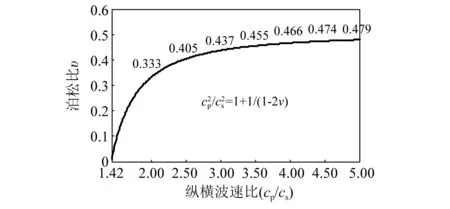
图11 弹性介质泊松比与纵横波速比的关系Fig.11 The relation of Poisson’s ratio and the ratio of longitudinal and transverse velocities in elastic media

图11表明，局部透射边界S-P大反射问题比较突出的大纵横波速比弹性介质，比如cp/cs>2.5，其泊松比范围为υ∈(0.405, 0.500)。河谷、湖泊、沉积盆地、海洋沉积物等软土介质经常能够达到这么大的泊松比。因此，当基于弹性波方程来模拟这类介质中的地震波传播时，需要采用本文提出的理论与方法来提高局部透射边界的精度，确保模拟结果合理性。在当前大型沉积盆地上的城市抗震安全、海洋地震工程等重要问题受到广泛关注的背景下，本文工作有着巨大应用和推广价值。

4 算例验证

4.1 均匀介质波源问题

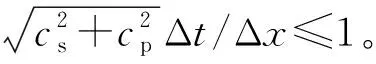
图12、图13分别为cp/cs=2,cp/cs=4两种弹性介质在不同边界参数下的模拟结果。图12、图13给出了水平分量u在两个典型时刻的波场快照，其中1.5 s，0.85 s为P波穿过边界，2.6 s，2.4 s为S波穿过边界。

图12 不同边界参数对cp/cs=2弹性介质的模拟结果Fig.12 Modeling results of elastic waves (cp/cs=2) using different boundary parameters

图13 不同边界参数对cp/cs=4弹性介质的模拟结果Fig.13 Modeling results of elastic waves (cp/cs=4) using different boundary parameters

图12、图13给出的边界反射规律与图6、图10的反射系数曲线及第3章理论分析结果完全相符。主要包括：所有单一人工波速方案都无法很好地实现对P波和S波的同步吸收，而含有caj=(cs,cp)的多人工波速方案能够做到。小纵横波速比(cp/cs=2)弹性介质仅在边界参数为(cp,cp)和(cp,cp,cp)时出现了轻度的S-P反射问题，但大纵横波速比(cp/cs=4)弹性介质出现了极其严重的S-P大反射。(cp,cp)和(cp,cp,cp)方案最容易出现S-P大反射且幅值最大；(cs,cs)、(cs,cs,cs)，(cs,cs,cp)这几种caj=cs数目占优势的方案都没有出现S-P大反射。值得注意的是，在图12中表现良好的(cs,cp,cp)方案(Xing等推荐的三阶边界方案)，在图13中也出现了显著的S-P反射误差。在图12和图13中，本文所建议的(cs,cs,cp)方案三阶边界均给出了非常满意的结果。

图14绘出了cp/cs=4介质模拟中(x,z)=(300 m, 500 m)处观察点的u分量时程及其边界反射误差。此处提取了6种参数方案下的结果，已在图13中用倒三角形示出。在计算边界反射误差时，以(cs,cs,cp)方案作为参考解。

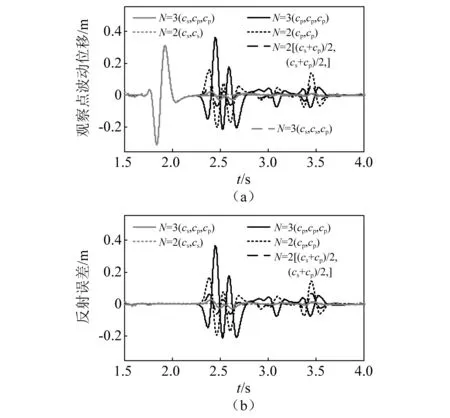
图14 观察点的u分量时程及边界反射误差(cp/cs=4)Fig.14 Time histories of the component u at the observation point and their boundary-reflection errors (cp/cs=4)

图14结果显示，一些参数方案下u分量的边界反射误差会达到接近甚至超过入射波幅值的程度，这远远超出了人工边界条件所能接受的合理误差范围。这表明在大纵横波速比介质(cp/cs=4)弹性波模拟中，S-P大反射对边界精度具有严重破坏作用，必须采用本文所提出的方案来避开这个问题。

另外需要指出，图14给出的u分量反射误差并未达到如图9所示的数十倍以上的程度。这种差异具有合理性，因为：反射系数Rsp是关于波势函数ΦP和ΦS的，u分量与它们存在转换关系式(22)；反射系数基于平面谐波给出，而本试验为暂态的短持时脉冲波；最重要的原因是图9给出的是S-P反射在临界角θsc处的峰值Rsp(θsc)，临界角附近的S-P大反射幅值会迅速降低(参考图6)，本试验中的S波入射角与临界角不同。总之，第3章的理论内容很好地预测了此处数值试验结果。

4.2 自由地表散射问题

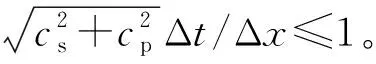
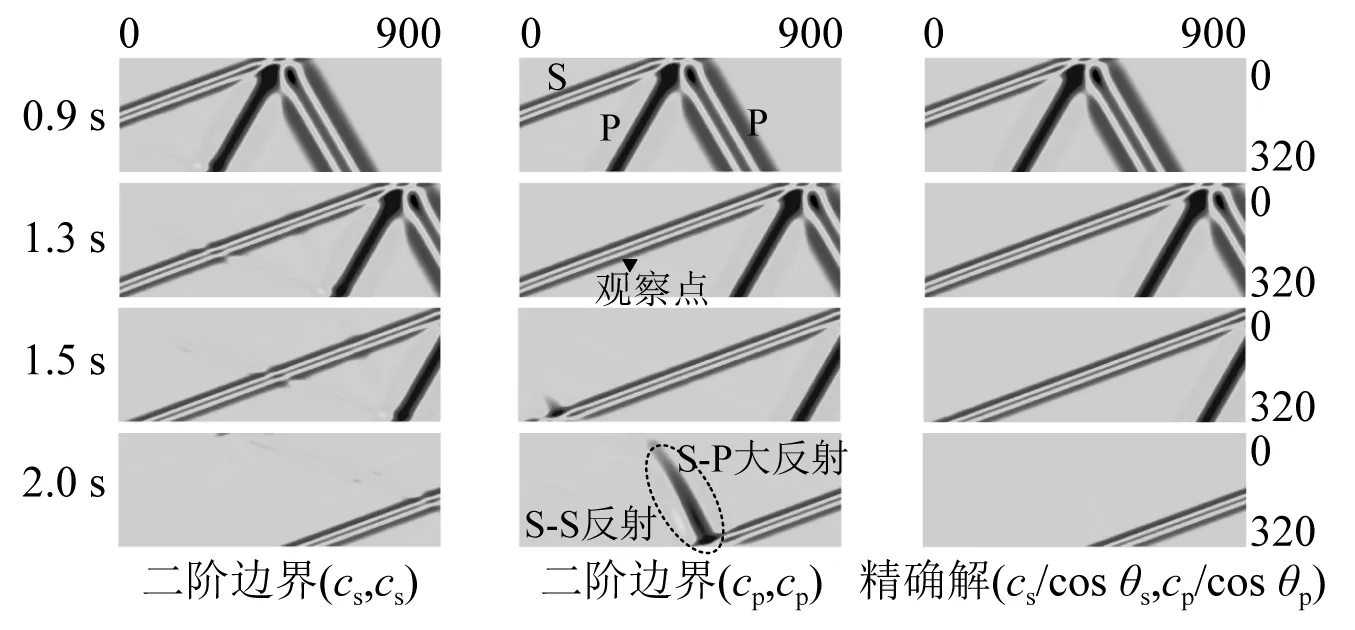
图15 散射问题波场快照(u分量)Fig.15 Snapshots of a scattering problem (u component)

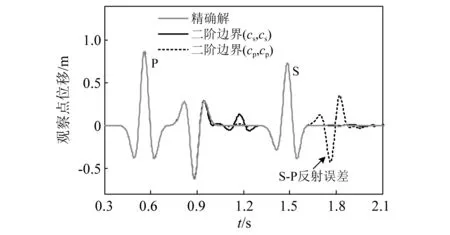
图16 (x, z)=(300 m, 240 m)处观察点的u分量时程Fig.16 Time histories of the component u at the observation point (x, z)=(300 m, 240 m)

图15中右侧边界对于两道P波和一道S波实现了完美的同步吸收，表明对于这种视波速可以事先确定的情形，局部透射边界效果极佳。在底部边界上，(cs,cs)边界很好地吸收了S波而对P波有明显反射，(cp,cp)边界很好吸收了P波而对S波有很大反射，基于视波速的边界精确解则实现了对两种波的同步吸收。观察(cp,cp)边界的反射，S波反射分为S-P和S-S两道，S-P反射的幅值要远远大于后者。从图16可以进一步看出，(cp,cp)方案S-P反射造成的误差很大，是影响模拟结果的最重要因素。在短持时脉冲波模拟结果中，不合理的边界方案尚且出现如此显著的误差，对于长持时的地震波模拟，更应注意采用合理的边界方案来确保边界精度。

4.3 复杂不均匀介质问题

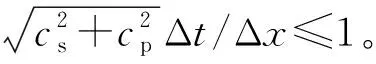
图17 复杂不均匀介质模型Fig.17 A model of complicated heterogeneous media

图18为3组模拟得到的波场快照。结果表明：自由边界会将外行波完全反射回计算区域，其模拟结果与实际无限介质中的波传播过程相去甚远。(cp,cp,cp)边界在左侧和右侧边界上都出现显著的大反射(根据前文理论可知此为S-P大反射)，严重影响了模拟结果的可用性。据此以推断对于长持时的实际地震波问题，边界反射误差不断叠加累积，会导致更加不合理的结果。(cs,cs,cp)边界很好地消除了人工边界上的虚假反射波，说明它所推算的各个人工边界节点的运动比较符合实际无限介质问题中该处的运动，所以有限模型的模拟结果再现了实际波动过程。

图18 不均匀介质弹性波模拟结果Fig.18 Modeling results of elastic waves in heterogeneous media

5 结 论

通过将多个人工波速参数引入廖氏透射边界的算子表达式，提出一种优化的新型局部透射边界，并给出简洁实用的数值计算格式。新边界比廖氏透射边界更具一般性，后者为前者多个人工波速取相同值的特例。局部透射边界对弹性波的反射特征受到P波与S波耦合效应的重要影响，但现有透射边界理论所给出的基于单分量波(如声波或SH波)的反射系数或“误差波多次透射”的物理机制并未考虑这个效应。本文给出了弹性波情形下局部透射边界的两组(4种)反射系数Rpp，Rps和Rsp，Rss的明确定义，推导出反射系数的严格表达式，据此详细探讨了边界反射特征并进行参数优化分析。理论与数值试验相结合，得到以下研究结论：

(1) 新型局部透射边界具有的多个人工波速配置能够比现有基于单一人工波速的透射边界更好地处理含有多种物理波速的复杂波动问题。当一组人工波速取值中同时含有P波和S波波速时，新边界能够很好地实现对这两种波的同步吸收。

(2) 弹性波反射系数中除了由边界参数决定的零反射角之外，还存在由P波与S波耦合效应(弹性介质自身特性)带来的附加零反射角。零反射角越多，在0°～90°内分布越均匀，边界精度越好。

(3) 在纵横波速比较大(如cp/cs>2.5)的弹性介质中，S-P反射系数Rsp有时会出现幅值接近甚至远超过1的异常放大，这会严重破坏边界精度。不过，当大部分(如1/1, 2/2, 2/3, 3/4, 3/5, …)人工波速参数被严格设定为S波波速时，就不会出现S-P大反射问题。

(4) 局部透射边界S-P大反射问题比较突出的大纵横波速比介质(如cp/cs>2.5)，其泊松比范围为v∈(0.405, 0.500)，河谷场地、沉积盆地、海洋沉积物等软土介质通常具有较大泊松比。因此，当基于弹性波方程来模拟这类介质中的地震波传播时，需要采用本文方法来提高边界精度，确保模拟结果的合理性。在目前大型沉积盆地上的城市抗震安全、海洋地震工程等受到广泛关注的背景下，本文工作有着巨大应用和推广价值。

Vol．41 No．12 2022