振速轴向不一致下矢量传感器阵列方位估计方法

王伟东， 李向水， 谭伟杰， 邹波蓉， 李 辉

(1. 河南理工大学 物理与电子信息学院，河南 焦作 454000；2.贵州大学 大数据产业发展应用研究院 公共大数据国家重点实验室，贵阳 550025)

随着隐身技术的不断发展，借助消声瓦新型材料，武器装备，例如鱼雷、水雷、水面舰等，辐射噪声的频率与强度逐年降低，给被动探测设备带来了困难[1-2]。为了提高远程低频目标的方位估计性能，通常需要增加声压传感器阵列的孔径。然而，对于空间受限的探测平台，想要增加阵列的孔径通常是比较困难的。矢量传感器阵列是解决上述难题的理想方案。较之仅能测量声场中声压信息的声压传感器，矢量传感器能共点、同步、独立地测量声场中的声压和振速信息，通过测量的声压和振速信息可实现全空间范围内目标方位角的无左右舷模糊估计[3-4]，为空间受限平台探测系统进行远程低频目标的探测奠定了基础。

Nehorai等[5]利用克罗内克乘积将矢量传感器及其阵列信号模型与传统的声压传感器阵列信号模型统一以来，基于已日趋成熟的声压传感器阵列方位估计方法，如声能流方法、波束形成方法[6]、高分辨子空间类方法[7-8]等，广泛被应用矢量传感器阵列的目标方位估计中。声能流方法及波束形成方法具有结构简单、计算量小的优势，但是两种方法的分辨性能较差。子空间类方法，诸如多重信号分类(multiple signal classification, MUSIC)方法[9]和旋转不变技术估计信号参数方法[10]及它们的改进方法[11-12]，通过利用信号子空间和噪声子空间的正交性突破了波束形成方法无法实现一个波束范围内两目标的分辨这一弊端，实现了目标的高分辨方位估计。然而，该类方法对信号子空间与噪声子空间的正交性具有较强的敏感性使其处理相干信号时方位估计性能急剧下降。在传统的声压传感器阵列信号处理中，空间平滑技术[13]是解决相干信号方位估计的有效方法之一。在阵列孔径较大时，该方法能够被应用于矢量传感器阵列的相干信号处理中。但是，空间平滑技术是以损失阵列的孔径为代价来提高相干信号的方位估计性能。为了解决此难题，文献[14-16]利用矢量传感器固有的指向性，相继提出了振速域平滑方法、振速域差分平滑方法及无左右舷模糊的平滑方法。相较于空间平滑技术，尽管振速类平滑方法在未损失阵列孔径的前提下提高了相干信号源的方位估计性能，但是，矢量传感器阵列面临损失自由度的难题。

稀疏信号处理方法是最近十几年兴起的方位估计方法。早期，多数稀疏表示方位估计方法[17-18]是基于声压传感器阵列进行的研究。该类算法对信号之间相关性的敏感度较低，被应用于矢量传感器阵列方位估计时能解决矢量传感器阵列损失自由度的难题。国内外学者对矢量传感器阵列稀疏表示方位估计方法的研究成果并不多见。针对低信噪比和小快拍下高速运动目标的稳健高分辨方位估计问题，文献[19]提出了基于矢量传感器阵列的稳健高分辨方位估计方法。然而，该方法的方位估计性能受噪声功率门限值影响较大。此外，该方法涉及到声压与振速的互相关操作，导致矢量传感器阵列损失自由度的难题。针对各向同性环境噪声下矢量传感器阵列相干信号方位估计性能下降问题，文献[20]提出了基于增广互协方差矩阵矢量稀疏表示的方位估计方法。尽管该方法的估计精度有所提升，但是矢量传感器阵列损失自由度的难题依然存在。为了解决小孔径矢量传感器阵列损失自由度的难题，文献[21]提出了稀疏信号功率迭代补偿的矢量传感器阵列方位估计方法。在该方法中，当前一次迭代估计的稀疏信号功率是基于前一次稀疏信号功率的估计结果进行的补偿，提高了矢量传感器阵列在信噪比较低和角度间隔较小时的方位估计性能。

然而，上述方法都是基于阵列中振速轴指向同一方向的理想假设，对矢量传感器阵列的方位估计性能进行的研究。由于矢量传感器具有偶极子指向性，在安装矢量传感器阵列时，难以保障阵列中的振速轴指向同一方向，简称为振速轴向不一致，使矢量传感器阵列的方位估计性能下降。文献[22]在矢量传感器阵列信号模型中引入了一个轴向角度偏差参数，在迭代自适应方法(iterative adaptive approach，IAA)的基础上建立了关系稀疏信号和轴向偏差矩阵的代价函数。然后提出了一种交替迭代自适应方法(alternating iterative adaptive approach，AIAA)，该方法基于贝叶斯信息准则对信号进行补偿，进一步提高了轴向偏差参数偏差模型下矢量传感器阵列的方位估计精度。然而，该方法是基于矢量传感器阵列输出的一阶统计量进行的研究。相较于一阶统计量，矢量传感器阵列输出的二阶统计量具有更多的自由度和输出信噪比。

因此，针对振速轴向不一致时矢量传感器阵列方位估计性能恶化问题，提出了一种两步加权交替迭代方法(two-step weighted alternating iterative approach, TWAIA)。首先，基于矢量传感器阵列的二阶统计量，采用正则化加权协方差矩阵拟合方法估计稀疏信号功率。其次，采用正则化加权最小二乘估计轴向角度偏差矩阵。在每次迭代中，为了提高稀疏信号功率在空域的稀疏性，稀疏信号功率补偿项被约束；为了消除轴向角度偏差对方位估计性能的影响，基于矢量传感器固有的指向性，期望的轴向角度偏差矩阵被重构。仿真结果表明，与现有方法相比，该方法提高了振速轴向不一致时矢量传感器阵列的方位估计精度。

1 问题描述

1.1 理想矢量传感器阵列数据模型

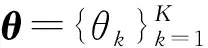
h(θk)=[1 cosθksinθk]T

(1)

式中，θk∈(-180°,180°]为第k个信号源的水平方位角。

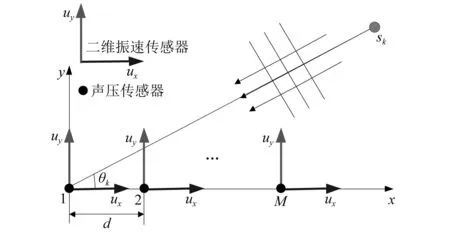
图1 理想矢量传感器均匀线阵模型Fig.1 The ideal uniform vector sensor array model

于是，由M个矢量传感器组成均匀线列阵的阵列流形矩阵为

A(θ)=[a(θ1),…,a(θK)]=

[ap(θ1)⊗h(θ1),…,ap(θK)⊗h(θK)]=

Ap(θ)⊙H(θ)

(2)

式中:Ap(θ)=[ap(θ1),ap(θ2),…，ap(θK)]为声压传感器阵列的阵列流形矩阵；H(θ)=[h(θ1),h(θ2),…，h(θK)]为各声源在单矢量传感器上的响应；ap(θk)=[1,…,e-j2π(M-1)dcos θk/λ]T为第k个声源在声压传感器阵列上的响应；a(θk)为第k个声源在矢量传感器阵列上的响应；λ为声波的波长；⊗为Kronecker积；⊙为Khatri-Rao积。于是，矢量传感器阵列在t时刻的输出矢量为

Y=A(θ)S+W

(4)

式中:Y=[y(1),y(2),…,y(L)]；S=[s(1),s(2),…,s(L)]；W=[w(1),w(2),…,w(L)]。

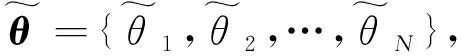
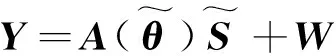
(5)

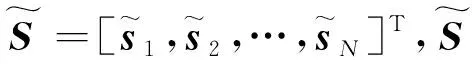
1.2 振速轴向不一致时矢量传感器阵列模型

由于矢量传感器本身固有的偶极子指向性，在安装矢量传感器阵列时通常会存在轴向角度偏差，即阵列中的振速轴没有指向同一个方向，如图2所示，其中，βm为第m个矢量传感器的轴向角度偏差，β=[β1,β2,…,βM]T为矢量传感器阵列的振速轴向偏差矢量。

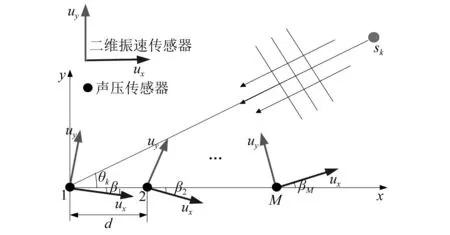
图2 振速轴向不一致下矢量传感器均匀线列阵模型Fig.2 The uniform vector sensor array model with velocity axial inconsistency

因此，当第k个声源入射在第m个矢量传感器上时，式(1)可修正为

h(θk,βm)=[1·cos(θk-βm) sin(θk-βm)]T=

gmh(θk)

(6)

式中，gm为第m个矢量传感器的轴向角度偏差矩阵

(7)

振速轴向不一致下第k个声源在矢量传感器阵列上可表示为

a(θk,β)=[ap(θk)⊗h(θk,β1),…,ap(θk)⊗h(θk,βM)]=

[a1p(θk)g1h(θk),…,aMp(θk)gMh(θk)]=

GAp(θk)F(θk)

(8)

式中:Ap(θk)=diag{apk⊗I3×1}；diag{·}为对角矩阵操作；apk=[a1k(θk),…,aMk(θk)]T；F(θk)=IM×1⊗h(θk)；Ii×1为i行的单位矢量；G为矢量传感器阵列的轴向角度偏差矩阵

G=blkdiag{g1,g2,…,gM}

(9)

式中，blkdiag{·}为块对角矩阵操作。

振速轴向不一致下，矢量传感器阵列的稀疏矢量数据模型式(5)，可修正为

(10)

2 两步加权交替迭代自适应矢量传感器阵列方位估计方法

根据式(10)，在无噪声情况下，第n个网格相应的信号协方差矩阵可表示为

(11)

(12)

于是，相应于第n个网格上信号的干扰加噪声协方差矩阵为

Σn=R-Rn

(13)

式中，R为信号加噪声协方差矩阵，

(14)

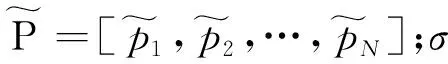
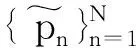
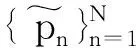
(15)

其中

(16)

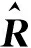
G(j+1)=arg minFG(G)

s.t.GGH=GHG=I

(17)

其中

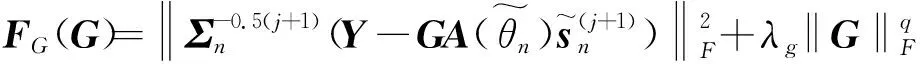
式中：λg为正则化参数，平衡着轴向角度偏差矩阵与拟合误差之间的关系。

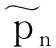
2.1 估计稀疏信号功率

假设F(x)=xq是关于变量x的函数。不难看出，F(x)也是关于变量x的凹函数。当变量x>0时，根据文献[24]可知，对于变量x0>0，可得

F(x)≤F(x0)+F′(x0)(x-x0)

(19)

(20)

(21)

(22)

(23)

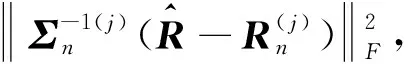
(24)

其中

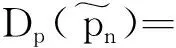
(25)

(26)

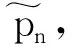
(27)

其中

(28)

(29)

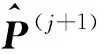
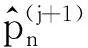
(31)

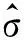
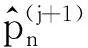
(32)

(33)

对式(27)的解析表达式和所提算法的收敛性进行推导。

(1)式(27)的证明

(34)

其中

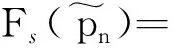
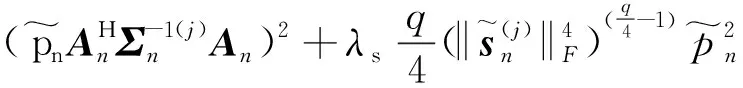
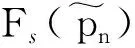
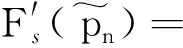
(37)

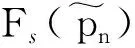
(39)

其中

(40)

从式(39)中可以看出，在计算N个离散网格上对应的稀疏信号功率时，共需计算N次干扰加噪声协方差矩阵Σn的逆，因此，计算量较大。为了减少干扰加噪声协方差矩阵Σn的逆运算，根据Woodbury公式，可得

(41)

其中

(42)

把式(41)代入式(39)，可得

(43)

其中

(44)

证毕。

(2)收敛性证明

易看出，若是所提方法具有收敛性，需要满足如下条件

(45)

式(45)的证明过程如下。

(46)

根据式(16)、式(24)及式(25)，可知

(47)

(48)

根据式(46)、式(47)和式(48)，可得式(45)是成立的。因此，所提算法具有收敛性。

证毕。

2.2 估计轴向角度偏差矩阵

类似于式(15)到式(26)的转化，式(16)同样可以转化为关于轴向角度偏差矩阵G的线性函数，即最小化式(16)关于轴向角度偏差矩阵G等价于最小化下式，

G=arg minH(G)
s.t.GGH=GHG=I

(49)

其中

(50)

为了解决式(49)的优化问题，首先通过最小化式(50)获得轴向角度偏差矩阵G的粗略估计。然后，利用矢量传感器固有的方向性，对粗略估计的轴向角度偏差矩阵进行重构使其满足期望的轴向角度偏差矩阵。可以看出，通过最小化式(50)求解的轴向角度偏差矩阵粗略估计是与所有网格上相应的来波方向有关系的，为了进一步提高轴向角度偏差矩阵的估计精度，仅利用与K个目标方位对应的信号求解轴向角度偏差矩阵。则式(50)进一步转化为

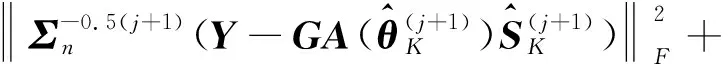
(51)

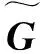
(52)

其中

(53)

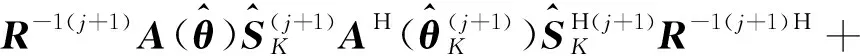
(54)

2.3 重构期望的轴向角度偏差矩阵

(55)

式中，η=3m-1。假设第m个矢量传感器的振速轴向作为参考方向，可求得相对轴向角度偏差矩阵为

(56)

则估计的第m个矢量传感器的指向性角度偏差可表示为

(57)

(58)

则矢量传感器阵列的轴向角度偏差矩阵可表示为

(59)

式中，轴向角度偏差矩阵初始化为

(60)

2.4 所提算法总结

所提算法总结如下。

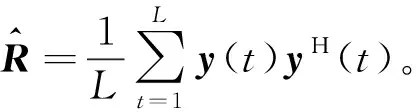
第三步：根据式(30)，更新R(j)。

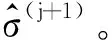
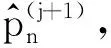
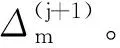
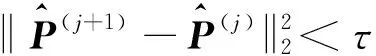
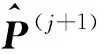
2.5 所提算法计算复杂度分析

对所提TWAIA算法计算复杂度进行分析，这里假设迭代次数为Titer(Titer≤Tmax)。所提算法初始化部分需MN+(2L+1)N次乘法与MN+(2L-1)N次加法，计算协方差矩阵R的逆需M2N+MN+21M3次乘法与M2N+21M3次加法，计算网格上对应稀疏信号功率需7M2N+5MN+3N次乘法与6M2N+2MN+2N次加法，估计和重构轴向角度偏差矩阵需12M2N+3MN+KN次乘法与4M2N+MN次加法。所提算法的计算量为O{31TiterM2N+(12Titer+2)MN+(5Titer+4L)N+TiterKN+42M3}。MUSIC不需要进行逆矩阵和迭代运算，计算量为O{M2L+M3N}。SAMV-1和AIAA的计算量分别为O{15TiterM2N+(5Titer+2)MN+(2Titer+4L)N+42M3}和O{(13Titer+2)M2N+(8Titer+7)MN+(3Titer+2L)MN+TiterKN+42M3}。因此，相较于MUSIC，IAA和AIAA算法，所提TWAIA算法具有较高的计算量，但是在比较的几种方法中，TWAIA算法的方位估计精度是最高的。

3 仿真与性能分析

在本章中，将所提TWAIA方法与经典的 MUSIC方法、SAMV-1方法及AIAA方法进行比较，评估所提方法的有效性与稳健性，同时给出了矢量传感器阵列的克拉美罗下界(Cramer-Rao lower bound, CRLB)曲线，以此作为比较的基准。所有方法都是基于一个由M元矢量传感器组成的均匀线列阵进行的研究，并且相邻阵元间的间距为一个波长。除了位于坐标原点处矢量传感器的振速轴方向作为参考之外，在每次蒙特卡洛仿真中，其它矢量传感器的振速轴向相较于参考阵元的轴向角度偏差满足均值为β，方差为ρ2的均匀分布。等功率远场窄带不相干的信号为复指数信号，其中心频率f=711 Hz，系统采样频率为fs=8 kHz，声源的角度扫描范围为[-180°∶2°∶180°]。在所提方法中，τ=1×10-3，Tmax=20，根据Wang等的研究和文献[27]的分析，υ=45，λs=λg=0.625，q=0.5。下文仿真中把均方根误差作为估计精度的衡量标准，并定义均方根误差(root mean square error, RMSE)为

(61)

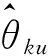
试验一：均方根误差与信噪比的关系

假设两个等功率远场不相干的信号源入射在矢量传感器阵列上，图3给出了两个信号源的方位角分别位于θ1=-14°，θ2=38°，阵元个数为4，快拍数为300，β=15，ρ=4时，均方根误差与信噪比的关系。从图3可以看出，随着信噪比的增加，MUSIC的均方根误差相较于CRLB具有较大的间隔，且MUISC的均方根误差变化趋势较缓慢，这主要是由于MUSIC未考虑轴向角度偏差对矢量传感器阵列方位估计的影响。尽管SAMV-1方法也未考虑轴向角度偏差对矢量传感器阵列方位估计的影响，但是相较于MUSIC方法，SAMV-1方法与CRLB之间的间隔有所减小，这表明SAMV-1方法对矢量传感器阵列轴向角度偏差具有较低的敏感性。相较于MUAIC方法和SAMV-1方法，尽管AIAA通过估计轴向角度偏差矩阵对观测数据进行了校准，减小了它对目标方位角度估计性能的影响。显著的是，AIAA方法在信噪比较高时，它的估计性能接近于CRLB，但在信噪比较低时，它的估计性能仍较差。这主要是由于AIAA方法在估计稀疏信号时是根据阵列的一阶统计特性进行的估计，加之轴向角度偏差矩阵采用最小二乘估计未考虑轴向角度偏差矩阵与残差之间的关系导致AIAA方法在低信噪比时方位估计精度不高。相反，所提方法的均方根误差与CRLB之间具有较小的间隔，这主要归因于所提方法是依据矢量传感器阵列输出的二阶统计量估计稀疏信号功率，并且采用正则化加权最小二乘估计轴向角度偏差矩阵，并通过户用参数较好的平衡了信号在空域的稀疏性及轴向角度偏差矩阵与残差之间的关系，使得所提方法在低信噪比下矢量传感器阵列的方位估计精度得以提高。

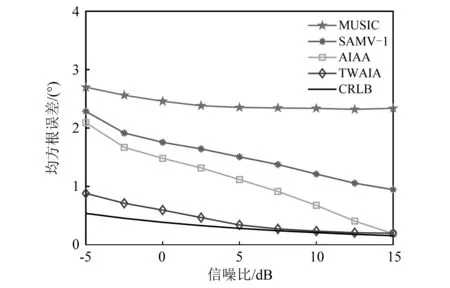
图3 均方根误差与信噪比的关系Fig.3 RMSE versus SNR

试验二：均方根误差与快拍数的关系

图4比较了均方根误差与快拍数的关系，除了信噪比为8 dB、快拍数在[20，40，60，80，100∶100∶600]内变化之外，其他仿真参数的设置与图3保持一致。从图4中可以看出，不论快拍数较小还是较大，MUSIC方法的均方根误差都较大。相较于MUSIC方法，尽管SAMV-1方法的估计精度有很大提升，但是与CRLB之间仍有较大的间隔。在快拍数小于40时，AIAA方法方位估计性能恶化，这主要是由于在快拍数较小时，恢复的稀疏信号不够精确，导致最终估计的稀疏信号功率误差较大，从而致使方位估计误差较大。所提方法依据矢量传感器阵列输出的二阶统计量估计稀疏信号功率，并采用正则化参数及用户参数进行约束有效的提高了快拍数不足时AIAA方法存在的弊端，并且当快拍数充足时所提方法的均方根误差曲线近似于CRLB，表明了所提方法具有较好的方位估计性能。

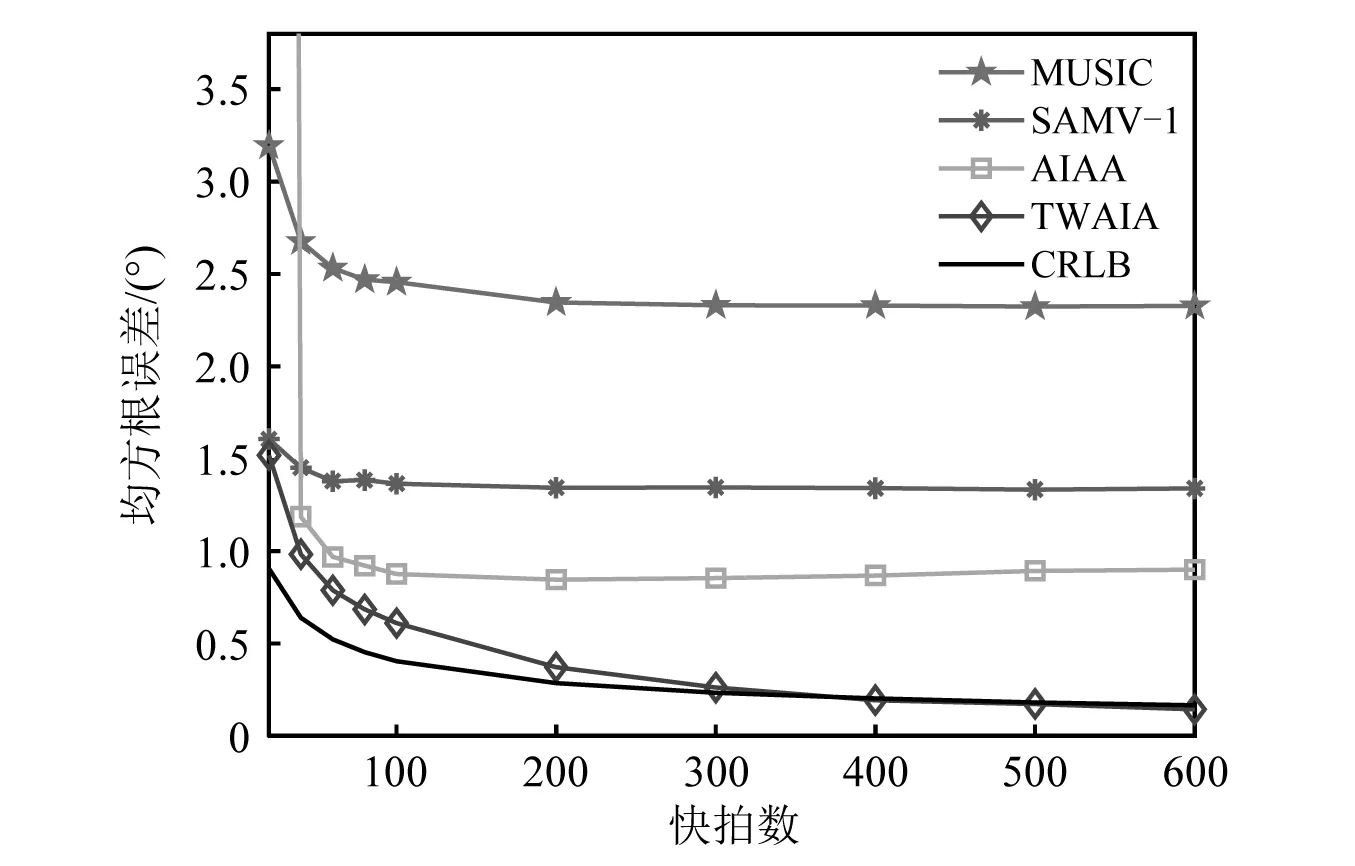
图4 均方根误差与快拍数的关系Fig.4 RMSE versus the number of snapshot

试验三：均方根误差与阵元个数的关系

图5比较了所提方法与现有方位估计方法的均方根误差与矢量传感器个数的关系，其中，信噪比为8 dB，阵元个数从2到7变化，其他仿真参数与图3保持一致。可以看到，随着阵元数的增加，MUSIC方法、SAMV-1方法、AIAA方法及所提方法的估计性能逐渐提高。MUSIC方法在阵元个数为8时无法达到无偏估计。SAMV-1方法在阵元个数为7时可实现无偏估计。AIAA方法及所提方法在阵元个数为5时即可实现无偏估计。相较于未校准的MUSIC方法和SAMV-1方法，在无偏估计性能的情况下，所提方法与AIAA方法需要的阵列孔径最小。此外，在具有相同孔径的条件下，相较于AIAA方法所提方法具有更高的估计精度，这充分展现了所提方法在小孔径时优越的方位估计性能。

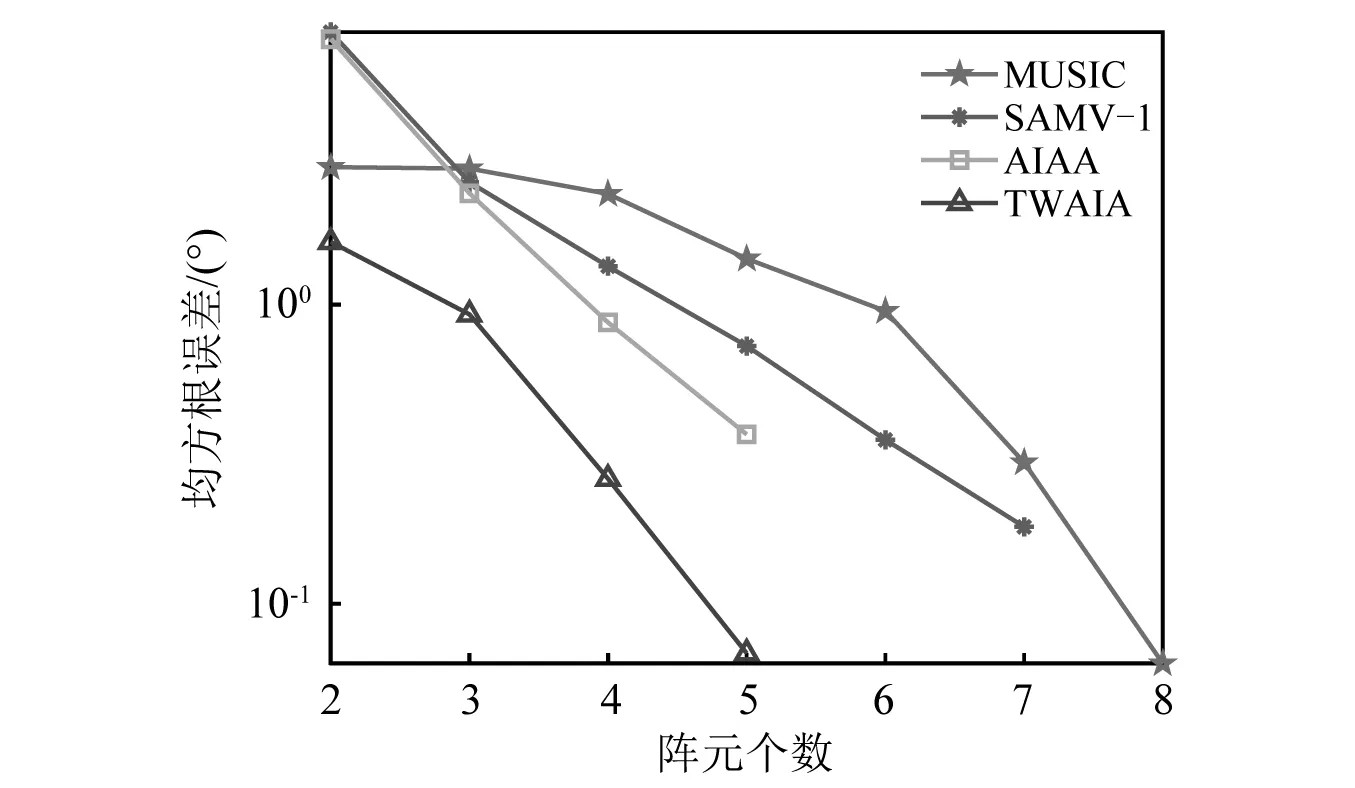
图5 均方根误差与阵元个数的关系Fig.5 RMSE versus the number of snapshot

试验四：均方根误差与偏差均值的关系

图6比较了所提方法与现有方位估计方法的均方根误差与矢量传感器阵列轴向角度偏差均值之间的关系，其中，信噪比为8 dB，β从5到35变化，其他仿真参数与图3保持一致。可以看出，几种方法的均方根误差都会随着β的增加而增加。相较于未考虑阵列轴向角度偏差参数的MUSIC方法和SAMV-1方法，AIAA方法和所提方法的均方根误差随轴向角度偏差均值增大的速率较大。尽管AIAA方法和所提方法的均方根误差随轴向角度偏差均值增大的速率较小，但是较于AIAA方法，所提方法的均方根误差更小，这展示出所提方法具有更好的方位估计性能。

图6 均方根误差与轴向角度偏差均值之间的关系Fig.6 RMSE versus the mean value of axial angle bias

4 结 论

为了提高低信噪比振速轴向不一致时矢量传感器阵列的方位估计精度，提出了一种两步加权交替迭代自适应的矢量传感器阵列方位估计方法。该方法采用正则化加权稀疏协方差矩阵拟合方法估计稀疏信号功率，通过对稀疏信号功率进行补偿提高了其在空域的稀疏性；利用加权最小二乘估计轴向角度偏差矩阵，并根据矩阵中偏差的分布特性，重构了期望的轴向角度偏差矩阵，以此交替的方式迭代更新稀疏信号功率和轴向角度偏差矩阵，使得最终估计的稀疏信号功率更加精确，从而提高了振速轴向不一致时矢量传感器阵列的方位估计精度。仿真结果表明，在低信噪比、少快拍、小孔径下，相较于MUSIC方法、SAMV-1方法和AIAA方法，所提方法提高了振速轴向不一致时矢量传感器阵列的方位估计精度。