基于EEMD的立管涡激振动响应最优降噪光滑模型参数识别研究
2022-06-29刘志慧徐兴平牛怀磊
刘志慧, 徐兴平, 牛怀磊, 王 腾
(1.中国石油大学(华东) 石油工程学院,山东 青岛 266580; 2.中国石油大学(华东) 机电工程学院,山东 青岛 266580;3.中国石油集团海洋工程(青岛)有限公司,山东 青岛 266555)
随着深海资源的开发,海洋立管作为海洋平台中生产运输的关键设备,受到众多研究者的关注。准确分析海洋立管涡激振动的特性,是设计海洋立管的依据,也是损伤分析的基础。实际监测中,真实信号受到环境的影响,产生较大的干扰易导致信号失真,因此需对测量数据降噪处理,进行信号识别。对立管涡激振动非线性信号的辨识,主要集中在利用傅里叶变换识别涡激振动频率,多数的研究手段是基于线性和平稳的假设进行的,因此有必要引入新的方法进行研究。Huang等[1]提出一种非参数的数据驱动算法,即经验模态分解(empirical mode decomposition,EMD),用来解决现实世界的非线性非平稳信号的分解和时频分析。EMD自提出后,在很多领域都得到了广泛的应用[2-5]。广大学者在研究中发现EMD方法存在一个最主要问题模态混淆现象:在同一个本征模态函数(intrinsic mode function,IMF)分量中存在不同幅值或频率的信号,或者在不同的IMF分量中存在非常相似的信号。Wu等[6]在研究白噪声信号的统计特征基础上,提出总体平均经验模态分解(ensemble empirical mode decomposition,EEMD)方法,依据数据本身的时间尺度特征进行时频分析,分解的过程保留了数据本身的特性,在处理信号的过程中能够避免傅里叶变换带来的缺陷,如出现虚假频率和多余信号分量等[7-9]。EEMD成功解决了模态混合问题,Yi等[12-13]提出置信指数算法和最大能量法选择敏感的IMF,用于研究轴承故障诊断。Prosvirin等[14]在研究滚动轴承故障诊断时将碰摩的存在度比率和基于Kullback-Leibler散度的相似性度量结合到IMF质量度量中来选择有意义的信号主模式。
EEMD虽然有效解决了模态混合问题,但在完成分解过程后生成有限的IMF集合,它的数量远远大于有实际物理意义的IMF数量。如何自适应地确定海洋立管涡激振动包含特定振动信息的具有实际物理意义的IMF成为面临的困难。因此,本文基于EEMD对海洋立管涡激振动特征进行识别,基于响应数据分解,考虑光滑度、相似度、存在度建立最优降噪光滑数学模型,以获得具有实际物理意义的有效IMF分量。
1 基于EEMD的最优降噪光滑数学模型
为获得具有实际物理意义的有效IMF分量,需要首先对立管涡激振动响应进行降噪处理,对经过EEMD分解的IMF进行信号重构,在此基础上考虑信号的相似度、光滑度和存在度,建立最优降噪光滑算法的数学模型,基于此进行有效IMF的选择。该模型由总体平均经验模态分解、重构信号、目标寻优三部分组成。
1.1 总体平均经验模态分解
总体平均经验模态分解利用白噪声频谱均匀分布的特点,对原始信号多次加入不同的高斯白噪声进行EMD分解。增加的白噪声与不同尺度的组成成分均匀地填充在整个时频空间。当信号被添加在这个均匀分布的背景中时,不同尺度的信号将自动投影到由背景中白噪声建立的参考尺度上。增加的白噪声用足够多的试验进行平均抵消,只有信号分量在总体均值中保留下来。EEMD具体步骤如下。
步骤1原始信S(t)中多次添加自适应性白噪声信号Bi(t),得到加噪信号xi(t)
xi(t)=S(t)+σiBi(t)
(1)
式中:i为添加白噪声的次数;σi为第i次添加的白噪声的标准差。
步骤2EMD分解,将多次分解的结果取平均得到IMFs
(2)
S(t)经过EEMD分解,可表示为
(3)
式中:N为添加白噪声的总次数,本研究中取100;fim,j为第i次添加白噪声后EMD分解得到的第j个固有模态函数分量;rn(t)为原始信号的趋势分量。
1.2 重构信号(滤波算法)
信号EEMD分解后,固有模态函数按频率高低排列。高频信号一般为噪声引起,频率最低的余项为趋势项,有效信号频率往往处于高频和低频之间,因此利用带通滤波的方法,同时去掉若干个高频和低频IMF分量,再以其余分量重构信号[15],得到降噪后的信号s(t),可表示为
(4)
1.3 目标寻优
考虑重构信号与原始信号的相似度、重构信号算法的光滑程度,构建最优化区间,根据存在度进行目标寻优。
1.3.1 相似度
相似度指的是滤波算法得到的重构信号和原始信号的相似程度,重构信号曲线越接近原始信号曲线,说明相似程度越高,用均方误差来表示
(5)
式中,N1为信号长度。
均方误差越小,表示重构信号曲线越接近原始信号,两个曲线的相似程度越高,较小的均方误差可以使重构信号保存原始监测信号的真实性。
1.3.2 光滑度
光滑度指的是曲线的曲折程度。曲线f(x)光滑是指其在区间[a,b]内连续,具有一阶连续导数,且切线随着切点的移动连续转动即曲率相等。
若曲线连续,则有
f(x0)=g(x0)
(6)
切线连续,则一阶导数相等
f′(x0)=g′(x0)
(7)
曲率相等,则有
(8)
将式(7)代入式(8)可得
f″(x0)=g″(x0)
(9)
将二阶导数按离散公式展开,左右两侧分别为
(10)
(11)
将式(10)和式(11)代入式(9)可得
f(x0+2h)-f(x0-2h)-2[f(x0+h)-f(x0-h)]=0(12)
因此,对于任意一条曲线,任意连接点x0处光滑度的指标可表示为
MS,f|x=x0=f(x0+2h)-f(x0-2h)-
2[f(x0+h)-f(x0-h)]
(13)
式中:h为步长;MS,f越接近于零,则曲线f(x)在除左右两个端点之外的x0邻域内越光滑。
1.3.3 存在度
基于EEMD得到的IMF建立滤波算法,考虑算法的相似度指标和光滑度指标,构造目标函数[16-17]为
{f}={λ(EMS,f)+(1-λ)(MS,f)}
(14)
式中:λ为相似度的影响因子;1-λ为光滑度影响因子。
考虑20%浮动,最优化区间下限设置为目标函数的最小值,上限设置为目标函数最小值的1.2倍,即[min{f},1.2min{f}] 。FIM,i的存在度用第i个IMF在最优化区间中所有算法中出现的频率表现,可以表示为
(15)
式中,p为IMF出现的频率。
最优化区间中,若FIM,a在所有算法中存在度最高,则判断FIM,a为有效IMF,对应仅包含FIM,a的算法为最优光滑降噪模型。
2 仿真信号验证
为证明构建的数学模型的有效性,采用仿真信号模拟的方法进行验证。
由于涡激振动信号频率交错,很难用单一的模型表示,考虑到涡激振动信号的特点(顺流向涡激振动的频率是横流向频率的二倍),采用两个周期信号与间歇信号,噪声信号相统一的复合信号模型来仿真模拟。
x(t)=s1(t)+s2(t)+c(t)+n(t)
(16)
周期性信号分别取为
s1(t)=10cos(20πt)
(17)
s2(t)=8cos(10πt+π/2)
(18)
间歇信号取为间断随机信号;噪声信号取强度为0.5高斯白噪声,各个信号及其合成信号如图1所示。
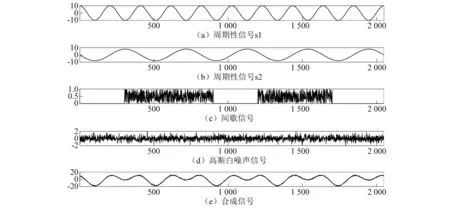
图1 涡激振动合成信号Fig.1 Composite signal of VIV
2.1 数值模拟涡激振动信号有效IMF选取
对数值模拟涡激振动信号x(t)进行总体经验模态分解,得到10个模态分量FIM,1-FIM,10和趋势项R10,如图2所示。

图2 仿真模拟信号的EEMD分解Fig.2 EEMD decomposition of simulation signals
针对10个IMF,构建28个滤波算法BP1-28,进行最优降噪光滑计算,结果如表1和图3所示。
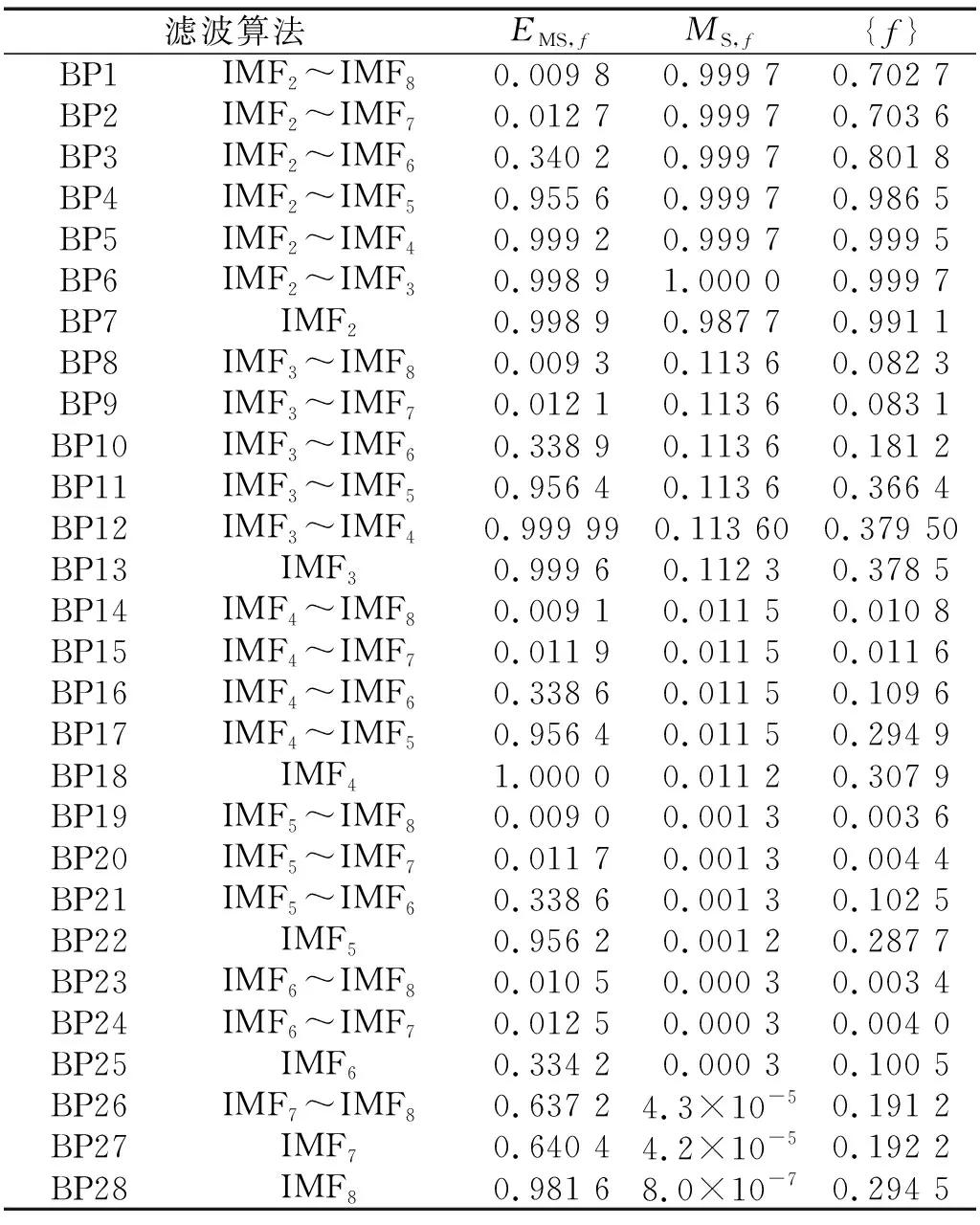
表1 滤波算法性能数据Tab.1 Performance data of filtering algorithm
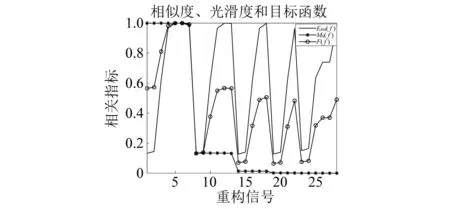
图3 滤波算法性能指标Fig.3 Performance index of filtering algorithm
考虑到信号处理工作主要是进行涡激振动正余弦信号的提取,因此相似度影响因子和光滑度影响因子都取0.5,即算法相似度和光滑度的影响相当。
由表1数据可以看出:BP14,BP15,BP19,BP20,BP23,BP24这6个滤波算法目标函数值小于0.02,其中BP14,BP15比其余滤波算法的值大一个数量级;滤波算法BP19,BP20比BP23,BP24的计算结果略大;滤波算法BP23计算结果最小,算法包含IMF6~IMF8。从图3可以看出,滤波算法BP14,BP15,BP19,BP20,BP23,BP24目标函数比其他算法要小,在0~0.05。从图4可见:在最优化区间中,IMF6和IMF7存在度最高。
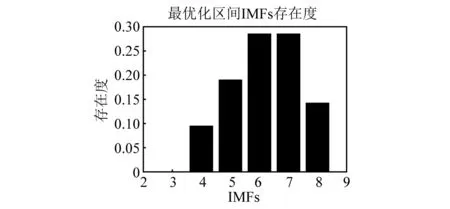
图4 最优化区间存在度Fig.4 The ratio of existence for IMFs
因此从目标函数值最小的角度考虑,建立的最优降噪光滑数学模型为算法BP23,包含IMF6~IMF8。考虑存在度,建立的最优降噪光滑数学模型为算法BP24,包含有效本征模态函数IMF6~IMF7。可见考虑存在度建立的最优数学模型不一定对应目标函数计算结果最小的算法,这是区别于一般最优降噪光滑数学模型的地方。
2.2 结果验证
为考察判断结果的准确性,从本征模态函数与原信号中周期性信号的相关度、频率比较,以及能量贡献度3个角度进行验证。
由数理统计可知,数据相关性可用相关系数表示
(19)
式中:cov(FMI,i,x)为IMF与周期性信号x的协方差;D(FMI,i)为IMF的方差;D(x)为周期性信号x的方差。
相关系数|ρf|越趋近于1,说明该IMF和信号线性相关程度越高,二者的图形越相似。IMF和信号s1,s2相关度如图5所示,相关系数见表2。
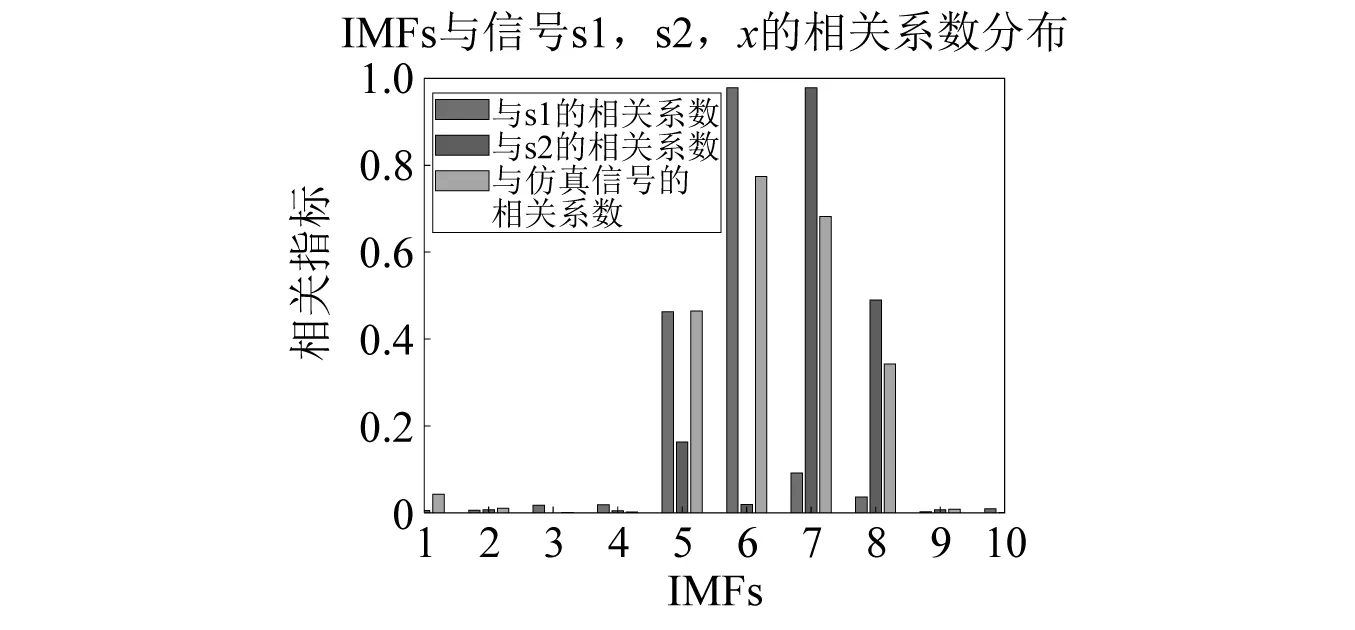
图5 IMFs和原始信号的相关度Fig.5 Correlation between IMFs & periodic signals
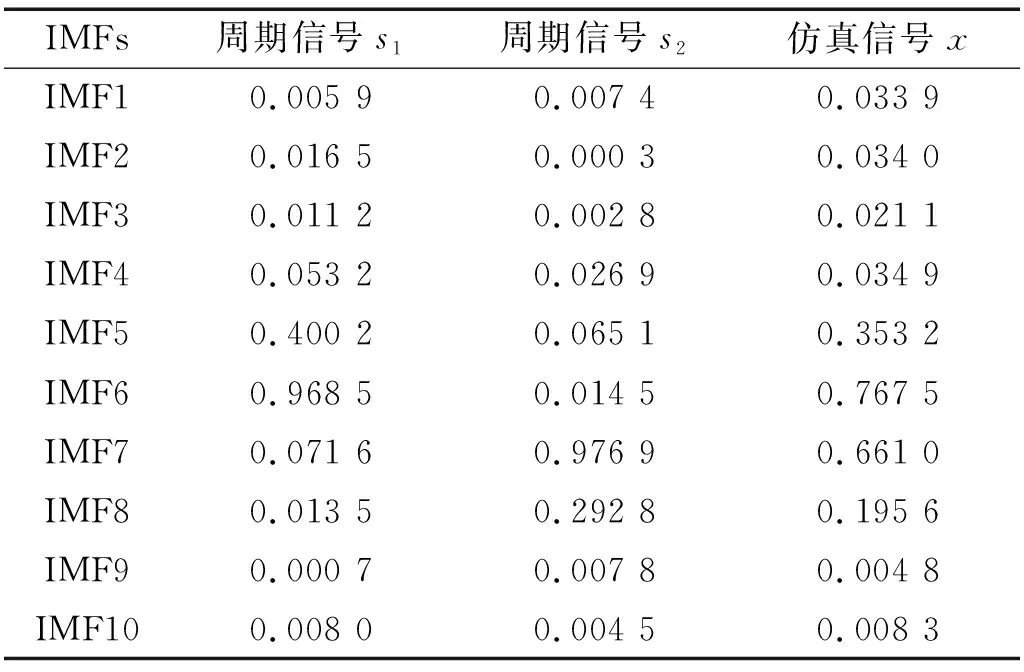
表2 IMFs与信号s1与s2、仿真信号相关度Tab.2 Correlation between IMFs and signals
由图5可以看出IMF6和周期性信号s1相关度最高,IMF7和周期性信号s2最相关。由表2可知,IMF6与s1信号相关度为0.968 5,IMF7与s2信号相关度为0.976 9,二者数值在均接近于1,因此IMF6与信号s1形状最接近;IMF7与信号s2形状最接近,且IMF6和IMF7与仿真信号的相关度均在0.6以上。
将IMF6与IMF7做频谱分析,可得IMF6的频率为10 Hz,与s1的频率一致;IMF7的频率为5 Hz,与s2的频率一致,如图6所示。这说明基于构建的最优降噪光滑模型得到的有效IMF频率与原始信号频率保持一致。
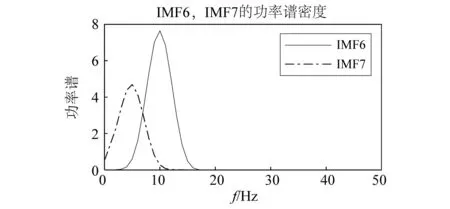
图6 IMF6与IMF7的频谱分析图Fig.6 Spectrum analysis of IMF6 and IMF7
在时域内,将本征模态函数的幅值平方对时间进行积分,可得能量谱密度,表示每个频率在整个时间长度内的能量积累[18],表达式为
(20)
根据式(20)计算IMFs能量,可以得到IMFs能量分布图谱,如图7所示。从图中可以看出,IMF6和IMF7在整个信号中占主要地位,经计算可知其能量占总能量的97.98%。
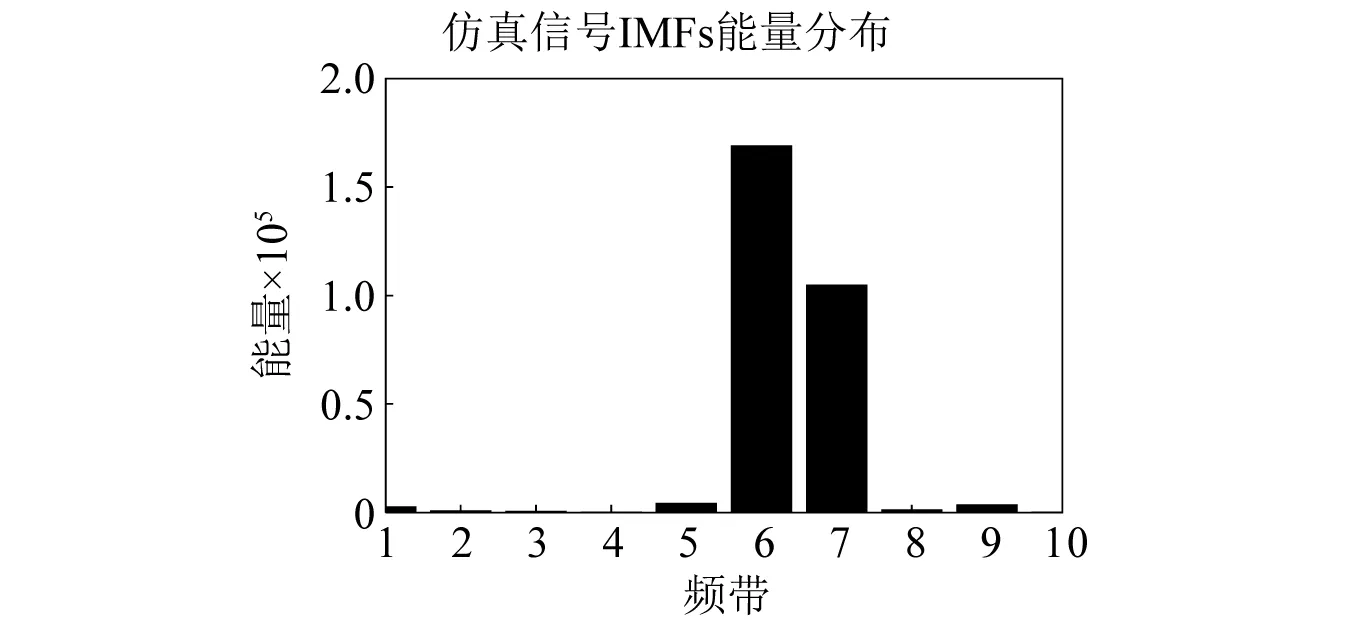
图7 IMFs能量分布Fig.7 Energy distribution of IMFs
上述从相关性分析、频谱分析、能量谱分析3个角度证明:利用本文构建的算法优选的IMF6,IMF7分别和模拟涡激振动顺流向特点的周期信号s1(t)和横流向特点的周期性信号s2(t)相关性最大,且频率对应相等,在整个信号中能量占比高达97.98%。这说明重构信号去除了仿真信号中的干扰信号,能够准确识别原始信号中的周期信号,保存了原始信号的真实性,验证了由构建的最优降噪光滑算法得到的有效本征模态函数的准确性。
3 试验数据分析
为了验证最优光滑数学模型的适用性,本文对光滑立管模型进行试验与分析。本次试验在中国石油大学(华东)波流循环水槽中进行(见图8),水槽尺度为16.0 m×0.8 m×1.4 m,最大水深1.0 m,流速0.05~0.70 m/s。

图8 试验水槽Fig.8 Laboratory flume
试验选用外径12 mm,长度为1 500 mm的有机玻璃管作为光滑立管模型,结构特征数据见表3。试验过程中水深保持 700 mm,在立管模型中部750 mm处沿顺流向和横流向分别粘贴应变片,以测量顺流向和横流向的立管响应。试验采用东华测试DH8302动态信号测试分析系统采集应变数据,采样频率设置为200 Hz。试验流速的选取参考王海青等[19]的研究结果,依据锁振区立管的约化速度为4.5~7.0,设定水槽流速为0.110~0.233 m/s,流速间隔为0.03 m/s。

表3 立管结构特征数据Tab.3 Riser structure characteristic data
以0.17 m/s流速下的试验为例,横流向和顺流向涡激振动应变响应如图9所示。
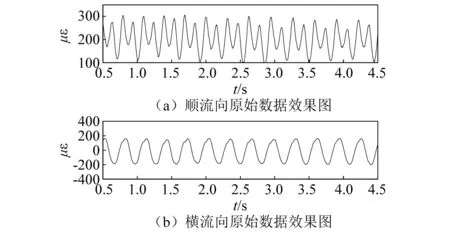
图9 涡激振动应变响应 Fig.9 Strain response of VIV
将试验测量得到的应变信号数据进行EEMD分解,得到顺流向和横流向涡激振动信号的分解结果如图10、图11所示。
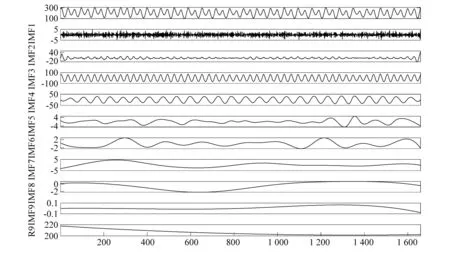
图10 顺流向信号EEMD分解Fig.10 EEMD decomposition of signals for IF
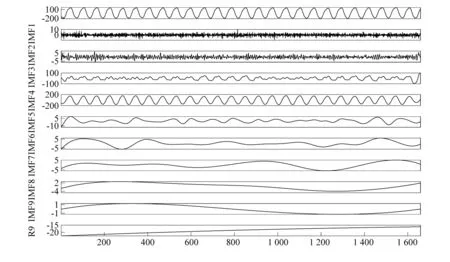
图11 横流向信号的EEMD分解Fig.11 EEMD decomposition of signals for CF
基于构建的最优降噪光滑算法,得到顺流向和横流向IMFs的存在度,如图12所示。
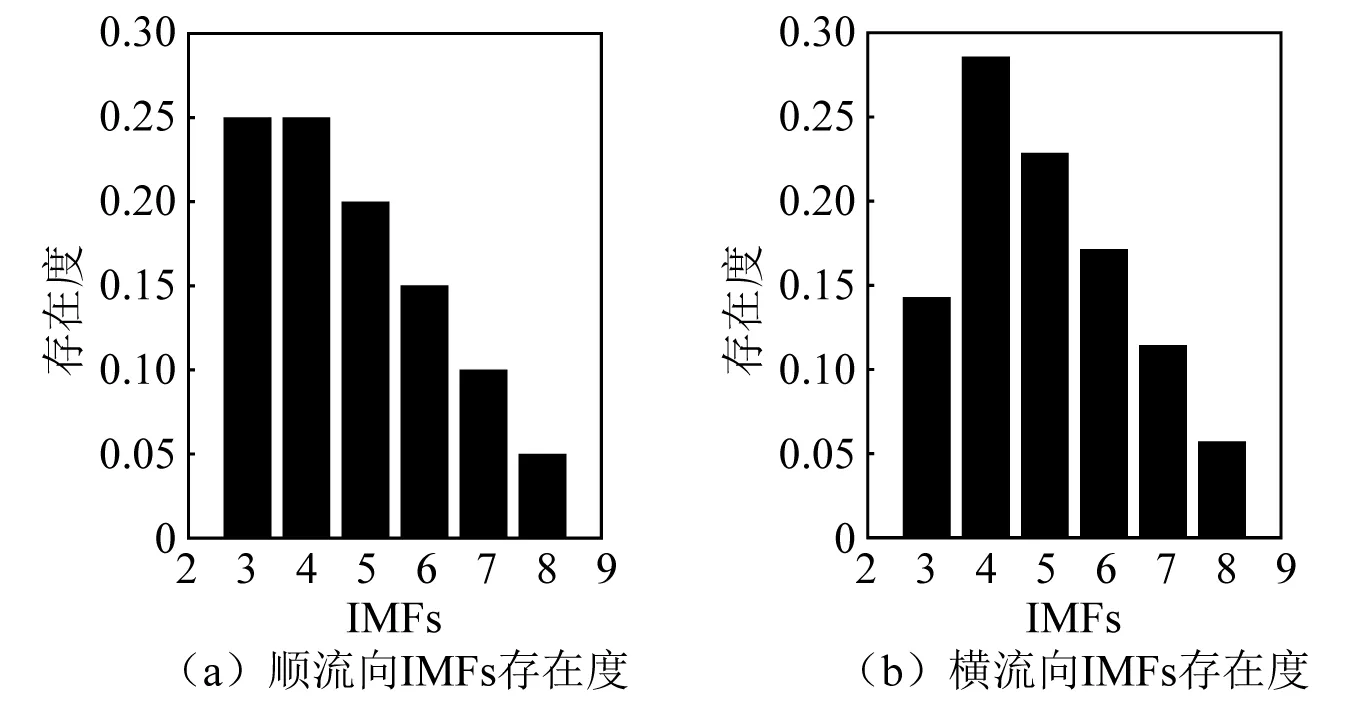
图12 涡激振动信号IMFs存在度Fig.12 The ratio of existence for IMFs in VIV
由图12可知,顺流向最优化区间IMF3和IMF4存在度最高,横流向最优化区间IMF4存在度最高。因此判断顺流向有效本征模态函数为IMF3和IMF4,横流向有效本征模态函数为IMF4。
为了判断得到的有效本征模态函数是否具有物理意义,对其进行傅里叶频谱分析,结果见图13。由频谱分析结果可得:顺流向对应的本征函数模态IMF3频率为6.25 Hz,IMF4频率为3.125 Hz,横流向对应的本征函数模态IMF4频率为3.125 Hz。
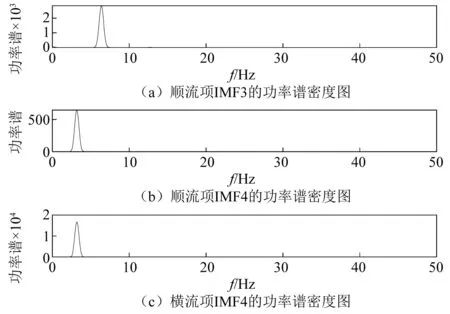
图13 涡激振动频谱图Fig.13 Spectrum of VIV
从本文结果可知,顺流向有两个频率参与到振动中去,分别是IMF3和IMF4;横流向有一个频率参与到振动中,对应IMF4。从数据关系分析可得顺流向IMF3的频率是横流向IMF4频率的2倍,这和文献[20]的研究结果(顺流向主导频率为横流向主导频率的二倍)是一致的。同时发现:顺流向有效本征模态函数IMF4的频率和横流向IMF4频率相等,这说明顺流向振动受到横流向振动的影响,这是由于漩涡脱落的过程中顺流向受到漩涡脱落垂向的分力,横流向受到漩涡脱落水平向分力的影响。
为进一步验证结果的准确性,利用IMFs能量分布进行分析,结果如图14所示。
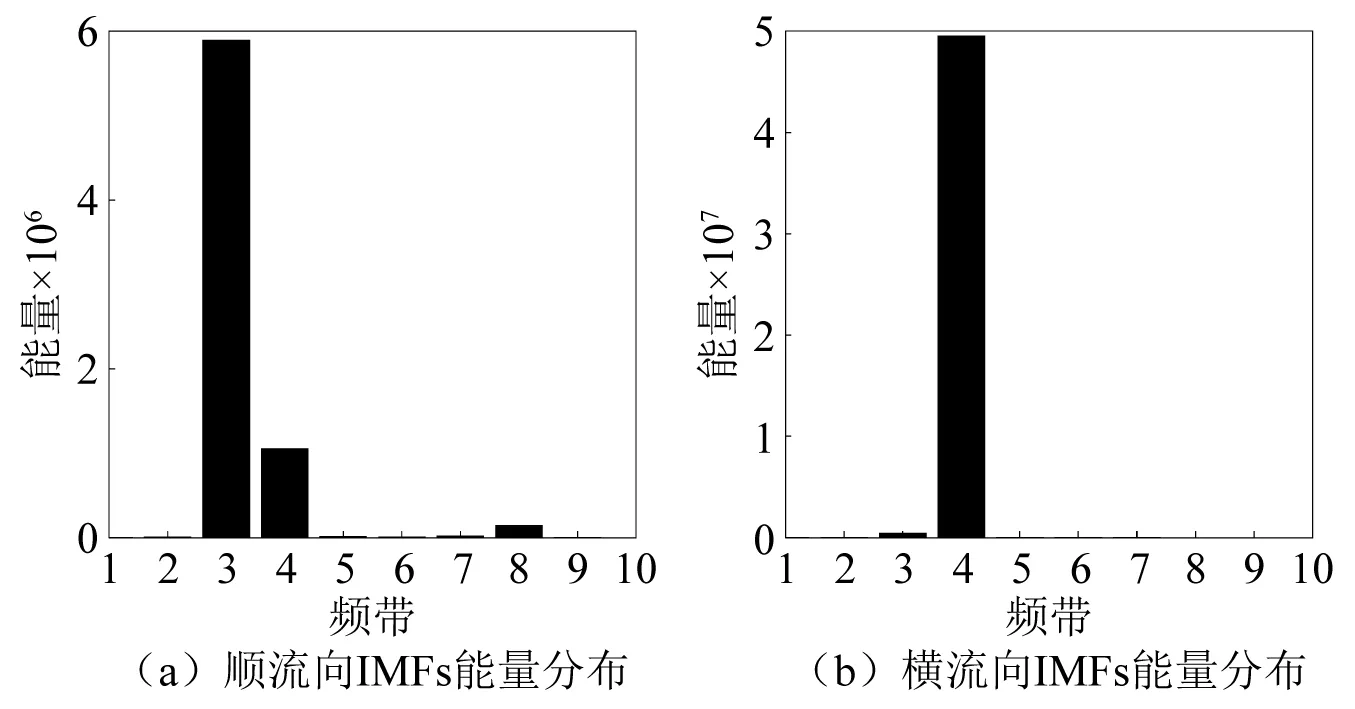
图14 IMFs能量谱Fig.14 Energy distribution of IMFs
由图14可以看出,在0.17 m/s的流速下顺流向和横流向的能量对应的频段正好是相应的有效本征模态函数对应的频段,说明本征模态函数选取是正确的。
为了验证该方法的通用性,对各工况进行了同样的分析,并将得到的有效IMFs及其能量占比汇总,如表4所示。

表4 各工况下有效IMFs能量占比Tab.4 Energy ratio of effective IMFs
从表4可以看出,在0.11~0.23 m/s的流速内,基于构造的最优降噪光滑数学模型得到的顺流向和横流向有效IMFs占总能量的95%以上,证明该方法识别有效IMFs是准确的。
4 结 论
文中采用EEMD算法对信号进行分解,基于信号曲线的相似度、光滑度、存在度构建了最优降噪光滑数学模型,进行立管涡激振动响应参数识别。结果表明:
(1)构建的最优降噪光滑数学模型可以进行有效IMF的优选和信号参数识别。
(2)仿真信号识别表明,优选的IMFs与原始信号频率成分相关系数达到0.96以上,且频率对应相等,能量占原始信号总能量的97.98%。从相关度、频谱分析、能量谱分析3个角度证明基于该算法选择有效本征模态函数的方法是准确的。
(3)涡激振动试验结果表明,经过该算法优选的IMFs能量占总能量的95%以上,顺流向有效IMFs包含2个,横流向有效IMFs包含1个,且顺流向主要频率是横流向频率的二倍关系。基于构建的数学模型选取的IMFs含有明显的涡激振动信息,这为后续涡激振动抑制、损伤分析的研究奠定了基础。
Vol.41 No.12 2022
