基于波叠加法近场声全息的一种组合型射线波函数法

陈岩豪， 石梓玉， 向 宇， 陆 静， 王玉江

(1. 广西科技大学 广西汽车零部件与整车技术重点实验室，广西 柳州 545006；2. 广西科技大学 机械与交通工程学院，广西 柳州 545006)

波叠加法(或称等效源法)自Koopmann等[1]提出以来，因其具有无网格、精度高、适用于任意形状结构等诸多优点，已被广泛应用于各种声学问题的计算中[2-6]。该方法是一种多点单极法[7-8]，其基本原理是在声源面内缩的一个封闭虚拟曲面上布置离散单极子源或偶极子源来表示声源向外辐射的声场。由于虚拟源与振动面不重合，避免了边界元法所带来的复杂插值运算和奇异积分处理。然而，波叠加法虽具有上述诸多优点，但将其应用于声全息计算时，所形成的传递矩阵通常是一个大条件数的病态矩阵，极易导致求逆过程中重建结果对输入误差的高度敏感性。

为了改善波叠加法传递矩阵的病态性，以往的方法大多侧重于优化等效源的位置。Valdivia等[6-9]从数值积分的角度对比了波叠加法和边界元法后提出等效源背离重建面越远，积分的奇异性就越弱，数值逼近的误差也越低，但过大的背离距离会加剧传递矩阵病态，严重影响重建稳定性。因此，为了同时保证计算精度和稳定性，等效源位置的选取需同时兼顾奇异性与病态性[9-11]。Bai等[12]提出了一种基于黄金分割搜索和抛物线插值的等效源位置优化算法。Gounot等[13-15]设计了一种遗传算法以搜索少量单极子等效源的最佳位置，但这种搜索算法对于大量的等效源效果并不理想。Wu等[16]提出了一种通过最小归一化速度重建误差来确定最佳等效源位置的方法，并设计了一个频率阈值准则，获得了较好的声压预测精度。Bai等在总结了等效源位置优化的相关研究后指出，等效源最佳位置的选择仍然是一个复杂的问题，因为它同时取决于频率、声源性质、倏逝波的含量、传感器和虚拟源的分布方式等。由此可见，等效源最优位置的选取至今尚无一个成熟有效的方法[17]。作者对传统波叠加法声全息技术中传递矩阵的病态性进行分析后发现，其导致病态的原因是使用了无指向性的球面形式波函数。进而，从优化波函数的角度出发，提出了一种利用指向性波函数替代传统球面波函数以改善传递矩阵病态性的射线波函数法，在提高重建稳定性方面取得了一定效果[18-19]。但是，由于该方法采用格林函数的方向导数作为射线波函数，其指向性随求导阶数离散变化，此类离散型射线波函数无法针对不同重建模型声场的特性连续调节其指向性，很难获得最佳的指向性强度，在某些情况下甚至会导致重建失败。

为了进一步提高射线波函数法的重建精度和稳定性，本文通过声场重建实例分析了格林函数导数型射线波函数法的缺陷。然后，通过射线波函数法与标准Tikhonov正则化方法的类比，提出并构造了一种可连续调节指向性强度的新型射线波函数，该函数由0阶射线波函数和带组合参数的m阶射线波函数构成，通过改变组合参数，可以连续调节波函数的指向性强度以适应不同的重建模型声场。最后，利用球面活塞声源、随机点声源以及简支板声源验证了本文提出的组合型射线波函数在声场重建中的效果。计算结果表明，组合型射线波函数可有效改善离散型射线波函数的缺陷，在两者具有同样计算精度的前提下，其传递矩阵的条件数显著降低，甚至在某些离散型射线波函数法失效的情况下，组合型射线波函数仍能保持较好的精度和稳定。

1 射线波函数波叠加法的基本原理

众所周知，基于波叠加法的近场声全息是通过测量振动体近场区域的声场信息，并求解出布置于声源内部一系列等效源的源强，进而利用这些等效源重建出声源的辐射声场。假设在全息面测量M个测点的声压，并在声源内布置N个单极子等效源，则可得到如下矩阵方程[20]

PH=GHQG

(1)

式中：PH=[p(rH1),p(rH2),…,p(rHM)]T为全息面测量得到的声压向量；GH为全息面测量声压与等效源强间的传递矩阵，其元素为自由场格林函数[GH]ij=G(rHi,rEj)；QG=[qG(rE1),qG(rE2),…,qG(rEN)]T为单极子等效源强向量。利用式(1)即可得到源强QG的反演公式

(2)

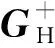
(3)

研究表明，上述传统波叠加法中的传递矩阵GH通常是一个具有大条件数的病态矩阵，因而式(2)对源强QG的求解是一个离散不适定问题。对于此类问题，如果直接求逆或使用传统的线性代数方法均难以获得稳定的源强解。为了求得有意义且稳定的源强解，必须将病态矩阵GH转化为良态矩阵，以往的方法多通过优化等效源的位置或采用正则化方法等。

向宇等的研究中对传统波叠加法传递矩阵GH的病态性进行分析后发现：由于构成该矩阵的波函数G(rH,rE)是一个仅与两点距离有关且在各个方向均以相同速率衰减的球面形式波函数，因此当全息面与等效源面相距较远或测点分布密集时，由该波函数所构成的传递矩阵GH的行向量和列向量之间将具有较强的线性相关性，并因此而导致病态。为了改善该问题，向宇等的研究中提出了一种利用指向性波函数替换球面形式波函数以提高声场重建稳定性的方法，并称之为射线波函数法。

射线波函数法的基本原理是将传统波叠加法中等效源辐射的球面波函数G(rH,rE)替换为满足Helmholtz方程和Sommerfield辐射条件且主值指向等效源对应测点的射线波函数K(rH,rE)，如图1所示。

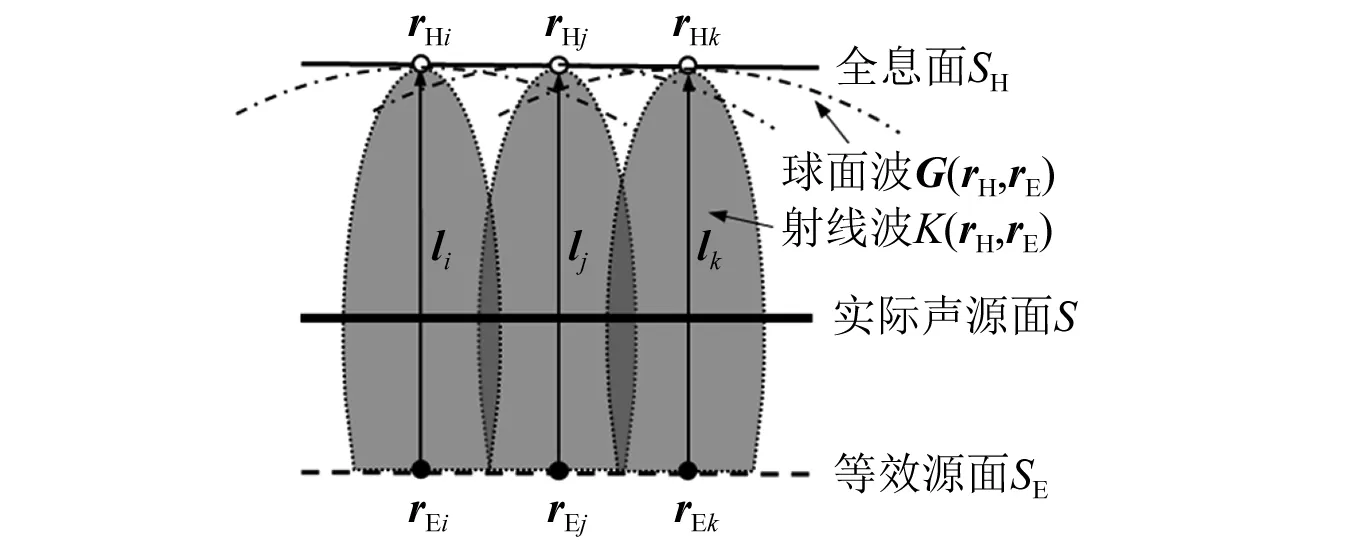
图1 等效源辐射射线波示意图Fig.1 Schematic diagram of equivalent source radiation ray wave

此时，等效源将仅在其对应测点处具有较大的声波激励(对应传递矩阵主对角元素)，而在其余测点处的声波激励则快速衰减(对应传递矩阵非对角元素)，由此即可生成一个趋于主对角占优的良态传递矩阵

KH，进而提高声场重建稳定性。

当采用射线波函数后，式(1)～式(3)重写为

PH=KHQK

(4)

(5)

(6)

式中： [KH]ij=K(rHi,rEj)为由射线波函数构成的传递矩阵；QK=[qK(rE1),qK(rE2),…,qK(rEN)]T为射线波函数所对应的等效源强向量。

2 格林函数导数型射线波函数及其缺陷

2.1 格林函数导数型射线波函数

由于满足Helmholtz方程和Sommerfield辐射条件的解析函数均可作为虚拟源的波函数，因而从理论上说，射线波函数的形式可有无穷多种。向宇等的研究中采用了格林函数G(r,rE)的方向导数作为射线波函数，记为

(7)

式中:l为求导方向；m为求导阶数。其中，求导阶数m=0即为格林函数G(r,rE)本身，称为0阶射线波函数。将求导方向l指向等效源对应测点后，所生成的传递矩阵记为

(8)

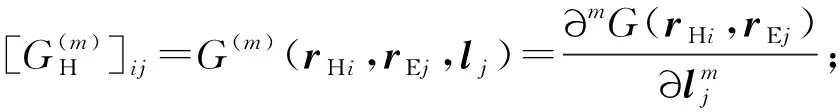
图2 0～3阶射线波函数的指向形态图(y轴方向归一化)Fig.2 Directional pattern of 0 to 3 order ray wave function

2.2 格林函数导数型射线波函数的缺陷

对格林函数导数型射线波函数的进一步研究发现，虽然求导阶数越高，射线波函数的指向性越强，传递矩阵的条件数也越低，但高阶射线波函数在重建低波数声场时误差较大。为剖析和解释该现象的原因，本文设计了一个声场重建的数值仿真。声源设置为刚性球体上的活塞声源，球体半径为a，活塞极角为θ0，如图3所示。该声源在空间场点(r,θ)处的辐射声压可用无穷级数表示为[21]

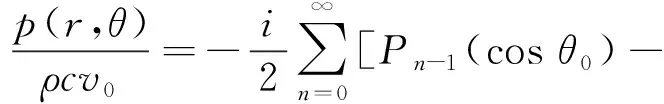
(9)

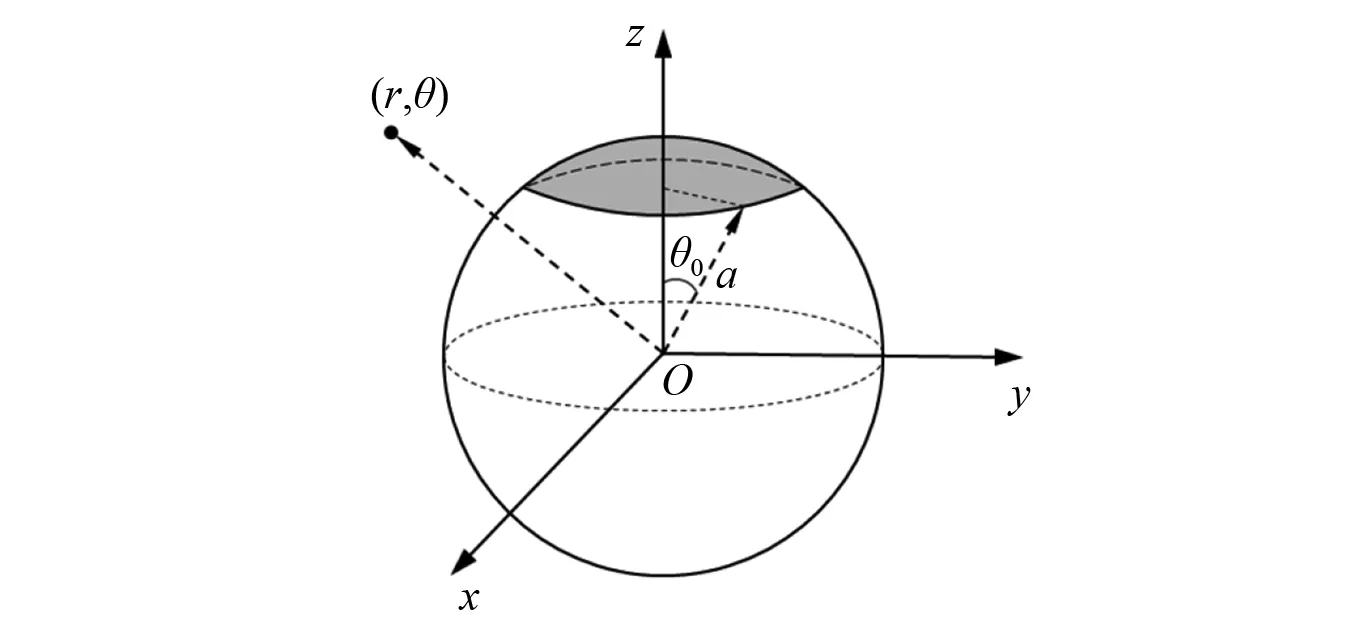
图3 刚性球面上的活塞声源Fig.3 Sound source of spherical piston

仿真中取球体半径a=1 m，活塞极角θ0=15°。全息面半径设置为1.2 m，并按纬度方向间隔2π/13、经度方向间隔π/7布置测点，测点总数为80。等效源面半径设置为0.3 m，等效源分布方式与测点相同。

由于向宇等研究的重建结果表明高阶射线波函数在k=0～2低波数内重建效果较差，在波数k>2时重建效果较好。因此，取k=1和k=5，并对比在这两个波数下，活塞声源在yz平面上的无量纲解析声压场和采用0～4阶射线波函数重建的声压场及对应的传递矩阵条件数，如图4和图5所示。

由图4可见，在k=1时，采用0～2阶射线波函数的重建声场与解析声场吻合，但传递矩阵的条件数较大，此时重建结果对输入误差的敏感程度较高；采用3阶和4阶射线波函数后，虽然大幅降低了传递矩阵条件数，理论上可以提高重建稳定性，但重建声场却与解析声场有很大的误差，并呈现出明显的放射状。而当波数k=5时，采用3阶和4阶射线波函数重建声场不仅传递矩阵的条件数远低于0～2阶，其重建结果与解析声场也吻合得较好，如图5所示。

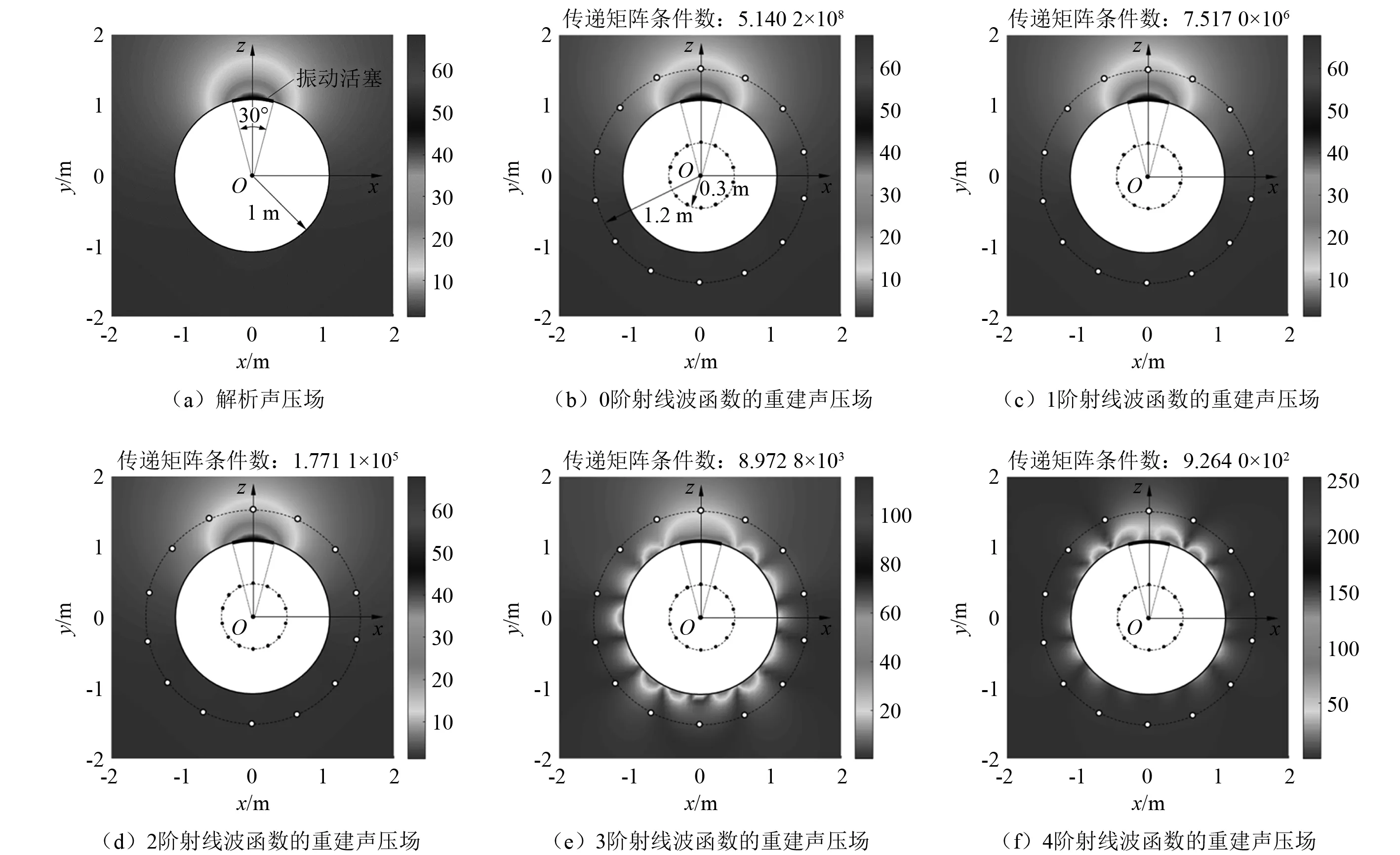
图4 当波数k=1时，球面活塞声源的无量纲解析声压与0～4阶射线波函数的重建声压Fig.4 When the wave number k=1, the dimensionless analytical sound field of the piston sound source and the reconstruction sound field of the 0-4 order ray wave function

以上两波数下的重建结果表明，高阶射线波函数重建低波数声场时的误差并非由传递矩阵的病态性引起，因为此时传递矩阵的条件数更小，自然良态性也更好。事实上，对于一个物理问题的定解，从数学上说，除需满足控制方程外，还需满足一定的边界条件。射线波函数虽然已满足控制方程(Helmholtz方程和Sommerfield辐射条件)，但由于近场声全息技术的限制，通常只能获得少量的声学测量信息作为“配点边界条件”，该配点边界条件逼近真实边界条件的程度与波函数、波数以及节点位置等均密切相关[22]。如果射线波函数的指向性太强，将导致等效源辐射的声波过于集中在主指向的射线束内，此时其重建声场除在主测点的吻合度较高之外，在其他边界点上将因波函数衰减太快而产生较大误差，无法正确的描述真实声场。这就是图4中3阶和4阶射线波函数在波数时k=1声场不吻合的原因。而当波数k=5时之所以具有较好的吻合结果，则是由于射线波函数在该波数下的指向性减弱，因此提高了配点边界条件逼近真实边界条件的精度。图6中对比了0～4阶射线波函数在波数分别为k=1(实线)和k=5(虚线)时的指向性。可以发现，在波数由k=1增加至k=5后，除0阶和1阶射线波函数的指向性无变化外，2～4阶射线波函数的指向性确实出现明显减弱。值得注意的是，虽然3阶和4阶射线波函数的指向性减弱了，但仍比0阶和1阶射线波函数的指向性更强，因而传递矩阵的条件数更低，在噪声影响下的重建效果也必然更稳定。

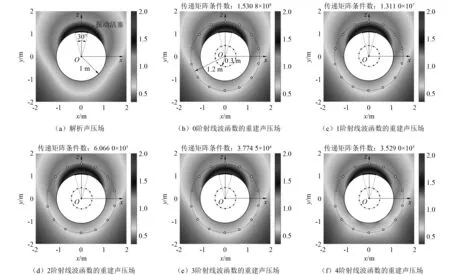
图5 当波数k=5时，球面活塞声源的无量纲解析声压与0～4阶射线波函数的重建声压Fig.5 When the wave number k=5, the dimensionless analytical sound pressure of spherical piston sound source and reconstruction sound pressure of 0-4 order ray wave function

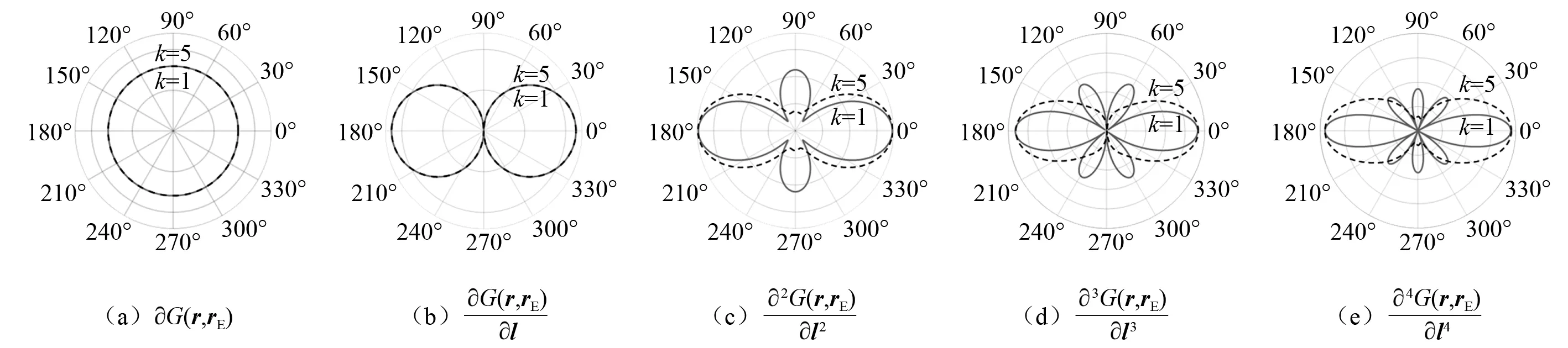
图6 波数分别为k=1和k=5时，0～4阶射线波函数的指向性对比Fig.6 When the wave number is k=1 and k=5 respectively the directivity comparison of 0-4 order ray wave functionss

综合上述分析可知，在射线波函数法中，声场重建的稳定性和精度与射线波函数的指向性强度息息相关。虽然射线波函数的指向性越强，传递矩阵越趋于主对角占优，其条件数也越低，但如果波函数的指向性过强，等效源所辐射的声场将过于集中在主指向附近，导致重建声场精度降低。反之，如果射线波函数的指向性太弱，那么传递矩阵将具有较大的条件数，导致重建声场的重建稳定性较差。

实际上，射线波函数的上述特性与正则化方法非常相似，下文将通过射线波函数与标准Tikhonov正则化方法的类比来说明其指向性在声全息计算中对精度和稳定性的影响。

Tikhonov正则化方法所获得的源强向量正则化解为[23]

(10)

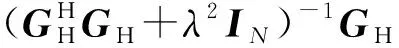
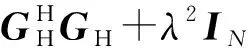
3 组合型射线波函数的构造及参数选择

3.1 组合型射线波函数的构造

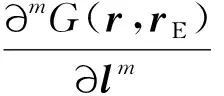
(11)

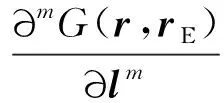
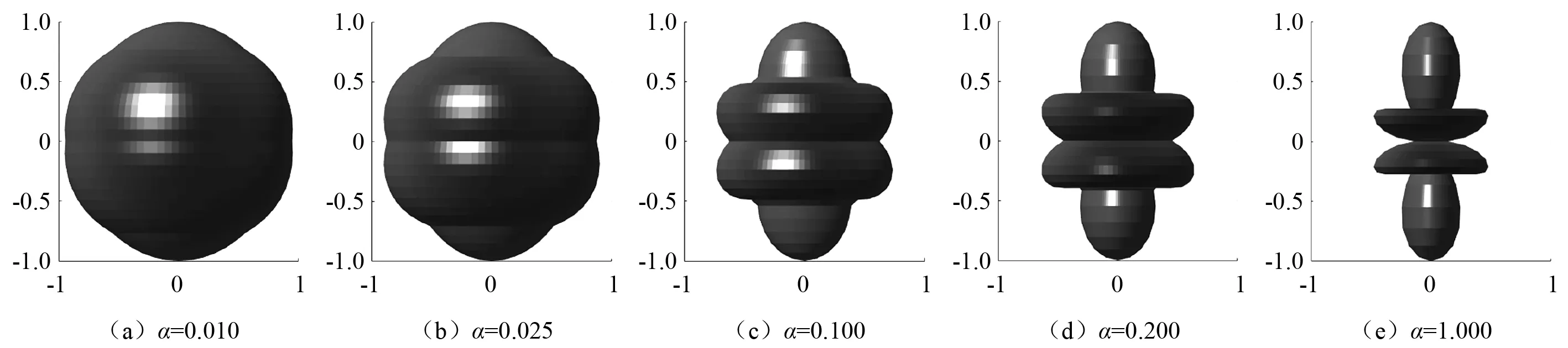
图7 组合型射线波函数随组合参数α增大时的指向性变化Fig.7 Directivity variation of combined ray wave function with increasing combination parameters α

3.2 组合型射线波函数的参数选择

实际重建过程中，声场信息通常是未知的，可结合辅助点法[24]和在波叠加法中已被广泛应用的遗传算法[25-26]选择权重系数α。在本文中的具体实施步骤为：首先在声源面与全息测量面之间设置若干辅助点，然后将参数α的选取范围设为[0， 100]并映射到一个长度为20的二进制的集合；为了保证收敛速度，选取40个参数α编码成染色体作为第一代种群，然后以辅助测点上的实际测量值p与重建值pα之间的相对误差最小作为目标函数对种群中的染色体进行筛选，即

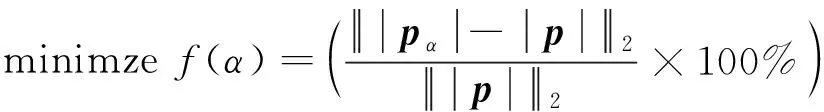
(12)

相对误差较小的染色体α，其在下一代出现的概率较大，将下一代出现的概率定义为适应度函数如下

(13)

采用轮盘赌(即每一个体被选择概率正比于其适应度函数值)在第一代种群中重复选取得到40个新的染色体。为了避免参数选取陷入局部最优，对选取的40个染色体按照一定的概率pc交换其部分基因编码区间，同时随机选取染色体的个别基因进行变异。将经过交叉和变异后的染色体作为下一代种群，再次计算适应度函数进行筛选，反复迭代，当到达其终止条件时，算法终止。

4 数值算例

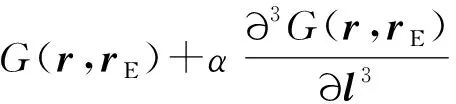
经过大量计算验证，在选定以上交叉概率和变异概率的情况下，经过30～40次迭代计算后，辅助点重建误差及组合参数变化已经基本趋于稳定，因此文中将算法终止条件设定为50次迭代。

4.1 刚性球面活塞声源的重建效果对比

由图8(a)可见，随着遗传算法迭代次数的增加，辅助测点的重建误差逐渐减小，直至趋近于0。与之相应的组合参数α也呈下降趋势，如图8(b)所示。这表明对于该重建模型，波函数的组合参数α越小，重建的数值精度越高。但是，在选择α时还必须考虑重建过程的稳定性。因为α决定了组合型射线波函数的整体指向性，若α过小，将可能导致传递矩阵由于指向性太弱而病态。例如，如果选择迭代次数为50时对应的α，虽然重建精度较高，但其传递矩阵的条件数很大，如图8(c)所示。因而，在选择α时，最好在保证精度满足需求的前提下尽量选取条件数较小时所对应的组合参数。

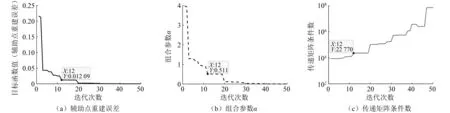
图8 遗传算法迭代过程Fig.8 Iterative process of genetic algorithm

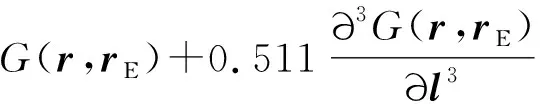
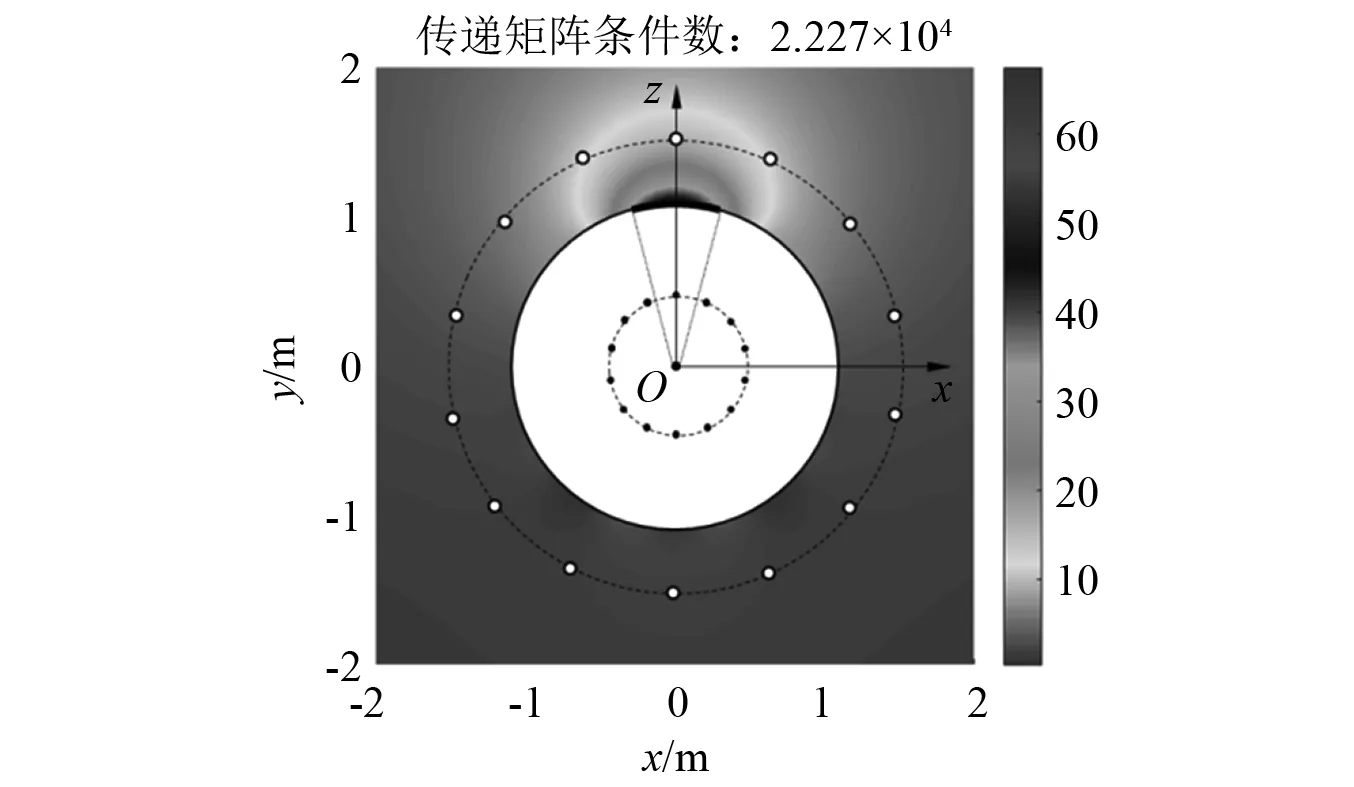
图9 组合型射线波函数的重建无量纲声压Fig.9 Reconstruction of dimensionless sound pressure based on combined ray wave function

4.2 随机分布点声源的重建效果对比

在实际工程中，由于声源形状、结构和材料的复杂性，其振动产生的声场通常较为复杂且无解析解可循。因此，利用“替代法[27]”模拟实际声源的声场。该声场由100个单极子点声源产生，这些点源随机分布于以原点为中心，大小为1 m×1 m×1 m的正方体区域内，它们在空间r处的辐射声压可由式(14)计算

(14)

式中，σi为第i个点源的强度系数，其大小从0～10中随机选取。

全息面设置为椭球面，z方向的长半轴为1 m，x和y方向的两个短半轴均为0.8 m，并按纬度间隔为π/11，经度间隔为2π/11布置测点，测点数量共100个。等效虚拟源点布置在半径为0.07 m球面上，分布间隔和数目与全息测点相同。重建面设置为高度位于z=0.65 m，边长1 m的正方形面，并以10×10的方式均匀布置100个重建节点。为了进一步考察组合型射线波函数在低波数处的重建效果，该算例中选择重建波数为k=0.2。

首先在重建面和全息面间设置20个辅助测点，并利用遗传算法搜索组合参数α。辅助点的重建误差随迭代次数的下降过程如图10(a)所示，与之相对应的组合参数α和传递矩阵的条件数如图10(b)和图10(c)所示。由于遗传算法在前几次迭代后就已经搜索出了较优的组合参数α，因而图10中3个子图的曲线在整个迭代过程的相对变化都不大。辅助测点的重建误差保持在1×10-3量级，组合参数α稳定在95～100，传递矩阵条件数稳定在1×1012量级。在该算例中我们选取了迭代到第20次时获得的组合参数α=96。

图10 遗传算法迭代过程Fig.10 Iterative process of genetic algorithm

为了更为深入和详细的讨论，分别在无噪声和信噪比为40 dB的高斯白噪声下，采用0～4阶射线波函数和组合型射线波函数计算重建面上100个节点的声压幅值，并与解析声压幅值对比，如图11所示。波函数相应的传递矩阵条件数见表1。由图11(a)和图11(b)可以看到，无论是在无噪声还是有噪声情况下，0阶和1阶射线波函数的重建误差均很大。无噪声时重建误差较大的原因在于0阶和1阶射线波函数的指向性太弱，导致传递矩阵严重病态，放大了输入数据的数值误差。显然，在添加噪声之后，其重建结果的误差必然更大。由图11(c)可以看到，2阶射线波函数在无噪声情况下的重建结果与解析解基本吻合，但在添加噪声后出现了较大误差。这说明2阶射线波函数的指向性强度大于0阶和1阶射线波函数，可以改善传递矩阵的病态，进而提高计算的精度。但是，其指向性强度仍然不足，传递矩阵仍存在一定的病态，因此在添加噪声后其稳定性下降，即欠正则化。由图11(d)和11(e)可以看到，在无噪声的情况下，3阶和4阶射线波函数的重建误差与解析解有较大误差，在添加了噪声后，重建结果几乎无变化。这说明3阶和4阶射线波函数由于指向性过强，已无法正确重建声场，即过正则化。但是，添加噪声后的重建结果与无噪声时的结果相差并不大，这又说明此时重建过程是稳定的。以上结果表明，对于该重建模型，无论采用哪一阶射线波函数，都无法同时保证计算精度及重建稳定性，即离散型射线波函数失效。当采用组合型射线波函数后，无噪声和有噪声情况下的重建结果均与解析解吻合，如图11(f)所示。由表1的传递矩阵条件数还可以发现，组合型射线波函数的条件数远远低于离散型波函数中的0阶和1阶波函数，并且与3阶波函数几乎一致，表明组合型射线波函数能有效改善离散型射线波函数的缺陷，可以同时保证计算精度和重建稳定性。

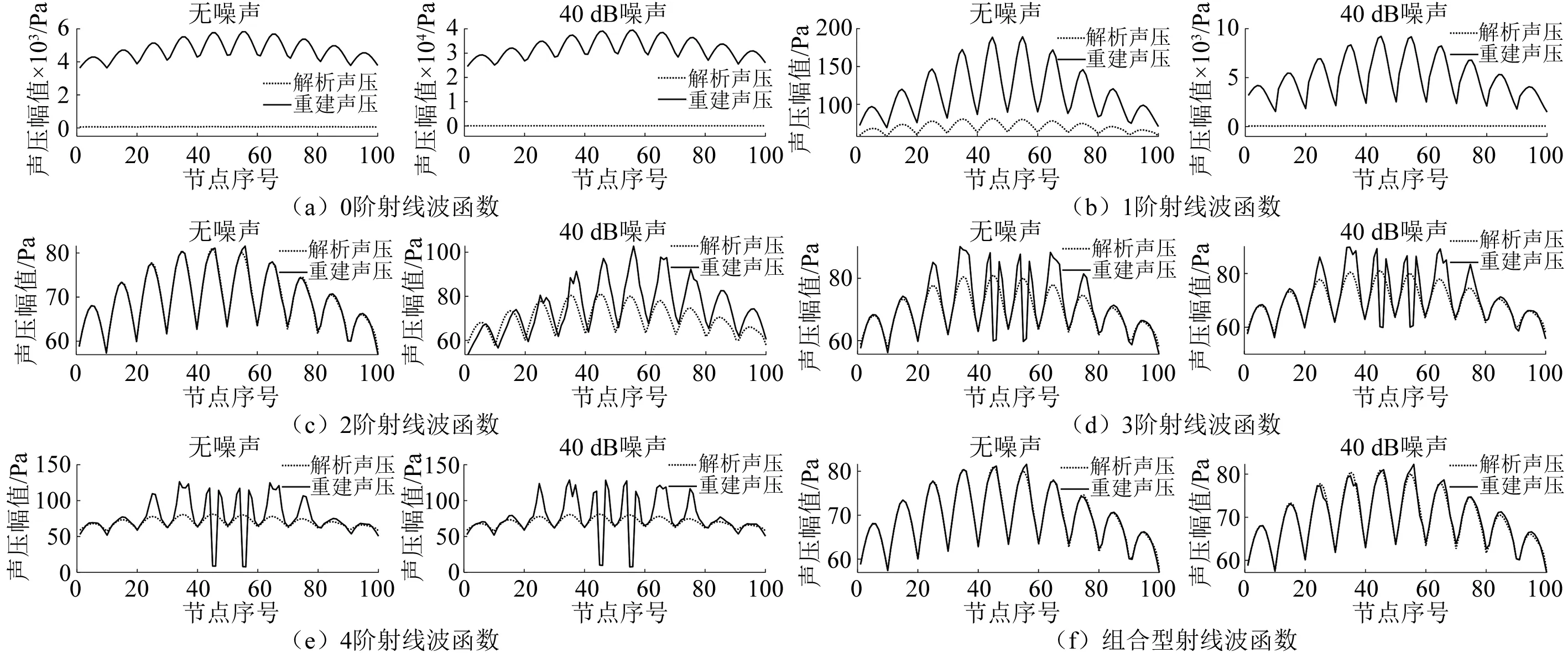
图11 0～4阶射线波函数和组合型射线波函数在无噪声和40 dB高斯白噪声下的重建声压和解析声压对比Fig.11 Comparison of reconstructed sound pressure and analytical sound pressure of 0-4 order ray wave function and combined ray wave function under no noise and 40 dB white Gaussian noise respectively

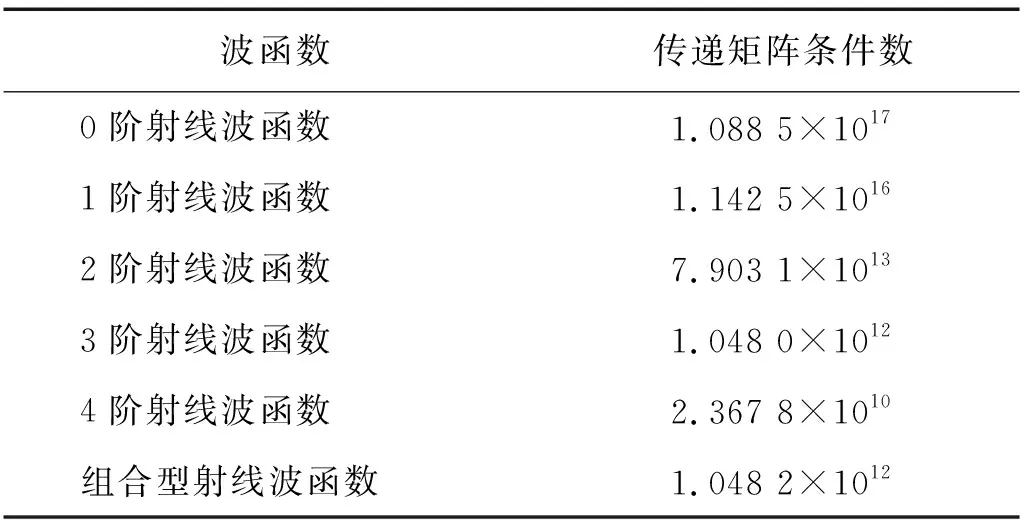
表1 0～4阶射线波函数和组合型射线波函数的传递矩阵条件数Tab.1 Condition number of transfer matrix for 0-4 order ray wave function and combined ray wave function

4.3 简支板辐射声场的重建效果对比

在实际应用中，连续分布的结构振动声源(例如板、壳等)较为常见。因此，本文采用简支板声源算例进一步验证组合型射线波函数的有效性。已知四边为无限大障板的简支板振速分布[28]为

(15)

第(m,n)阶模态振型

第(m,n)阶模态频率为

式中： 以简支板左下角为原点，在(x0,y0)处施加角频率为ω； 幅值为F的激励力时，简支板(x,y)处的振速为v(x,y,ω)；a，b和h分别为简支板的长度、宽度和厚度；E为杨氏模量；υ为泊松比；ρ1为简支板材料的密度。

根据Rayleigh积分公式可进一步得到简支板在空间r处的辐射声压[29]

(16)

式中：S为板的面积；G(r,r′)为格林函数； 空气密度ρ2=1.23 kg/m3；r′为板上任意一点。

该仿真中，设置简支板为一长宽尺寸为1 m×1 m，厚度为0.005 m的铝板，杨氏模量E= 7×1010Pa，泊松比υ=0.3，密度为ρ1=2.7×103kg/m3。全息面的大小与简支板相同并位于其正上方0.2 m处，全息面上均匀分布25×25个测点。等效源面位于简支板正下方0.1 m处，等效源分布方式与测点相同。在简支板中心施加幅值为100 N，频率为500 Hz的简谐激励力。仿真中对全息面测量声压添加信噪比为30 dB的高斯白噪声，然后分别采用0阶射线波函数、3阶射线波函数和组合型射线波函数重建简支板上方0.15 m平面处的声场，并与简支板辐射的解析声场进行对比。其中，用于搜索组合参数α的辅助测点设置为16个，均匀分布在简支板正上方0.18 m处1 m×1 m的平面上。经过搜索后得到的组合参数为α=10.25。

为了量化各个波函数的重建精度，定义重建误差为

(17)

式中，P与P′分别为重建面上的解析声压向量和重建声压向量。

简支板的解析声压与重建声压如图12所示。结合表2发现，由于0阶射线波函数构成的传递矩阵条件数较大，在信噪比为30 dB高斯白噪声的干扰下，重建声压与解析声压偏离较大，相对误差为17.14%。而3阶射线波函数和组合型射线波函数由于降低了传递矩阵的条件数，因而具有更高的重建稳定性，较好的还原了声场分布特征。进一步对比两者的重建误差可以发现，尽管组合型射线波函数的传递矩阵条件数略高于3阶射线波函数，但其重建声压相对误差仅为3.08%，低于3阶射线波函数的4.53%。为进一步考察简支板受偏心激励时本文方法的声场重建效果，将激励点位置设在(0.8，0.8)处，重建结果如图13所示。可以发现，此时组合型射线波函数依然获得了较好的重建结果，其相对误差为4.15%。

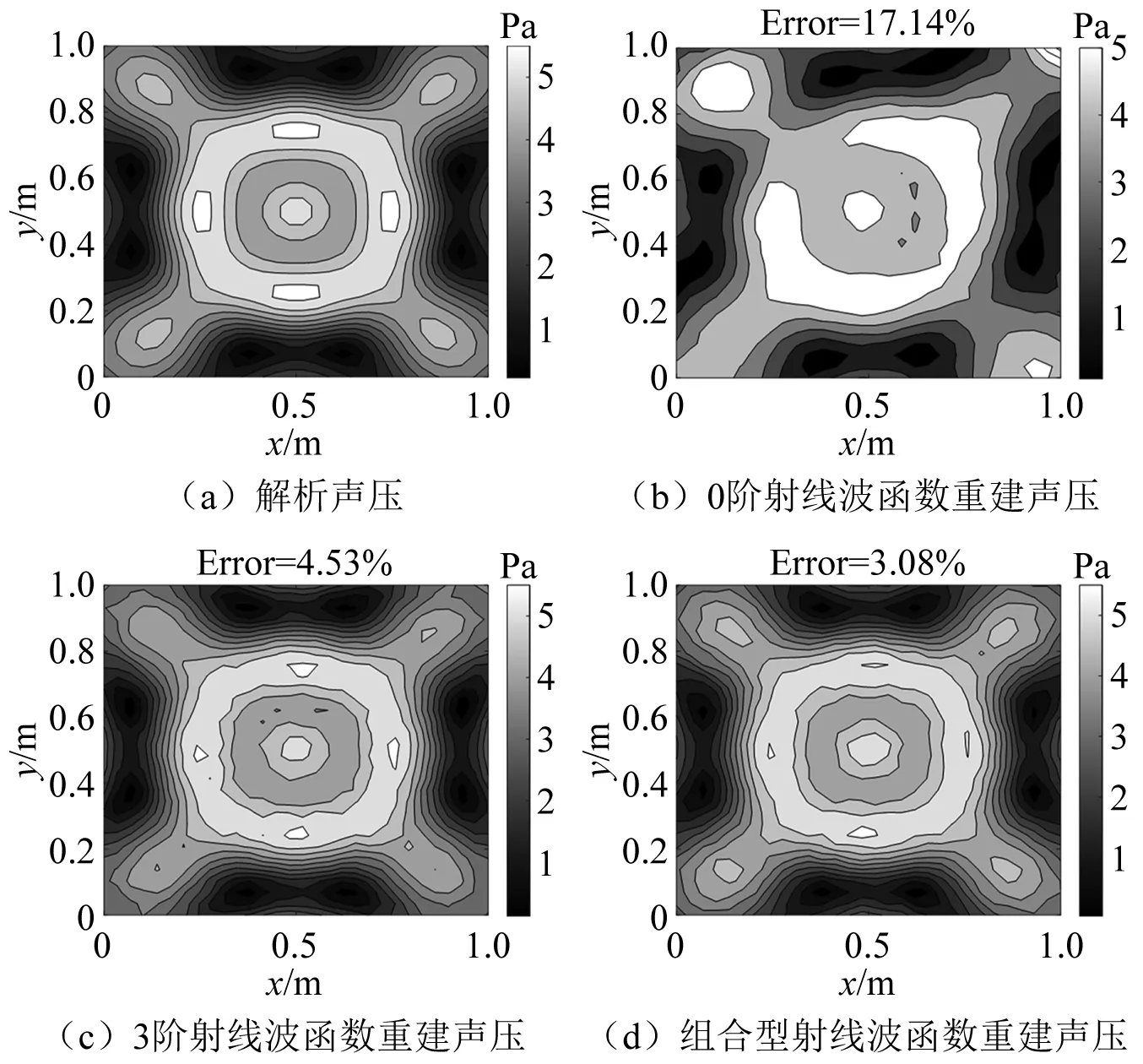
图12 中心激励简支板的解析声压及0，3阶射线波函数和组合型射线波函数的重建声压Fig.12 Analytical sound pressure of a simply supported plate under central excitation and reconstruction sound pressure of 0,3 order ray wave function and combined ray wave function

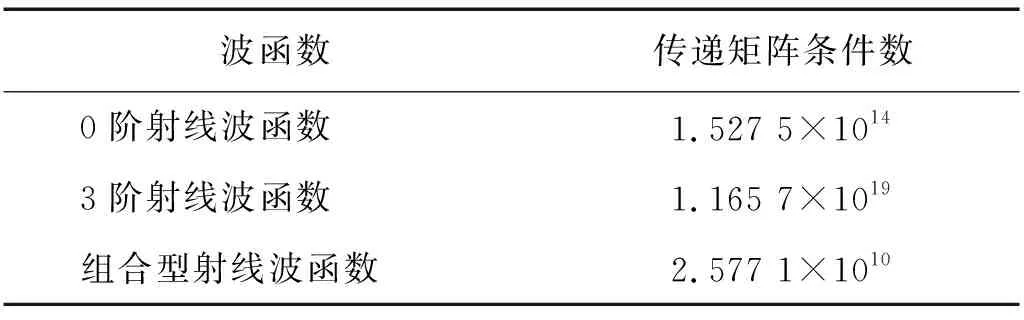
表2 0阶射线波函数、3阶射线波函数和组合型射线波函数的传递矩阵条件数Tab.2 Condition number of transfer matrix for 0, 3 order ray wave function and combined ray wave function

由此可见，即便是重建空间连续型的简支板声源，组合型射线波函数仍具有更高的计算精度和稳定性。

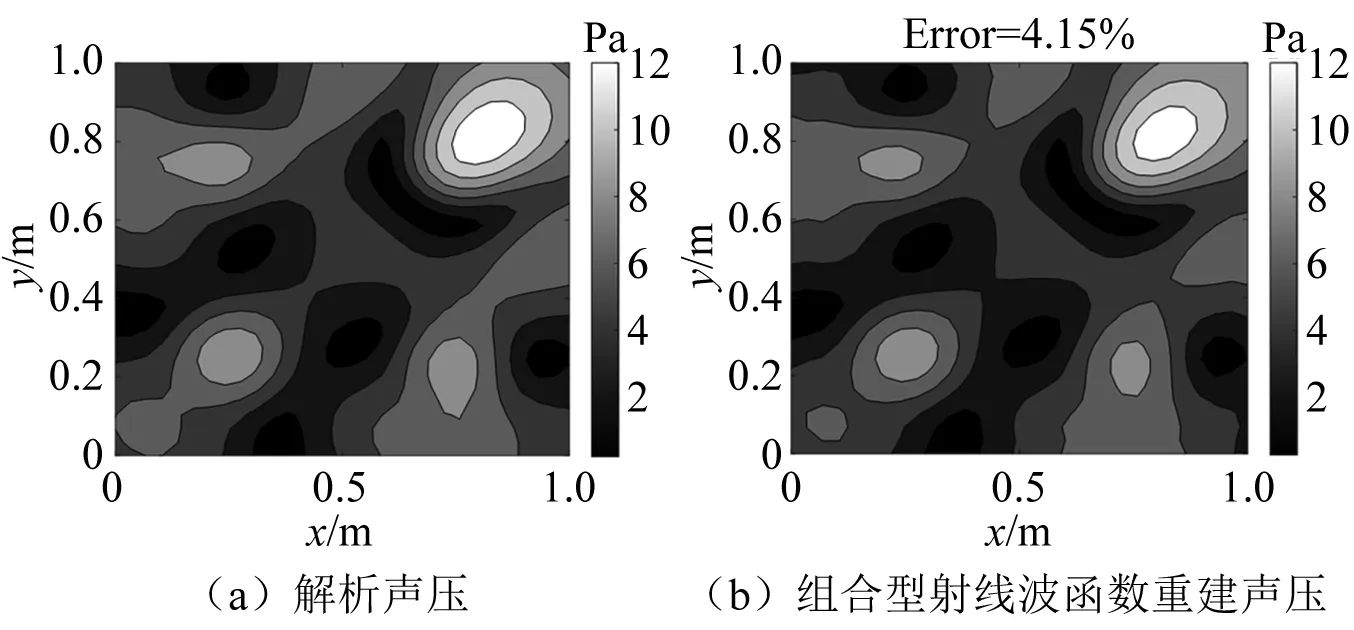
图13 偏心激励的简支板解析声压及组合型射线波函数的重建声压Fig.13 Analytical sound pressure of a simply supported plate under eccentric excitation and reconstruction sound pressure of combined ray wave function

5 结 论

针对传统波叠加法近场声全息的病态性，本文在向宇等提出的格林函数导数型射线波函数法的基础上，通过将0阶和带组合参数α的m阶射线波函数进行组合，构造了一种可连续调节指向性强度的组合型射线波函数，并结合辅助测点法和遗传算法提出了一种选择组合参数α的优化算法，可根据重建模型的特点构造具有合适指向性强度的射线波函数。利用球面活塞声源、随机点声源以及简支板声源验证了本文提出的组合型射线波函数在声场重建中的效果，并与格林函数导数型射线波函数法的计算结果进行了比较。计算结果表明，组合型射线波函数可有效改善离散型射线波函数的缺陷，并在同样保证计算精度的前提下，显著降低传递矩阵的条件数。而且，即使在离散型射线波函数法失效的情况下，本文方法仍能保证重建精度和稳定性。