大比例尺剪力墙住宅楼抗震性能振动台试验研究

高华国， 张令心， 李 行， 朱柏洁， 李 锐

(1. 中国地震局 工程力学研究所，哈尔滨 150080；2. 中国地震局 地震工程与工程振动重点实验室，哈尔滨 150080； 3. 辽宁科技大学 土木工程学院，辽宁 鞍山 114051)

近年来，随着我国城市化进程加速发展，城市人口急剧增加，20～30层的剪力墙住宅楼在大、中型城市占据很大比例。研究者对地处重要城市的住宅建筑地震破坏机理研究非常重视，聂建国[1]认为应该重视和完善结构整体抗震性能的研究，开展结构体系振动台试验是研究结构体系动力特性、破坏机理、震害原因的重要手段之一，可以为开展静力试验提供理论依据。程绍革[2]进行1/20模型试验，弹性阶段吻合良好，低楼层外围墙肢出现水平裂纹，在模拟大震试验阶段，底部外围墙肢水平裂缝贯通。郭宏超等[3]针对西安火车站东配楼复杂连体结构开展了振动台试验，得出结构在9度罕遇地震下刚度退化率达到23.73%，与数值模拟进行了对比，得出振动台可以有效的对复杂结构进行分析。文献[4-5]在剪力墙结构体系振动台试验中，出现外围墙体出现水平裂缝，指出体系扭转效应在结构设计中不能忽略。比例尺过小导致模型轴压比与原模型轴压比的比例失真，墙肢破坏表现出小轴压比的破坏现象，不能很好的体现出罕遇地震下结构的真实破坏机理。文献[6]试验结果表明，剪力墙结构破坏主要发生在与墙肢相连的连梁端部，连梁是短肢剪力墙的薄弱环节。规程对于剪力墙结构关于楼层最大层间位移与层高之比的限值对于短肢剪力墙结构来说过于严格。短肢剪力墙墙体纵筋配筋率不宜小于1.2%，其他部位不宜小于1.0%的规定过于保守，结构刚度偏大，规范对短肢剪力墙的布置、抗震等级及其轴压比限值等给出了比普通剪力墙更为严格的限制，而对短肢剪力墙的计算模型、适用高度和构造措施等均未明确说明。王威等[7]对双向加载下波形钢板剪力墙抗震性能进行研究，提出双向加载下的钢板剪力墙面内抗震性能出现不可忽视的削弱，并且滞回曲线出现明显的捏拢现象，认为双向地震作用对构件的削弱不可忽视，建议适当增加安全系数。Martinelli等[8]对7层足尺剪力墙结构振动台试验模型进行非线性动力分析，分析结果与试验吻合良好，受试验条件限制，足尺试验模型只能取出简单结构进行试验和计算，不具备普遍性。因此，有必要开展大比例尺、全人工质量的剪力墙结构体系模型试验。

我国近期大型地震主要发生在剪力墙结构分布较少的地区，剪力墙震害现象较少，2010年2月27日发生在南美洲智利的8.8级地震中，高层剪力墙结构破坏比较严重，文献[9-13]中震害表明，不合理的边缘构件设置、轴压比过大、构造要求不合理等是造成高层剪力墙结构体系破坏的直接原因，规范滞后成为居住要求提高的主要瓶颈，也是地震震害产生的根本原因。文献[14]提及到的位于智利的Concepción市15层Alto Río剪力墙居民楼整体倒塌，主要可能破坏原因是受力钢筋屈服、箍筋屈服、受压区混凝土破坏、墙体剪切破坏。高层倒塌会导致大量人员伤亡和巨大经济损失，开展大比例尺振动台实际模型试验研究大震下剪力墙抗震结构体系的破坏机制成为目前迫切需要解决的问题，基于此笔者以某高层住宅楼为原型，以1/8大比例尺为几何相似关键参数，开展震动台试验，研究结构损伤及地震响应，为该类建筑的施工与设计、加固与改造提供一定的技术支持。

1 振动台试验设计

1.1 模型设计

试验在中国地震局地震工程与工程振动重点实验室进行，模型取自课题组在某地区抗震普查中比较典型的住宅楼为试验体，共15层，采用剪力墙结构，抗震设防烈度为7度，地震分组一组，场地类别为Ⅱ类，层高2.9 m，总高度为43.5 m，剪力墙厚度为200 mm，受力钢筋采用RRB400，箍筋采用HPB300，墙体混凝土采用C30，1～3层连梁截面尺寸为200×500，4～15层尺寸为200×400，板厚为120。连梁、板混凝土采用C30。基本风压0.35 kN/m2，基本雪压0.55 kN/m2，活载为0.2 kN/m2，短肢剪力墙结构按照2010版以后相关设计规范设计。模型采用配合比为：1∶3.2∶0.6的砂浆，经过实验室测试7 d，14 d，28 d强度，考虑施工、制作等因素，选定M7.5的砂浆作为最终的模型用材料。受力筋采用镀锌铁丝Φ2.5，Φ1.6，分布钢筋及箍筋采用配点焊铁丝网，根据试验条件，采用全人工质量配重，配置人工质量14 t，结构体系以剪力墙为为主，构件布置图如图1所示，模型施工、竣工图如图2所示。

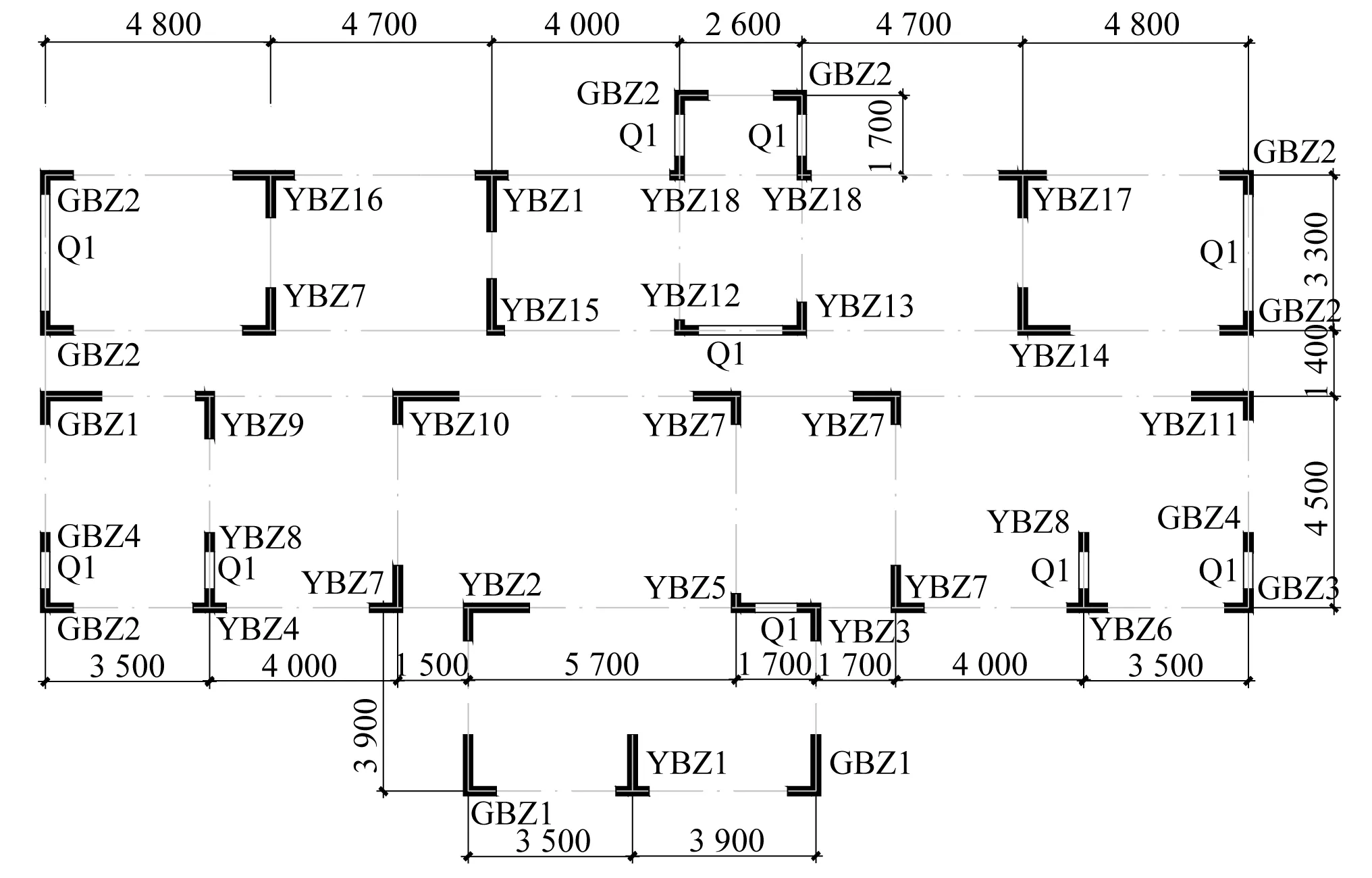
图1 构件图Fig.1 Component diagram

图2 模型施工图Fig.2 Model construction drawing

1.2 试验相似比

动力相似比通过似量纲分析[15]等方法先确定模型的主要参数相似比，再确定其他参数相似比。本文采用大比例尺，全人工质量[16]以更好的与实际模型的受力匹配，各物理量的相似关系如表1所示。

表1 模型相似比Tab.1 Model similarity ratio

1.3 传感器布置

试验主要目的是测试结构各层加速度、位移、扭转、应变等地震响应，在质心布置水平和竖向3个方向加速度传感器30个，在角部布置两个方向拉线位移计12个，联肢墙，长墙布置相应的应变片测试墙体及连梁的受力状态，传感器布置如图3所示。

图3 传感器布置Fig.3 Sensor layout

1.4 地震波加载制度

为研究不同地震动输入对剪力墙结构影响，参考翟长海等[17-18]及GB 50011—2010《建筑抗震设计规范》提出的选波原则，考虑结构的基本周期及波的频谱特性，选择El Centro(Array #9)，Taft (NO. 095)，Wolong (051WCW)3条典型地震动，罕遇地震下的3条地震动输入时程曲线，经归一化的设计反应谱与地震输入反应谱对比如图4所示，选择持时较长的Wolong波主要研究地震输入持时对结构的不利影响。2工况～4工况分别沿结构单向、双向、三向输入El Centro波，其他工况地震动按照原波三向(X，Y，Z)输入到模型中，按照不同设防烈度分38次逐级调整峰值加速度，并分别进行白噪声扫频以研究频率衰减规律，具体加载制度如表2所示。在经历各级地震动地震后，输入7度中震强度，验算余震后模型的地震响应，为以后该类结构的加固与改造提供技术参考。

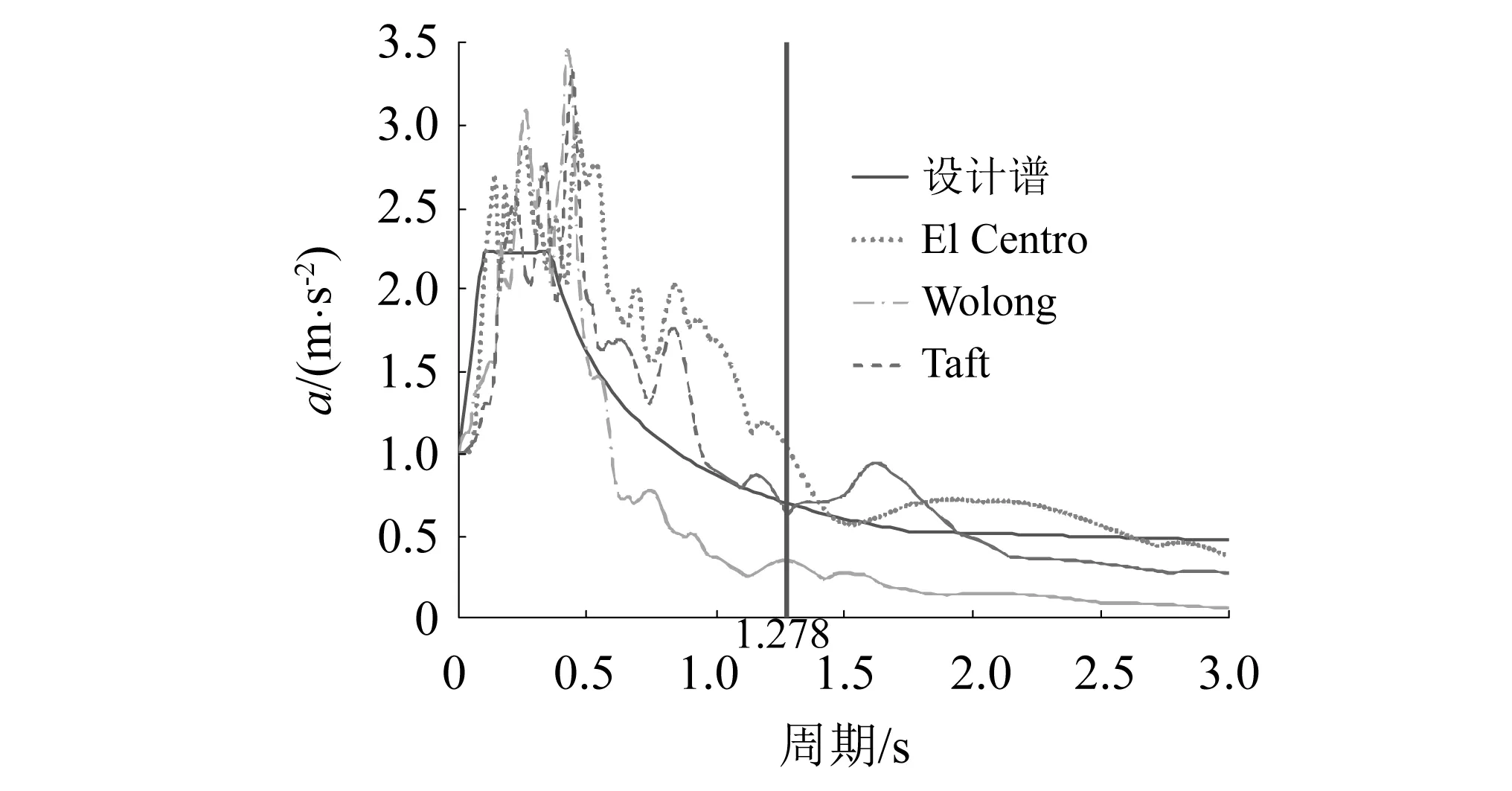
图4 设计谱与地震输入谱对比图Fig.4 Comparison chart of design spectrum and seismic input spectrum

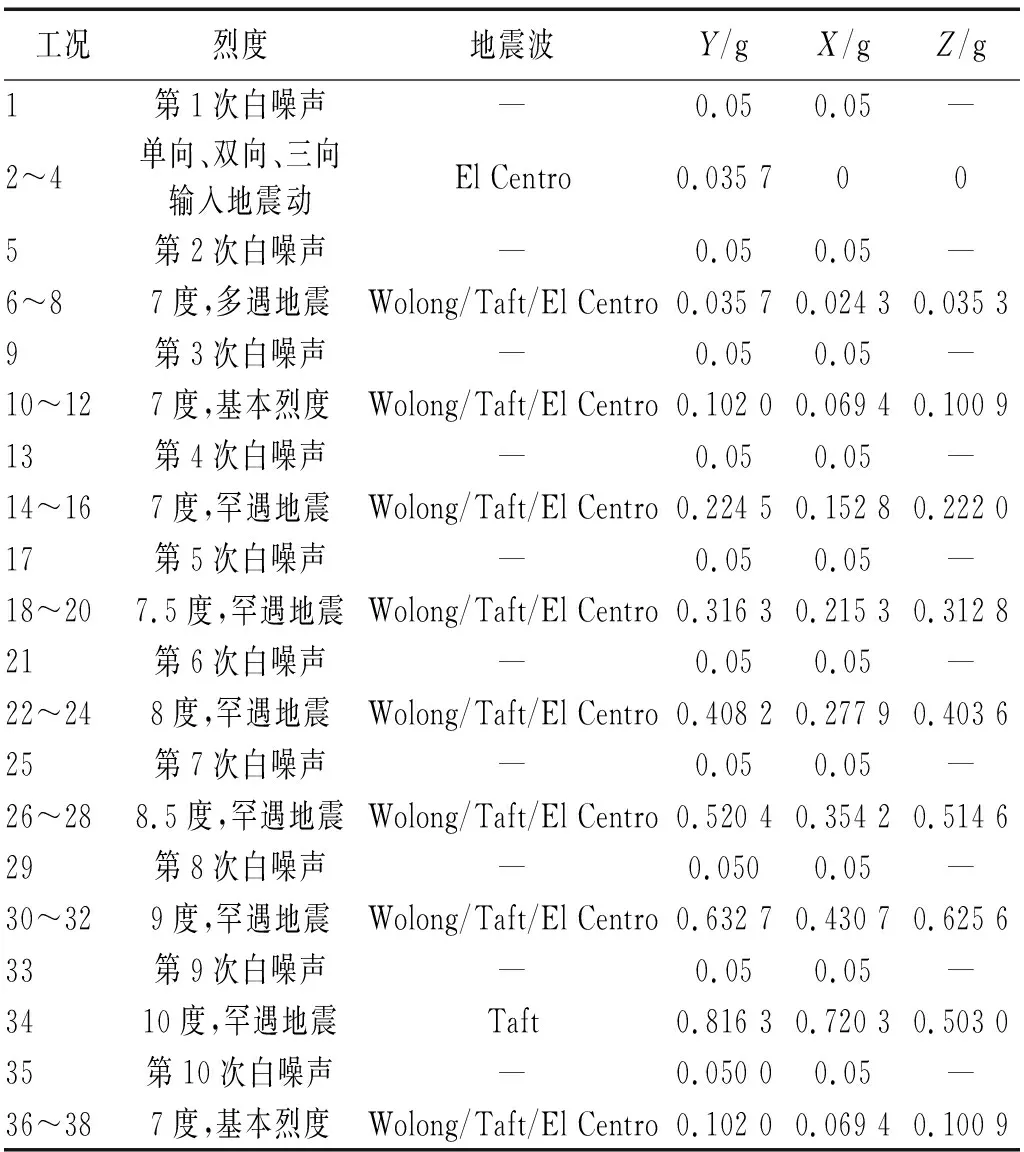
表2 振动台加载工况Tab.2 Vibration table loading conditions

2 模型破坏特征

2.1 刚度退化

试验通过10次白噪声扫频，确定结构在不同地震动输入下的刚度退化规律，研究结构的破坏程度，采用有限元及YJK设计软件分别计算原模型第一周期为1.256，1.278，结构的周期相似比为2.828，得到模型结构的一阶周期理论值分别0.444，0452，通过白噪声扫频由Y向15层、Y向9层、X向15层采集的数据分析得到模型结构的一阶周期分别为0.420，0.438，0.445，最大误差为5.4%，说明原结构与模型结构的周期吻合良好。一阶频率退化趋势如图5所示：结构在经历7度基本烈度后开展第4次白噪声扫频，频率降低不明显说明结构损伤不严重。第5～第7次扫频，结构经历7度、8度罕遇地震后，结构刚度退化较为严重，结构体系中长肢墙出现大量继续延伸的斜向裂缝，短肢剪力墙出现水平弯曲裂缝。第8～第10次扫频，结构刚度退化较慢，结构位移变化明显，构件出现水平和斜向裂缝，混凝土局部出现压溃破坏现象。

图5 一阶频率退化规律Fig.5 First-order frequency degradation law

2.2 试验破坏现象

通过布设128个加速度、位移等传感器对短肢剪力墙结构体系进行全面采集数据，并观察结构的破坏特点，如图6～图11所示。7度多遇地震设防烈度下，主要抗侧力构件GBZ2承受水平地震作用，产生水平裂缝，如图10所示。9度罕遇地震设防烈度下，YBZ11出现与智利地震类似的距离底部约束端的水平通缝，结构的刚度急剧下降，说明结构损伤严重，如图8所示。在8～15工况下，长肢剪力墙主要发生斜向裂缝，结构表现的主要破坏特征为剪切破坏，如图8所示，在20工况后长肢剪力墙结构出现边缘约束构件的水平横向受拉裂缝，连梁产生竖向、斜向裂缝，如图11所示。整体结构的破坏集中分布在9层以下部位，长肢墙的破坏主要分布在1～4楼层，整体结构体系中长肢墙作为抗震第一道防线，有效的耗散地震能量，短肢墙体的破坏并不十分严重。

图6 左侧山墙体整体破坏Fig.6 Overall destruction of the left gable

图7 左侧墙体细部破坏Fig.7 Detail damage of left wall

图8 YBZ11出现的水平通缝Fig.8 YBZ11 horizontal penetrating gap

图9 右侧YBZ2墙体产生塑性铰区Fig.9 Plastic hinge zone on the YBZ2 wall on the right

图10 长墙裂缝开展变化趋势Fig.10 Development trend of long wall cracks

图11 连梁根部产生的竖向裂缝Fig.11 Vertical cracks at the root of the connecting beam

3 试验结果分析

3.1 加速度反应分析

课题组分别按照单向、双向、三向输入峰值加速度为35 Gal的El Centro波并采集各个关键楼层的加速度响应，如图12所示。从试验分析曲线可以看出，在8层、9层加速度有突变，与数值分析结果吻合度很高，分析原因是在8层、9层结构的变形曲线存在一个拐点，是由于在该两层的加速度响应不同导致出现拐点。弹性阶段各个位置传感器测试的加速度的放大系数吻合度很高，说明中国地震局工程力学研究所研制的FBA-12型力平衡加速度传感器可以可靠的测试弹性阶段的建筑物的加速度。从分析的数据看，7度多遇地震作用下，按照单向、双向、三向输入地震动所得各个楼层加速度的响应最大误差在7层，误差值为11.4%，最小误差为1.8%，分布在第5层，各层的平均误差小于10%，其精度在工程领域的多遇地震作用的抗震设计中是足够满足的，因此，在设计某个方向规则的抗侧力构件时可按照单向输入地震动开展相关设计。换言之，对于规则的建筑，在不考虑扭转响应的影响下，可按照单向输入地震动开展弹性阶段设计。进入塑性阶段，考虑损伤影响，扭转效应不容忽视，弹性阶段的结论不能够用于塑性阶段的设计。从分析数据看，1～8层加速度放大在3种输入方式下基本一致或者吻合，8层以上，即拐点以上部分的加速度放大系数对次要方向的地震动输入依赖性较强，对地震动的输入方向的敏感性较高。另外，从地震加速度放大系数分布看，顶层的加速度放大系数为2.6～3.0，顶层结构的层间剪力较大，与华南理工大学周靖关于超高层钢管混凝土重力柱-混凝土核心筒结构振动台试验研究[19]的结果高度吻合，顶层结构的加速度放大系数的表现特性，证明在高层结构设计中顶层墙体的地震剪力要做加强，是否类似鞭稍效应影响尚需进一步研究。

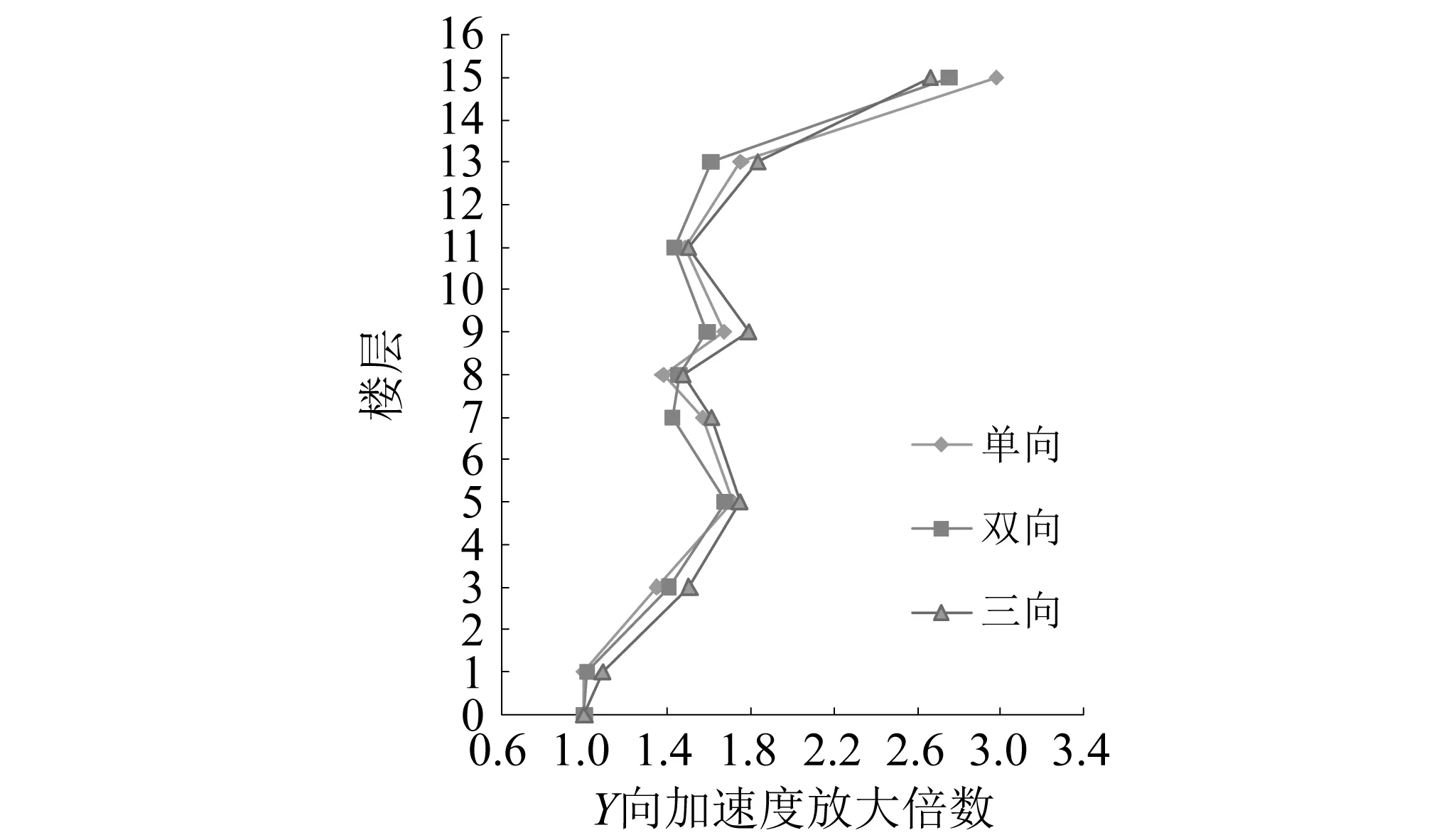
图12 不同输入模式下的El Centro波加速度放大倍数Fig.12 Acceleration amplification factor in different input

如图13所示，由1层、8层、15层各地震波作用下的竖向地震加速度放大的分布数据可以得出，结构在8层竖向地震作用放大系数在2.0～3.5，8层竖向加速度放大系数接近15层竖向加速度放大系数的2倍，结构在9度大震烈度，Taft波、Wolong 波作用下8层的竖向加速度放大系数在3.0～4.3，对于Taft波、Wolong 波下结构经历大震损伤后，7度余震下结构的竖向地震放大作用加大，El Centro波在大震输入下的竖向反应不明显，由数据分析得，结构竖向响应对地震动类型依赖程度很高。由此可得出剪力墙结构在损伤后要考虑中部楼层的竖向地震作用引起的附加重力二阶效应对结构的不利影响，在结构体系经历大震损伤后竖向地震作用会明显增加各个竖向构件的轴力，是在结构损伤后期导致轴压破坏的重要因素。

图13 不同烈度不同地震动输入下结构竖向加速度放大倍数Fig.13 Amplification coefficient of vertical acceleration of structure under different intensities and different ground motions

分析了各个工况下不同地震动峰值加速度放大系数包络图，如图14所示，结构在不同地震动作用下，7度小震和7度中震的加速度放大倍数基本是一致的。7度大震后结构出现不同程度的破坏，结构损伤严重，对应结构第14～第16工况，对应结构第5次白噪声扫频，结构频率降低17.43%，刚度退化严重。与图7所描述的长肢剪力墙结构开始出现斜裂纹破坏描述是一致的。顶层结构的加速度响应的放大倍数在2～3，与El Centro波弹性阶段的顶层放大倍数基本一致。证明高层建筑设计中要充分考虑顶层竖向承重构件的抗剪切承载力的加强。经过7度大震后，由于损伤累计导致结构产生较大的塑性变形，部分砂浆退出工作，结构的层刚度严重退化，结构的位移响应比较明显，结构每层的加速度放大系数明显降低。在9度罕遇地震工况中，El Centro、Taft地震动作用下结构的加速度响应放大倍数小于1，通过第9次白噪声扫频，得出频率降低了58.5%，可见结构整体刚度退化严重。YBZ11出现与智利地震类似的水平剪切破坏通缝。在经过9度大震后，输入7度中震地震动，开展余震下损伤结构体系的研究，由图14所示，损伤后的结构体系整体刚度退化严重，不具备继续承受荷载的能力，必须采取加固措施。结构由于是短肢剪力墙结构，因为较高的配筋率，其延性较好，经历9度罕遇地震后，结构并无倒塌的现象。说明结构可以实现三水准的设计要求，完成7度大震下结构不倒塌的设计要求，证明该结构体系的合理性，具有一定的应用价值。

图14 不同烈度不同地震动输入下各层加速度放大系数Fig.14 Acceleration amplification factor of each layer under different seismic intensity and different ground motion input

3.2 位移反应分析

沿着结构的单向、双向、三向输入峰值加速度为35 Gal的EL Centro波，分析结构的位移响应如图15所示。结构在8层以下，层位移值基本一致，基本不受输入方向的影响。8层以上沿着3个方向输入地震动对结构的位移影响比较大。以7～8层层间位移角为例，结构7～8层在沿单向、双向、三向的层间位移角分别为1/1 721，1/1 520，1/1 410均小于高层技术规程规定的1/1 000，说明该结构体系能较好的满足弹性位移限值要求。两者之间误差最大值为18.07%，说明三向输入地震动对结构的层间位移角影响较大。根据试验数据结果分析，建议高层设计在弹性时程计算中，按照三向地震动输入计算高层建筑结构的位移响应。

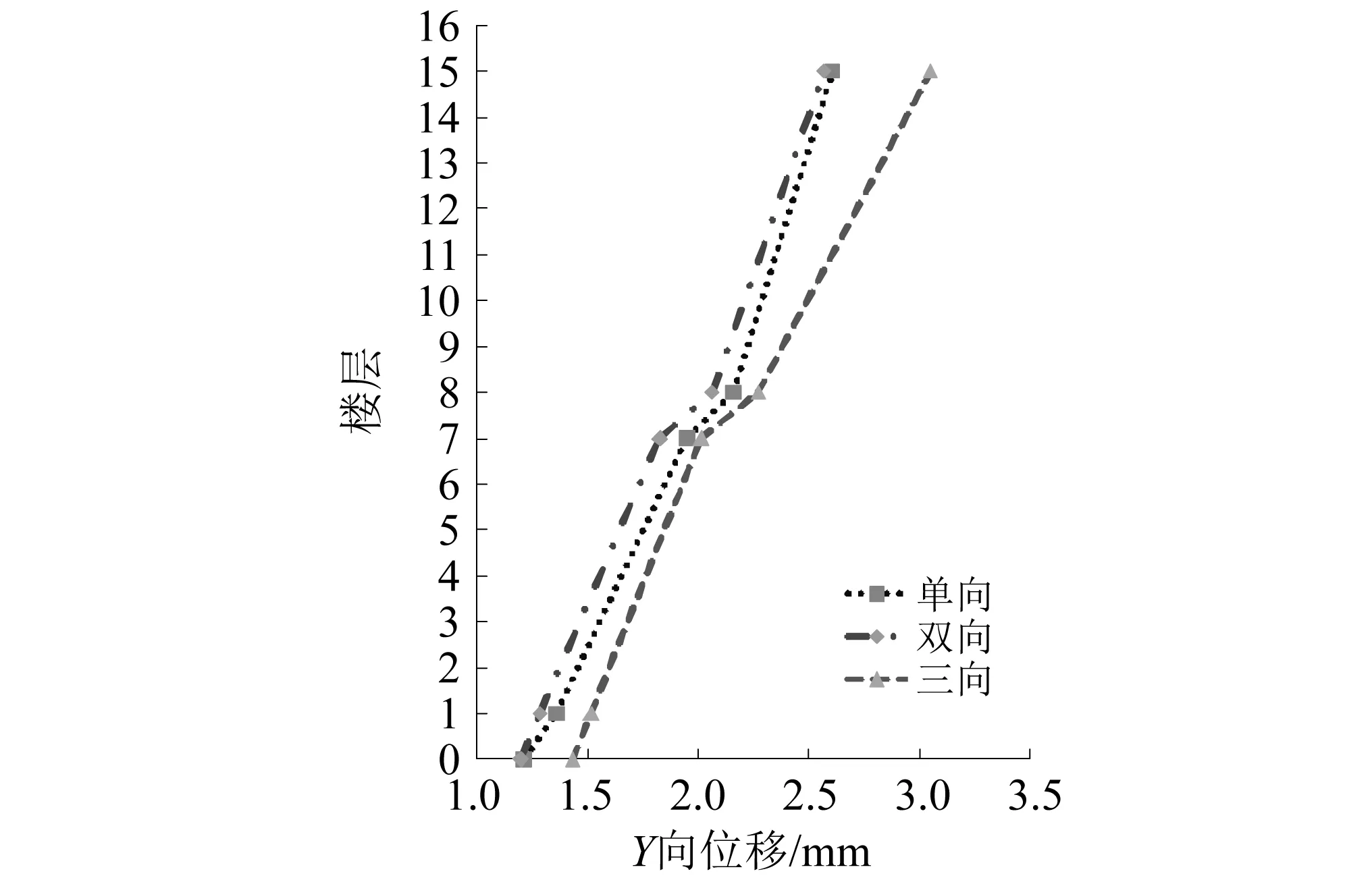
图15 弹性阶段不同输入方式下结构位移响应Fig.15 Structural displacement response under different input modes in elastic stage

研究不同地震动输入下不同烈度的结构位移曲线，由图16分析得到：结构在经历7度大震后结构层间位移产生第一次较大变化，但层间位移角变化并不明显，8度罕遇地震下结构位移较7度烈度位移变化明显，层间位移角明显变大，对应结构第22～第24工况，此刻连梁发生剪切破坏，长肢墙与短肢墙不再协同工作，整体结构刚度降低较快，与白噪声扫频刚度退化的数据一致。9度罕遇地震下的位移角增加显著，最大位移角发生在7层、8层、9层，位移变化量较8度变化梯度减弱，但结构尚未倒塌，说明结构基于性态的设计理念要充分考虑承载能力及使用状态两种设计要求，对结构要基于位移及承载力均要进行严格验算。在El Centro波、Taft波作用下分析横向短肢墙结构体系的位移变化规律，结构在7度小震下仍然处于弹性阶段，7度中震的顶层变形量基本为弹性位移的2倍，7度余震下的位移接近弹性位移的3倍。但是，Wolong波从设计谱与地震动输入谱对比图看，在第一周期处并未包络设计反应谱，从试验结果可以统计出，其弹塑性层间位移角与弹性位移角的差别较大，说明弹塑性位移角与弹性位移角接近的前提是长周期(周期大于0.8 s)、在弱和中等非线性阶段，并且地震动反应谱要包络相对应的设计反应谱，可应用等位移原理。补充了孙景江等[20]提出的等位移原理的假设条件，进一步验证等位移原理的合理性。位移变化曲线与图14描述的加速度变化曲线的变化趋势吻合良好。对于7度余震作用下，3种地震动下的结构位移响应在8层以上的位移变化较大，在8层以下较7度中震下的变形基本一致。说明余震对震后损伤的高层建筑的顶层影响较大，建议严格验算震损后的高层结构顶层位移限值。Wolong波在7度各地震动输入中位移变化基本不明显，从整体结构的位移曲线分析，短肢剪力墙结构属于弯剪型变形曲线，很好的说明长肢墙体作为抗震的第一道防线，短肢剪力墙作为抗震的第二道防线，可以有效的实现抗震的三水准设计要求。

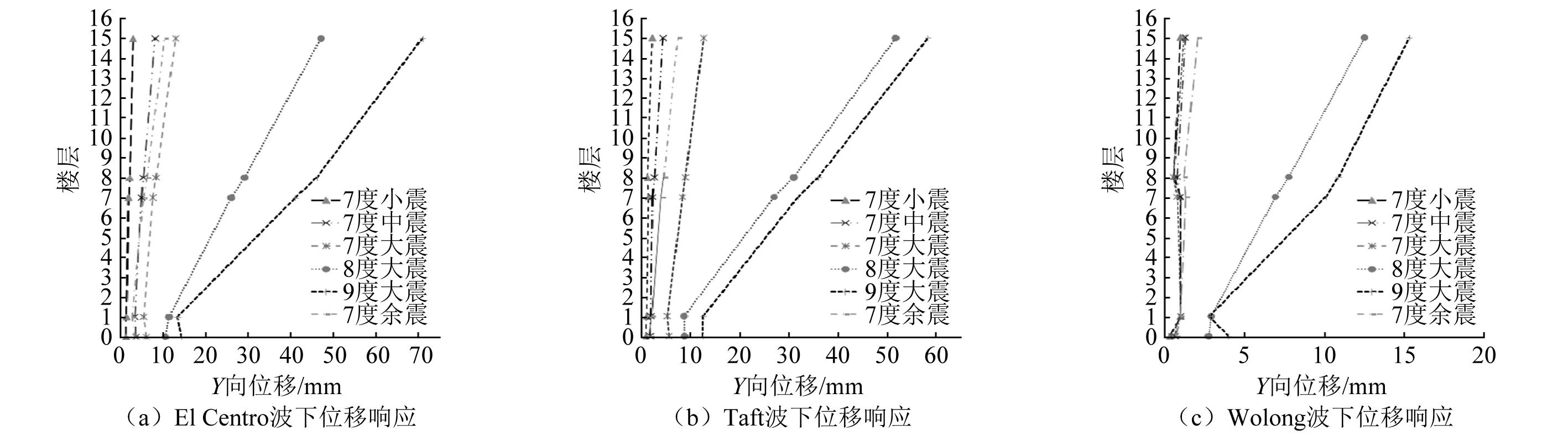
图16 不同地震动输入下结构位移响应分布Fig.16 Displacement response distribution of structure under different ground motion input

按照高层技术规程，剪力墙结构在弹性范围的层间位移角限值为1/1 000，塑性层间位移角限值为1/120，结构体系按照7度设防设计，7层、8层层间位移角试验及数值分析结果，如表3所示。试验与数值分析吻合良好，结果表明该结构体系有较好的抗震性能，层间位移角可以满足结构的规范要求，结构在经历损伤后，余震下的层间位移角依然可满足规范要求，因此可证明该结构体系可以较好的实现基于性态的结构设计要求。

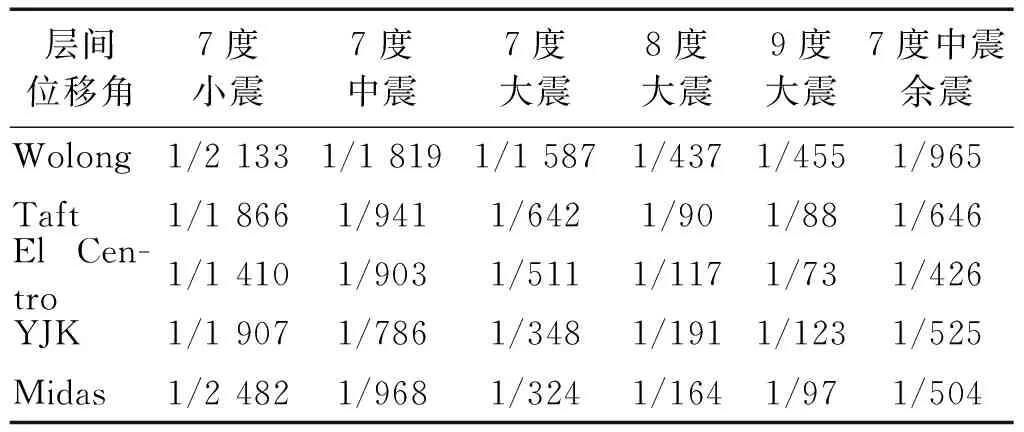
表3 试验及数值分析层间位移角限值对比Tab.3 Comparison of experimental and numerical analysis of displacement angle limits between layers

4 结 论

(1) 通过频谱分析输入3条不同地震动，研究剪力墙结构的刚度退化规律及损伤特点，经扫频得模型周期为0.434，与通过相似准则计算的原结构模型周期0.444基本一致，说明结构可以很好的反演原模型结构的破坏特点，结构在经历7度罕遇地震作用下刚度退化速率较大，对应长肢剪力墙斜向裂缝延伸，短肢墙出现不同的水平弯曲裂缝，连梁端部出现斜向剪切裂缝，墙体不能协同工作，9度地震动输入后，中心部位YBZ11长墙作为抗震第一道防线出现与智利地震类似的墙体剪切破坏通缝。

(2) 7度多遇地震作用下，按照单向、双向、三向输入地震动所得各个楼层加速度的响应最大误差在7层，误差值为11.4%，最小误差为1.8%，分布在第5层，各层的平均误差小于10%，其精度在工程领域的多遇地震作用的抗震设计中是足够满足的。开展竖向地震动放大系数分析，结构在8层竖向地震作用放大系数在2.0～3.5，8层竖向加速度放大系数接近15层竖向加速度放大系数的2倍，结构在9度大震烈度Taft波、Wolong 波作用下8层的竖向加速度放大系数在3.0～4.3。大震下竖向地震动对结构轴向作用不可忽略。开展水平地震动放大系数分析，得出7度小震和7度中震的加速度放大倍数基本是一致的。7度大震后结构出现不同程度的破坏，结构损伤严重，对应结构第14～第16工况，结构第5次白噪声扫频后，结构频率降低17.43%，刚度退化严重。在9度罕遇地震工况中，El Centro波、Taft地震动作用下结构的加速度响应放大倍数小于1，通过第9次白噪声扫频，得出频率降低了58.5%，可见结构整体刚度退化严重。

(3) 结构在7度大震下依然能够满足框架结构的弹性位移限值，在经历8度大震后层间位移角明显变大。试验统计数据进一步证明：在周期大于0.8 s，位移反应在弱和中等线性阶段，地震动反应谱在前几阶周期处能够包络设计反应谱的条件下可应用等位移原理进行弹塑性层间位移角的估计计算。各个工况下结构层间位移角能够很好的满足JGJ 3—2010《高层建筑混凝土结构技术规程》的弹性、塑性限值要求。