汽车转向器非圆齿扇变变位修形过切分析与消除*
2022-06-29丁国龙张力惟
丁国龙,吴 熙,张力惟,向 华
(1.湖北工业大学机械工程学院,武汉 430068;2.国家数控系统工程技术研究中心,武汉 430074)
0 引言
汽车转向器通常采用变速比非圆齿扇齿条副传动,以满足汽车驾驶转向性能要求,其中非圆齿扇齿条副传动一直是重要的研究课题。贺敬良等[1]分析了余弦变比传动规律,唐德威等[2]分析了非圆齿轮副能正确啮合的条件,丁国龙等[3-4]研究非圆齿扇三维数字化建模方法以及非圆齿扇齿廓误差的测量方法。这些理论研究为非圆齿扇的插齿加工研究提供了理论基础。
实际生产中齿轮往往需要修形以改善齿轮传动性能,在汽车转向器非圆齿扇变变位修形加工过程中,长期存在齿廓过切现象,导致实际鼓形量偏小,达不到理论设计值。实际生产中企业往往凭借经验,反复试凑非圆齿扇齿廓鼓形量,生产效率低,精度不高。因此,研究非圆齿扇的修形过切对改善实际生产状况有着重要意义。樊智敏等[5]发现在齿轮实际加工中啮合干涉会导致过切现象的发生。丁国龙等[6]研究了转向器非圆齿扇加工方法,基于华中8型数控系统开发了插齿专机系统。熊镇芹等[7]基于插齿加工的退刀干涉现象,提出了回转中心偏离法解决问题。李丽萍、陈鑫烨[8-9]分析了刀具补偿半径对加工过切的影响,发现了不同的刀具补偿方法能缓解过切。唐德威、党兰焕、韩华等[10-12]根据非圆齿扇加工过程,分析了尖顶、根切、负啮合、过切等影响加工质量的常见因素,提出了一些可行性措施,但由于过切量较小,影响因素多,只能减少过切现象发生。BAIR等[13]研究了使用圆弧齿条刀具对椭圆齿轮进行加工时,椭圆齿轮的两长轴端齿根处因中心距变化而产生的根切现象。上述研究对解决汽车转向器非圆齿扇修形过切问题提供了很好的思路和借鉴。
针对上述问题,从运动学上分析了汽车转向器非圆齿扇变变位修形加工过程,计算了实际加工的非圆齿扇齿廓,基于理论齿廓方程提出了反求齿条刀具的过切消除方法,为改善非圆齿扇变变位修形加工提供新的思路。
1 非圆齿扇变变位修形运动分析
1.1 变变位修形原理分析
非圆齿扇变变位修形加工在三轴联动的数控插齿机完成,如图1a所示。以齿条刀具上下冲程运动为主运动,径向进给轴为Y轴,水平移动轴为X轴,工件旋转轴为C轴。其中展成运动由X、C轴按给定的变传动比曲线完成,修形运动由Y、C轴按给定的分段线性修形函数完成,展成运动与修形运动同时完成。修形运动时,齿条刀具沿Y轴进、退刀运动加工变变位修形鼓形量,其修形函数曲线如图1b所示。
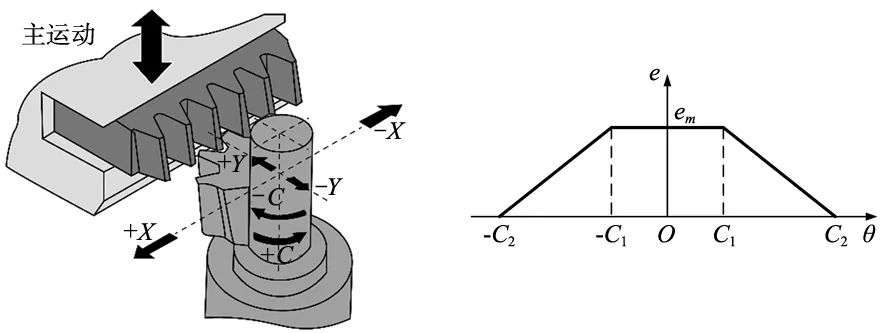
(a) 非圆齿扇修形加工运动示意图 (b) 分段线性函数修形曲线
修形量e是齿扇转角θ的函数,函数表达式为:
(1)
式中,em为最大修形量;C1、C2为线性变化起始角和终止角。
理论上,每一个齿扇转角θ对应一个修形量e。在齿扇转角θ∈[C1,C2]时,取若干个转角值,如图2a所示,取区间内10个转角值-d5~d5,其中d1=C1,d5=C2。根据式(1)计算各转角对应的修形量,将修形量e沿啮合点公法线方向转化成鼓形量esinφ,φ为对应点的齿扇转角,e1~e5为对应角度的鼓形量,在修形加工过程中,希望得到如图2b所示的鼓形齿廓,即在[C1,C2]范围内齿厚增加的部分。
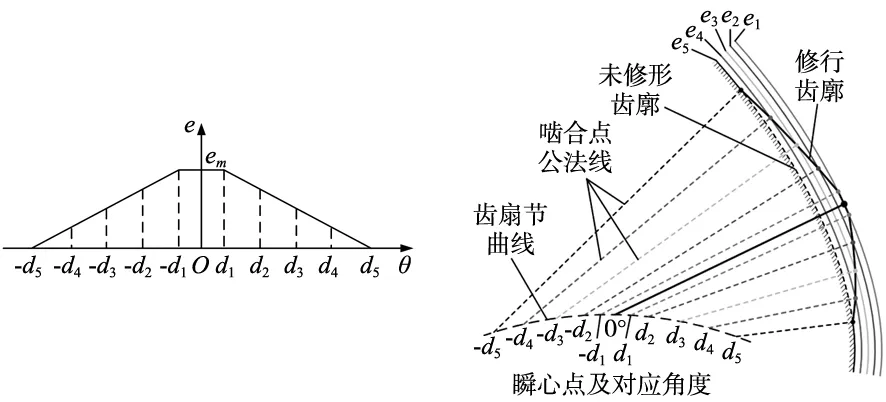
(a) 修形量与齿扇转角关系示意图 (b) 齿廓法向鼓形量叠加示意图
1.2 余弦变传动比传动分析
常见的变传动比有:梯形变比、余弦变比、多项式变比和反向变比等。其中余弦函数变传动比曲线如图3所示。
图3 余弦变传动比函数曲线
余弦变比的传动比函数如下:
(2)
1.3 非圆齿扇变变位修形理论齿廓方程求解
无修形时,根据齿轮的啮合原理得,齿扇齿条副的啮合瞬心点K0在齿扇和齿条的连心线上,因此OK0即为齿扇旋转一定角度θ时的瞬心半径r0,r0的计算表达式如下:
(3)
式中,L0为滚珠丝杆的导程;i为转向器的传动比。
已知齿条刀具齿廓(xt,yt,1)T,根据齿轮啮合原理,计算无修形非圆齿扇齿廓坐标(xg,yg,1)T的公式为:
(4)
式中,d表示齿扇坐标系与刀具坐标系的距离;l表示刀具水平方向移动的距离。
根据式(4)将修形量e沿无修形的非圆齿扇公法线方向叠加,如图2b所示,得到变变位修形的理论齿廓坐标方程:
(5)
1.4 非圆齿扇变变位修形实际齿廓方程求解
变变位修形过程,即齿条刀具沿y轴进、退刀过程,如图4所示。
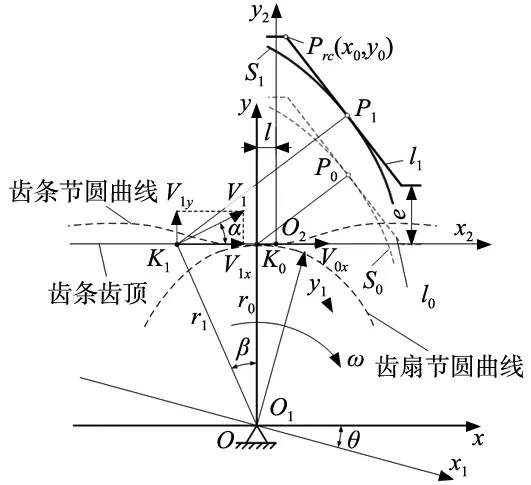
图4 变变位系数修形的啮合运动分析
图中点K0和K1分别为无修形时和变变位修形时齿扇齿条啮合的瞬心点;P0和P1分别为相同转角下无修形和变变位修形的啮合点。图中详细符号说明如表1所示。过变变位修形瞬心点向齿扇齿条副连心线作垂线,设ɑ为V1与x轴夹角,即为速度方向和垂线夹角,β为OK1与y轴夹角,则β为ɑ的外切角,β=ɑ。OK1为瞬心点与齿扇回转中心点连线。
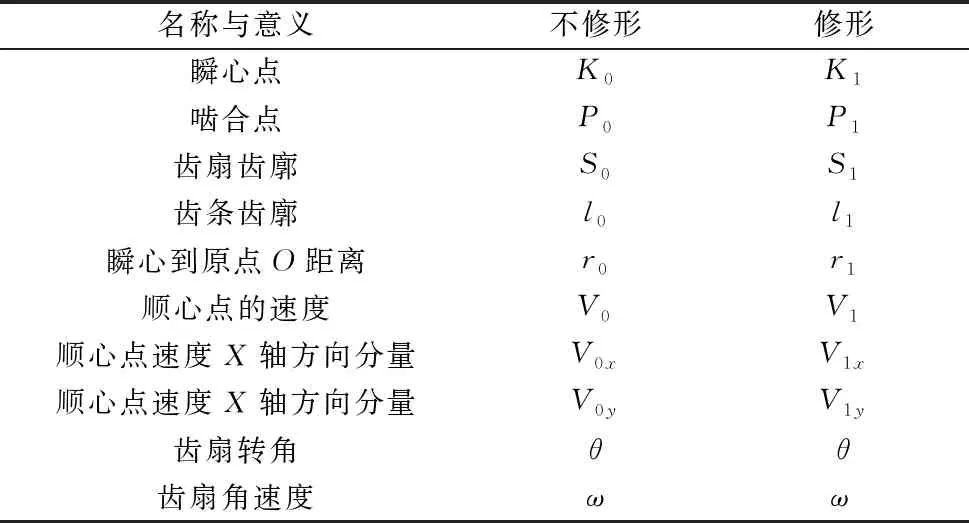
表1 符号说明
无修形时,齿条节曲线与齿扇节曲线的切点即为瞬心点,瞬心点K0始终在齿扇与齿条的连心线上,即K0点在y轴上。K0水平方向速度为V0x,大小为:
V0x=r0ω
(6)
式中,ω为齿扇旋转角速度。
变变位修形时,齿条刀具增加了径向速度V1y,水平速度V1x没有改变,因此:
(7)
V1x=V0x=r0ω
(8)
根据速度三角形法,代入式(6)~式(8)可得:
(9)
根据式(9)可得无修形瞬心半径和变变位修形瞬心半径的关系为:
r1cosβ=r0
(10)
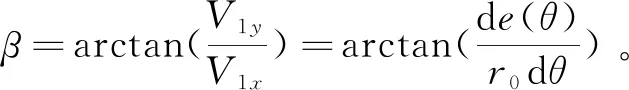
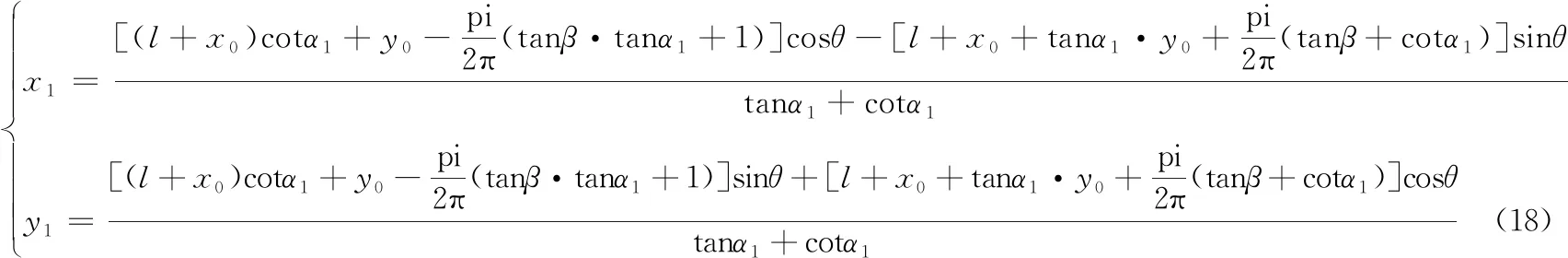
式(10)表明,变变位修形加工的任意时刻,从变变位修形瞬心点K1向齿扇齿条副连心线作垂线,垂足正是无修形瞬心点K0,即齿扇中心点、变变位修形瞬心点和无修形瞬心点构成一个直角三角形。变变位修形瞬心点始终在无修形瞬心点沿x轴负方向的延长线上,在齿条刀具沿y轴进退刀加工变变位修形鼓形量时,瞬心点位置沿x轴水平方向移动。
根据分段线性修形曲线表达式(1),得:
(11)
在RtΔOK1K0中,瞬心点K1(xk1,yk1)在定坐标系中的坐标为:
(12)
将式(6)、式(10)和式(11)代入式(12)整理得瞬心点K1(xk1,yk1)的坐标如下:
(13)
根据齿廓法线法,齿扇和齿条的啮合点就是公法线与公切线的交点,所以啮合点坐标可由公法线和公切线方程联立求解。
在图4中,设P1(x,y)为啮合点,Prc(x0,y0)为齿条齿廓上的一个已知点,公法线为K1P1,公切线为P1Prc,即齿条刀具齿廓线。
公切线P1Prc方程为:
y-y0=tan(α1+π/2)(x-l-x0)
(14)
式中,α1为齿条上参与啮合的齿廓的压力角。
公法线K1P1方程为:
y-yK1=tanα1(x-xK1)
(15)
联立式(14)和式(15),计算出啮合点在定坐标系下的坐标为:
(16)
式(16)为啮合点P1在定坐标系[O0,x0,y0]中的轨迹方程。
将P1变换到齿扇坐标系[O1,x1,y1]中,则:
(17)
代入式(16)得:
式(18)即在齿扇坐标系[O1,x1,y1]下变变位修形实际齿廓坐标方程。
2 反求齿条刀具消除过切
2.1 反求刀具齿廓方程
式(5)为变变位修形非圆齿扇理论齿廓坐标方程,即非圆齿扇齿廓在没有发生过切的理论情况下的齿廓方程。
在图3中,齿条刀具在y轴上的移动量为l。理论非圆齿扇齿廓坐标在齿扇坐标系[O1,x1,y1]下的坐标为(xg,yg),坐标系[O2,x2,y2]到坐标系[O1,x1,y1]的变换表达式为:
(19)
将式(19)改写为矩阵形式,可得:
(20)
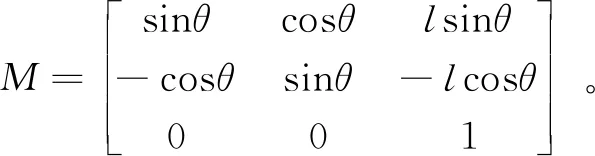
现已知[O1,x1,y1]坐标系求[O2,x2,y2]坐标系下的坐标,则需转换成如下表达式:
(21)
齿廓曲线和共轭齿条模型是根据齿轮啮合原理按照节曲线做纯滚动,如果已知其中任意一个齿廓坐标,即可通过坐标变换推导出另一个齿廓坐标,因此根据以上坐标变换可由理论非圆齿扇坐标得出其共轭齿条的齿廓坐标,理论非圆齿扇与生成齿条间的无齿侧间隙啮合方程为:
rt=M-1(rg-rd)
(22)
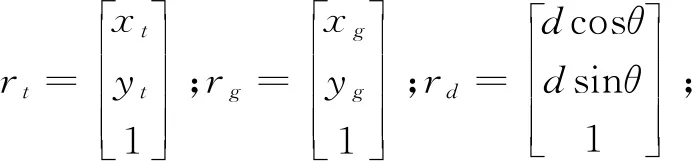
化简得以理论的非圆齿扇齿廓反求的齿条刀具齿廓方程为:
(23)
2.2 用反求刀具加工非圆齿扇
齿条刀具如图5所示,各参数取值如表2所示。
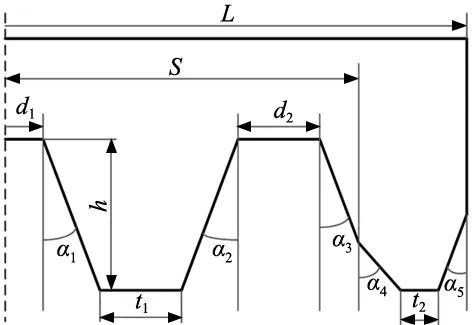
图5 刀具示意图
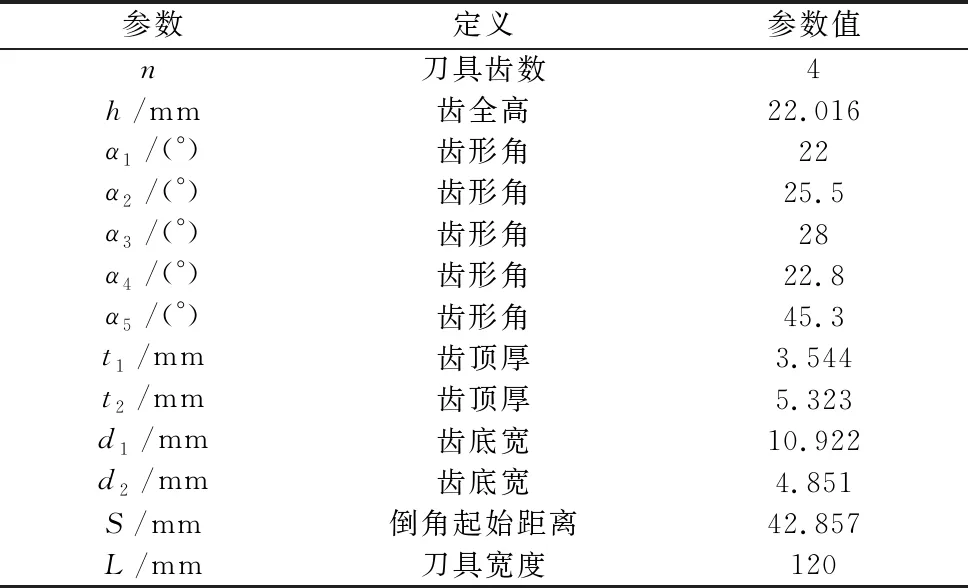
表2 齿条刀具的参数
传动比模型为余弦函数变比传动,其函数图像如图3所示,传动比参数如表3所示。

表3 传动比参数
变变位修形函数图像如图1b所示,齿扇修形参数如表4所示。

表4 齿扇修形参数
余弦变比非圆齿扇的工件参数如表5所示。

表5 工件参数
将实际修形齿廓、无修形齿廓和理论修形齿廓进行对比,对比图如图6所示。将齿扇转角在-5°附近的齿廓放大,可以明显看出实际修形齿廓的鼓形量小于理论齿廓鼓形量,因此实际加工中存在过切现象。
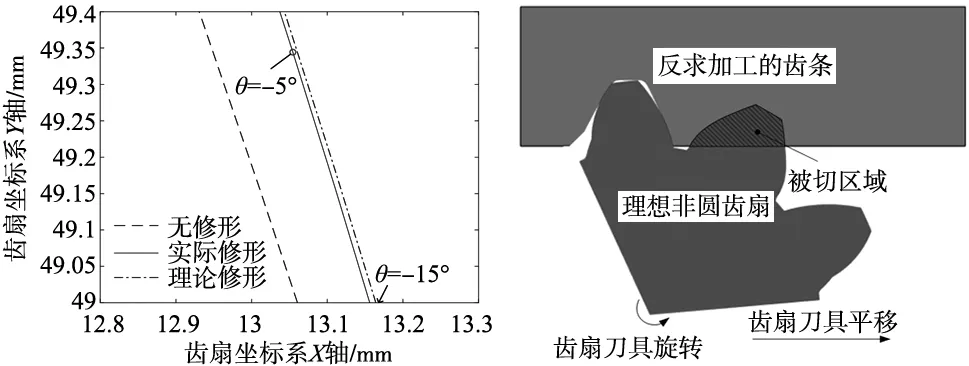
图6 三种齿廓对比图 图7 反求齿条刀具啮合运动示意图
根据齿廓展成原理,利用理论齿扇齿廓反求齿条刀具齿廓,反求加工过程仿真如图7所示。
反求齿条刀具齿廓如图8所示,与原普通齿条刀具齿廓对比,反求齿条刀具齿廓的齿廓中部有明显内凹。
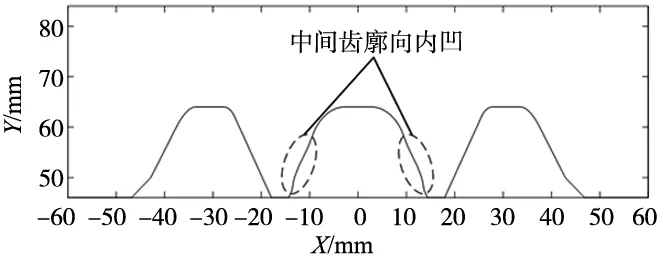
图8 反求齿条刀具齿廓图
用反求齿条刀具加工变变位修形非圆齿扇的过程如图9所示。
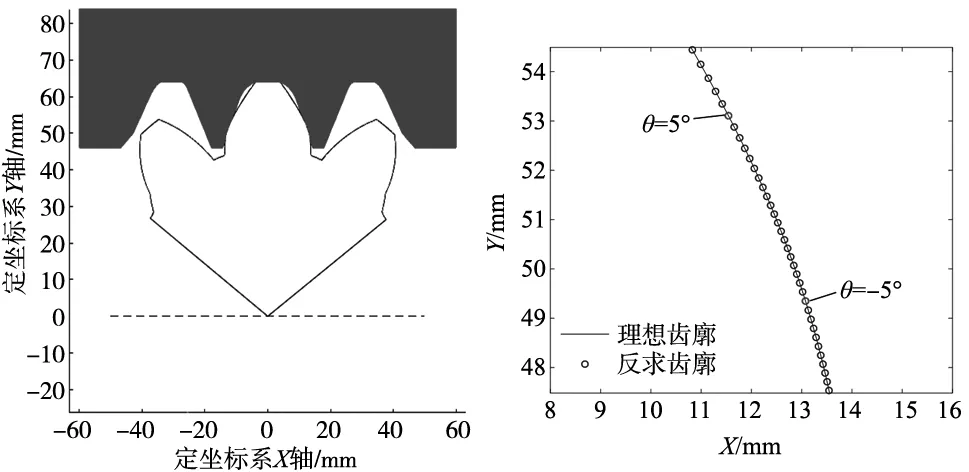
图9 反求齿条刀具加工非圆齿扇示意图 图10 反求齿条刀具加工的非圆齿扇齿廓与理论齿廓对比
其可看成齿条齿扇无侧隙纯滚动啮合过程,齿条刀具不需要沿y轴进、退刀。将加工后的齿扇齿廓与变变位修形理论齿廓对比,结果如图10所示。
可以看出,两种齿廓重合,鼓形量相等,彻底消除了加工过程中的过切。
3 结论
(1)变变位修形的任意时刻,齿扇回转中心点、变变位修形瞬心点和无修形瞬心点构成一个直角三角形,该规律是计算变变位修形啮合瞬心点位置和速度的基础。
(2)提出了一种反求齿条刀具的计算方法,用反求的刀具加工非圆齿扇,可以消除非圆齿扇修形中的过切,通过仿真验证了算法的正确性。
