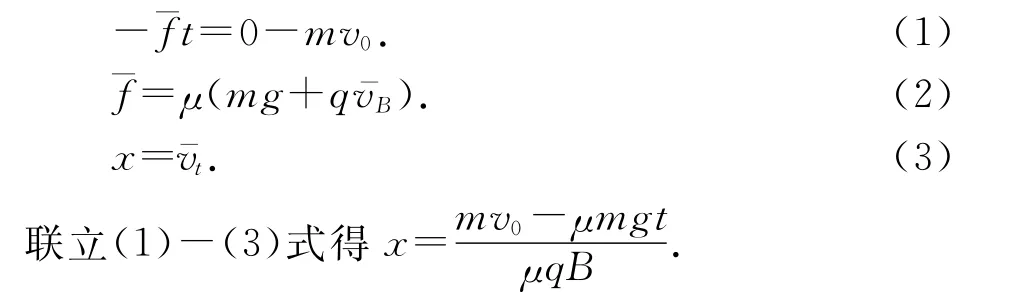洛伦兹力的冲量特点在带电粒子运动中的应用

朱玉元

（福州一中，福建福州 350001）

带电粒子在洛伦兹力作用下的运动问题，往往对学生的数理结合能力要求较高，因此也是高考的常考点和难点.在这类问题中，不论是单纯的有界磁场，还是组合场或者复合场的情境下，洛伦兹力都对带电粒子的运动发挥着重要影响.在日常授课中，教师多从洛伦兹力提供向心力的角度，通过画轨迹定圆心求半径的流程来解决问题，而洛伦兹力的冲量特点较少被提及.本文尝试利用洛伦兹力的冲量特点，从动量定理角度来分析带电粒子的运动.

1 洛伦兹力的冲量特点

我们知道洛伦兹力与粒子的速度有关，其在两个相互垂直方向上的分力的冲量大小分别为

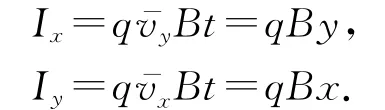
在仅受洛伦兹力的作用时，根据动量定理可得

即利用洛伦兹力冲量的特点可以得到带电粒子在某一方向动量变化量与垂直该方向位移成正比.利用这个关系解决问题只需抓初末状态，可以免去分析运动细节（如找圆心、求半径等几何关系）的困难，使问题简化.

2 用动量定理分析带电粒子在匀强磁场中的运动

2.1 在匀强磁场中圆轨迹的证明

解析：如图1所示，在磁感强度为B的匀强磁场中，质量为m、带电量为＋q的不计重力的带电粒子，以速率v从原点O向x轴正方向射出.可以把粒子运动过程所受洛伦兹力沿x轴和y轴正交分解，即fx＝qvyB，fy＝qvxB.粒子从原点O到轨迹上任意点A（x，y）的过程中，在x、y两个方向上，根据动量定理得

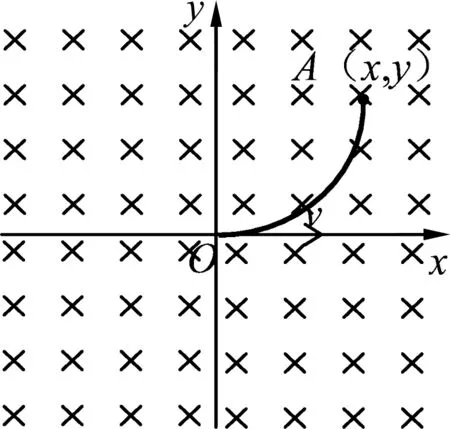
图1

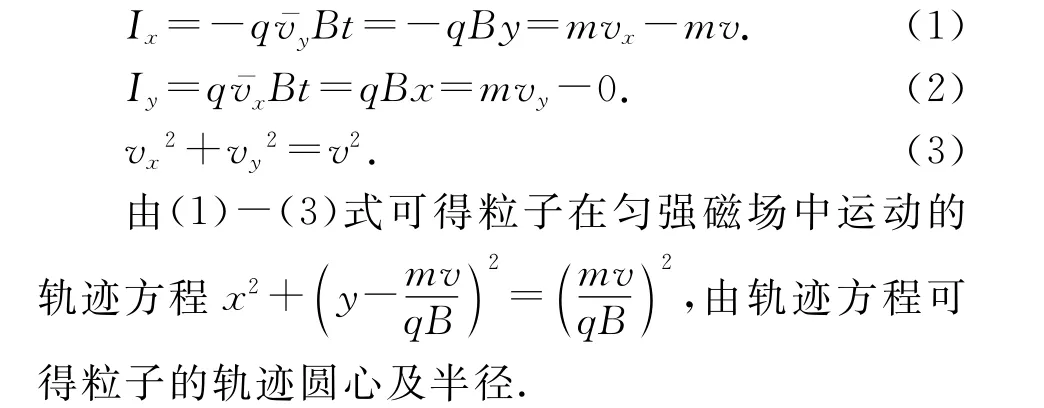
对于重力不计的带电粒子垂直进入匀强磁场中的运动轨迹为什么是圆，一般教师的处理方式是先用洛伦兹力演示仪观察其运动轨迹，再定性说明其向心力就是洛伦兹力.这种方式并不能让一些爱思考的学生“完全信服”，不妨试试通过动量定理来证明，提升知识的严谨性并拓展学生的思路.

2.2 关注始末状态舍弃复杂的几何关系

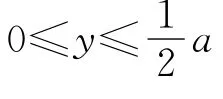
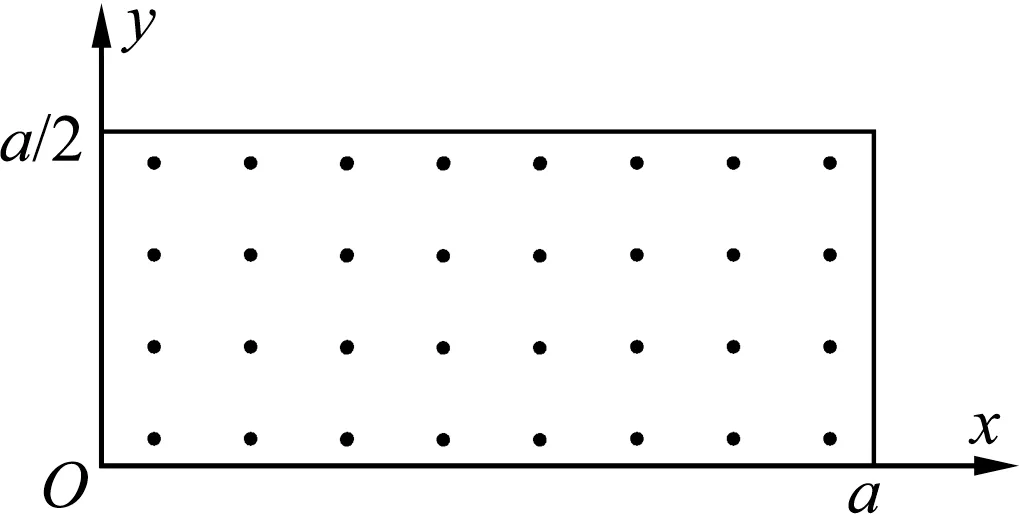
图2

解析：由几何关系可知最后离开磁场的粒子运动轨迹如图3所示，设粒子入射速度与y轴夹角为θ，轨迹与磁场上边界切点为B，出射点为C.

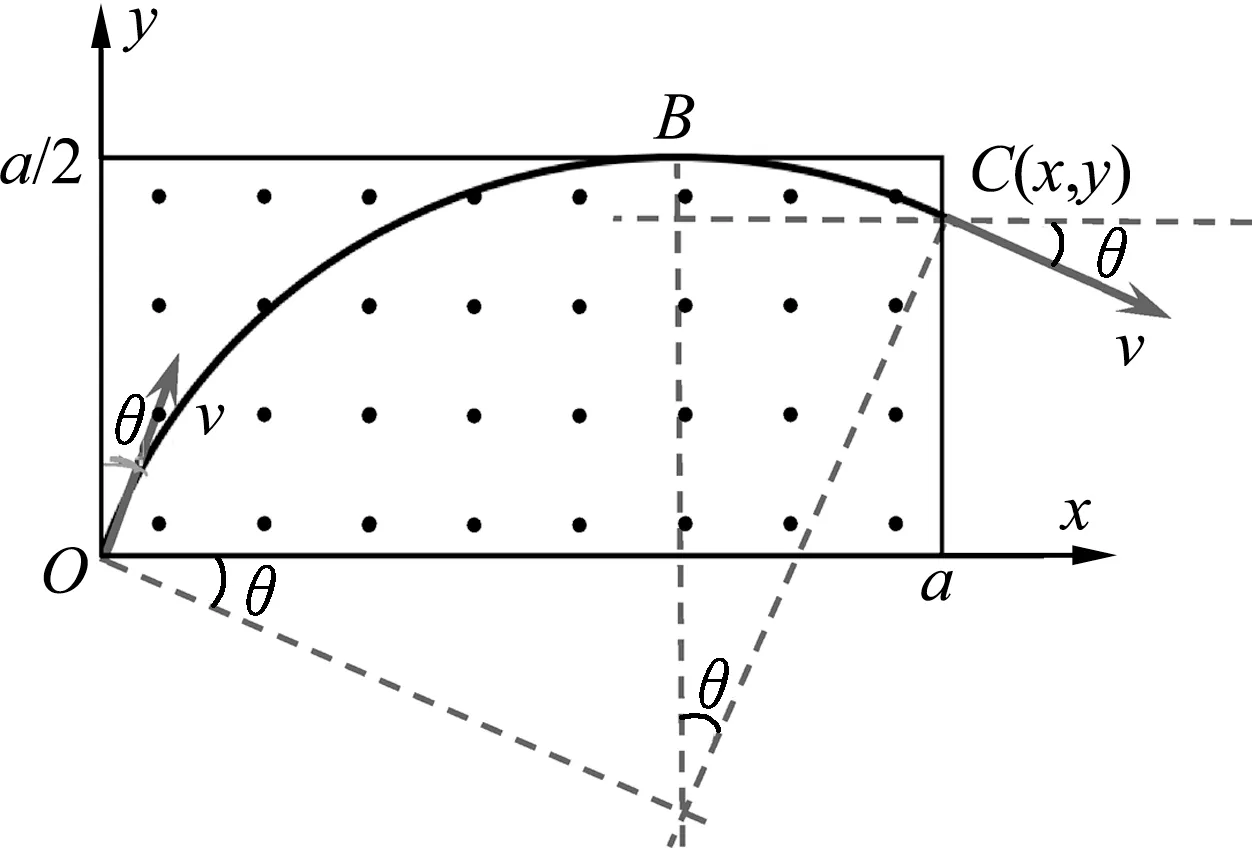
图3

O→B过程中，沿x方向由动量定理得

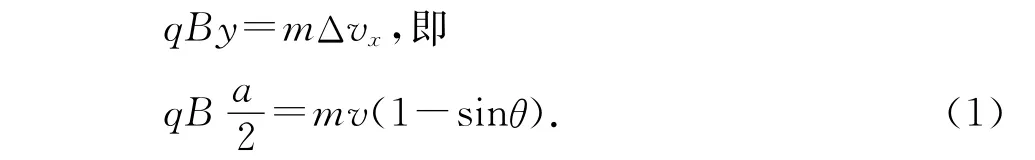
O→C过程中，沿y方向由动量定理得

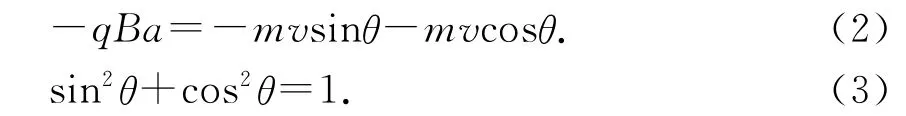
由（1）－（3）式得

表中展现了本文对政府引导基金融资模式的探索性评价结果，数值越高表明对应的能力越强，对应的压力越大。表中的评价结果主要基于是否直接投资和是否股权投资两个维度所得，表中直观地展现出了政府引导基金不同模式在撬动社会资本、政府意愿体现、政府参与公司治理能力和多阶段投资引导能力上的差异。

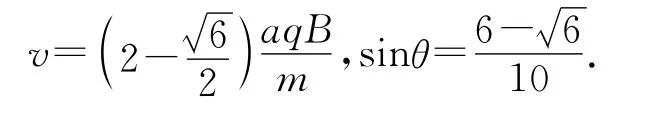
在匀强磁场中，若发现已知条件中包含“距离”、“速度变化”等信息时，通过应用两个相互垂直方向上的动量定理比用普通几何方法会更便捷.

2.3 磁聚焦模型的动量分析

图4

解析：由题意可知粒子的轨迹半径r等于磁场半径R，任取一个粒子作为研究对象，设该粒子的入射点P的坐标为（x，y），粒子的出射点Q的坐标为（x0，y0），如图5所示.

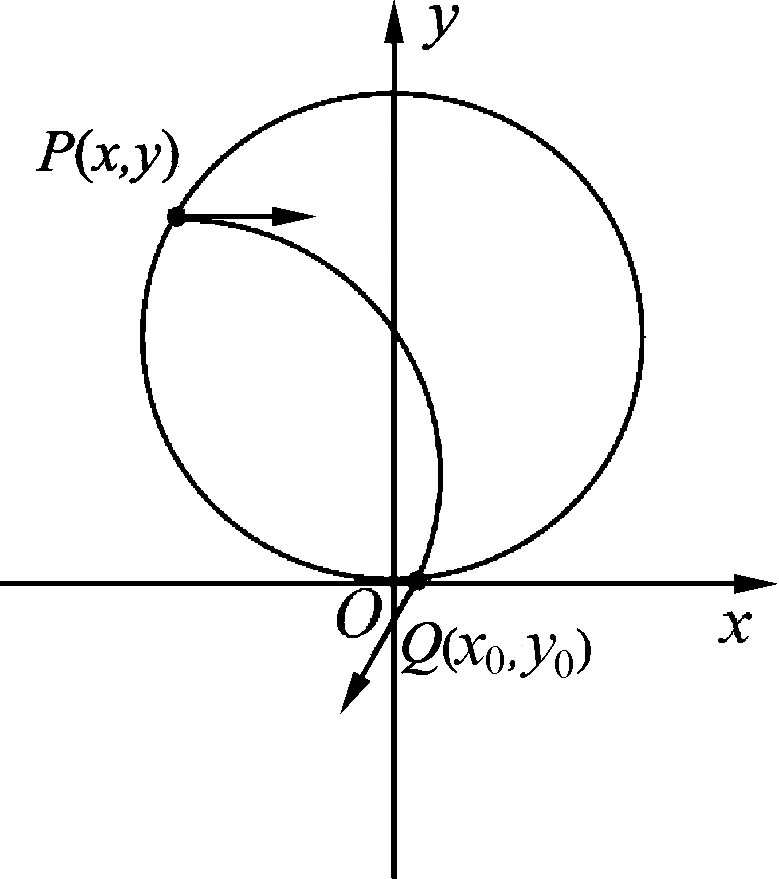
图5

由x、y两个方向的动量定理可得

由（1）－（5）式解得

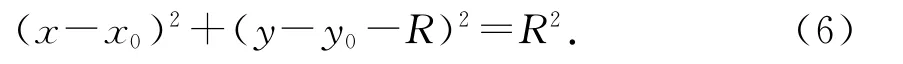
又因为

则由（6）、（7）式得x0＝0，y0＝0，即这束带电微粒都通过坐标原点O.

2.4 扭摆模型的动量分析

例4.（2011 年山东高考题节选）扭摆器是同步辐射装置中的插入件，能使粒子的运动轨迹发生扭摆.其简化模型如图6：Ⅰ、Ⅱ两处的条形匀强磁场区边界竖直，磁场方向相反且垂直纸面.一质量为m、电量为－q、重力不计的粒子经电场加速后平行于纸面射入Ⅰ区，若B1≠B2，L1≠L2，且已保证了粒子能从Ⅱ区右边界射出.为使粒子从Ⅱ区右边界射出的方向与从Ⅰ区左边界射入的方向总相同，求B1、B2、L1、L2之间应满足的关系式.

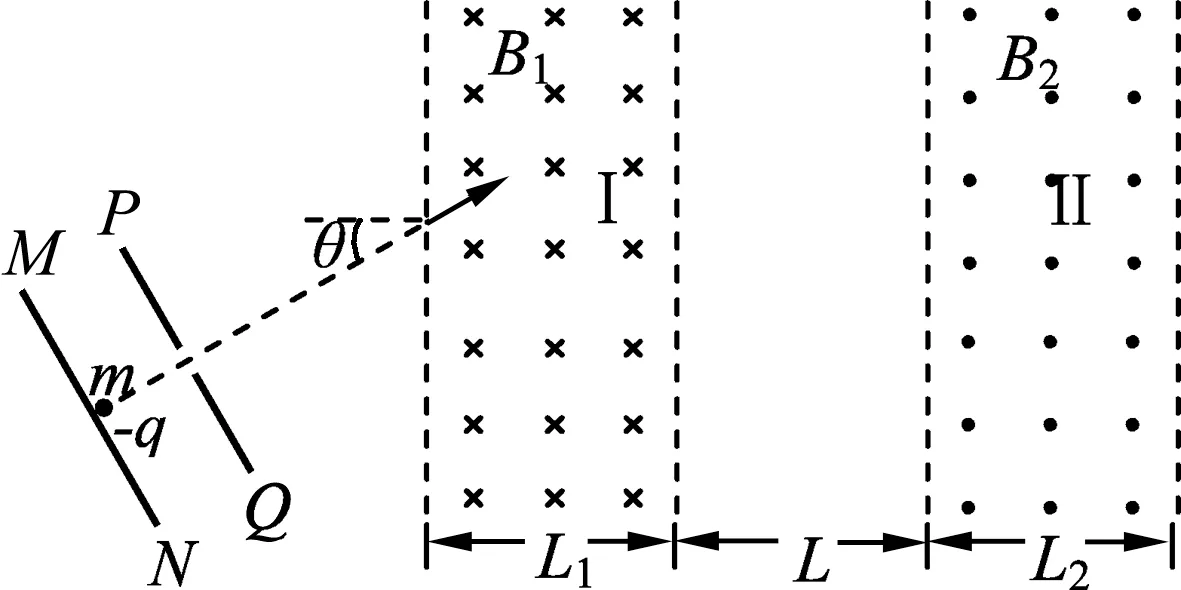
图6

解析：在粒子穿过两个磁场的过程中，分别沿y方向利用动量定理，可得经过B1：

经过B2：

由题意知，穿过两个磁场后速度方向不变（图7），即

图7

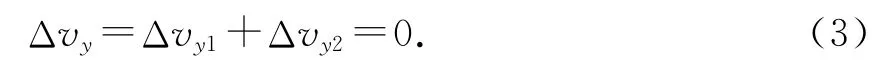
则由（1）－（3）式得qB1x1＝qB2x2，又x1＝L1，x2＝L2，可得B1L1＝B2L2.

在这个问题中如果用几何关系来处理很麻烦.分析发现题意中涉及到速度变化量与沿某一方向粒子通过的距离，因此利用洛伦兹力冲量的特点通过动量定理将二者联系起来.

3 用动量定理分析带电粒子在组合场或复合场中的运动

例5.如图8所示，两导体板水平放置，两板间的电势差为U，带电粒子以某一初速度v0沿平行于两板的方向从两板正中间射入，穿过两板后又垂直于磁场方向射入边界线竖直的匀强磁场，则粒子射入磁场和射出磁场的M、N两点间的距离d随着U和v0的变化而变化情况为

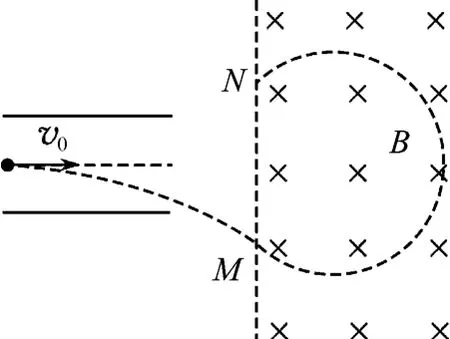
图8

（A）d随v0的增大而增大，d与U无关.

（B）d随v0的增大而增大，d随U的增大而增大.

（C）d随U的增大而增大，d与v0无关.

（D）d随v0的增大而增大，d随U的增大而减小.

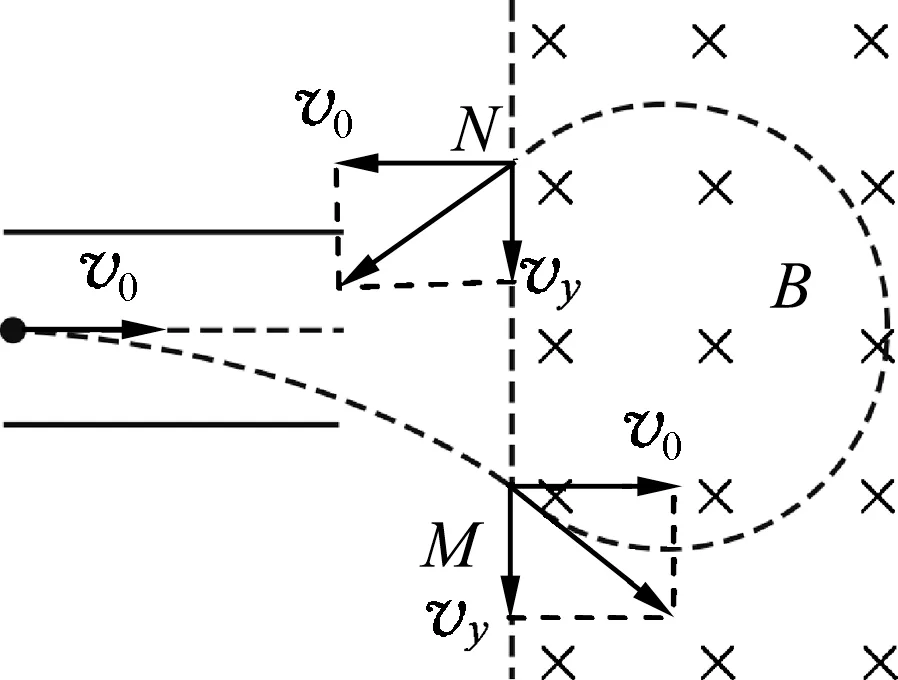
图9

这些粒子轨迹的弦长之所以相等，并不是简单的数学巧合，而是它们沿x方向动量变化量相等造成的.在这种组合场问题中，在类平抛、直线边界磁场的情境下，动量定理的解法相比与普通几何解法更加简洁且贴近物理本质.

例6.（2015 年天津高考题节选）现代科学仪器常利用电场、磁场控制带电粒子的运动.真空中存在着如图10 所示的多层紧密相邻的匀强电场和匀强磁场，电场与磁场的宽度均为d.电场强度为E，方向水平向右；磁感应强度为B，方向垂直纸面向里，电场、磁场的边界互相平行且与电场方向垂直.一个质量为m、电荷量为q的带正电粒子在第1层电场左侧边界某处由静止释放，粒子始终在电场、磁场中运动，不计粒子重力及运动时的电磁辐射.粒子从第n层磁场右侧边界穿出时，速度的方向与水平方向的夹角为θn，试求sinθn的大小.

图10

解析：设粒子在第n层磁场中运动的速度为vn，从第n层磁场右侧边界穿出时速度方向与水平方向的夹角为θn，由动能定理和图11可得

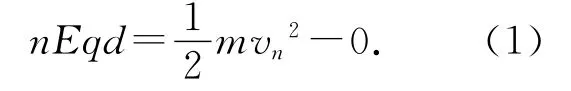
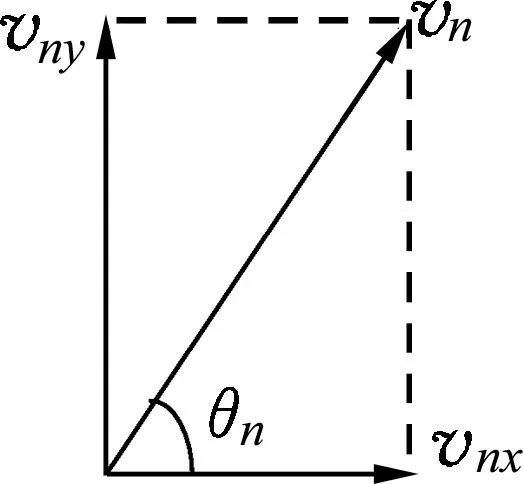
图11

粒子在电场中运动时，y轴的速度分量不变，只有在磁场中y轴的速度分量发生变化，在粒子从开始到穿出第n层磁场过程中，由动量定理可得

在这类多个平行边界磁场与电场的组合场情境下，因粒子进入每层磁场的速度大小方向都不同，如果运用传统几何方法求解过程会比较复杂繁琐，而利用电场力改变小球合速度大小、洛伦兹力分力的冲量改变小球垂直电场力方向的动量的特点，利用动量定理抓住初末状态，过程就显得清晰且简洁.

洛伦兹力的冲量特点之所以有如此妙用，其本质源于洛伦兹力的大小与速度大小成正比，在高中物理范围内，还有其它力也有类似的特点，对它们的冲量进行分析，也会得到相似的结论.

4 其它F＝F 0＋kv的情况

例7.如图12，质量为m、带电量为＋q的小滑块与水平面间的动摩擦因数为μ，匀强磁场的磁感应强度大小为B，方向水平向外，给滑块一个向右的水平初速度v0，经过时间t速度减为0，已知重力加速度为g，求此过程滑块的位移大小x.

图12

解析：对滑块进行受力分析，受力图如图13所示，在摩擦力作用下滑块做减速运动，其洛伦兹力减小导致摩擦力也减小，其摩擦力与速度成线性关系，我们可以通过摩擦力的冲量特点由动量定理得

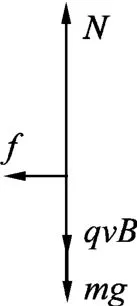
图13