多版本教材比较 促学生深度学习——以“配方法解一元二次方程”为例

李慧芬|浙江省杭州市临平区乔司中学

数学深度学习是指学生在理解性学习的基础上，通过深切的体验与深入的思考，对数学本质进行深度感悟，进而作出决策和解决问题[1].深度学习的发生条件之一是学生思考和操作的对象，必须是经过教师精心设计、具有教学意图的结构化教学材料[2].近年来，大家都很重视对深度学习的研究与实践探索，在深度学习的理论研究、教学策略、教学评价等方面都有很多成果，尤其是在教学策略上积累出不少好的经验，如注重问题设计、开展专题学习、重视文本阅读等，很大程度上转变了教师的教学理念.但在实际备课中，一线普通教师在设计适合学生的有挑战的学习任务与活动方面，仍存在很大困难.下面，笔者从浙教版、北师大版、人教版义务教育教科书《数学》（以下分别简称“浙教版教材”“北师大版教材”“人教版教材”）中“配方法解一元二次方程”的比较入手，探究促进学生深度学习的相关策略，旨在交流与共勉.

一、教学内容比较与策略设计

课程标准是国家课程的纲领性文件，教师在研究教材、进行教学设计时应把其放在首位.《义务教育数学课程标准（2011年版）》（以下简称“《课程标准》”）对配方法的要求是：“理解配方法，能用配方法、公式法、因式分解法解数字系数的一元二次方程.”配方法是开平方的拓展与延伸，其理论依据是完全平方公式，但学生对配方法的掌握有一定困难，教学中应重视促进学生对配方法的理解.

在课时安排上，浙教版教材和北师大版教材都把这部分知识分解成了两个课时：第1课时是用配方法解二次项系数为1的一元二次方程；第2课时是用配方法解二次项系数不为1的一元二次方程.这样编排的目的是降低配方法的难度，呈现知识的螺旋上升.人教版教材则安排了1个课时，在内容的编排逻辑上仍然是螺旋上升的，但对教师的整个教学流程设计和学生的接受能力都提出了更高的要求.

基于对上述三版教材的比较，笔者将教学内容优化为：第1课时，用配方法解二次项系数为1的一元二次方程（既是重点也是难点）；第2课时，用配方法解二次项系数不为1的一元二次方程（在第1课时的基础上，只需把二次项系数化为1，第2课时其实就是第1课时的巩固与提升）.第1课时作为教学重点，目标设置为：能根据平方根的意义解形如（x+m）2=n（n≥0）的方程，能用配方法解二次项系数为1的一元二次方程.

二、导入方式比较与策略设计

用配方法解一元二次方程这一内容的知识生长点是平方根的意义，因此在新课开始阶段，教师要对平方根进行复习.浙教版教材的引入部分采取复习式引入，即“根据平方根的定义，求解形如x2=a（a≥0）的方程的方法叫开平方法”.这种引入方式直截了当，直指这节课研究的核心——x2=a（a≥0）这种类型方程的解法，但直接引入含字母的表达式则比较抽象，不符合学生由简单到复杂、由特殊到一般的认知规律.而人教版教材和北师大版教材处理得相对要好一些，都是以实际例子引入.人教版教材以“油漆刷盒子问题”引入，列出方程x2=25，然后根据平方根的定义求出x1=5，x2=-5，最后根据实际定义得出棱长为5dm.问题虽然简单，但其解答过程是一个用一元二次方程模型解决问题的完整过程.这样的引入关注了学生问题解决的能力.北师大版教材则以上一节课的问题“梯子的低端滑动了多少米”引出课题，注重整个章节的整体联系，根据问题列出方程x2+12x-15=0，但学生要在学习这节课后方能解答该方程.这样的引入能让学生自然产生进一步求解问题的愿望，激起学习兴趣.相较而言，人教版的引入方式更加合适，因为其情境比较简单，且列出的方程就是这节课要研究的配方法类型，这既是引入，又是探究（用配方法来解一元二次方程的第一个探究环节），比较自然.

因此，笔者在实践中选择了人教版教材的引入设计，尽管问题情境比较简单，但学生在解答时经历了用一元二次方程模型解决实际问题的完整过程，这对实现方程大单元目标“体会模型思想”是有必要的.而根据问题列出的简单方程x2=25，可让学生直接想到用开平方法解出方程，这又复习了平方根，为接下来探究新知作好铺垫.这样的引入设计能唤起学生的记忆，明确现在会求的方程特点是x2=p（p≥0）类型，这既是后续知识方程转化的目标，又是探究配方法的基础.

三、探究逻辑比较与策略设计

《课程标准》要求教师注重结合具体的学习内容，设计有效的数学探究活动，使学生经历数学的发生发展过程.这也是学生积累数学活动经验的重要途径.三版教材对配方法的探究逻辑各有特点，具体比较如下.

浙教版教材的探究逻辑顺序是方程形式由简单到复杂，从具体到一般，符合学生的认知规律.在每个环节中，教材语言表达简明扼要，脚手架不多，这既给了教师和学生发挥的空间，又对教师研读教材和教学设计能力提出了高要求.具体如图1所示.

图1 浙教版教材配方法的探究过程

人教版教材的探究逻辑编写非常注重学生的认识发展水平和已有经验，方程类型设计层层递进：x2=25→x2=p（p≥0）→（x+3）2=5→x2+6x+4=0.把对x2=p（p≥0）解的讨论环节放在求x2=25解的环节之后，既是对x2=25类型方程的一般化归纳，又让学生更容易实现化归，并顺利迁移到（x+3）2=5的求解.这样的编排符合学生的认知，便于学生理解.具体如图2所示.

图2 人教版教材配方法的探究过程

北师大版教材与人教版教材的探究逻辑在总体思路上保持一致，但北师大版更注重学生的充分体验和独立思考能力.教材通过“议一议”环节抛出4个不同类型的具体的一元二次方程，让学生充分体验后再提炼出四个方程都可转化为（x+m）2=n（n≥0）的形式.要求探究的这几个方程还暗藏玄机，后一个方程只需变化一步即可得到前一个方程.这样环环相扣的设计，便于学生独立探索，有利于学生从多个事例中观察归纳共同特征，培养化归思想.具体如图3所示.

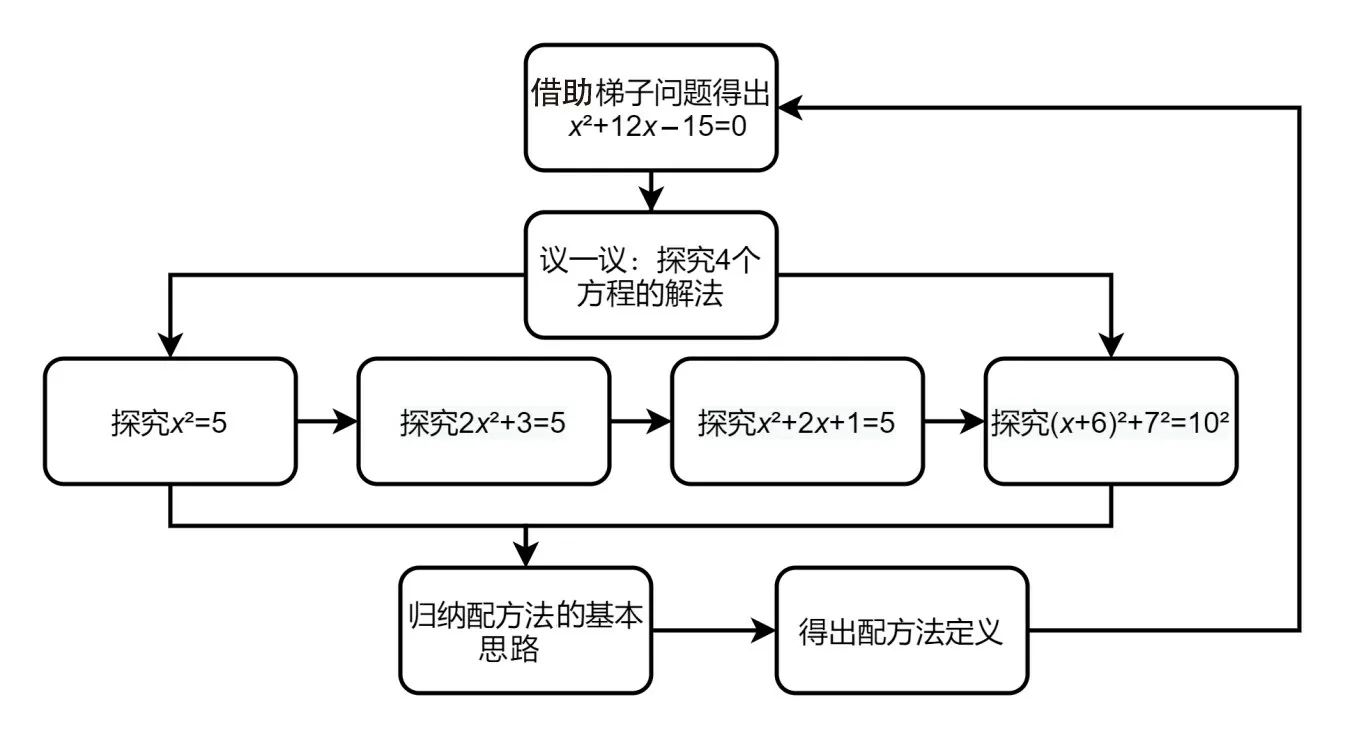
图3 北师大版教材配方法的探究过程

综上所述，三版教材在探究配方法解一元二次方程时，分别选择了“合作学习”“探究”“议一议”等方式，让学生亲身经历配方法的探究过程，都有利于加深学生对配方法的理解，体会化归思想.三版教材的探究都从学生知识的生长点，即平方根的定义出发，从最简单的一元二次方程x2=p（p≥0）开始探究，到（x+m）2=n（n≥0）类型，最后到x2+bx+c=0类型，呈现出了知识的螺旋上升特点.

但是，要在实践中有效设计探究活动，教师还需要结合任教班级的学情，对教材进行重组和再设计，使教学符合学生的认知发展规律.笔者在实践中按照如下三步设计.

第一步：理解x2=p（p≥0）和（x+m）2=p（p≥0）类型的共性，掌握（x+m）2=p（p≥0）类型方程的解法.在前面的引入中，学生已经会根据平方根定义求出x2=25的解，接下来，笔者提出问题：“类比x2=25的解题过程，你能用同样的方法解决下列方程吗？（x-1）2=25；（x-1）2-1=24；x2-2x+1=25.”这三个方程，实质是同一个方程的不同形式，如此并列呈现，有利于学生在自主观察与尝试中不断验证，理解共性，体会整体思想.

第二步：理解配方法就是把方程配成完全平方式的形式加以解决.在学生已经掌握了（x+m）2=p（p≥0）方程的解法之后，笔者再安排挑战性任务：“你能解方程x2+6x+4=0吗？”然后组织学生讨论，通过观察方程的结构与完全平方式的联系找到突破点，领悟解决此类方程可把方程配成完全平方式的形式解决，体会由特殊到一般的数学思想.

第三步：用框图呈现解题全过程，突出配方与降次，发现解一元二次方程的基本思路.实践中，笔者采取人教版教材的框图形式（九年级上册第7页）突出方程x2+6x+4=0的每一步解法，提出问题：“（1）移项后，方程两边为什么加上9？加上其他数字可以吗？（2）通过配方法，方程最后化简为x+3= 5和x+3=- 5两个方程，由此你认为解一元二次方程的基本思想是什么？”以此引导学生进一步掌握配方法的基本步骤，发现解一元二次方程的基本思想就是降次，从而进一步理解配方法.

综上所述，通过比较多版本教材，教师可提高教学设计的有效性，设计出能促进学生深度学习的教学环节.但是，在实践中教师需要注意三个方面的问题：（1）明确课程标准是教学的依据；（2）抓住各版本教材的共性；（3）依据学情设计教学.