基于双种群进化算法的对地观测卫星一体化调度研究

周忠宝，李瑞阳，常中祥*，陈恩铭，刘书源

(1.湖南大学 工商管理学院，湖南 长沙 410082；2.应急管理智能决策技术湖南省重点实验室，湖南 长沙 410082)

0 引言

近年来，我国航天事业快速发展，气象、海洋、陆地资源卫星和商业化遥感卫星在轨数量已稳居世界第二，尤其是近几年发展迅速的商业化遥感卫星在区域治理、灾害监测和评估与救援等方面提供了重要的技术支撑[1]。然而，面对迅速增长的观测需求，有限的对地观测卫星资源仍显得异常宝贵，如何对卫星资源进行统筹规划，在有限的时间内利用更少的资源来完成更多观测需求已经成为卫星管控领域的重要问题[2]。对地观测卫星任务可以分为卫星成像观测和成像数据回传2个阶段，而以往的研究中会优先某一阶段或聚焦单一阶段进行[3]。因此，研究高效、实用的对地观测卫星一体化调度方法对卫星资源的高效利用具有重要意义[4]。

自1996年Bensana等人[5]提出卫星日常管理问题以来，卫星任务规划问题已经得到了广泛且深入的研究[2-6]。2002年，Lematre[7]正式提出敏捷卫星成像规划问题，分析了敏捷成像的特点并从理论上证明敏捷卫星成像规划问题为高度复杂的NP-Hard问题。自此，国内外的大量学者围绕卫星任务规划问题展开了一系列研究，整体可分为3类[3]：第1类为分离式调度，类似于文献[7]的研究，此类研究在任务规划过程中只关注一个阶段，如文献[8-12]只关注成像观测，而文献[13-15]只关注数据回传；第2类为妥协式调度，此类研究在任务规划过程中重点对某一阶段进行优化，并将另一阶段转化为约束条件，在任务规划过程中一定程度上兼顾了2个阶段[16-17]；第3类为一体化调度(亦称综合调度)，即在任务规划过程中综合考虑卫星成像观测和成像数据回放2个阶段[18]，近年来已有部分学者开始聚焦于此类模型的构建及相关算法的设计[19-21]。Chang等人[3]通过多种测试场景下的仿真实验证明了一体化调度在上述3类调度中展现出巨大优势，因此本文在后续研究中也将采取此种调度模式，在问题假设和模型构建中综合考虑2个阶段，从而实现二者协同优化。

卫星任务规划问题作为一种复杂的组合优化问题，无法在多项式时间内求得其最优解，而且在实际应用中往往存在规模庞大、约束复杂和目标不唯一等问题，这导致很难找到适用于所有问题的通用算法[2]。因此，大量学者将研究重点聚焦在卫星任务规划问题求解算法的设计，得益于进化算法简洁且高效的特性，遗传算法[9,13,22]、蚁群算法[8,15,23]和差分进化算法[24-25]等进化算法在卫星任务规划问题的算法设计中得到了广泛的应用[4]。

以上研究虽然已经能够在一定程度上解决卫星任务规划的问题，但是仍然存在约束不全面或求解质量不稳定等问题。因此，本文针对对地观测卫星一体化调度问题，基于存在约束的双种群进化算法(Constrained Dual-Population Evolutionary Algorithm，c-DPEA)，结合启发式规则设计了求解算法，为对地观测卫星资源的高效利用提供了一种高效、可靠的解决方案。

1 对地观测卫星一体化调度问题

对地观测卫星一体化调度问题中包括对地观测卫星、地面站以及观测任务3个对象。每个任务可分为卫星成像观测和成像数据回传2个阶段，分别受到对地观测卫星与观测任务的可见时间窗口限制和对地观测卫星与地面站的可见时间窗口限制。为明晰本文研究问题的重点和边界，做出以下合理假设：

① 本文只考虑点目标，即卫星一次过境可以完整观测的地面目标；

② 由于卫星观测需求远大于卫星观测资源，假设每个目标至多只能被观测一次，且成像数据也至多回传一次；

③ 卫星为“记录—回放”模式，即只有先完成地面目标观测，才可以进行成像数据回放；

④ 成像数据按照“先记录，先回放”的原则进行数据回传，且成像数据不可分割；

⑤ 若观测数据被回传或过期，则其所占据的卫星存储空间被释放；

⑥ 观测成像的数据产生速率和数据回传速率一般成固定比例，在此处为方便计算，假设每个观测任务的成像速率和回传速率相等；

⑦ 同一卫星在同一时刻只能与一个地面站进行数据传输，且受最短工作时间约束；

⑧ 假设卫星一直处于开机状态，不考虑设备故障、特殊工况等问题，不考虑中继卫星。

对地观测卫星一体化调度问题的描述包括元素构成和约束条件，可将其表示为P：

P={St,Et,GT,S,OTW,G,DTW,OT,DT,Cons}，

(1)

式中，[St,Et]为有效调度时间范围，本文假设有效调度时间为24 h；GT={gt1,gt2,…,gtnGT}为地面目标集合，每个地面目标gti具有属性：成像时长di，数据有效期oi，任务优先级ωi；S={s1,s2,…,snS}为对地观测卫星集合，集合中共包含nS=|S|个卫星，每个卫星的最小成像时间均为d0，最大存储空间为Θ；OTWij={otwij1,otwij2,…,otwijn(OTWij)}为卫星sj与地面目标gti的可见窗口集合，otwijk是卫星sj上地面目标gti的第k个可见时间窗口，集合中共包含n(OTWij)=|OTWij|个可见窗口，每个可见窗口具有属性：窗口开始时间ostijk，窗口结束时间oetijk；G={g1,g2,…,gn(G)}为地面站集合，集合中共包含n(G)=|G|个地面站，每一个地面站的最短工作时间为d0；DTWlj={dtwlj1,dtwlj2,…,dtwljn(DTWlj)}为卫星sj与地面站gl的可见窗口集合(亦称传输窗口)，dtwljq是卫星sj与地面站gl的第q个可见时间窗口，集合包括n(DTWlj)=|DTWlj|个可见目标，每个可见窗口具有属性：窗口开始时间dstljq，窗口结束时间detljq；OT={ot1,ot2,…,otn(OT)}为有效调度时间范围内，调度形成的观测成像任务集合，包括n(OT)=|OT|个任务，每个观测任务oti具有属性：观测目标gti，执行观测任务的卫星si，观测任务开始时间ost′ijk，观测任务结束时间oet′ijk；DT={dt1,dt2,…,dtn(DT)}为有效调度时间范围内，调度形成的数据回传任务集合，集合包括n(DT)=|DT|个任务，每个数传任务dtv(其中v=ljq)具有属性：数传任务对应的观测任务集合dSetv，执行数传任务的卫星sv，数传任务开始时间dst′ljq，数传任务结束时间det′ljq；Cons为对地观测卫星一体化调度问题中所包含的所有约束条件，下面将对此部分内容进行详细阐述。

2 对地观测卫星一体化调度模型

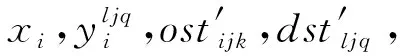
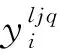
在对地观测卫星一体化调度问题中，综合考虑观测和数传2个环节，因此对一个地面目标只有完成观测成像并在有效期内完成成像数据回传才可称为一次成功的对地观测，所以考虑Chang等人[3]提出的最小数据获取失败率f1(P)作为本模型的第一个优化目标：

(2)

同样需要考虑如何在任务执行过程中尽量使用较少的能源消耗。因此本模型的第2个优化目标为能源消耗率f2(P)，即观测和数传任务所使用的能源消耗占最大能源消耗的比例为：

(3)

式中，TEC为卫星消耗的能源综合；MEC为执行所有观测任务并用尽所有传输窗口所能产生的最大能源消耗。TEC的计算方法如下：

TEC=(nOT×eo+od×ro)+(nDT×ed+td×rd)+ct×rc+rt×rr，

(4)

式中，eo为观测任务启动能耗；od为全体观测任务的执行总时长；ro为观测成像耗能功率；ed为数传任务启动能耗；td为全体数传任务的传输总时长；rd为数据回传耗能功率；ct和rt分别为姿态机动和天线校对的总时长；rc和rr分别为姿态机动功率和天线校对功率。类似的，可以计算得到MEC：

MEC=nGT×(eo+ro×max(di))+

nDTW×(ed+rd×max(detljq-dstljq))+rc×nGT×ρ+rr×nDTW×σ。

(5)

综合以上，可以得到对地观测卫星一体化调度模型：

min{f1(P),f1(P)}，

(6)

s.t.

xi≤1，

(7)

ostijk·xi≤ost′ijk·xi≤oet′ijk·xi≤oetijk·xi，

(8)

(9)

(ost′i2jk2-oet′i1jk1)·OTAi1i2≥ρ·OTAi1i2，

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(dst′lj2q2-det′lj1q1)·DTAv1v2≥σ·DTAv1v2，

(17)

(18)

xi∈{0,1}。

(19)

本文综合考虑卫星成像观测和数据回传2个阶段的工作，因此模型中需要兼顾2个阶段中的各类约束[3]，数学模型中各公式含义如下：

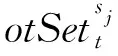
3 基于双种群进化算法的卫星一体化调度算法设计与实现

卫星一体化调度问题是一类典型的约束多目标优化问题(Constrained Multiobjective Optimization Problems，CMOPs)，具有变量类型复杂、强约束和多目标等求解难点。近年来，协同进化算法的出现为解决此类复杂优化问题提供了新的方向[26]。进化算法在解决无约束多目标优化问题(Multi-objective Optimization Problems，MOPs)时已经显现出巨大的优势，然而CMOPs由于约束条件的存在求解时往往具有更大的挑战[27]。Ming等人[28]针对存在约束的多目标优化问题提出了一种基于双种群的协同进化算法c-DPEA，该算法通过2个种群的互补和协作，实现了算法在求解CMOPs的过程中对收敛性和多样性的兼顾。2个种群在处理不可行解时分别采取不同的方案，其中种群1为多样性导向，注重解的目标值优化，保留种群中拥有良好目标值不可行解，保证最终解的多样性；而种群2则以可行性为导向，优先保留可行解，追求更快的收敛速度。2个种群相互补充并在生成子代的过程中进行信息交换，从而实现兼顾收敛性、多样性和可行性的高效进化。

3.1 基于排序的双种群适应度分配

Ming等人[28]在c-DPEA算法中提出了一种基于排序的自适应适应度分配方法bCAD，适应度计算函数形式如下，

(20)

(21)

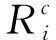
3.2 基于贪婪策略的种群初始化

由于卫星一体化调度问题的复杂性，直接应用进化算法无法在短时间内获得优质解。通过启发式规则形成较好的初始种群势必有利于子代种群在优化迭代的过程中快速向真实前沿靠拢，因此本文也在种群初始化过程中采用了一类受到广泛使用的贪婪策略。具体流程如下：

① 随机生成观测任务开始时刻，并将观测任务序列中的所有任务初始化为“执行”；

② 首先对每颗卫星的所有观测任务按照优先级由高到低排序；

③ 按照顺序对观测任务依次执行时间窗口约束检查，如果不满足，则将对应任务删除，并对下一个观测任务执行时间窗口约束检查，否则对观测任务执行④；

④ 对当前观测任务的前、后相邻任务执行时间冲突检查，如存在时间冲突则删除较低优先级的观测任务；

⑤ 按照“先观测，先回传”的原则生成数传任务序列和数传任务开始时间；

⑥ 再次进行约束检查，删除无法在有效期内回传的观测任务，得到初始解。

3.3 遗传算子设计

由于本文中包含整数变量和实数变量2类变量，此处引入2类交叉算子和2类变异算子。交叉算子和变异算子均在一定概率下执行。

交叉算子：针对整数变量，使用2点交叉算子，随机选择交配池中的2个个体，在观测任务序列片段或数传任务序列片段中随机选择2个交叉点，交换两交叉点间的片段，即完成交叉操作。针对实数变量，使用模拟二进制交叉(Simulated Binary Crossover，SBX)。

变异算子：针对整数变量，按照一定的变异概率对种群中的个体执行变异操作，即选中一个个体后，随机选择一个变异位，改变变异位原始值，即将0改为1或将1改为0。针对实数变量，采用多项式变异。

3.4 种群更新

在每一代结束时，将种群1和种群2中的个体合并为一个种群规模为2N的组合种群，然后通过二元锦标赛从组合种群中选择个体进入交配池。首先对组合种群基于bCAD进行排名，然后从组合种群中随机选出的2个解，选择bCAD分配排名更好的一个进入交配池，在形成规模为2N的交配池后，通过引入交叉算子和变异算子产生种群规模为N的后代种群。

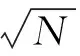
(22)

其中，

(23)

(24)

式中，γ为2个种群中相同解占种群规模的比例。

种群2则是通过将所有的不可行解投影至Fmax，Fmax为整个种群在各目标维度的最大值所组成的负理想点，修正如式(25)所示，其中wf为Fmax所属的单位向量。种群2通过对不可行解的修正，在种群更新过程中尽快实现对不可行解的淘汰，从而实现可行性导向的种群进化，即：

(25)

2个种群差异化的更新方式结合bCAD自适应适应度分配方法，最终使得本算法能够实现在广泛搜索的同时兼顾快速收敛，使得求解质量和求解效率均得到保证。

3.5 操作算子设计

作为一种混合整数规划问题，直接使用进化算法求解卫星一体化调度问题往往很难得到较好的结果。随着启发式规则的引入，通过一些操作算子对种群个体的任务序列进行破坏和修复，能够极大地改善算法的寻优效率[29]。为此，本文引入4类破坏算子和对应的4类修复算子，具体情况如下。

(1) 破坏算子

① 优先级准则破坏算子，按照优先级从低到高对所有已调度任务进行排序，并按照次序删除任务，即优先删除低优先级任务，并将对应任务存入禁忌池。

② 能耗准则破坏算子，按照能耗从高到低对所有已调度任务进行排序，并按照次序删除任务，即优先删除高能耗任务，并将对应任务存入禁忌池。

③ 随机准则破坏算子，将所有已调度任务随机排序，并按照次序删除任务，并将对应任务存入禁忌池。

④ 拥堵度准则破坏算子，按照拥堵度(每个观测任务时间窗口与其他观测任务时间窗口发生冲突的次数)由高到低将所有已调度任务排序，然后按照次序删除任务，并将对应任务存入禁忌池。

(2) 修复算子

① 优先级准则修复算子，按照优先级从高到低对所有未调度且不在禁忌池内的任务进行排序，并按照次序依次尝试插入任务，即优先插入高优先级任务。

② 能耗准则修复算子，按照能耗从低到高对所有未调度且不在禁忌池内的任务排序，然后按照次序依次尝试插入任务，即优先插入低能耗任务。

③ 随机准则修复算子，将所有未调度且不在禁忌池内的任务排序，然后按照次序依次尝试插入任务。

④ 拥堵度准则修复算子，按照拥堵度由低到高将所有未调度且不在禁忌池内的任务排序，然后按照次序依次尝试插入任务。

本算法在每次迭代产生子代后，随机选取一部分子代执行约束检查，然后进行任务删除和任务插入操作。将生成的新子代重新放回全部子代，通过环境选择进入后续种群。

3.6 算法实现

本研究算法步骤如下：

① 设置种群规模、最大迭代次数和插入概率等参数；

② 基于贪婪规则产生初始种群，并对种群中每个个体进行混合整数编码；

③ 对个体进行冲突检查和处理，然后复制得到种群1和种群2；

④ 判断是否达到最大迭代次数，如果达到最大迭代次数则输出种群2，否则执行⑤；

⑤ 通过锦标赛选择产生交配池；

⑥ 通过交叉、变异得到子代种群，并随机对子代种群执行冲突检查和任务插入；

⑦ 通过种群1和种群2的环境选择，更新种群1和种群2，然后执行④。

算法流程如图1所示。

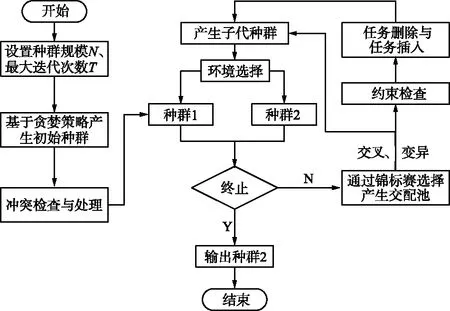
图1 算法流程Fig.1 Algorithm flow

4 算例与分析

为了验证基于双种群进化算法对卫星一体化调度问题求解的收敛速度，采用Chang等人提出的基于现实的模拟实例生成方法产生模拟数据建立仿真算例，模拟数据产生过程中设定如下：

① 对地观测卫星：设定卫星数量为10颗，分别为“高分”系列卫星(GF0101，GF0201，GF0601)、“高景”系列卫星(SV01，SV02，SV03，SV04)以及资源系列卫星(ZY02C，ZY3，ZY0104)；

② 地面站：设定为4个，密云站(40°N/117°E)、喀什站(39°N/76°E)、三亚站(18°N/109°E)和挪威站(67°N/21°E)；

③ 地面目标：设定为中国境内随机产生的100个地面目标，所有地面目标的中心点均匀分布于我国大陆范围内(3°～53°N以及74°～133°E)，地面目标的优先级服从均匀分布[1,10]，需求成像时长服从均匀分布[5,20]，单位s，数据有效期计算方式参照文献[3]。

其他参数设定为：观测任务启动能耗eo=500 J，观测成像耗能功率ro=50 W，数传任务启动能耗ed=500 J，数据回传耗能功率rd=80 W。姿态机动功率和天线校对功率rc和rr均为100 W。姿态机动时间ρ设定为100 s，天线校对时间σ设定为100 s。

算法的主要参数设定为：种群规模100，最大迭代次数100，交叉概率为0.9，变异概率为0.1，4类破坏操作算子和4类修复操作算子的选择概率均为0.25，插入概率(选择执行约束检查和任务删除与插入的概率)为0.5。

经过30次运行加入贪婪策略的c-DPEA卫星一体化调度算法，得到运行结果如表1所示。

表1 算法运行整体情况Tab.1 Description of algorithm operation

经过多次实验发现，不同的任务插入概率下操作算子对最优解和收敛速度均产生不同的影响，这里采用多目标优化评价指标超体积(Hypervolume，HV)对不同任务插入概率下的进化过程进行分析[30]。

此处以0.1为间隔选取[0,1]内的11个值为插入概率，并设置最大迭代次数为100时得到各个个体的超体积，如图2所示。在以上各个情况下分别得到最终代帕累托前沿，如图3所示，横纵坐标分别为目标函数值，目标函数已经做了无量纲化的处理。

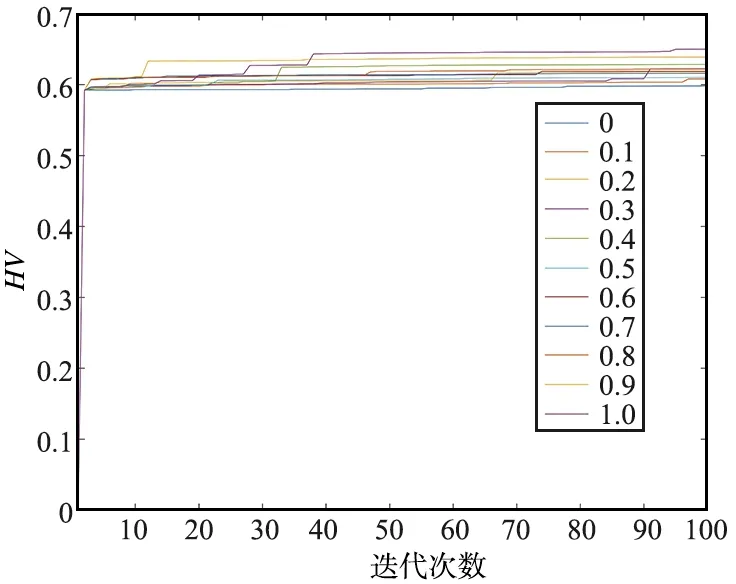
图2 不同插入概率下的HVFig.2 HV with different insert rates

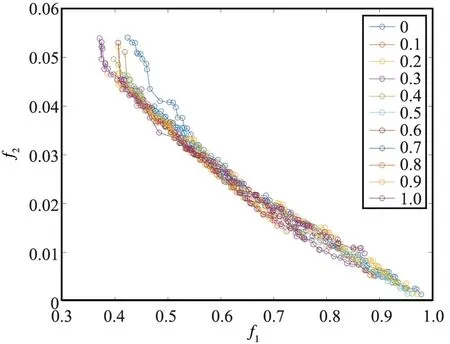
图3 不同插入概率下的收敛分布Fig.3 Convergence distribution with different insert rates

不难发现，随着插入概率的增大，种群将能够搜索到更优的前沿，但与此同时算法的收敛速度也随之下降，因此在实际问题中可以根据精度需求设置合理的插入概率，从而实现求解质量和求解速度的兼顾。

在求解质量方面，本文选取Chang等人[3]提出的ALNS+NSGA-II算法作为比较对象，分别选取100地面目标、200地面目标、300地面目标和500地面目标4种测试场景对算法进行测验，每个算法都以相同的初始解进行迭代寻优，得到最终的帕累托前沿，如图4所示，各子图横纵坐标为目标1和目标2的函数值。可以看到，基于贪婪策略的c-DPEA算法在各个场景下均可以获得更为宽广的帕累托前沿，即算法可以更为广泛地搜索整个空间，求得更具多样性的解。由于最大迭代次数的限制，c-DPEA算法所获得的部分前沿劣于ALNS+NSGA-II，然而通过设置更大的最大迭代次数，即通过牺牲一定的求解速度，可以进一步获得更为优秀的帕累托前沿，从而实现解的进一步优化，如图5所示。

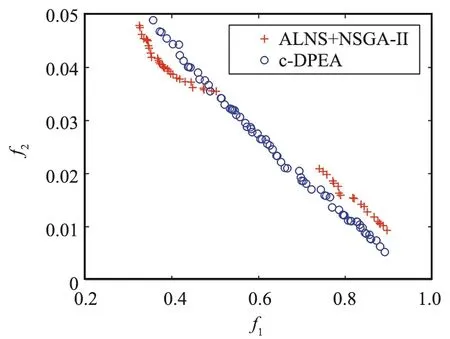
(a) 100 targets

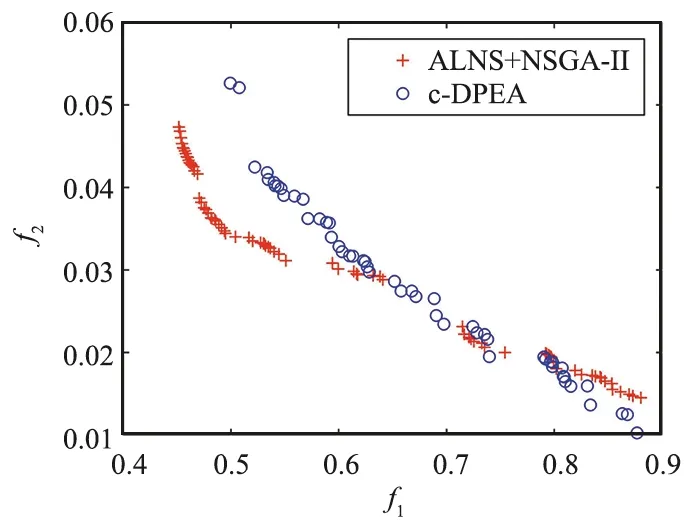
(b) 200 targets

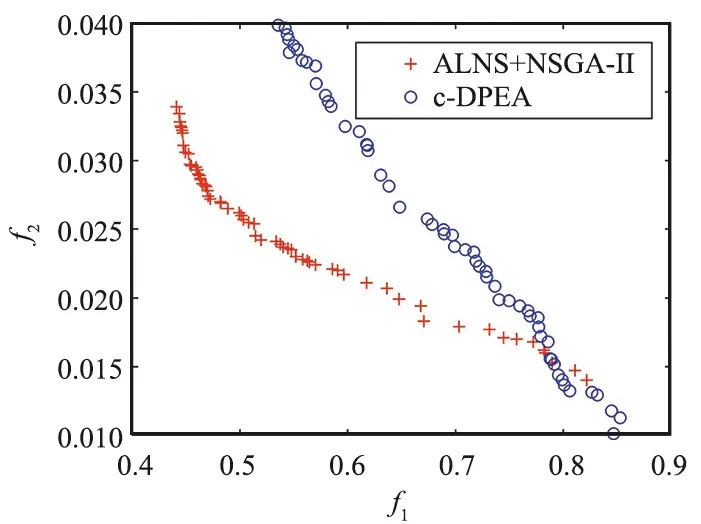
(c) 300 targets

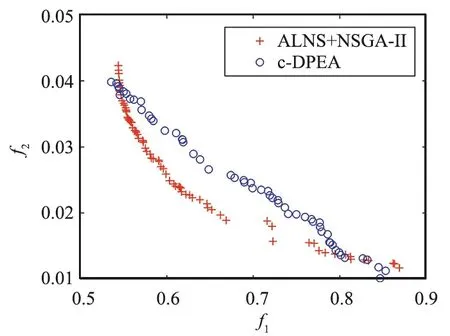
(d) 500 targets图4 c-DPEA和ALNS+NSGA-II的收敛分布Fig.4 Convergence distribution of c-DPEA and ALNS+NSGA-II

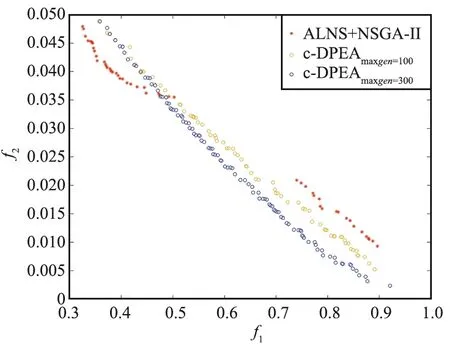
图5 不同最大迭代次数下的c-DPEA帕累托前沿Fig.5 Pareto front of c-DPEA with different maximum iterations

5 结束语

针对一类同时关注对观测成像任务和成像数据回传任务的对地观测卫星一体化调度问题进行了分析和建模。基于现实应用场景构建了对地观测卫星一体化调度模型，并设计了与之对应的混合整数规划模型。通过对模型中约束条件和问题特性进行分析，设计了一种基于贪婪策略的初始解生成方法，在c-DPEA算法中引入操作算子设计了针对卫星一体化调度问题的贪婪双种群进化算法。该方法通过双种群的互补和协作，兼顾了卫星一体化调度问题求解过程中的求解多样性和收敛速度。

本文仍存在一些不足，算法中将操作算子的权重设为恒定值，可以通过引入自适应的权重更新方法帮助子代个体在解空间内更为快速、广泛地探索，从而进一步提高算法求解质量和收敛速度，实现算法效率的进一步提升。此外，本文只考虑了4类操作算子，未来还可以引入更多类型的操作算子来进一步提高算法对卫星一体化调度的求解能力。