基于预设性能神经网络的智能鲁棒交会任务规划
2022-06-29何文志李思男
靳 锴,何文志,宗 茂,李思男
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.河北省无人系统智能测控信息技术重点实验室,河北 石家庄 050081)
0 引言
空间交会任务规划是航天器完成空间在轨服务的基础,包括对卫星进行在轨装配、故障维修、燃料加注、模块更换、技术升级以及辅助机构展开等。其中,航天器在轨服务与维护的对象主要包括失效卫星、失控航天器和空间垃圾等空间非合作目标,由于空间非合作目标在信息层面上不沟通、机动行为上不配合,导致非合作目标的交会轨迹规划与合作目标不同,需要对任务中的不确定因素进行辨识与处理。文献[1]通过对370篇相关学术论文的研究,梳理和总结了航天器服务有关技术发展的前沿性和待解决的问题,并明确指出:过去的20年里已成功实现了许多在轨服务任务,但是大多是针对合作性目标,而对非合作目标的在轨操作仍是一个具有多种技术挑战的研究领域,尤其是在考虑不确定因素下的智能鲁棒交会任务规划问题亟待解决。
传统的交会任务规划将相对运动模型视为确定性系统,不考虑其中存在的不确定性因素,通过优化方法得到最优交会任务。而在实际的交会过程中,存在包括导航制导与控制不确定性、环境不确定性、未建模动态以及参数不确定性等因素,导致交会精度无法保证。针对不确定性问题,专家学者们开展了大量研究,文献[2]梳理了深度不确定环境下决策分析的研究现状,总结了问题的特征和难点,分类阐述了主要方法的起源与发展、核心思想、实现步骤和典型应用。文献[3-4]采用蒙特卡洛方法,在不同坐标系下对高斯分布的不确定性传播进行分析。文献[5]研究了线性协方差(Linear Covariance,LinCov)理论用以分析导航误差对轨迹偏差的影响。文献[6-7]采用统计线性化(Statistical Linearization,SL)的方式对导弹的碰撞概率进行了分析,这种方法要求概率密度函数已知且非线性较弱。文献[8-9]提出了状态转移张量(State Transition Tensors, STTs)方法,通过初始不确定性的解析映射求解局部非线性的高阶泰勒展开,从而得到不确定性的预测模型。文献[10]采用多项式混沌(Polynomial Chaos,PC)方法,对随机微分方程的解进行逼近,从而实现对不确定性的描述。文献[11-12]采用高斯混合模型(Gaussian Mixture Model,GMM)方法,分别对考虑太阳光压影响下的轨道确定问题以及气动阻力对不确定性传播的影响进行了分析。文献[13-14]研究了一种基于微分代数理(Differential Algebra,DA)建立非线性不确定预测模型的方法,该方法能够避免复杂的偏微分计算与数值逼近。文献[15]总结了现有的线性与非线性系统不确定性预测方法,对各种方法进行全面综述,将不确定性传播方法分类。文献[16-18]采用协同进化与自适应方法,对卫星轨道部署与路径规划进行了研究,所提出方法在恶劣通信环境下有效。以上研究仅是对已知的不确定因素进行了预测,而没有对不确定因素进行辨识与处理。
本文面向空间非合作目标在轨服务的特点和需求,综合考虑空间非合作目标在信息层面上不沟通、机动行为上不配合、观测受限以及不确定性因素影响,研究了一种基于长短时记忆(Long-Short Term Memory,LSTM)与预设性能控制(Prescribed Performance Control,PPC)的交会任务规划方法,实现智能自主、安全可靠的航天器交会任务,通过仿真验证了方法的有效性。
1 航天器交会任务描述
在地心惯性坐标系中,服务航天器和目标航天器轨道动力学方程为:
(1)
(2)
(3)
(4)
式中,r为航天器位置矢量;v为航天器速度矢量;μ为地球引力参数;f为作用于航天器上的除推进力与中力引力以外的其他全部力带来的加速度;F为服务航天器上的控制力;m为航天器质量;下标c表示服务航天器;下标t表示目标航天器。
联立式(1)~式(4),可以得到服务航天器与目标航天器相对运动动力学方程在惯性坐标系中的表达式:
(5)
式中,p为相对位置矢量。将上述方程转换到目标航天器轨道坐标系中,重力场一阶近似,并转换为标量形式,可得到:
(6)
(7)
(8)
式中,θ为真近点角;[px,py,pz]T为相对位置矢量在LVLH坐标系下的投影;fx,fy,fz为服务航天器的控制输入。假设航天器运行于近圆轨道,此时式(6)~式(8)可以转化为:
(9)
(10)
(11)
式中,nt为目标航天器轨道角速度。
2 LSTM-PPC交会任务规划
2.1 预设性能控制
PPC方法最早由希腊数学者提出,该方法的核心思想是对受控系统的状态误差预先设计边界包络,通过性能包络的收敛特性来描述受控系统的瞬态响应与稳态性能,然后基于边界包络设计控制器。PPC包含3个步骤:首先,针对控制对象的系统状态误差设计性能约束函数;然后,引入对等映射函数将有约束空间同胚映射到无约束空间;最后,在映射得到的新空间内设计控制器,实现预设性能的控制。预设性能原理如图1所示。
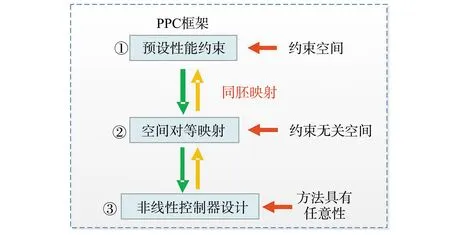
图1 预设性能原理Fig.1 Principle diagram of prescribed performance
考虑多输入多输出(Multiple-Input Multiple-Output,MIMO)系统形式,将式(9)~式(11)表示为简化形式:
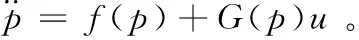
(12)
PPC的核心思想是对受控系统的状态误差预先设计边界包络,通过性能包络的收敛特性来塑造受控系统的瞬态响应与稳态性能。
定义:一个光滑函数,ρ:R+→R+,如果该函数满足:
①ρ(t)为始终为正值的减函数;
② limt→∞ρ(t)=ρ∞>0,
则认为函数ρ(t)为PPC的一个性能函数。
这种性能函数并不唯一,而是具有多种形式。本文采用如下形式的性能函数:
ρ(t)=(ρ0-ρ∞)exp(-lt)+ρ∞,
(13)
式中,ρ0,ρ∞,l均为正实数,ρ0,ρ∞分别为初始时刻与稳定时刻的最大允许误差值,l为设计参数,决定控制系统收敛速度。该形式的ρ(t)满足PPC性能函数定义。
为考虑超调量问题,利用预设性能函数,对性能函数进行如下约束:
(14)
式中,δi为常实数,满足0≤δi≤1。在初始时刻,0<|ei(t)|<ρi(0)。引入常值δi,可以在误差接近零时,不会出现较大的超调量,始终小于δiρi(0)。因此通过调节ρi(t)与δi,可以决定系统边界误差。
2.2 LSTM不确定因素辨识
在工程实际中,由于不确定因素与航天器突发故障,如执行机构、太阳能帆板故障等,难以对模型进行精确建模,模型不确定性严重影响着控制的精度。虽然静态PPC控制结构简单,无需对控制系统的动力学模型进行准确获取,但是其对于动力学模型不确定性的鲁棒性和自适应性具有一定的局限性。因此,为了控制的鲁棒性和自适应性,基于模型性的控制律是首选。因此,采用LSTM实现不确定因素辨识。
LSTM是一种改进的循环神经网络,通过设计合理的输入门、遗忘门(Forget Gate)和输出门(Input Gate),并通过记忆单元(Memory Cell)对状态信息进行记忆来逼近非线性动力学,将原有的短时记忆提高为长时间的记忆,从而能够更好地利用时序信息,对微分方程描述的动力学系统具有更好的拟合效果。LSTM单元结构如图2所示。
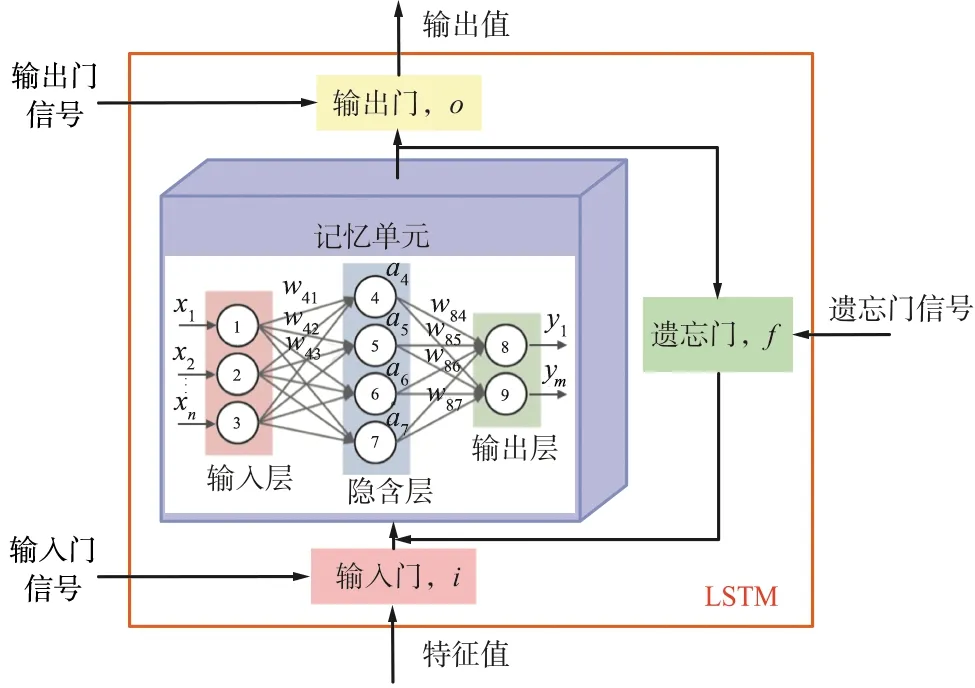
图2 LSTM单元结构Fig.2 LSTM unit structure
LSTM有4个输入和1个输出:第1个输入是普通的特征值输入;第2个输入控制输入信号门是否打开;第3个输入控制遗忘门是否打开;第4个输入控制输出门是否打开;输出为普通输出。
记忆单元为1个前馈神经网络。主要分为3层:第1层为输入层;第2层为隐含层;第3层为输出层。各层神经元接收上一层的输出,并经过激励函数输出到下一层。LSTM 的一个特点是数据学习的循环型,在每一循环中,神经元接收输入和前一步的输出,作为本次循环的输入。
根据LSTM原理,在交会任务不确定因素模型辨识的过程中,构建如图3所示的LSTM控制流程,补偿不确定因素与应对执行机构故障的影响。
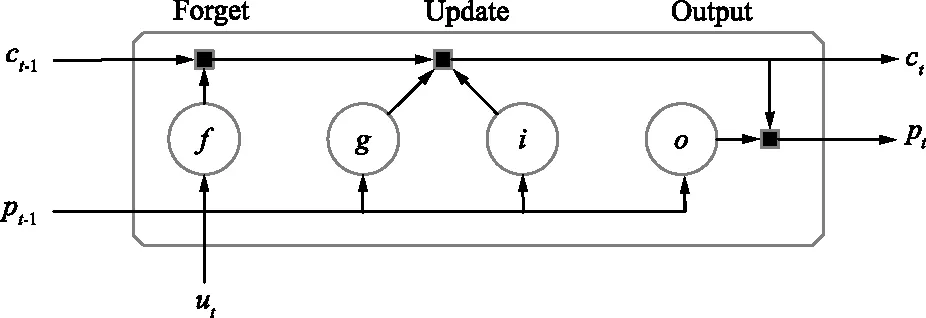
图3 LSTM示意Fig.3 LSTM schematic diagram
输入信号ut为航天器t时刻任务指令,输出信号pt为航天器相对状态,输入门控制信号为it,输出门控制信号为ot,遗忘门控制信号为ft,隐含层控制信号为gt,h(·)为sigmoid激励函数。
根据图3,输出状态、记忆状态可以表示为:
pt=ot×h(ct),
(15)
ct=ft×ct-1+it×gt,
(16)
式中,
it=h(Wiut+Nipt-1),
(17)
ft=h(Wfut+Nfpt-1),
(18)
gt=h(Wgut+Ngpt-1),
(19)
ot=h(Wout+Nopt-1),
(20)
(21)
学习矩阵包括输入权重W和循环权重N,可表示为:
W=[Wi,Wf,Wg,Wo]T∈R4n×(m+1),
(22)
N=[Ni,Nf,Ng,No]T∈N4n×n,
(23)
式中,n,m分别为神经网络中隐含单元个数与输入变量长度。学习矩阵的数据样本可在航天器在轨运行过程中获取。
2.3 最终逼近段控制器设计
利用上文所述理论对非合作目标交会最终逼近段进行控制器设计,设计基于LSTM-PPC的任务规划原理如图4所示。
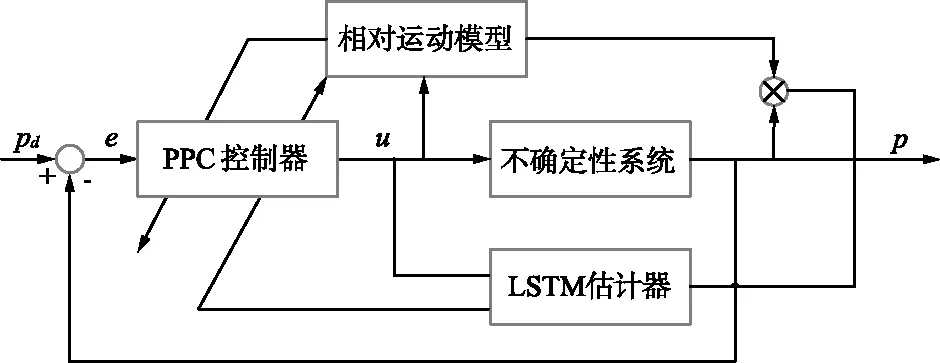
图4 LSTM-PPC 的任务规划原理Fig.4 LSTM-PPC mission planning principle diagram
根据PPC控制方法,依据式(14)与交会任务,定义如下严格递减的正值预设性能函数:
ρ(t)=(e0-ereq)exp(-lt)+ereq,
(24)
式中,l为由交会任务收敛速度要求与执行机构性能共同决定的正常数;e0为交会任务的初始误差;ereq为任务的精度需求。
为了方便考虑超调量与无约束转化问题,设计误差映射函数:
S()
(25)
针对相对动力学模型,定义如下所示的误差矩阵:
E(t)=r+λv,
(26)
式中,常值矩阵λ=diag(λ1,λ2,λ3)为设计值。
设计控制率为:
u=ua-sign(G)(ηa|ua|+ηb|ub|)RTE,
(27)
(28)
(29)
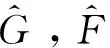
3 仿真验证
为了验证方法的有效性,对包含不确定因素的航天器交会任务规划进行仿真验证。目标航天器轨道参数为高度h=400 km ,轨道倾角i=0.52 rad,偏心率e=0。目标航天器面质比为A/m=0.02 m2/kg,大气密度ρ=1.23e1.38×10-4h,阻力系数Cd=1,扰动加速度与执行机构故障参数如表1所示。

表1 扰动加速度与执行机构故障参数Tab.1 Disturbance acceleration and actuator failure parameters
交会任务为初始相对状态x0=(20 m,-200 m,-20 m,0 m/s,0 m/s,0 m/s),期望末端相对状态xf=(0 m,0 m,0 m,0 m/s,0 m/s,0 m/s),任务时间tf=200 s。
设计包含4层隐含层单元的LSTM,利用反向传播法得到LSTM参数用以描述不确定因素与执行机构误差补偿。设计任务参数e0=200,ereq=10-3,l=0.025,λ=diag(12,35,12),k=30,δD=0.1,nf=0.25,ηa=0.25,ηb=0.25。
仿真结果如图5~图7所示。由图5(a)可以看出,采用本文方法在不确定因素以及执行机构故障的情况下,服务航天器的运动状态仍然能够在预设的性能约束内沿对接轴高精度地接近目标航天器,完成交会任务。地心方向、切向和法向的误差均能按照预设瞬态性能在200 s时趋近于零,使服务航天器沿对接轴高精度、平稳接近目标航天器。由图5(b)可以看出,传统PID方法没有考虑性能约束,在瞬态上收敛过程无法以给定误差范围收敛,且未进行不确定性因素辨识,最终收敛精度上有较大误差(米级),控制性能无法满足任务要求。由图6(a)中的任务控制指令曲线可以看出,本文方法整个逼近过程中执行机构控制平滑,控制加速度始终小于0.1 m/s2,满足约束条件。由图6(b)可以看出,传统PID方法给出的任务控制指令相对较大,且难以快速稳定,增加了任务的燃料消耗。由图7可以看出,本文方法交会轨迹能沿对接走廊高精度到达终点,而传统PID方法交会轨迹精度较差。
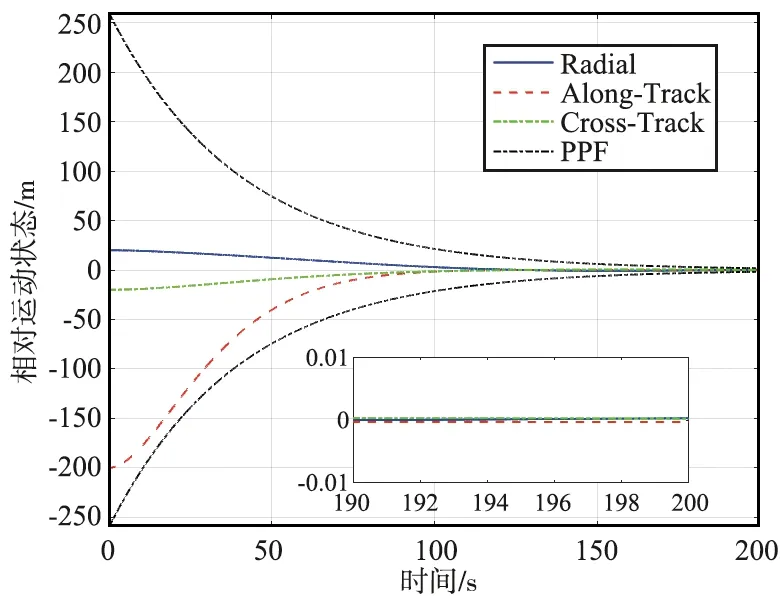
(a) 本文方法
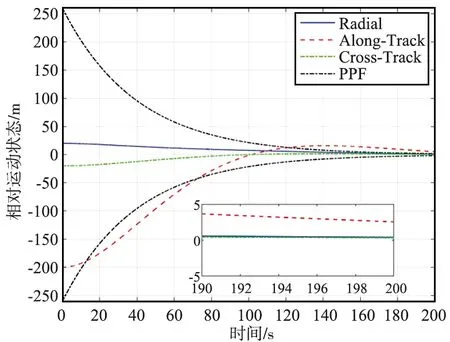
(b) PID控制方法图5 预设性能包络下相对运动状态Fig.5 Relative motion state enveloped under LSTM-PPC
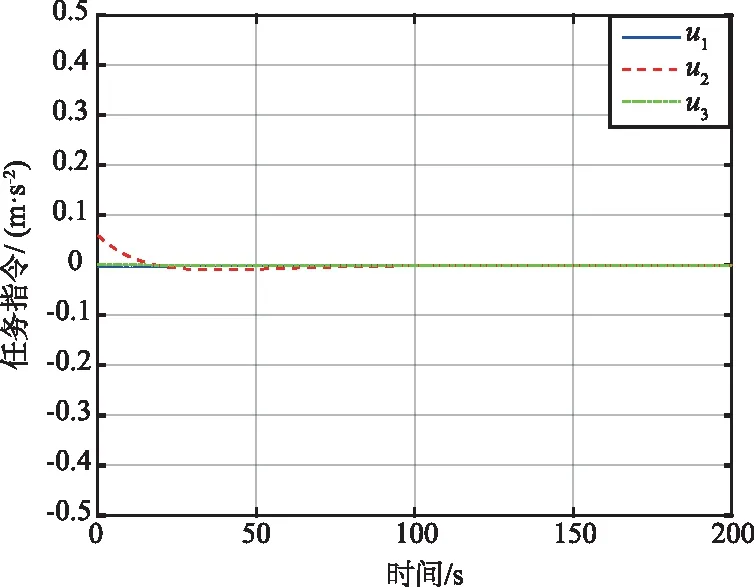
(a) 本文方法
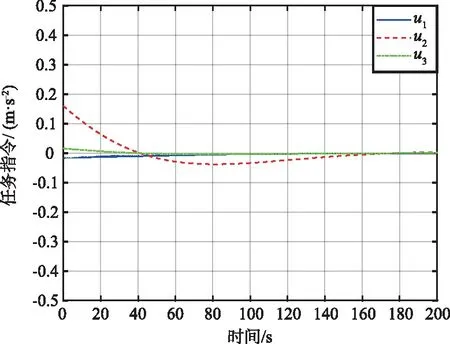
(b) PID控制方法图6 任务指令Fig.6 Mission instructions
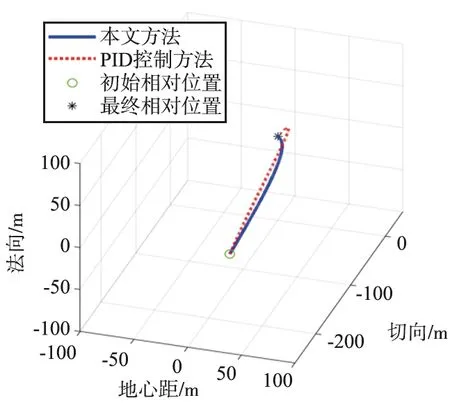
图7 交会任务轨迹Fig.7 Rendezvous mission trajectory
4 结束语
本文针对存在不确定因素的空间非合作目标交会任务规划问题,研究了一种基于LSTM与PPC的智能鲁棒任务规划方法。该方法能够通过LSTM对不确定因素进行辨识,同时利用PPC对航天器的交会任务中的轨迹进行瞬态与稳态性能的设计,能够有效地抑制不确定因素影响,提高航天器交会精度。通过与典型的控制方法进行数值仿真对比可以得出:针对非合作目标这种存在强不确定性、强干扰和未知机动等特点的特殊对象,传统PID方法虽然具有较强的稳定性,但其任务规划性能很差,无法保证追踪航天器的安全和精度;本文提出的LSTM-PPC方法不仅能够对系统信息和不确定性在线辨识,还能够保证系统状态满足实际工程预设的性能范围,具有较强的理论意义和工程应用价值。
