基于多维极限状态函数的桥梁地震易损性分析

唐径遥

(中国铁路广州局集团有限公司长沙高铁工务段 长沙市 410000)

0 引言

桥梁是由多个类型的构件组成的复杂体系，地震作用下，桥梁结构中不同类型构件之间的相互作用，会对桥梁系统的破坏状态产生影响[1]。因此，很有必要对桥梁结构的地震易损性进行深入研究。

地震易损性是指桥梁在地震作用下，发生某一水平破坏的可能性[2]。梁岩等[3]考虑了地震动与损伤指标的不确定性，对地震易损性损伤指标的计算方法进行了研究。单德山等[4]考虑了地震动输入角，分析了某一连续刚构桥构件的地震易损性，并基于一阶界限估计法分析了桥梁系统地震易损性，为评估高墩薄壁桥梁的抗震性能提供了依据。Yan Liang等[5]构造了160个主余震序列，利用一阶界限估计法和二阶界限估计法分析了主余震序列对桥梁系统地震易损性的影响。

目前，为了简化分析，一般用桥梁构件的易损性曲线来代替桥梁系统的易损性曲线，并未考虑桥梁构件之间可能存在的相关性对桥梁系统的影响，使得桥梁系统的地震易损性分析偏高或偏低，从而影响抗震性能的评估。基于上述研究不足，以某一连续刚构桥为研究对象，基于多维极限状态函数进行地震易损性分析，并得到相关结论。

1 地震易损性分析方法

根据定义，地震易损性可表示为：

Pf=P(D>C|IM)

(1)

式中：Pf表示结构的破坏概率；D和C分别表示结构的响应值和抗震能力值；IM表示地震动强度。

1.1 传统的地震易损性分析方法

(1)构件易损性

构件易损性分析中，结构的地震响应中位值与IM之间的关系为指数形式：

(2)

式中：a与b均为拟合参数。

对数正态空间下可将式(2)转化为线性形式：

(3)

则地震易损性可表达为式(4)：

(4)

(2)系统易损性

基于可靠度理论的分析方法，采用一阶界限估计法[6]计算桥梁系统的地震易损性，具体计算见式(5)。

(5)

式中：Pfi表示第i个桥梁构件的破坏概率；Pf表示桥梁系统的破坏概率。

1.2 基于多维极限状态函数的地震易损性分析方法

(1)基于可靠度理论的多维极限状态函数

多维极限状态是指结构的各个构件联合极限破坏状态。根据可靠性理论中极限状态的定义，建立多维极限状态的广义方程[7]。如下：

G(Y,IM)=1-∑(Yi)Ni=0

(6)

式中：G(Y,IM)表示结构的功能函数；Yi表示结构构件的需求能力比；Ni反映不同构件之间的相关性。

连续梁桥的上部结构在地震力作用下通常处于弹性状态，因此只考虑易损构件支座和桥墩之间可能存在的相关性建立如下四种极限状态函数：

①支座和桥墩两构件存在线性关系，根据式(6)得线性极限状态函数：

G(Y,IM)=1-(Y1+Y2)

(7)

式中：Y1表示支座的需求能力比；Y2表示桥墩的需求能力比。

②支座和桥墩两构件存在非线性关系，则根据式(6)可得圆形极限状态函数：

(8)

③支座和桥墩两构件完全相关时，则根据式(6)可得正方形极限状态函数：

G(Y,IM)=1-Y1或G(Y,IM)=1-Y2

(9)

④支座和桥墩两构件完全不相关时，根据式(6)可得凹形极限状态函数：

与浙东文人之“土性”形成鲜明对照的，是浙西人之温婉秀美(水性)。所谓“吴兴山水发秀，人文自江右而后，清流美士，余风遗韵相续”[26]之说者是。与此相应的是浙西文人“尚儒雅”的独特审美倾向与思维特质。晚近的鸳鸯蝴蝶派产生于吴文化区域(主要在江苏、上海，也包括浙西的杭嘉湖地区)绝非偶然。由是，浙西文人的文风中显出更多“飘逸”的特质。

G(Y,IM)=1-Y1且G(Y,IM)=1-Y2

(10)

四种多维极限状态函数所对应的极限状态面在三维空间的示意图如图1所示。图1中黑色区域表示桥梁系统处于安全状态，简称有效域；灰色区域表示桥梁系统处于破坏状态，简称失效域。

图1 极限状态函数示意图

(2)基于多维极限状态函数的系统易损性

根据多维极限状态函数，IDA曲线从安全域到失效域的变化过程中，可得到其与多维极限状态面的交点，即临界点(G=0)。根据式(11)计算桥梁系统在不同地震动作用下的破坏概率值[8]。

(11)

式中：Pf表示系统的失效概率；G(Y)表示多维极限状态函数；φ()表示标准正态分布函数；ηIM和βIM分别表示一组临界值IM的中位数及对数标准差。

2 工程算例与地震动的选取

2.1 工程概况与有限元模型

以某一连续刚构桥为工程背景，全桥总长440m，主跨108m，跨径布置(58+3×108+58)m。该桥的混凝土构件参数如表1所示。

表1 混凝土构件参数表

该桥的抗震设防烈度为8度，设计基本地震动加速度为0.15g，场地类别为Ⅱ类，场地特征周期为0.45s。

运用有限元软件Midas/Civil建立全桥模型，如图2所示。模型中主要构件的模拟见表2。

图2 全桥有限元模型

表2 有限元模拟

桥墩的塑性铰采用纤维铰的形式，支座与主梁、桥墩均为主从约束，支座和桥墩之间采用弹性连接。

2.2 地震动选取

将该桥址处的设计反应谱曲线作为目标反应谱，然后在PEER(美国太平洋地震研究中心)中选择与目标反应谱相近的10条天然地震动作为地震动输入。算例仅研究桥梁系统纵向易损性，无横桥向地震动的输入。

3 传统的地震易损性分析

3.1 破坏指标选取与量化

地震易损性分析中，一般将结构的破坏状态划分为基本完好、轻微破坏、中等破坏、严重破坏、完全破坏五个等级。选择位移延性比作为支座的破坏指标，选择曲率延性比作为桥墩的破坏指标。

支座以实际经验确定其五种破坏状态的界限值。利用X-Tract软件对桥墩的关键截面进行弯矩-曲率分析，计算纵筋首次屈服时的曲率，等效屈服时的曲率，混凝土压应变为0.004时的曲率以及极限曲率，并以这四个参数作为划分桥墩五种损伤状态的界限值[6]。限于篇幅，部分构件破坏指标的量化如表3所示。

表3 破坏指标的量化(部分构件)

3.2 地震响应分析

选择PGA作为IM参数，将PGA调幅为0.1g、0.2g、0.3g、0.4g、0.5g、0.6g、0.7g、0.8g、0.9g、1.0g，总共生成100条地震动进行非线性时程分析，得到支座、桥墩等构件的最大响应。在对数空间下进行IDA曲线的拟合，限于篇幅，仅列举部分构件的拟合参数如表4、表5所示。

表4 支座拟合参数表

表5 桥墩墩底拟合参数表

由表4、表5可知，在四种损伤状态下，IDA曲线的斜率a一致，截距b依次减小。

3.3 桥梁构件易损性曲线

基于破坏指标的确定及量化，IDA曲线的回归，将分析结果代入式(4)，得桥梁构件的破坏概率，并绘制构件地震易损性曲线，如图3所示。限于篇幅，仅列出了部分构件的地震易损性曲线。

图3 桥梁构件地震易损性曲线

假定桥梁构件在某一破坏状态下破坏概率值超过50%时会发生损伤。由图3可知，支座、桥墩发生轻微破坏时的PGA分别为0.24g、0.22g。

3.4 桥梁系统易损性曲线

基于桥梁构件易损性，根据式(5)得到桥梁系统的地震易损性曲线如图4所示。

图4 桥梁系统地震易损性曲线

由图4可知，在四种破坏状态下，桥梁系统的地震易损性均变为区间的形式，且破坏概率上下界限差最大值分别为27.7%、29.4%、29.3%、28.9%。

4 基于多维极限状态函数的地震易损性分析

4.1 地震响应分析

分别以支座的位移延性比Y1、桥墩的曲率延性比Y2为横坐标和纵坐标，以地震动强度IM为竖坐标进行空间IDA曲线的绘制。限于篇幅，仅列举桥梁在中等破坏状态下的空间IDA曲线如图5所示。

图5 空间IDA曲线(中等破坏)

由图5可知，随着IM的增加，桥梁构件支座和桥墩的响应值也逐渐增加。将上述空间IDA曲线投影到平面坐标系中，得到四种极限状态函数在四种不同损伤状态下的平面IDA曲线。限于篇幅，仅列举中等破坏状态下的二维投影曲线如图6所示。

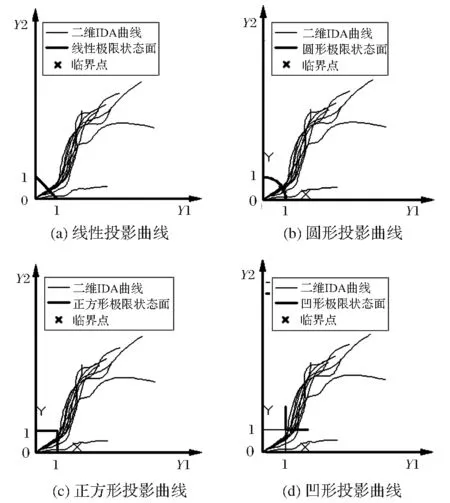
图6 投影曲线图(中等破坏)

由图6可知，在中等损伤状态下，不同的极限状态函数面与IDA曲线的交点不同，即临界点不同。

4.2 系统易损性

根据4.1节IDA曲线的绘制获得一系列的临界点，并求得四种多维极限状态函数在不同破坏状态下的地震动强度中值ηIM与对数标准差βIM，如表6所示。限于篇幅，仅列举中等破坏状态下的相关参数。

将表6中所得相关参数代入式(11)中，基于破坏概率值桥梁系统地震易损性曲线如图7所示。

表6 IM相关参数表(中等破坏)

由图7可知，在PGA一定的情况下，线性相关易损性>非线性相关易损性>完全相关易损性>完全不相关易损性。其中，基于线性相关函数的易损性与基于完全不相关函数的易损性相差较大。

图7 桥梁系统易损性

5 结论

以某一连续刚构桥为算例，比较了传统的易损性分析方法与基于多维极限状态函数的地震易损性分析方法，得到结论如下：

(1)传统的地震易损性分析方法得到的桥梁系统地震易损性曲线来源于桥梁构件的易损性曲线，并且表达为区间的形式，上下界差值最大为29.4%，无法准确描述桥梁结构的损伤状态。

(2)基于多维极限状态函数的桥梁地震易损性分析方法中可直接利用桥梁结构在地震动作用下的响应值得到桥梁系统地震易损性曲线，用于描述桥梁结构的损伤状态。

(3)考虑桥梁构件之间可能存在不同的相关性后，利用不同的多维极限状态函数所得到的桥梁系统地震易损性相差较大。其中，桥梁构件支座和桥墩之间线性相关时，地震易损性最大；非线性相关次之；完全相关次小；完全不相关最小。故在后续桥梁地震易损性研究中应着重考虑桥梁各构件之间的相关性对桥梁系统的影响。