等强度梁理论在SSMP连接器接触头结构优化中的应用
2022-06-28党作红
车 轰,陈 原,党作红,雷 杰
(中航富士达科技股份有限公司,陕西西安,710077)
1 引言
SSMP型连接器是一种超小型推入式射频同轴连接器,广泛应用于通信、航天、军工等领域。SSMP连接器中接触头零件是传递信号的核心部件[1],其机械耐久型是SSMP连接器最重要的机械性能之一。
现有SSMP连接器接触头工作时,其簧片应力分布不均匀,在劈槽根部存在应力集中现象,并且簧片应力较大,极限工况下,簧片甚至发现断裂现象,如图1.1所示。因此,对接触头结构进行优化设计,以降低接触头簧片变形时的最大应力,进一步降低接触头簧片断裂风险,就显得尤为重要,同时,对提高接触头耐久性也具有重要意义。

图1.1 SSMP接触头簧片断裂示意图
本文基于等强度梁理论,提出接触头结构优化方案,并使用ANSYS Workbench有限元软件对接触头各参数尺寸与接触头簧片最大应力以及最大正压力进行敏感度分析,以确定设计变量。同时对优化后的接触头结构进行实际工况力学仿真,并通过实验验证优化后接触头的机械性能,以说明优化方案的可行性及优点。
2 等强度梁理论
梁的弯曲正应力σ计算公式如式(1)所示[2]。其中,M为弯矩,W为抗弯截面系数,对于恒截面梁,抗弯截面系数W为常量,其应力最大值出现在弯矩最大的截面上,而在其余截面上应力较小,对于悬臂梁,在梁的自由端应力最小,在梁的固定端应力最大,整个梁上应力分布不均匀,材料利用不合理。
(2.1)
若在弯矩较大的部位采用较大截面,在弯矩较小的部位采用较小截面,使得梁截面沿轴线发生变化,将恒截面梁变为变截面梁,如图2所示。
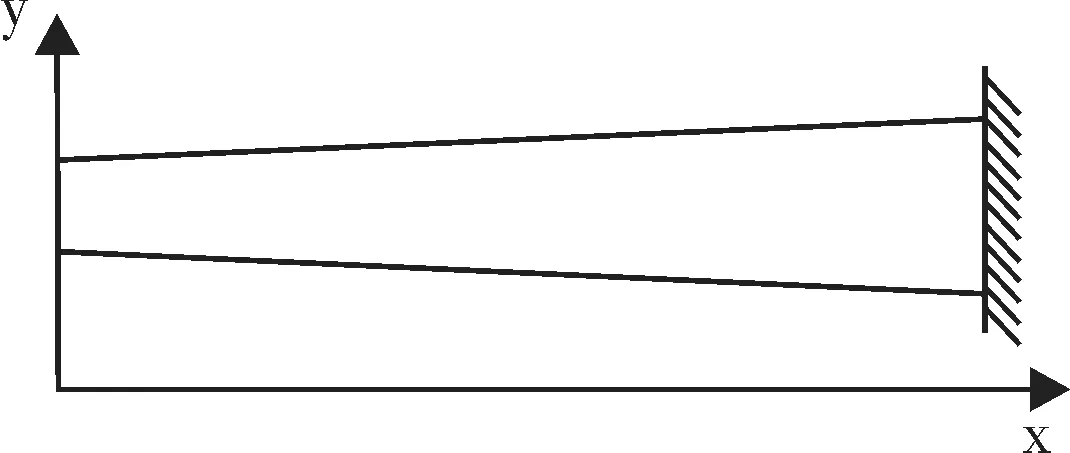
图2.1 变截面梁示意图
则上述变截面梁弯曲正应力计算公式为:
(2.2)

图2.2 梁截面示意图
若梁截面为如图3所示的矩形,对于图1所示悬臂梁,其截面宽度b为常量,高度h为沿梁轴线距离x的函数,假设高度h为沿梁轴线距离x的一次函数,即h(x)=kx+c,则抗弯截面系数W(x)将变为:
(2.3)
将2.3式代入2.2式,得出变截面梁弯曲正应力计算公式为:
(4)
若弯矩保持不变,增大截面高度h(x)的函数曲线斜率k值,根据式(4),变截面梁自由端应力将变大,固定端应力将变小,若使梁上各截面的应力都相等,且都等于许用应力,则称这种梁为等强度梁。同样,通过调整截面高度h(x)的曲线斜率K,可在恒截面梁的基础上,进一步降低梁的最大应力,达到优化结构的目的。
3 SSMP接触头结构优化
3.1 设计变量的确定
SSMP连接器接触头工作时,其簧片力学模型可简化为悬臂梁[3]。由于优化目标为:在保证接触头分离力和啮合力满足标准的情况下,接触头簧片最大应力最小,因此优化参数应该为与接触头分离力、啮合力以及接触头簧片最大应力相关联的尺寸,根据悬臂梁理论,与接触头分离力、啮合力以及接触头簧片最大应力相关的接触头尺寸为接触头内径d1、接触头外径d2、接触头簧片自由端径向变形量A、劈槽长度L、以及接触头尾部直径d3。
因此,将以上参数作为初选的设计变量,对于变截面接触头,接触头外径尺寸分为头部外径尺寸d2和根部外径尺寸d4,各尺寸结构示意图如图3.1所示。
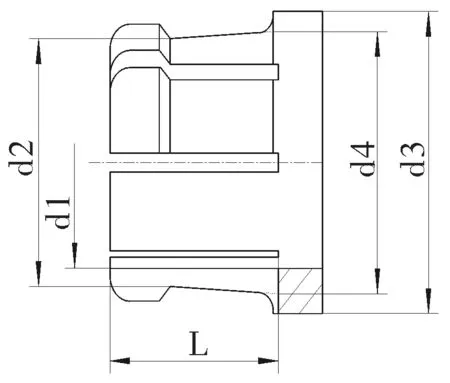
图3.1 变截面接触头结构示意图
由于上述优化参数较多,为减少接触头结构优化过程的工作量,需对上述优化参数进一步删减,由于接触头内径尺寸d1不仅影响接触头簧片最大正压力和最大应力,还影响SSMP连接器电性能,因此首先剔除接触头内径尺寸。剩余尺寸需要与接触头簧片最大正压力和最大应力进行敏感度分析,以找出对最大应力影响较大的尺寸。
在对接触头尺寸进行敏感度分析时,以接触头为研究对象,在ANSYS Workbench有限元软件中建立接触头有限元模型,通过改变单个尺寸,以建立各个尺寸与最大正压力和最大应力的关系曲线,从而分析单个尺寸与最大正压力和最大应力的变化关系。每种尺寸与最大正压力和最大应力关系曲线如图3.2、图3.3、图3.4、图3.5以及图3.6所示。

图3.2 头部直径d2-最大应力和最大正压力关系曲线
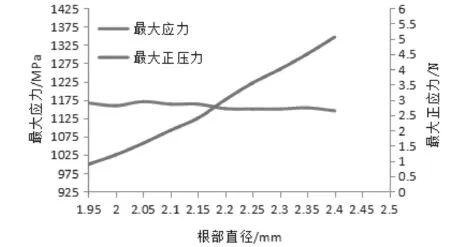
图3.3 根部直径d4-最大应力和最大正压力关系曲线

图3.4 尾部直径d3-最大应力和最大正压力关系曲线

图3.5 劈槽长度L-最大应力和最大正压力关系曲线
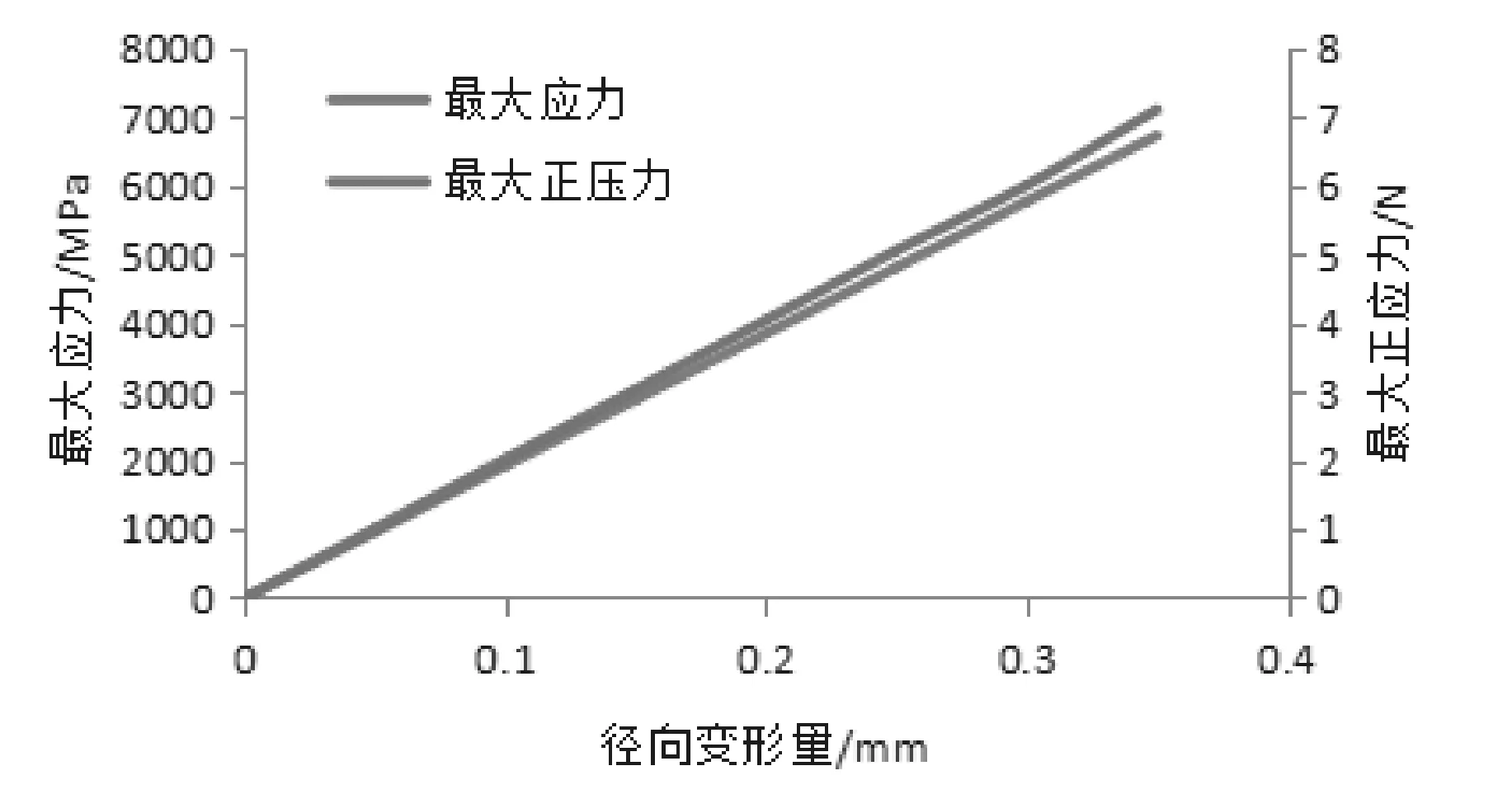
图3.6 径向变形量A-最大应力和最大正压力关系曲线
由上图可以看出,头部直径尺寸d2、劈槽长度L、径向变形量A和尾部直径d3与最大应力关系曲线的斜率较大,可见上述参数的改变对最大正压力有较大影响。由于本次结构优化是以接触头簧片最大应力最小化为优化目标,因此,根据上述分析选定头部直径尺寸d2、劈槽长度L、径向变形量A以及尾部直径d3为最终的设计变量。
3.2 边界条件的选取
根据上一节确定的设计变量,以接触头簧片最大应力最小化为优化目标,对接触头结构进行优化。
由于未推导出变截面接触头簧片最大应力和最大正压力理论计算公式,变截面接触头结构优化的目标函数为隐函数形式,因此本次优化借助有限元软件进行参数的寻优。
最终优化结果如表3.3和表3.4所示。

表3.3 SSMP接触头优化结果

表3.4 优化前后最大等效应力对比结果
从表3.4可以看出,对插光孔规时,优化后接触头簧片最大等效应力为843.9MPa,已经小于铍青铜的弹性极限,并且,从图3.7和图3.8可以看出优化后变截面接触头簧片最大应力向簧片自由端迁移,应力分布更均匀,材料利用更合理。
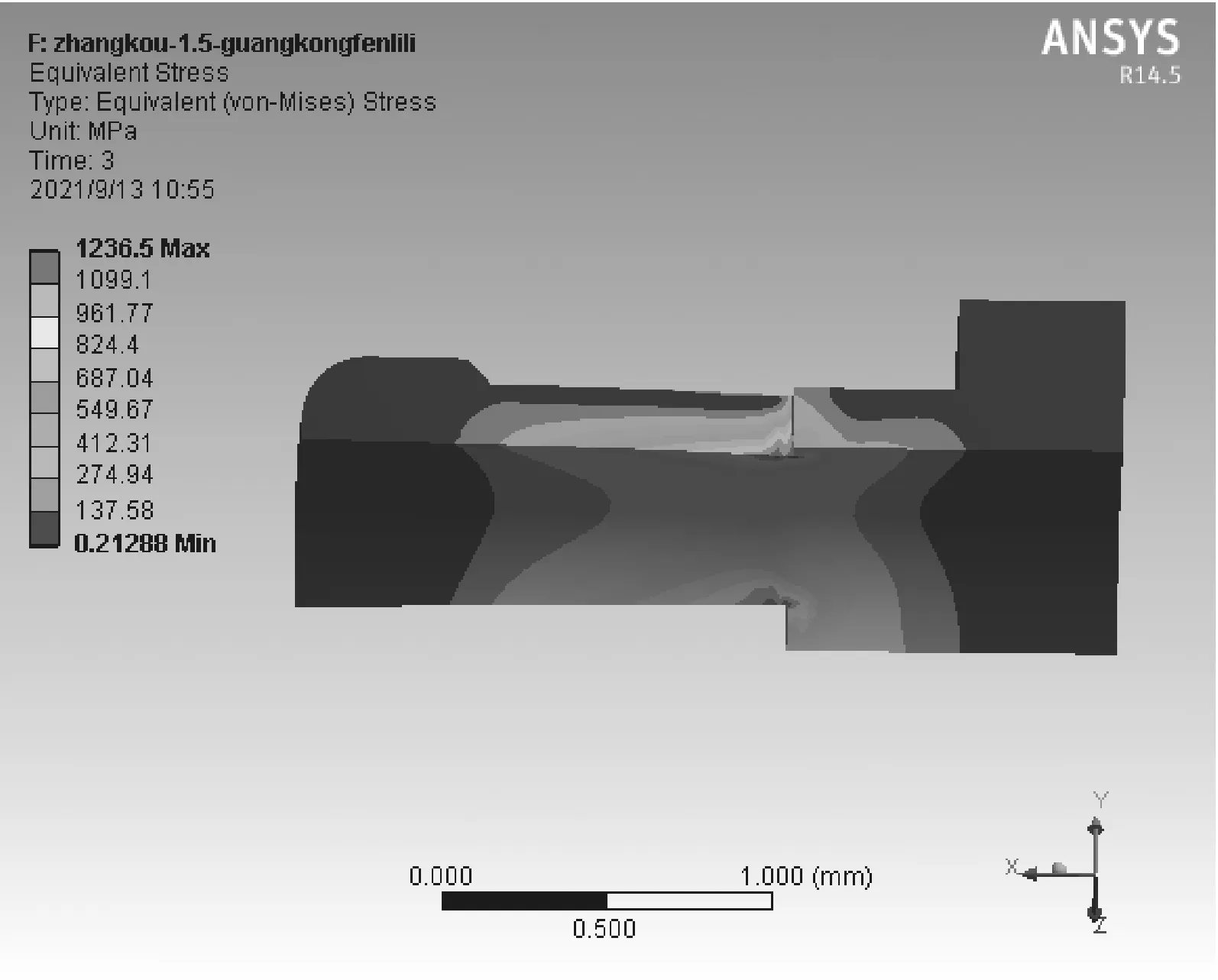
(a) 优化前对插光孔端簧片应力云图

(a) 优化前对插擒纵端簧片应力云图
4 实验验证
对优化设计后的接触头进行试制,并验证接触头分离力、啮合力以及插拔寿命,验证结果如下:
(1)有限元仿真模型验证
根据表4.1数据,求得光孔规分离力实测值与仿真值平均误差为12.7%,小于15%,在可接受范围内,这种误差主要来源于如下几方面:

表4.1 光孔规分离力仿真值与实测值对比
a.仿真时将接触头与测试规内孔之间的摩擦系数设定为0.2,与实际摩擦系数存在差异。
b.仿真时设定的材料弹性模量是按照HV350硬度值对应的材料弹性模量设定的,而实际材料硬度存在误差,从而造成仿真值与实际值的不相符。
c.实际接触头加工时存在的加工误差。
(2)分离力和啮合力验证结果
分离力和啮合力部分试验结果如表4.2所示。
从表4.2可以看出,优化后接触头的分离力和啮入力满足要求。

表4.2 分离力和啮合力实验结果
(2)接触头插拔寿命验证
光孔端插拔寿命试验数据如表4.3所示
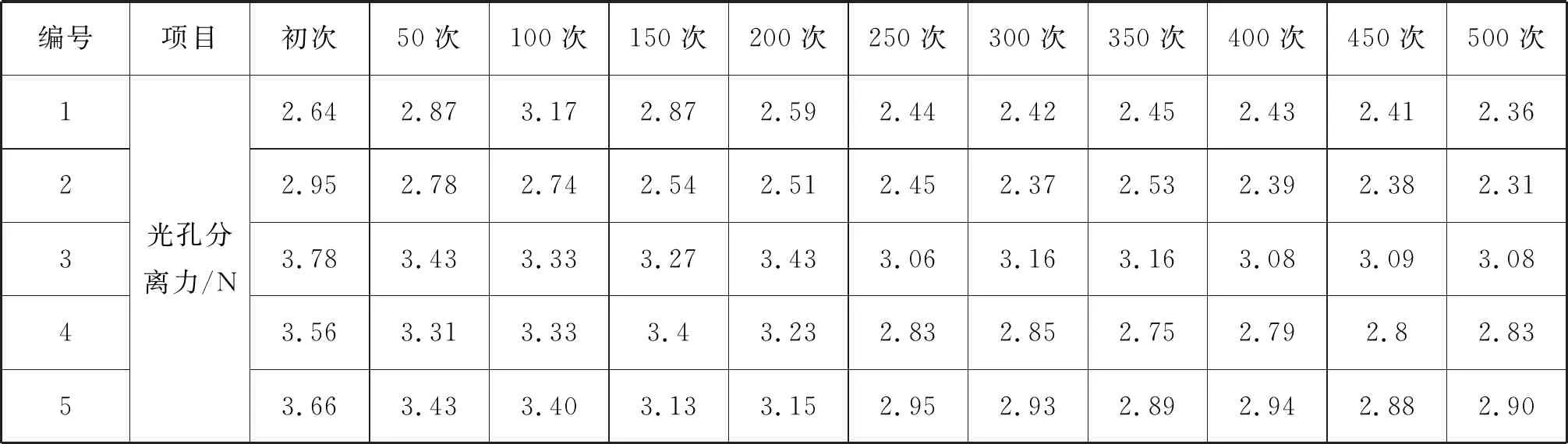
表4.3 光孔端插拔寿命验证数据
擒纵端插拔寿命试验数据如表4.4所示

表4.4 擒纵端插拔寿命验证数据
根据表4.3和表4.4的试验结果,光孔端插拔寿命和擒纵端插拔寿命均符合要求。
5 结束语
(1)本文基于等强度梁理论,针对现有SSMP连接器接触头存在的问题,提出SSMP接触头优化方案。结果表明,优化后接触头对插光孔分离力规时,接触头簧片最大等效应力已经小于材料的弹性极限,并且接触头簧片最大应力向簧片自由端迁移,应力分布更加均匀,为此类接触头结构设计提供了依据。
(2)本文建立了SSMP接触头有限元模型,并使用ANSYS Workbench有限元软件得出接触头各尺寸与最大应力以及最大正压力关系曲线图,以对接触头各尺寸与最大应力以及最大正压力进行敏感度分析。
(3)本文对优化后接触头进行相应实验验证,实验结果表明优化后接触头满足耐久性及相应力值要求。
