毛刷电接触对的接触电阻研究

梁云忠，乔玉鹏，伍 权，徐卫平



毛刷电接触对的接触电阻研究

梁云忠，乔玉鹏，伍 权，徐卫平

（贵州师范大学 机械与电气工程学院，贵州 贵阳 550001）

基于R.holm电接触理论建立了毛刷电接触对的接触电阻模型。采用有限元仿真确定了毛刷电接触对在插拔过程中只有弹性变形，并得到了接触电阻模型中的值为1/2，进行了毛刷电接触对不同插拔深度上的接触电阻试验，通过试验数据拟合确定了毛刷电接触接触电阻模型中的值为248。进行了毛刷、麻花针、线簧孔接触对在不同插拔深度的接触电阻对比试验，得到了毛刷电接触插拔深度的最优范围为2~2.2 mm，进行了毛刷电接触在2~2.2 mm插拔深度时接触电阻寿命试验，基于接触电阻寿命曲线提出了预插拔工艺以提高接触电阻及插拔力的稳定性。毛刷电接触接触电阻研究为毛刷电接触的扩展设计、制造提供了参考。

毛刷电接触；接触电阻模型；插拔深度；预插合；插拔寿命；电连接器

20世纪80年代以来，在参考美国军用电连接器标准的基础上，我国逐步研制出绞线麻花针电接触对、开槽弹性插孔电接触对以及线簧孔电接触对等一系列高可靠的电接触形式，为我国的军用电连接器发展奠定了坚实的基础。近年来，随着集成电路的飞速发展，整机系统要求电连接器芯数越来越多，插拔寿命越来越长，开槽弹性插孔等电接触对由于插拔力过大、插拔寿命短等缺点，导致大芯数电连接器在多次插拔分离时连接器接触失效、印制板及系统部件破坏等问题。因此寻求高可靠、长寿命、低插拔力的电接触形式成为国内外研究学者和生产商的关注焦点[1-6]。毛刷电接触对因其轻插拔力，耐磨损、优异的电接触性能开始用于航空、航天等高可靠连接器上。在国外，美国领军电子元件生产商Amphenol公司在2002年首先将装配有毛刷电接触对的系列连接器用于美国第五代战机F35中并几乎垄断了该型号战机的所有印制电路连接器。在国内，主流军用电连接器相继投入到毛刷电接触对的研发中，并研发了装配有毛刷电接触件的各类新品[7]。

根据霍尔姆电接触理论，电接触对的接触电阻与插拔力有着紧密关系，插拔力大，接触电阻小，且不同的电接触结构，其函数的相关系数不同。在电连接器可靠性设计中，保证不太低的插拔力是为了保证接触对有较小的接触电阻，从而有效控制电连接器的温升[8-11]。

在毛刷电接触对理论研究方面，《毛刷电接触对的插拔力研究》[12]一文研究了毛刷电接触对的插拔力模型，对毛刷电接触插拔力进行仿真，并与其他形式接触对进行了插拔力对比试验。但是毛刷电接触对的接触电阻模型及相关接触电阻可靠性试验目前尚未见相关研究。

本文根据毛刷电接触的插拔力模型，分析毛刷电接触对接触电阻影响因素，通过有限元仿真分析、试验等方法并建立毛刷电接触对的接触电阻计算模型；对毛刷电接触对进行接触电阻的插拔寿命试验，为毛刷电接触的规格扩展及相关毛刷电接触类电连接器的插拔深度设计提供参考。

1 毛刷电接触对接触电阻模型建立

1.1 毛刷电接触对原理

如图1所示，毛刷电接触对由插针及插孔组成，插针、插孔的电接触部分由一束单针压接在一起，整个电接触被限制在插孔护管内。在插针与插孔插合的过程中，两端单针被相互撑开，插针和插孔的单针之间随机相互插合在一起，从而形成电气连接。

图1 毛刷电接触示意图

1.2 毛刷电接触对接触电阻模型的建立

电接触学科奠基人霍尔姆（R.holm）认为接触电阻由接触元件两边的收缩电阻s与接触面之间的膜电阻b组成，此外霍尔姆还通过试验确定了收缩电阻、膜电阻与接触对插拔力之间为指数函数关系。由于三者在电路上处于串联关系，考虑接触材料相同，接触面两边的电流场对称，因此接触电阻可以表示为：

式中：值为接触材料的函数，同时与表面的膜情况有关，其值由试验决定；与接触面变形情况有关，弹性变形为1/2，塑性变形为1/3[13-17]。

由公式（1）可知，毛刷电接触对的接触电阻与插拔力有密切关系。在参考文献[12]中，根据毛刷电接触单针在插拔过程中属于悬臂梁结构，推导出毛刷电接触对插拔力模型公式为：

综合公式（1）、（2）可得毛刷电接触对的接触电阻模型公式为：

式中：为接触件插拔深度；为单针接触处变形量设计值；为单针长度；为单针数目；为单针截面的惯矩；为单针材料的杨氏模量。

由公式（2）可知，毛刷电接触对接触电阻与单针接触处变形量设计值平方成正比、且与值，值，单针材料的杨氏模量以及单针截面的惯矩相关。

为确定毛刷电接触对接触电阻模型公式（3）式中的、值，本文采用有限元仿真及实验数据拟合等方式来确定。选用毛刷接触对中典型规格尺寸进行试验或有限元仿真，试验样件的规格参数如下：接触件材料铍青铜C17500（=120 GPa），表面镀金1.27 mm，护管直径为=1.36 mm，单针直径=0.2 mm、单针长度=4 mm，单针变形量设计值=0.065 mm，单针数目=7。

试验条件如下：接触电阻的测试采用同批镀金的未插合过的毛刷电接触对，且测试时温度保持为22℃，相对湿度保持73%，试验电流1 A。

毛刷电接触对试验样品如图2所示。

图2 毛刷电接触试验样品

1.3 基于有限元仿真的值确定

在插拔过程中难以观察到接触件的变形情况，因此采用ADINA软件分析毛刷对接触对插拔过程中单针的变形情况，在毛刷电接触模型建立时，将毛刷电接触插孔及单针固定，对接时仅插针端单针簇可产生变形。设置毛刷电接触对插针端一个径向位移，使其完成插入过程。为了能正确模拟出插入对接过程，对接的单针之间以及单针和护管之间需设置接触对。材料可能产生弹性变形及塑性变形，因此设置为双线性弹塑性材料，完成如图3所示的前处理设置。

图3 有限元前处理设置

分别取毛刷电接触件对1 mm插拔深度和3 mm插拔深度，查看这两个时间点的整体应力分布情况如图4、图5所示，可以看出插拔过程中最大的应力分布在单针上，且最大应力为110 MPa，远小于铜等材料的屈服强度，因此插拔过程中单针仅发生弹性变形。

图4 插入深度1 mm时刻应力分布图

图5 插入深度3 mm时刻应力分布图

由仿真过程可知，单针在插拔范围内发生弹性变形，根据R.holm电接触理论，取值为1/2。

1.4 基于不同插拔深度接触电阻试验的值确定

选择毛刷接触对中典型规格尺寸进行试验，取10对毛刷接触对中进行接触电阻测试试验，分别测试每个接触对在0.5，1.0，1.5，2.5，2.5，3.0，3.5 mm插拔深度上的接触电阻值，并计算平均值作为纵坐标。试验结果如图6所示。

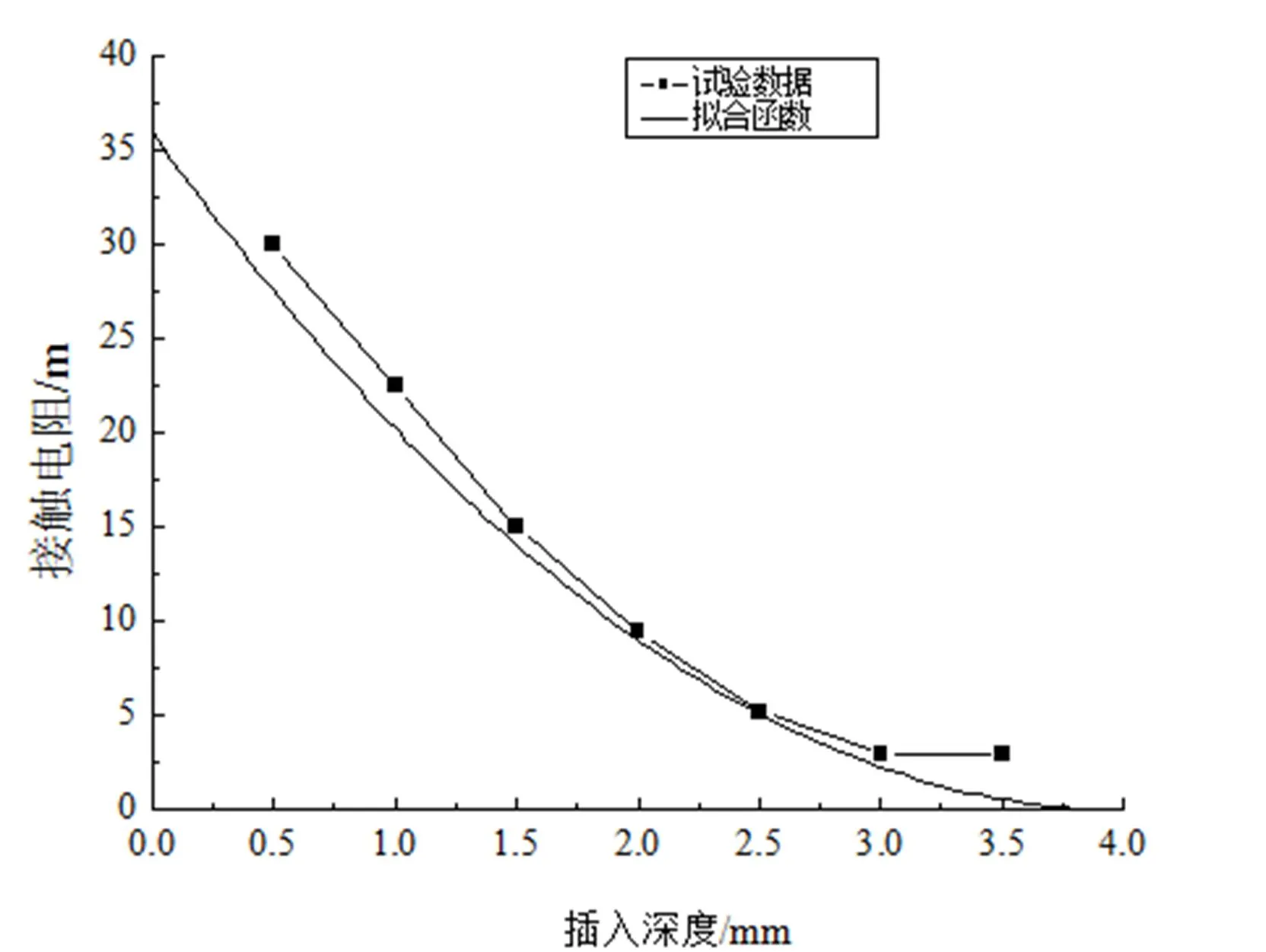
图6 不同插拔深度的接触电阻

根据试验数据进行线性拟合，可拟合出接触电阻与插入深度的拟合公式为：

= 2.246 9(4–)2（4）

将公式（3）的各参数代入并与公式（4）进行比较，可知取值为248。综上所述，可知常用规格毛刷电接触对接触电阻模型公式为：

2 毛刷电接触对与线簧孔、麻花针电接触对接触电阻试验对比

为比较毛刷电接触对与其他常用军用电接触对的接触电阻差异，选择与典型规格毛刷电接触对相近尺寸的麻花针、线簧孔接触对进行不同插拔深度的插拔力对比试验。图7为三种接触对在不同插拔深度的接触电阻试验数据对比。

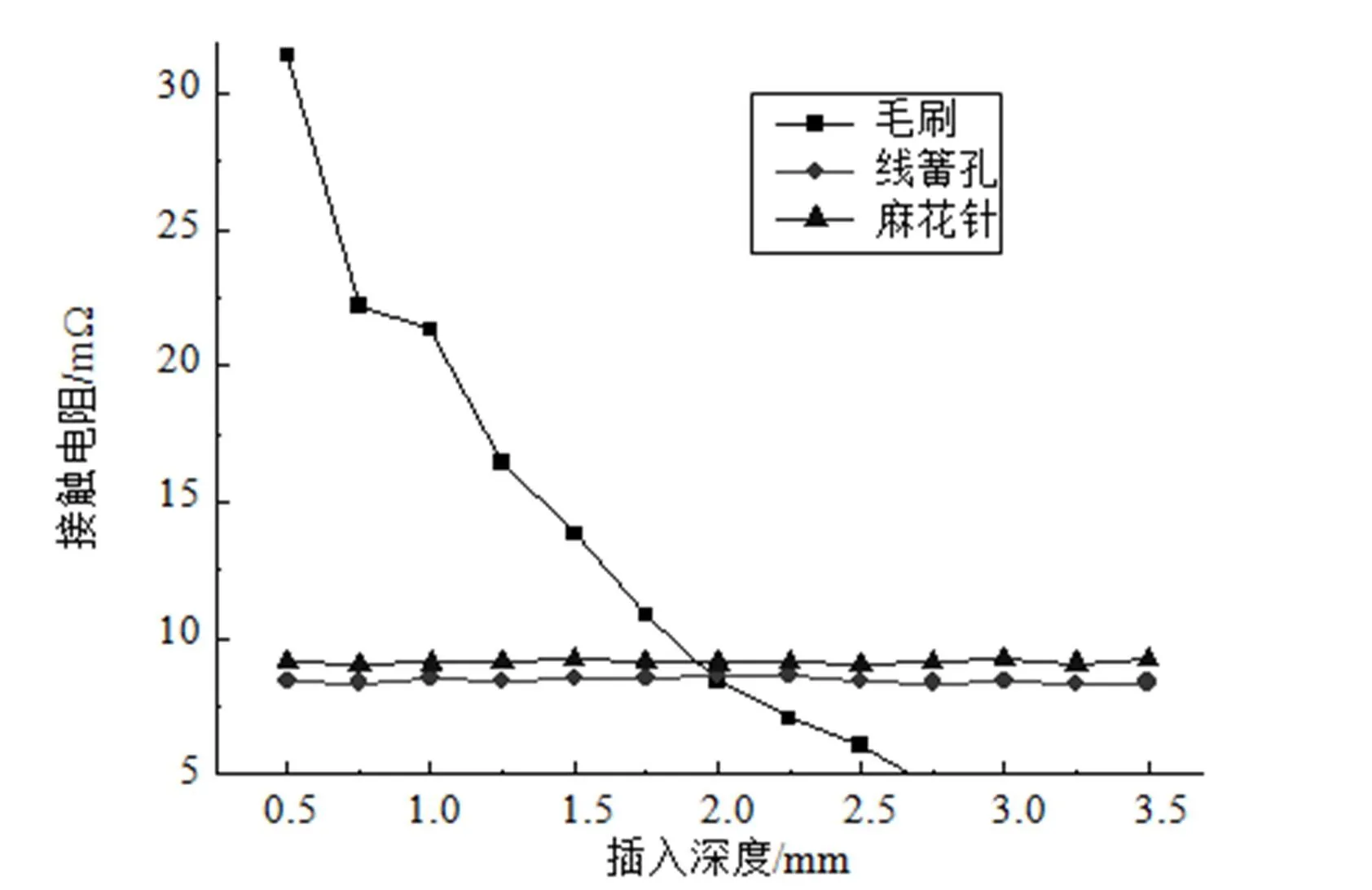
图7 毛刷、线簧孔、麻花针电接触对在不同插拔深度的接触电阻

由图7对比可知：

（1）毛刷电接触对的接触电阻随插拔深度变化显著变化，而麻花针、线簧孔接触电阻不随插拔深度的变化而变化。原因为毛刷电接触的插拔力与插拔深度相关，插入深度越大，插拔力越大，插拔力增大导致接触电阻减小；麻花针、线簧孔接触件插拔力与插拔深度无关，故接触电阻没有变化。

（2）毛刷电接触的接触电阻随插拔深度增大而减小，但是当插拔深度越接近单针长度，接触电阻几乎不再变化。其原因为当插拔深度越大，插孔端单针已经紧贴护管壁，不再有弹性变形量的增大，故插拔力不再增大，接触电阻也就几乎不再变化。

（3）接触电阻小的接触件会使连接器温升降低，因此与麻花针、线簧孔接触件相比，毛刷电接触的接触电阻在插拔深度大于2.0 mm时，其接触电阻较麻花针及线簧孔接触件小，结合参考文献[12]，毛刷电接触相对线簧孔及麻花针接触件具备较小插拔力的合理范围为1.8~2.2 mm，因此在多芯数（100芯以上）印版版连接器设计中，毛刷电接触对的插拔深度设置为2.0~2.2 mm时，毛刷电接触接触电阻较小，且插拔力也较毛刷电接触小，从而在多芯数印制板连接器中具有插拔力和接触电阻的优势。

3 接触电阻的插拔寿命试验

为验证毛刷电接触在合理插拔深度2.0~2.2 mm上的插拔寿命可靠性，将装有20芯典型规格毛刷接触对的电连接器进行插拔试验，连接器试验插拔深度为2.0~2.2 mm，插拔次数设计为=104次。在试验时，间隔检测插拔后平均接触电阻。

依次选取不同的插拔次数为横坐标，测得的平均接触电阻为纵坐标，建立起平均接触电阻的寿命试验数据，如图8。

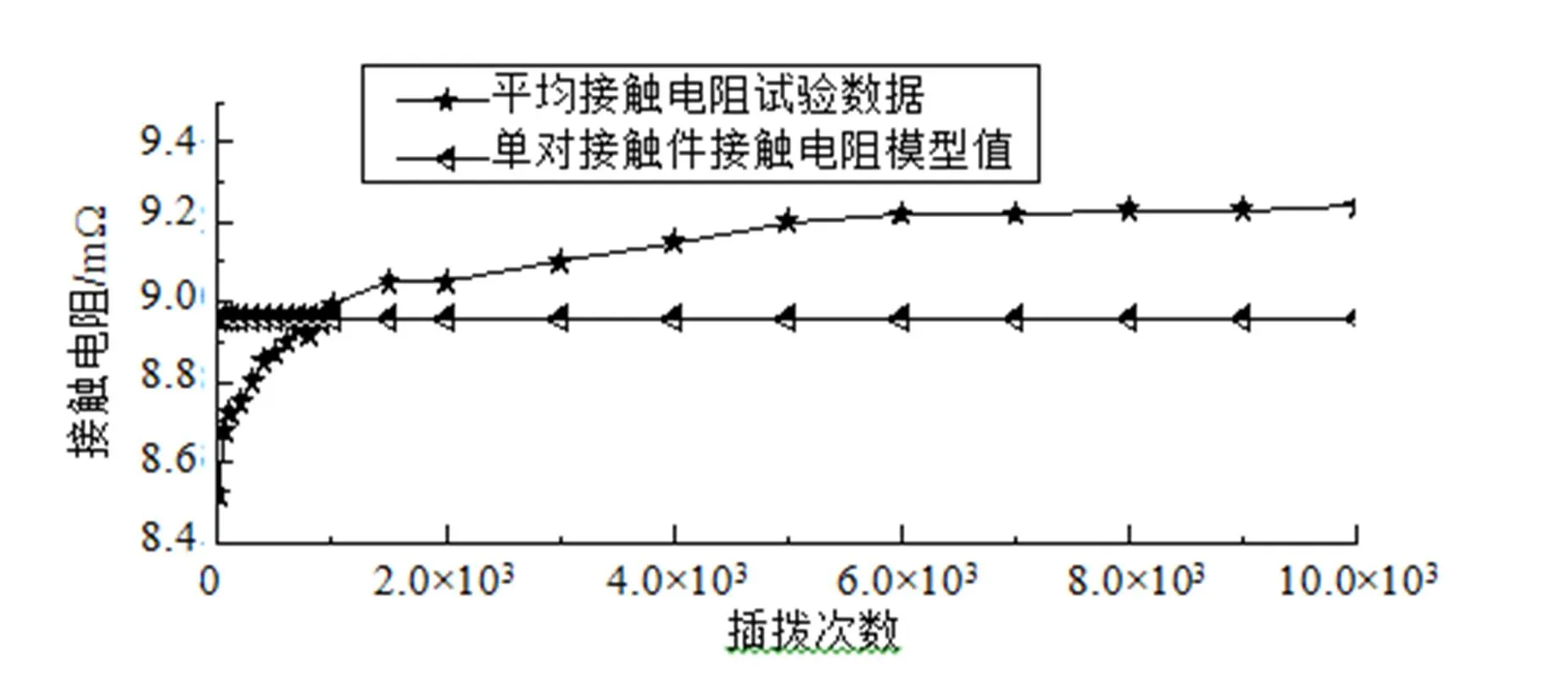
图8 接触电阻的万次寿命试验（插拔深度2.0~2.2 mm）

由图8可知：

（1）在2 000次插拔次数范围内，平均接触电阻随插拔次数增加而显著增大，在2 000次插拔次数后，平均接触电阻逐步趋于平稳。导致此原因为2 000次插拔导致了毛刷接触对的单针有一定量的塑形变形，塑性变形导致单针变形量减小，因此导致了插入力的减小及接触电阻的增大；随着该塑性变形趋于稳定，接触电阻也趋于稳定。

（2）在2 000~10 000次插拔范围内，接触电阻随插拔次数趋于稳定，因此说明在2 000次范围内的插拔导致的单针塑性变形并没有导致电接触对失效，而是电接触对在经过2 000次磨合插合以后，进入了可靠工作阶段。

（3）2 000次插拔次数范围内，接触电阻随插拔次数而增大，在精密系统使用时会导致一定误差，此外由于平均插入力随插拔次数增加而显著减小，在人工插拔过程中插拔手感会显著变化，因此在产品生产完毕后可首先进行2 000次左右的预插拔后使用，这样连接器的插入力及接触电阻更加稳定。

4 结论

（1）根据霍尔姆（R.holm）电接触理论和毛刷电接触的插拔力模型，建立了毛刷电接触对的接触电阻模型。

（2）根据毛刷电接触插合过程中的有限元仿真，毛刷电接触单针仅发生弹性变形，确定了电阻模型中的值为1/2，通过不同插拔深度下的接触电阻试验值确定了接触电阻模型中的值为248。

（3）进行了相近规格的毛刷电接触、线簧孔接触件、麻花针接触件在不同插拔深度时的接触电阻试验，并得到了毛刷电接触对相对线簧孔及麻花针接触件具备插拔力及接触电阻优势的深度插拔范围为2.0~2.2 mm。

（4）进行了毛刷电接触在2.0~2.2 mm的10 000次接触电阻插拔寿命试验，根据寿命曲线提出了预插拔工序，使毛刷电接触的连接器插拔力和接触电阻性能更加稳定。

[1] 杨奋为. 军用电连接器的应用与发展 [J]. 机电元件, 2012(4): 52-61.

[2] SAWCHYN I, SPROLES E J. Optimizing force and geometry parameters in design of reduced insertion force connectors [J]. IEEE Trans Compon Hybrids Manuf Technol, 1992, 15(6): 1027-1031.

[3] 潘骏, 靳方建, 陈文华. 电连接器接触件结构分析与插拔试验 [J]. 中国机械工程, 2013, 24(4): 1636-1641.

[4] LI Z G, JIANG D, LI W H, et al. Reliability analysis and failure prediction study of dynamic contact resistance on contact [C] //Proceedings of 48th IEEE Holm Conference Electrical Contacts. New York: IEEE, 2002: 61-65.

[5] CHEN W H, MA Z K, GAO L, et al. Quasi-statie analysis of thrust-loaded angular contact ball bearings partl: theoretical formulation [J]. Chin J Mech Engin, 2012, 25(l): 71-80.

[6] 潘骏. 航天电连接器振动可靠性建模与评估 [D]. 杭州: 浙江大学, 2002: 12-14.

[7] 刘刚. 刷状接触件: 中国: 2009201252733 [P]. 2009-03-05.

[8] HOL M R. Electrical Contacts [M]. New York: Springer, 1979.

[9] 马东娟. 多变量灰色模型MGM(1,)在电磁继电器特性参数分析中的应用研究 [J]. 电子元件与材料, 2014, 33(12): 78-81.

[10] 王玲, 万超, 朱姗, 等. 导电胶导电/导热性能影响因素研究 [J]. 电子元件与材料, 2014, 33(2): 16-18.

[11] 李奎, 张冠生, 陆俭国. 含膜触头静态接触下接触电阻有限元模型及其分析 [J]. 电工技术学报, 1998, 13(1): 18-30.

[12] 梁云忠, 乔玉鹏, 金波, 等. 毛刷电接触对的插拔力研究 [J]. 工程设计学报, 2015, 22(3): 290-294.

[13] TAMAI T. Effect of humidity on growth of oxide film on surface of copper contacts [J]. IEICE Trans Electron, 2007, E90-C(7): 1391-1397.

[14] READ M B, LANG J H, SLOCUM A H. Contact resistance in flat thin films[C]. The 55th IEEE Holm Conference on Electrical Contacts. NY, USA: IEEE, 2009: 300-306.

[15] BOYER L. Contact resistance calculations: generalizations of greenwood’s formula including interface films [J]. IEEE Trans Compon Packag Technol, 2001, 24(1): 50-58.

[16] ALEŠ D, PAVEL M. Analysis and prediction of electrical contact resistance for anisotropic conduc-tive adhesives [C]// Electronics Technology of the 31st International Spring Seminar. NY, USA: IEEE, 2008: 358-362.

[17] MELIDA C, HU S J. A multiple particle model for the prediction of electrical contact resistance in anisotropic conductive adhesive assemblies [J]. IEEE Trans Compon Packg Technol, 2007, 30(4): 745-753.

Study on contact resistance of brush electrical contact

LIANG Yunzhong, QIAO Yupeng, WU quan, XU Weiping

(Department of Mechanical and Electrical Engineering, Guizhou Normal University, Guiyang 550001, China)

The contact resistance model of the brush electric contact was established based on R.holm electric contact theory. In the process of insertion and extraction of the brush electrical contact, only elastic deformation was got by finite element simulation andvalue of the contact resistance model was obtained (1/2), the contact resistance tests on different insertion depth of the brush electrical contact were done andvalue of the brush electric contact resistance model was obtained（248）by means of experimental data fitting. The contact resistance test in different insertion depth of the brush, the spring wire socket and twist-pin electrical contact were carried out. The results show that the advantage range of insertion depth of the brush electric contact is 2.0－2.2 mm. Contact resistance life test of the brush electrical contact in 2.0－2.2 mm insertion depth were done for ten thousands times, pre insertion technology was proposed according to the change of contact resistance in the test. Study on contact resistance of the brush electrical contact can provide a reference for the extensive design and manufacture of brush electrical contact.

brush electric contact; contact resistance model; insertion depth; Pre insertion technology; insertion life; connector

10.14106/j.cnki.1001-2028.2016.10.010

TN405

A

1001-2028（2016）10-0045-04

2016-07-09

梁云忠

贵州省自然科学基金资助项目（No. 黔科合LH字[2014]7043号）

梁云忠（1983－），男，贵州仁怀人，讲师，硕士，主要从事电接触理论和电连接器设计研究，E-mail:290263424@qq.com。

网络出版时间：2016-09-29 10:08:47

网络出版地址：http://www.cnki.net/kcms/detail/51.1241.TN.20160929.1008.010.html

（编辑：曾革）