模拟自由边界对卫星动力学特性的影响

刘明辉，刘闯，向树红，韩晓健，周春燕2，邹雍

（1.北京卫星环境工程研究所，北京 100094；2.北京理工大学宇航学院，北京 100081；3.重庆长安汽车股份有限公司，重庆 400023）

0 引言

随着高精度遥感观测卫星的研制和应用，卫星在轨微振动问题日益受到关注，国内外航天器研究机构广泛开展了高精度遥感观测卫星的地面微振动试验，以验证控制力矩陀螺、制冷机等星上含可转动部件设备引起的卫星结构微振动对精密光学相机和激光通信载荷指向精度的影响。

卫星在轨自由边界模拟是高精度遥感观测卫星地面微振动试验的关键技术之一。工程中广泛采用弹性支撑或悬吊的方法进行卫星在轨自由边界模拟，包括空气弹簧支撑方法、金属弹簧悬吊或支撑方法等。文献[7-8]分析了卫星微振动试验中模拟自由边界频率对卫星动力学特性的影响；文献[9]提出一种考虑金属弹簧静载变形的模拟自由边界频率设计与分析方法；国内外试验标准规定了模拟自由边界的频率范围，即支撑或悬吊频率应低于试验件自由状态下第一阶非刚体模态频率的25%：模拟自由边界频率设计与分析方法日趋成熟和规范。

微振动试验要求模拟自由边界对航天器在轨结构动力学特性的影响尽可能小，以往的研究重点主要针对模拟自由边界的频率；而实际模拟自由边界装置在工程实现时不可避免会使用法兰等局部连接结构与卫星进行连接，这种局部连接结构以附加质量的形式作用于航天器，对航天器动力学特性也会产生一定影响，因此模拟自由边界的附加质量应远小于航天器自身质量。可见，除了满足自由边界频率要求外，对模拟自由边界引入的附加质量的影响进行量化研究也是十分必要的。

本文针对卫星微振动试验自由边界模拟的具体工程问题，结合理论建模、仿真分析与实验验证，研究模拟自由边界附加质量对卫星结构动力学特性的影响规律，旨在给出卫星微振动试验中模拟自由边界附加质量量化控制的参考。

1 理论模型与仿真

1.1 模拟自由边界简化模型

卫星地面微振动试验模拟自由边界状态下的简化动力学模型如图1 所示，图中：和分别代表离散简化后卫星的两部分质量，取为卫星固定界面第一阶模态的有效质量，取为第一阶模态的剩余质量，+=为卫星总质量；为模拟自由边界附加质量；和分别为和的位移；表示卫星刚度，表示模拟自由边界刚度。

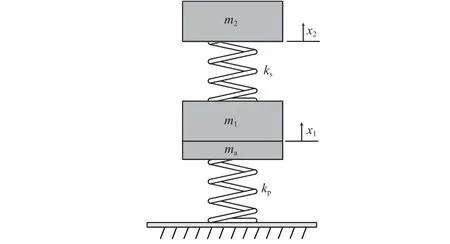
图1 卫星地面模拟自由边界简化分析模型Fig.1 Simplified analysis model of spacecraft under simulated free boundary condition

根据图1，卫星在地面模拟自由边界条件下的运动方程为

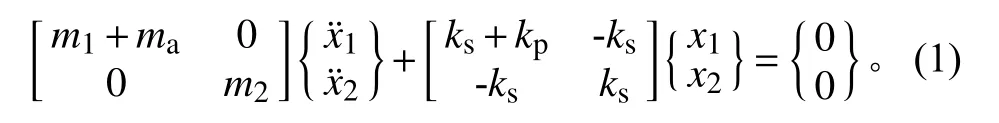
通过求解方程(1)的特征值，得到卫星在地面模拟自由边界下的模态频率为

式中：为模拟自由边界的频率；为模拟自由边界下卫星的模态频率；=(+)/，表示增加模拟自由边界附加质量后卫星总质量与原质量的比值；=(+)/，表示增加模拟自由边界附加质量后第一阶模态的剩余质量的变化。

根据式(2)，当模拟自由边界刚度相比卫星刚度较小时，忽略方程中的小量，可得到

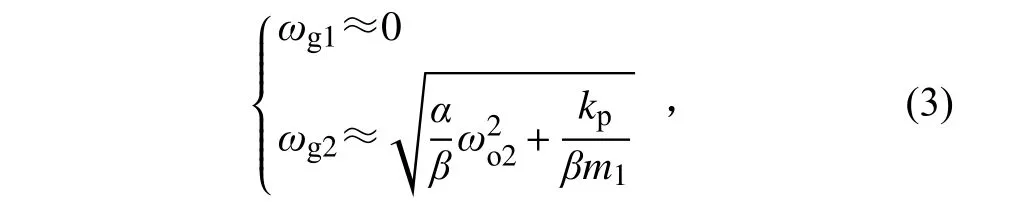
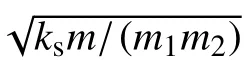
1.2 简化模型数值分析

通过数值分析对模拟自由边界下卫星的模态频率和频率响应特性进行研究。设卫星总质量为3300kg，离散后m1=1800kg，m2=1500kg，卫星刚度=2×107N/m，模拟自由边界刚度为卫星刚度的1/20，即=1×106N/m。此时，无附加质量的理想条件下模拟自由边界频率为2.76Hz，卫星模态频率为25.01Hz。设附加质量为卫星总质量的0～20%，通过方程(1)进行固有频率的数值计算，得到模拟自由边界不同附加质量条件下的卫星模态频率。

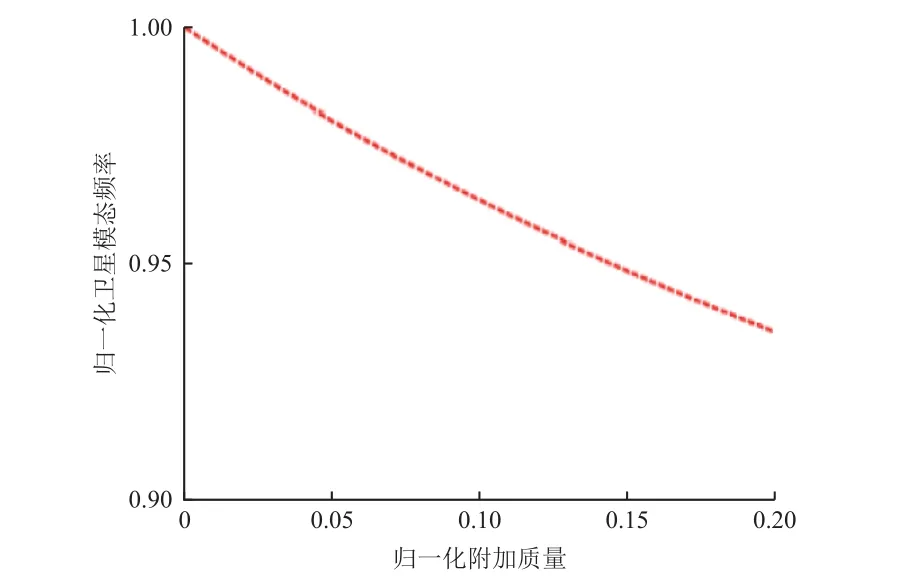
图2 卫星模态频率随附加质量变化曲线Fig.2 The variation of spacecraft modal frequency against the attached mass

在上施加单位幅值的激振力，按2%、5%和10%三种附加质量，分别计算卫星模拟自由边界条件下的频率响应，并与无附加质量时的频率响应进行对比，得到图3 和表1 所示的结果，图中第一阶峰值为模拟自由边界的共振，第二阶峰值代表卫星结构的共振。

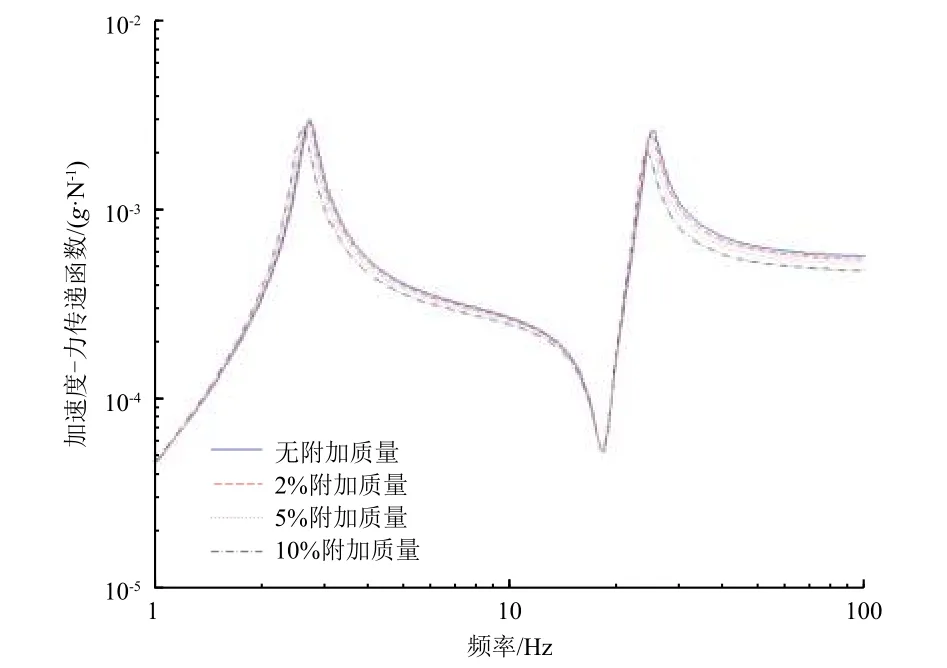
图3 不同附加质量下卫星理论模型的频率响应曲线Fig.3 Frequency response curves of theoretical satellite models with different attached masses

表1 卫星理论模型频率响应特性随附加质量的变化Table 1 The variation of frequency response characteristics of theoretical satellite models against the attached mass

可以看到：当归一化附加质量为2%和5%时，卫星共振频率和共振峰值变化较小，最大分别为2.30%和8.71%；当归一化附加质量为10%时，卫星共振频率和共振峰值变化明显增大，特别是共振峰值的变化达到20.95%，已无法满足工程应用要求。同时通过对比共振频率和共振峰值的变化量可以发现，附加质量对共振峰值的影响程度高于对共振频率的。

1.3 卫星模型仿真验证

某高精度遥感观测卫星结构动力学模型已建立，其自由状态一阶弹性模态频率为16.91Hz。基于该卫星结构动力学模型，利用弹簧单元在卫星端部建立模拟自由边界，前六阶模拟自由边界频率最高1.9Hz；在卫星端部对接框上利用多个集中质量单元建立均匀分布的质量，模拟自由边界物理实现时使用的连接法兰的附加质量。在卫星结构动力学模型的控制力矩陀螺上施加单位幅值的激振力，进行频率响应仿真计算，输出卫星上相机安装平台界面点加速度响应，得到卫星微振动频率响应特性曲线如图4 所示。

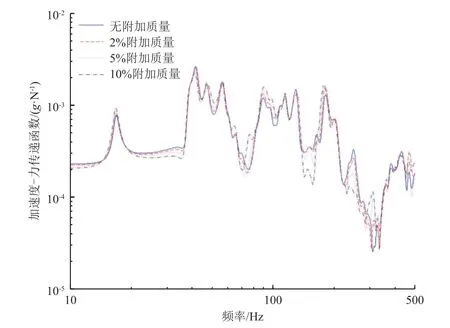
图4 不同附加质量下卫星仿真模型的频率响应曲线Fig.4 Frequency response curves of simulated satellite models with different attached masses

在模型中依次设置无附加质量和整星质量2%、5%、10%三种附加质量，分析验证附加质量对卫星微振动频率响应特性的影响规律。不同附加质量条件下，尽管卫星微振动频率响应曲线形状基本一致，但共振频率和峰值均发生变化，如表2 所示：以无附加质量时的频率响应结果为参考基准，尽管共振频率变化较小，但是当附加质量达到10%时，一阶峰值变化达到20.56%，对卫星动力学特性产生了较大影响。可见，对于附加质量对卫星动力学特性的影响规律，仿真模型与理论模型的分析结果是一致的。

表2 卫星仿真模型频率响应特性随附加质量的变化Table 2 The variation of frequency response characteristics of simulated satellite models against the attached mass

2 实验与分析

2.1 实验设置

通过实验对理论和仿真分析得到的附加质量对卫星结构动力学特性的影响规律进行验证。采用模拟卫星主体结构形式的试验件：主体尺寸为0.6m×0.9m×1.5m（高）；壁板采用铝蜂窝夹层板，内部设置两层隔板；顶板上配置钢质量块以模拟卫星顶部光学相机质量，试验件总质量196kg。利用金属弹簧模拟自由边界，测得模拟自由边界频率为1.89Hz。实验状态如图5 所示。

图5 卫星结构动力学特性验证实验状态Fig.5 Experiment condition for validation of dynamic characteristics of satellite structure

在无附加质量以及2%、5%和10%附加质量4 种工况下，分别进行试验件模态与振动传递特性测试。测试中，试验件各侧板的每个顶点、每条边的中点及板的中心均设置加速度测点，在顶板中心设置1 个测点用以观测模拟相机所在位置的响应，共计57 个测点。利用锤击法获取试验件结构的传递函数，辨识主要模态频率与振型。

2.2 实验结果分析

试验件第一、二阶模态频率见表3，模态振型如图6 所示。根据实验结果，以无附加质量的模态结果为参考基准，随着附加质量的增大，试验件模态频率变化逐渐增大，即附加质量对结构动力学特性的影响逐渐增大。

表3 试验件模态频率随附加质量的变化Table 3 The variation of modal frequency of specimen against the ratio of attached mass

图6 试验件模态振型Fig.6 Modal shapes of the specimen

通过测试中获取卫星微振动扰源模拟安装位置和模拟相机所在位置的振动响应，计算振动传递函数曲线。图7 所示为向激励、向响应的振动传递函数曲线，对应有附加质量的3 种工况，传递函数曲线一阶峰值相对无附加质量工况的变化量分别为2.44%、9.55%和49.35%，可见，10%附加质量严重影响了试验件的结构动力学特性。综合模态频率和频率响应，实验结果给出的附加质量对卫星动力学特性影响的整体规律与理论模型和仿真模型分析结果基本一致。

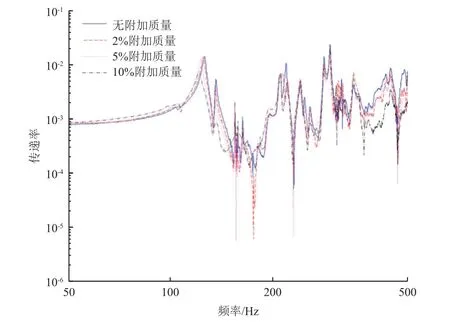
图7 试验件振动传递函数曲线Fig.7 The vibration transfer function of the specimen

进一步利用频响函数相关性的方法对振动传递函数曲线随附加质量的变化进行分析，对、、三个激励方向获取的传递函数曲线相关性进行平均处理发现，随着附加质量的增加，传递函数曲线相关性明显减小（附加质量为2%、5%、10%时，传递函数曲线相关性依次递减为89%、79%、66%），说明附加质量对试验件振动传递特性影响显著。

3 结束语

本文针对微振动试验中自由边界模拟引入附加质量进而影响卫星动力学特性的问题，建立考虑附加质量的自由边界模拟理论模型，并进行了卫星模型仿真和实验测试。根据理论、仿真与实验结果，模拟自由边界附加质量越大，对卫星结构动力学特性的影响越大，故应尽量减小之。而考虑到工程实践，过小的附加质量可能带来实施难题，例如局部连接结构的强度不能满足应用要求，或需要付出较大的代价进行局部连接结构的优化，因此，综合考量后认为应将地面微振动试验中模拟自由边界附加质量控制在卫星总质量的5%以内。此结果可为模拟自由边界附加质量的量化控制提供指导，具有一定的工程应用价值。