工件轮廓线参数计算方法研究
2022-06-27杜珍珍蒋剑军
周 同,杜珍珍,蒋剑军
(1.铜陵职业技术学院基础部,安徽 铜陵 244061;2.铜陵学院数学与计算机学院,安徽 铜陵 244061)
0 引言
工件表面质量直接影响其性能和使用寿命,作为商品也影响客户的使用体验。工件表面是通过工件轮廓线来画像的,所以工件的轮廓线是工件表面质量的外化指标。
工件的轮廓线是通过轮廓仪采集数据后复现的。通过复现轮廓线计算轮廓线的各项参数,工件表面质量由轮廓线的各项参数来描述。
接触式轮廓仪是一种测量工件轮廓线的距离、角度、圆弧半径等参数的两坐标仪器[1],其工作原理是,探针接触到被测工件表面并匀速滑行,传感器感受到被测表面的几何变化,在水平方向和竖直方向分别采样,并转换成电信号(图1)。该电信号经放大等处理,转换成数字信号储存在数据文件中。
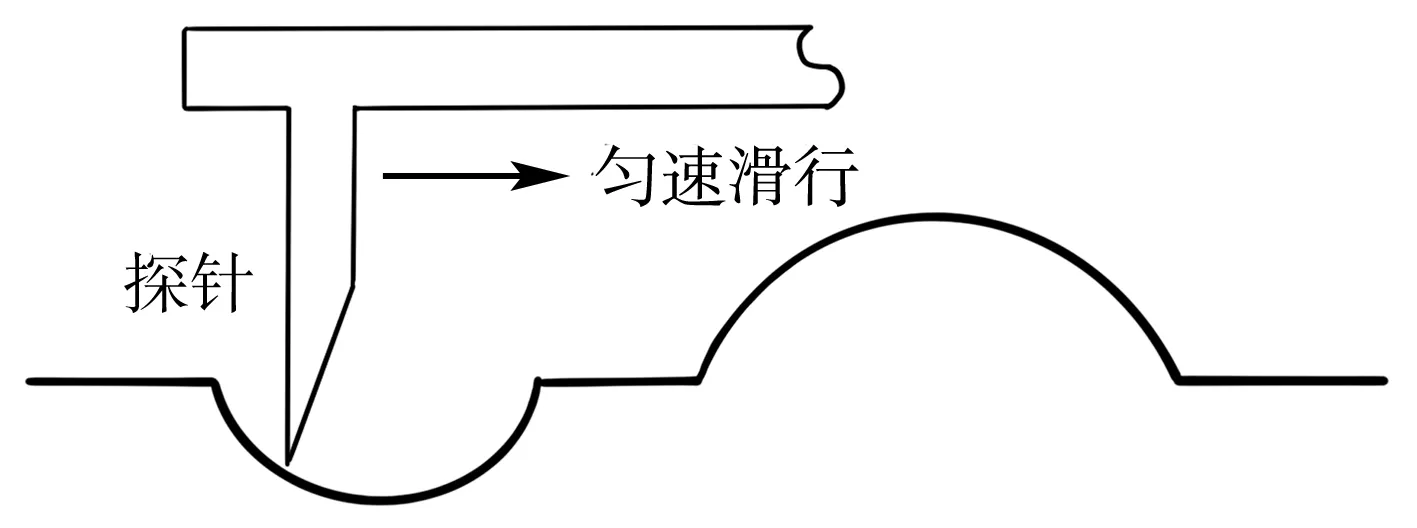
图1 接触式轮廓仪测量示意图
在理想状况下,轮廓曲线应该是光滑的,但由于接触式轮廓仪存在探针沾污、缺陷、扫描位置不准等问题[2],检测到的轮廓曲线一般都呈现出粗糙不平的情况(如图2局部放大图),这给工件轮廓线参数的计算带来误差,从而对工件表面质量的评价带来影响。
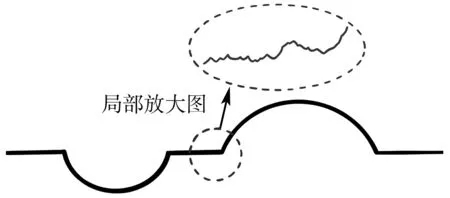
图2 轮廓仪获取的数字信号
为了克服轮廓线数据失真对工件表面质量评价的影响,关于轮廓仪数据校准方法或轮廓线参数计算精度提升方法的研究一直备受关注。范一保等[3]、袁会敬[4]从轮廓仪设计的角度提出提升数据采集精度的方法。王旭刚等[5]、王云飞等[6]通过引入轮廓仪测量新方法解决了轮廓仪测量准确率低和重复性不好的问题。娄云鸽等[7]从轮廓仪的设计和参数的计算两个角度通过测量子午线方法实现了对光学元件轮廓线精密度的评定。张建群等[8]为确保检测数据准确可靠,提出了校准方法及其校准结果的不确定度评定方法,作为接触式轮廓仪的技术依据。
本文在这些成果的基础上研究工件轮廓线数据的校准算法及其各项参数的计算算法设计问题,并应用工件轮廓线公开数据集进行实验以验证算法的有效性。
1 轮廓线标注的基本问题
工件轮廓线公开数据集见全国大学生数学建模竞赛官网(http://www.mcm.edu.cn)。数据集复现轮廓线如图3所示。

图3 工件轮廓线复现曲线
图3中,轮廓线含有三类基本图形:水平直线段、斜线段和圆弧。轮廓线的参数主要是距离、角度、圆弧半径等(表1)[1]。因为计算参数的需要,本文将三类基本图形组合为折线段(由水平直线段与斜线段构成)、直弧线(水平直线段与圆弧的组合曲线)、斜弧线(斜线段与圆弧的组合曲线)、人字形(由两条斜线段构成)。各曲线部分参数如图4、图5、图6所示。

表1 轮廓线的参数
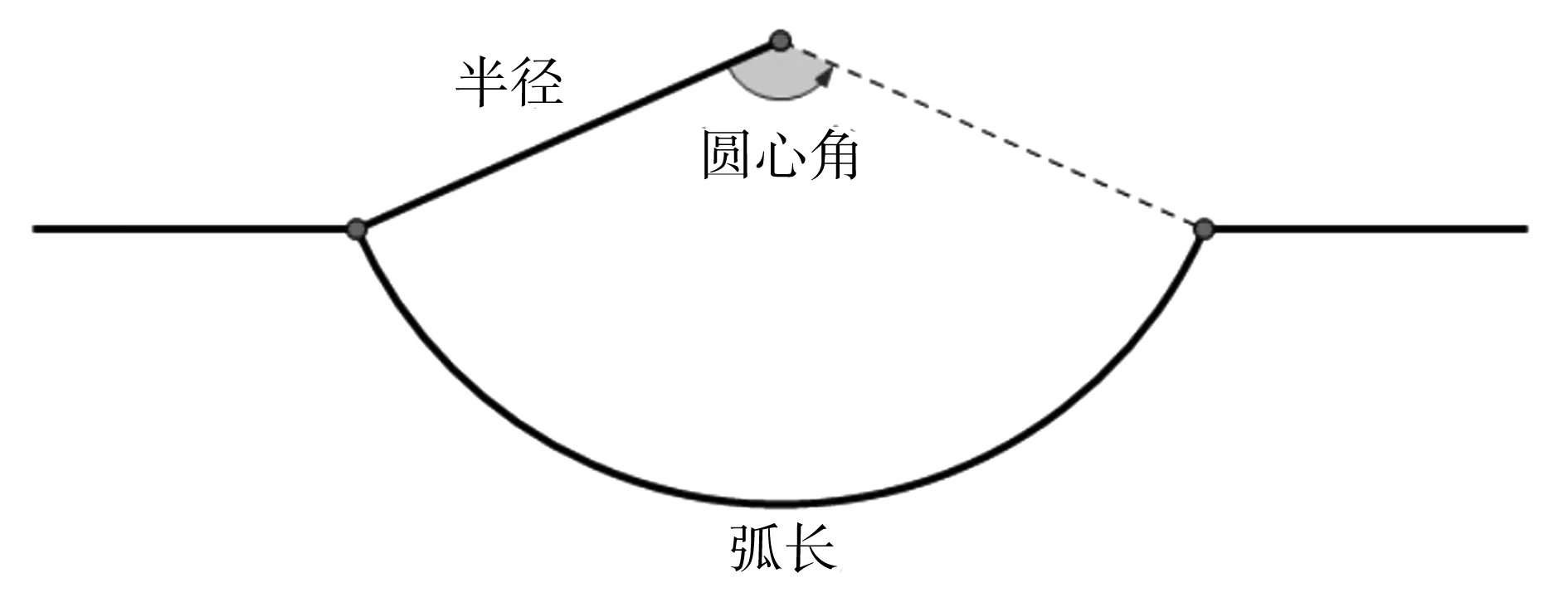
图4 圆弧参数
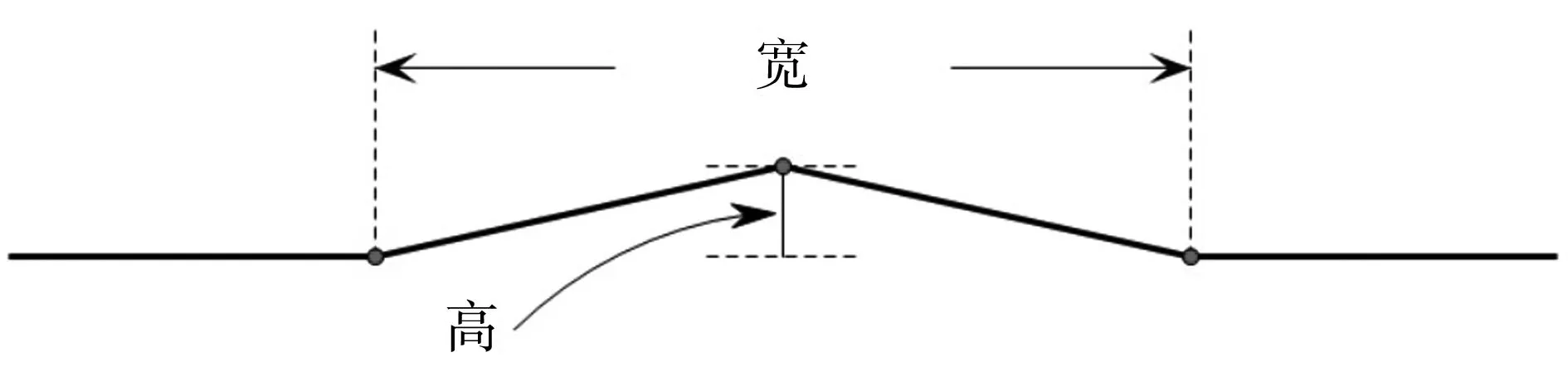
图5 人字形参数
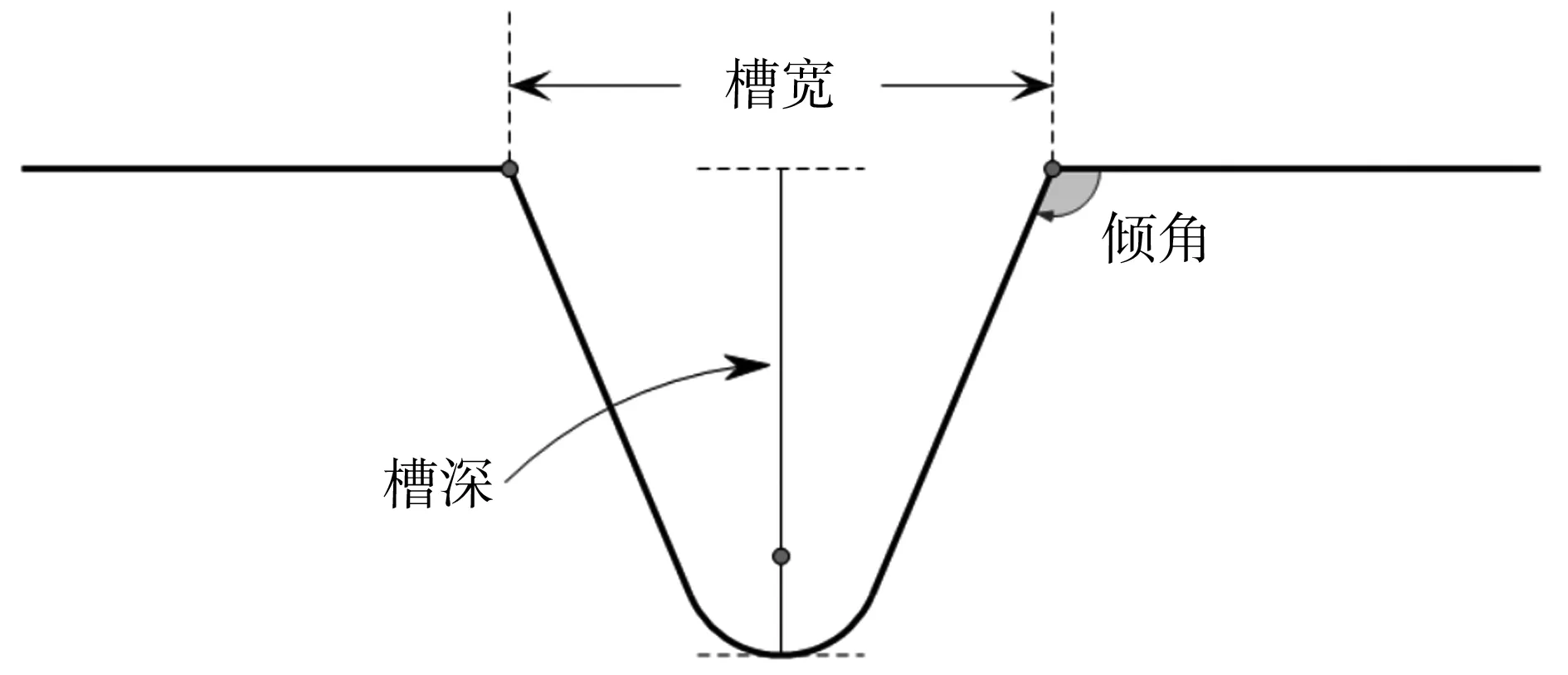
图6 斜圆组合曲线参数
已知轮廓线数据,复现轮廓线以后计算轮廓线的各项参数,这是轮廓线标注的基本问题。本文根据轮廓线数据给出该轮廓线各项参数的计算方法。
2 算法设计
设计轮廓线数据校准及参数计算算法的基本思想是先局部最优逼近,再整体优化调整。在算法描述中使用Matlab的数组语言。
2.1 水平直线段与斜线段之间节点坐标及斜线段方程的计算算法设计
下面介绍图3中第一个折线中节点坐标及斜线段方程的计算算法。图3中第一个折线段如图7所示。设相应于图7的数据为(xi,yi),i=1,2,…,n。如图8所示,在折线段上任取一动点(m,t)。设轮廓线数据中横坐标在[x1,m]上的样本点有p个,在(m,xn]上样本点有q个。
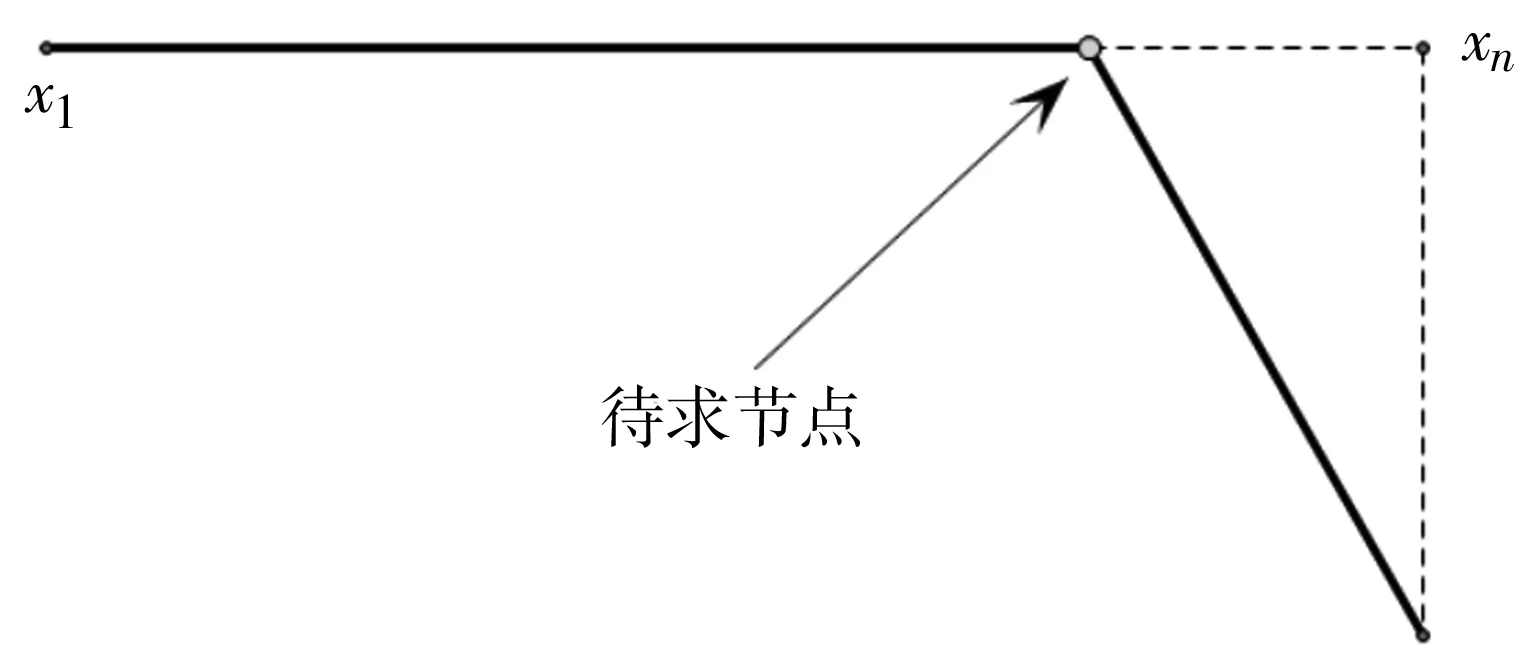
图7 轮廓线上的第一段折线
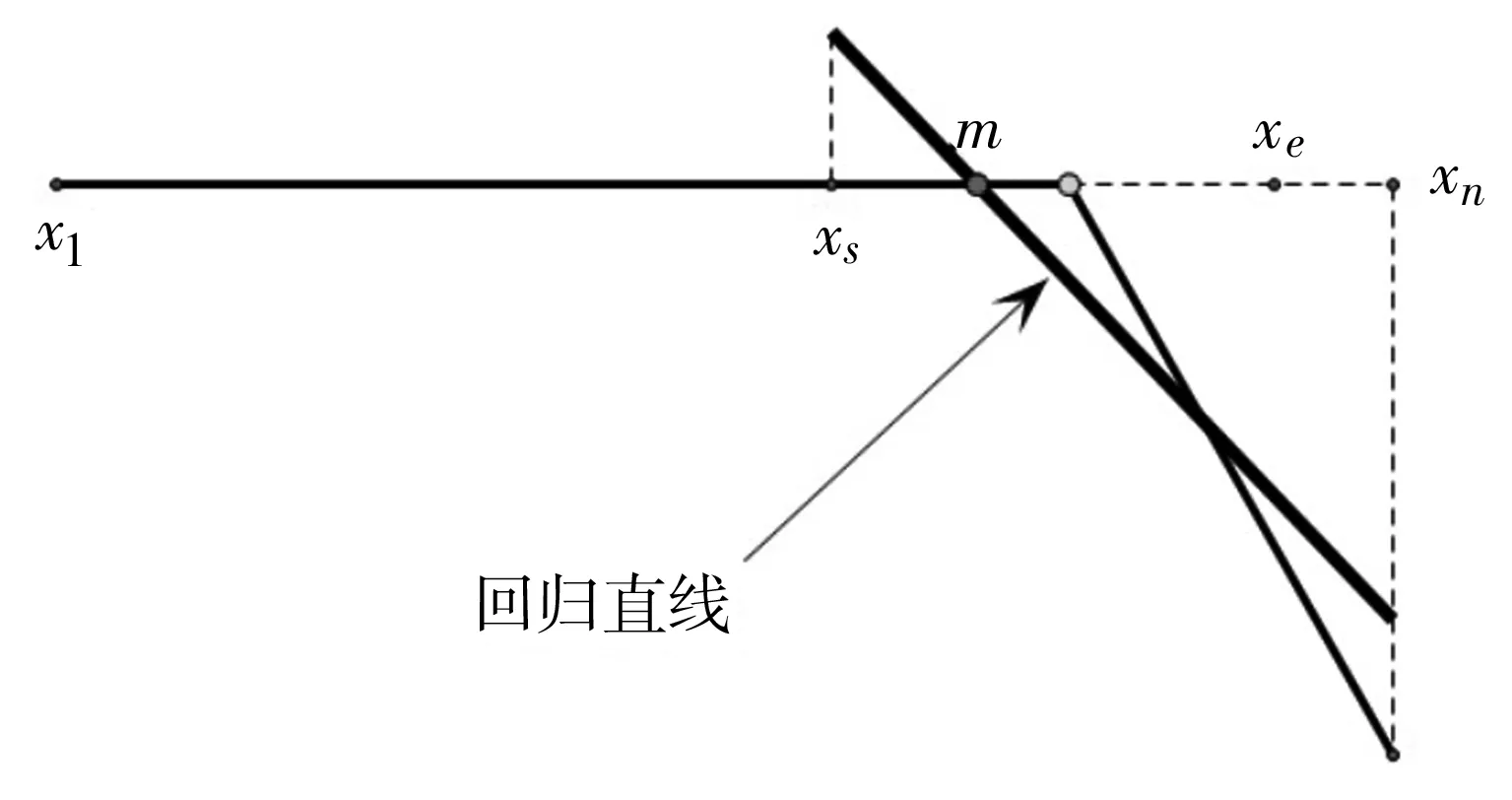
图8 算法1示意图
以(m,t)为节点的近似点,则水平直线段自(x1,y1)至(m,t),斜线段自(m,t)至(xn,yn)。最小误差平方和意义下得水平直线段方程为
(1)
线性回归得斜线段的方程为
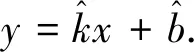
以(m,t)为节点的近似点带来的损失函数取为总误差平方和:
(2)
于是求解节点(xn,yn)的问题,就转化为求位置p使得损失R最小的优化问题。
上述优化问题的决策变量是求和项p,所以这并非常规的优化问题。本文设计该优化问题的求解算法如下:
算法1 斜线段与水平直线段之间节点坐标和斜线段方程的最优逼近算法
1:读入折线段数据;
2:近似:循环变量p=1,2,…,n.
线性回归得斜线段方程,存于数组L中,
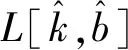
按(2)式计算R(p)
3:计算R最小值所在的位置Ko,输出
最佳逼近点坐标为
斜线段最佳逼近方程为
算法1描述的节点的最优逼近算法与仇谷烽等[9]基于最小二乘法原理提出的可通过测量数据拟合出一个最佳位置放置参数的数学模型明显不同,本文是轮廓线上节点的最佳逼近,而后者是工件放置位置的最佳逼近。
2.2 斜线段与圆弧组合曲线上节点坐标及圆弧方程的逼近算法设计
在轮廓线是光滑的理想状态下,斜线段与圆弧之间的节点是二者的切点。
下面介绍第一个斜圆组合曲线上切点Tl和Tr的坐标、圆弧方程的求解算法。设相应于图9的轮廓线数据为(xi,yi),i=1,2,…,n,其左端点坐标为A(x1,y1),右端点坐标为B(xn,yn),由算法1求得的左右斜线段的斜率和截距分别为[kl,bl]和[kr,br]。相应的算法示意图如图10所示。
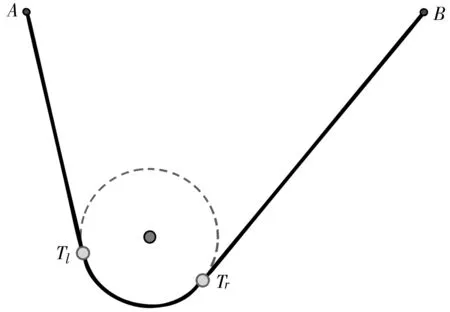
图9 斜弧组合曲线(Tl和Tr是待求切点)
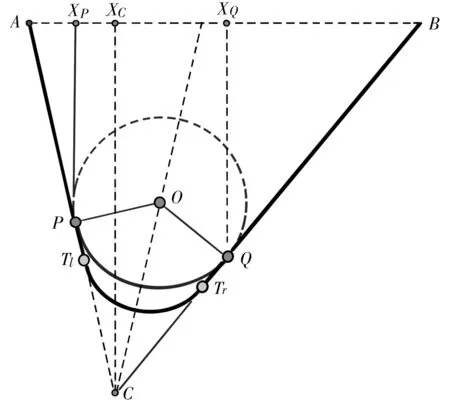
图10 算法2示意图
首先,设左右两端斜线段延长线交点为C(xC,yC),则
(3)
且∠ACB的平分线l的方程为
y=km(x-xC)+yC,
(4)
其中,
(5)
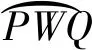
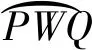
(6)
(7)
点Q的坐标(xQ,yQ)为
(8)
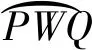
最后最优逼近:设A,P之间的样本数据有p个,P,Q之间的样本点有s个,Q,B之间的样本点有q个,损失函数取为总误差平方和:
(9)
当P在AC上移动时,最小损失对应的点P和点Q分别是切点Tl和Tr的一个理想逼近。于是求切点Tl和Tr的问题就转化为求P的位置p使得损失R最小的优化问题。
算法2 斜弧组合曲线上节点坐标与圆弧方程的最优逼近算法
1:读入数据
斜圆组合曲线数据;
读入算法1中计算得到的斜线段的方程(斜率和截距)[kl,bl]和[kr,br];
2:计算
按(3)式计算点C的坐标;
按(5)式计算角平分线的斜率,按(4)式给出角平分线方程;
A与C之间样本点的个数N;
3:近似:循环变量p=1,2,…,N.
以P(xP,yP)为左切点近似点,然后
按(6)式计算圆心坐标和半径,存于数组A中:
A(p,∶)=[xO,yO,R].
按(7)式计算右切点逼近点Q的坐标,并连同点P的坐标存于数组T中:
T(p,∶)=[xp,yp,xO,yO].
按(8)式计算R(p);
4:计算R最小值所在的位置Ko,输出圆弧的最优逼近方程:
及切点的最优逼近点:
T(Ko,∶)=[xp,yp,xO,yO].
需要说明两点:第一,算法2依赖于算法1的计算结果;第二,与朱晓林等[10]的计算方法相比,算法2保持了曲线的光滑性。
2.3 水平直线段与圆弧之间节点坐标及圆弧方程的逼近算法设计
下面详细介绍第一个圆弧与水平直线段之间节点坐标及圆弧方程的逼近求解算法。
设相应于图11的轮廓线数据为(xi,yi),i=1,2,…,n,其左端点坐标为A(x1,y1),右端点坐标为B(xn,yn),左节点为Nl,右节点为Nr。本文求解Nl,Nr及圆弧方程的算法思想如图12所示。

图11 直弧组合曲线(Nl,Nr是待求节点)
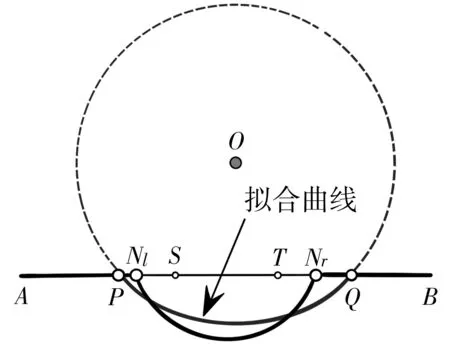
图12 算法3示意图
最后最优逼近:A,P之间的样本数据有p个,P,Q之间的样本数据有s个,Q,B之间的样本数据有q个。假设圆弧的拟合方程为
其中,O(xO,yO)为圆心,R为半径。
由近似所带来的损失取为总误差平方和:
(10)
当P(xP,yP)自A向右移动、Q(xQ,yQ)自B向左移动时对应着一系列损失R(P,Q),其中最小损失对应的P和Q就分别是Nl和Nr的最优逼近,相应的圆弧的拟合方程就是轮廓线圆弧方程的最优逼近。
算法3直弧组合曲线的节点坐标及圆弧方程的最优逼近算法
1:读入数据
直圆组合曲线数据(xi,yi),i=1,2,…,n;
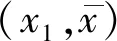
2:初始化:R初始化为J×K零矩阵,用于存储总误差平方和;H初始化为J×K元胞数组,用于存储节点近似坐标和圆弧的近似方程。
3:近似:双重循环
j=1,2,…,J;k=1,2,…,K.
以(xj,yj)近似Nl,
以(xn-k,yn-k)近似Nr,
以横坐标在xj,yn-k之间的数据对圆弧进行非线性回归,得圆心坐标(xO,yO)和半径R;
保存数据:
H{j,k}=[xj,yj,xn-k,yn-k,xO,yO,R].
按(9)式计算损失R(j,k)。
4:计算R最小值所在的位置(Jo,Ko),对应着节点和圆弧方程的最佳逼近:
输出上述最佳逼近结果。
2.4 结果的全局优化调整
上述3个算法着眼于局部最优逼近,且与水平直线段的节点坐标都在轮廓线数据集中,这还不是合理的最优结果。需要对3个算法所得结果进行整体微调。
首先,9条水平直线段方程应该是一致的。
根据上述算法所得水平节点,得到9条水平直线段的样本数据(xik,yik),k=1,2,…,K。由最小二乘法得水平直线段的最优逼近方程为
然后,各斜线段和圆弧与水平直线的交点即为真实节点的最优逼近点。
最后,计算轮廓线的各参数。
3 实验结果
3.1 斜线段与水平直线段之间节点坐标和斜线段方程的最优逼近算法计算结果
8条折线段的节点坐标及斜线段的方程见表2。
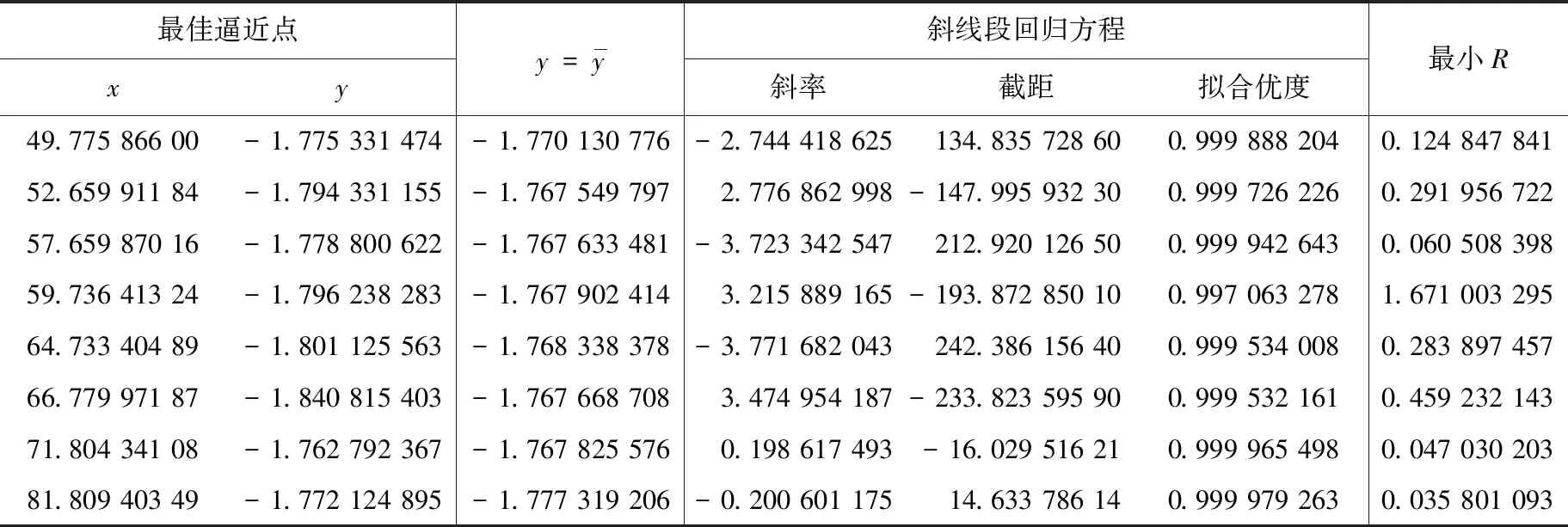
表2 8条折线段的节点坐标及斜线段的方程
轮廓线中第一个折线段的节点结果可视化如图13和图14所示。在图14中,因为算法精度高,拟合数据与原始数据高度重合。图16和图18也是如此。
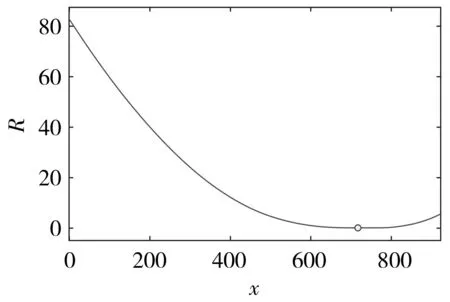
图13 总误差平方和曲线
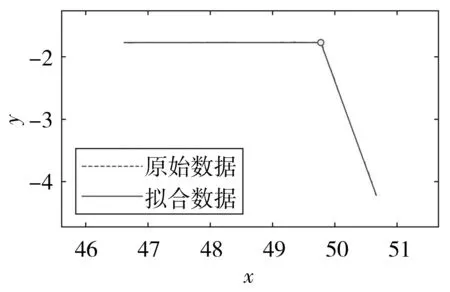
图14 最优逼近效果图
3.2 斜线段与圆弧组合曲线上节点坐标及圆弧方程的逼近算法设计结果
3个斜弧组合曲线的切点及圆弧的最佳逼近如表3所示。
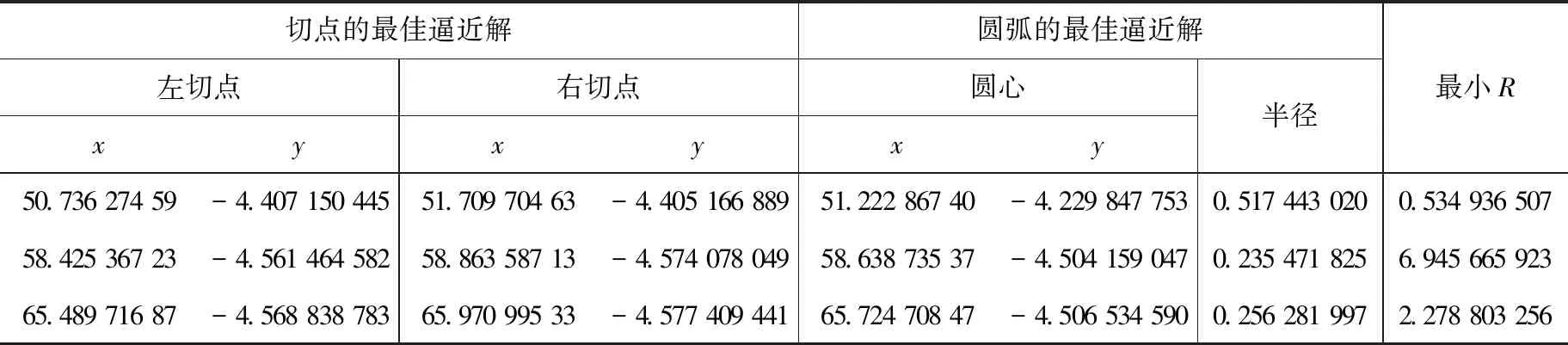
表3 3个斜弧组合曲线的切点及圆弧的最佳逼近
轮廓线中第一个斜弧组合曲线最优逼近结果的可视化如图15和图16所示。
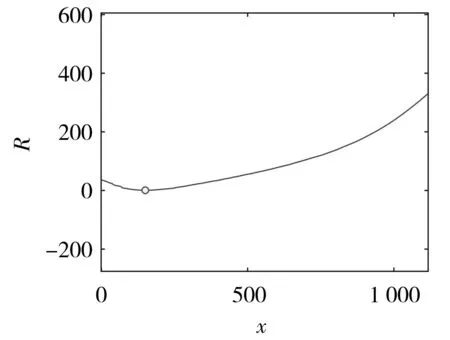
图15 总误差平方和曲线
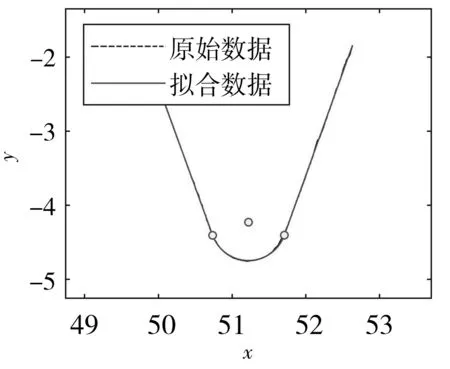
图16 最优逼近效果图
3.3 水平直线段与圆弧之间节点坐标及圆弧方程的最优逼近算法结果
4个直弧组合曲线的节点及圆弧的最佳逼近如表4所示。
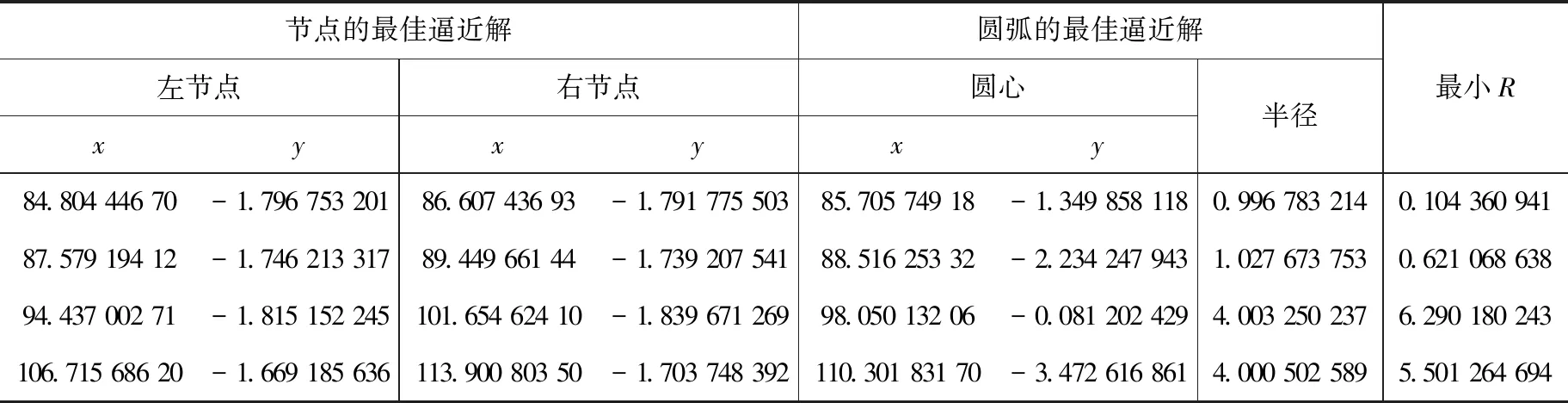
表4 4个直弧组合曲线的节点及圆弧的最佳逼近
轮廓线中第一个直弧组合曲线最优逼近结果的可视化如图17和图18所示。
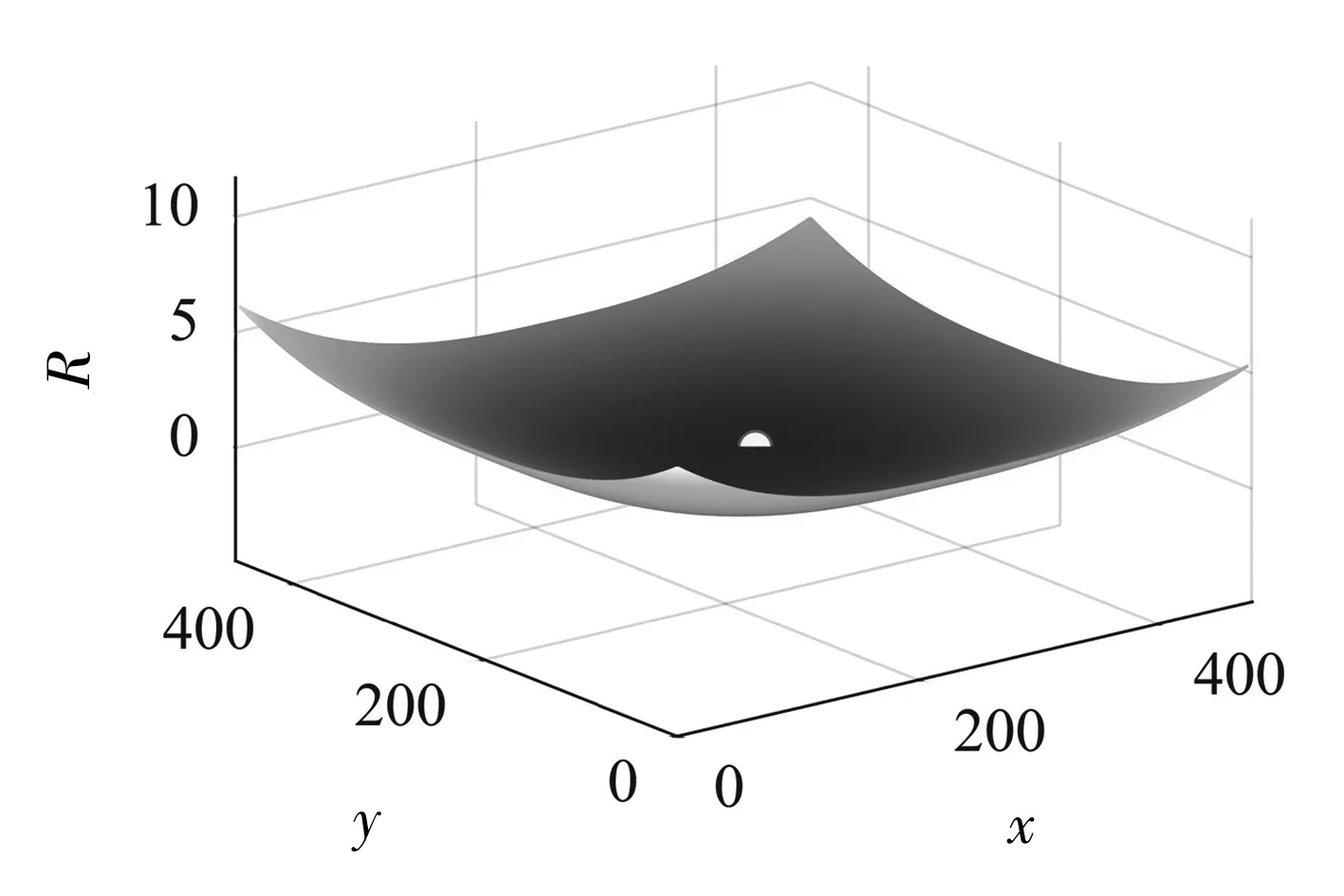
图17 总误差平方和曲面
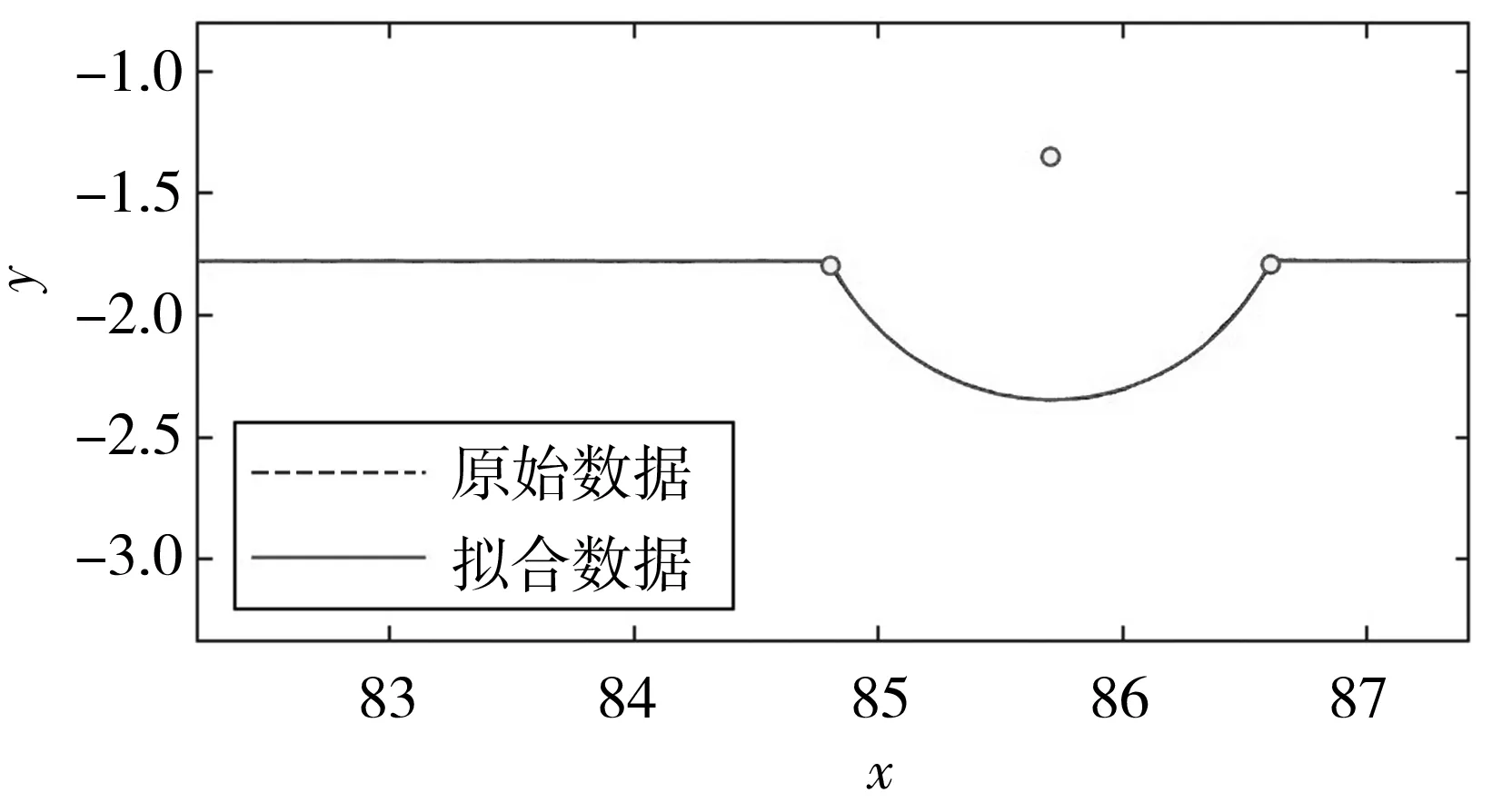
图18 最优逼近效果图
3.4 微调后整体最优逼近结果
水平直线段方程为y=-1.773 808 631。其上各节点的最优逼近点的横坐标如表5所示。
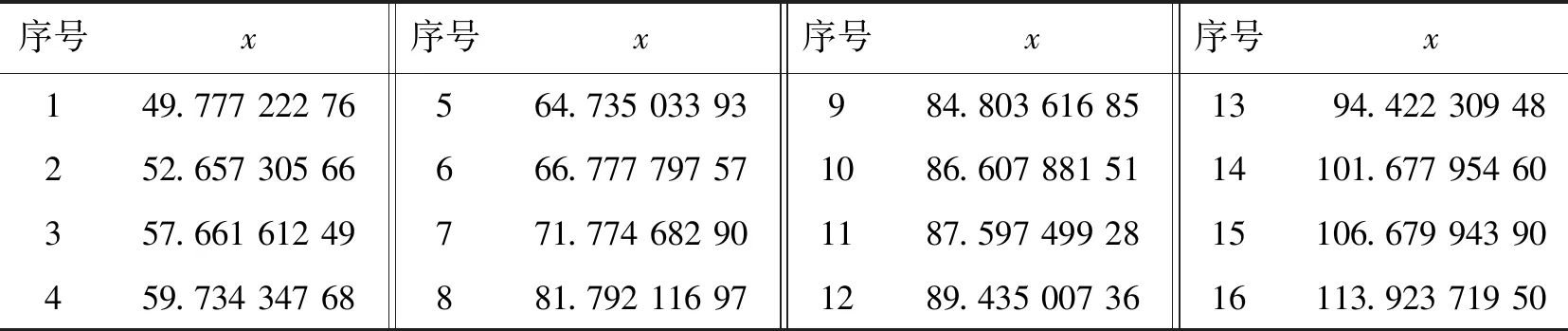
表5 16个节点的横坐标
按校正数据作出轮廓线曲线,如图19所示。此时曲线无论怎么放大都不会再有奇异性。

图19 校正数据绘制的轮廓线
3.5 轮廓线参数的计算
前文第2节主要是对轮廓线失真数据的一个校正,同时计算了部分参数。其他参数可依据校正数据依次计算,结论如表6至表10所示。
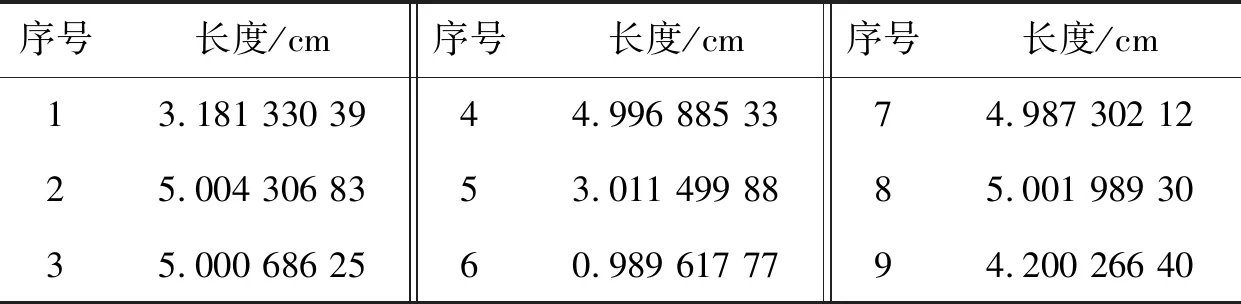
表6 9条水平直线段的长度
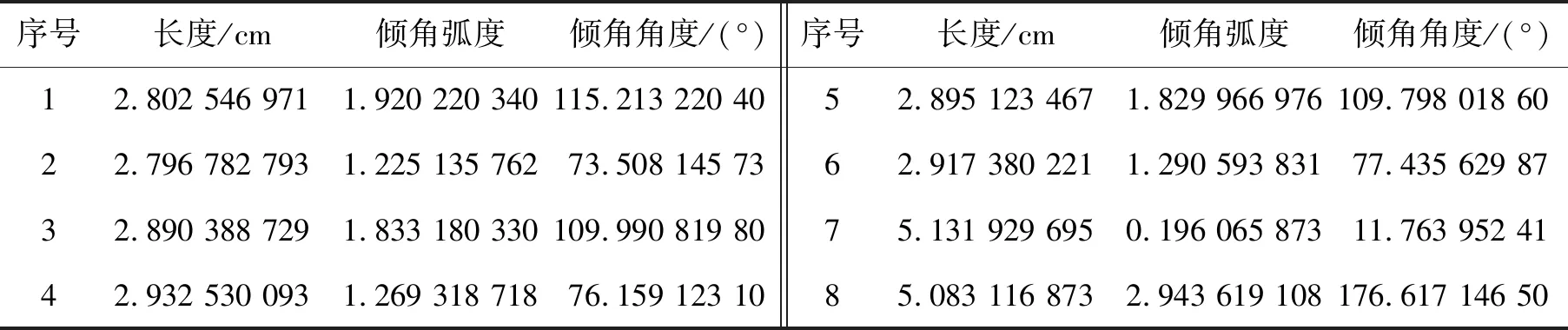
表7 8条斜线段
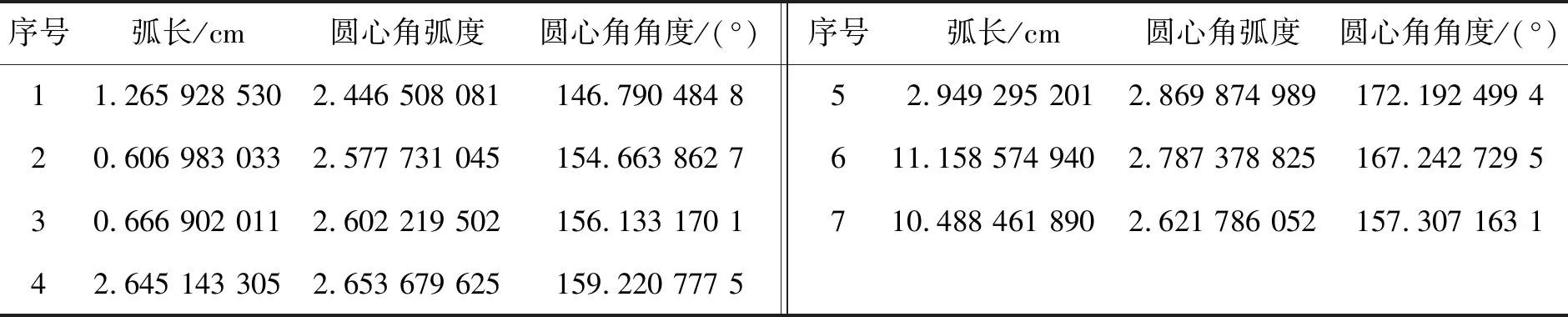
表8 7个圆弧

表9 人字形的参数
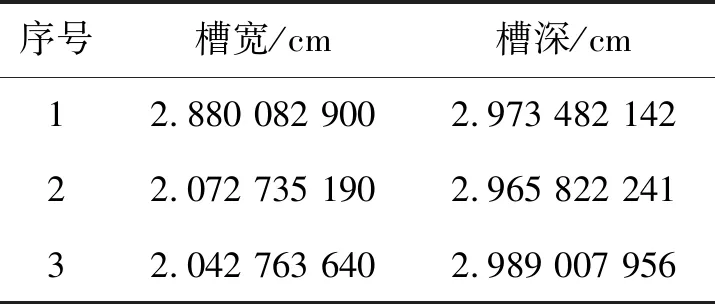
表10 斜弧组合曲线的参数
3.6 实验总结
通过公开数据集对第2节所描述的3个算法进行实验,算法有效性如下:
算法1应用线性回归求解节点优化模型,拟合优度平均达到0.999 453 91,其平均相对误差为 0.043 718%,即通过算法所得最优逼近数据逼近真实数据的程度达99.945 391%,平均相对误差不足0.05%。
算法2和算法3应用非线性回归方法求解轮廓线参数优化模型,平均相对误差分别为0.125 313%和0.091 298%,平均相对误差不及线性回归优良,但都仅在0.1%上下。
图14、图16和图18分别直观展示了算法1、算法2和算法3的最优逼近效果,给出了原始数据和最优逼近数据的比较,二者几乎完全重合。可见,本文提出的轮廓线参数计算的最优逼近算法是有效的。
4 结语
实验结果表明,本文提出的轮廓线数据校准和参数计算算法能有效实现直线段、斜线段以及圆弧等工件轮廓线中常见的二维几何尺寸的自动标注。
本文设计的数据校准和参数计算算法,首先应用线性回归或非线性回归进行局部最优逼近,然后对局部最优逼近结果进行整体优化微调,获得轮廓线参数的全局最优逼近解。与现有结果相比,本文所得结果保证了轮廓线的光滑性。
最优逼近算法容易推广至轮廓线基本图形中含有非圆弧类型[11]曲线的参数计算问题,并能应用于轮廓线异常点的识别[12]。含有非圆弧类型轮廓线参数的标注以及工件发生偏转时轮廓线数据校准和参数计算等问题将是后续研究的内容。
