基于分数阶自抗扰的智能汽车超车轨迹控制
2022-06-27吴贞犇王力超刘丙友
吴贞犇,杨 潘,王力超,刘丙友
(1.安徽工程大学电气工程学院,安徽 芜湖 241000;2.安徽达尔智能控制系统股份有限公司,安徽 芜湖 241000)
0 引言
随着交通运输业的迅猛发展,交通事故频发。由于超车过程复杂,因超车而引发交通事故是最多的状况。为了减少交通事故,目前国内外利用智能控制技术对超车过程进行辅助控制[1-4]。
在车辆自动超车过程中,首先是利用云端技术检测出车辆行驶的环境,然后通过计算到前车的行驶距离,进而规划出一条安全的行驶轨迹,同时计算出所需的偏转角度。针对路径规划主要有JEON等[5]提出的串钉算法、KRISHNAN等[6]提出的最优控制理论、LACAZE等[7]提出的基于搜索算法等。以上算法虽然能计算出超车的曲线,但是对于响应速度和抗干扰能力比较弱。
针对以上的问题,考虑自抗扰技术具有抗干扰、提高响应速度等能力,本文设计分数阶自抗扰对整个超车系统进行控制。针对传统的自抗扰技术对于信号的控制不能满足真实的情况,通过对分数阶理论的应用,设计基于分数阶自抗扰控制的控制系统[8]。传统自抗扰技术具有自解偶能力和不受系统模型的干扰效果,又具备更好的适应现实状况的能力,更加适应对于智能车辆的控制[9-10]。并且加强控制系统的鲁棒性,能够增强汽车反应能力,使汽车的报警速度和刹车反应性能很大程度提升。对于自抗扰参数问题,本文利用模糊控制进行参数整定,减少了系统参数整定问题。同时给出系统的仿真结果,验证了分数自抗扰技术控制车辆的优越性。
1 智能车辆超车系统
1.1 路径规划
直线超车前两车相对运动车速一定,整个过程智能车辆之间的车速趋于不变,且在车道的中心线上行驶,由此建立超车路径规划,如图1所示。

图1 汽车超车路径轨迹图
由图1可知,在a秒后前车A位移D1m,其中,Ra表示当B车超过A车时,两者的运行转角中心距离。考虑碰撞问题,即
(1)
其中,D代表安全距离。
所有转弯半径如下:
(2)
(3)
其中,L3为车宽,L4为车长,L5为平行前进时左轮轮距,D为未超车时车距,D1为超车过程前车行驶距离。驾驶车辆转弯的半径范围为(Rmin,Rmax)。
1.2 运动学模型
在车辆运动中要考虑汽车的运动学模型,通过准确的运动学模型能够真实地反映汽车的运动状况。在汽车准备超车时,汽车后车轮与地面之间满足滚动约束条件,在超车过程中两辆车为相对运动。图2为汽车模型的受力分析图。

图2 汽车模型受力图
在图2中,汽车的三自由度分别代表x轴、y轴和z轴方向转动的自由度,一般用横向速度v、横摆角速度r、侧倾角φ来表示。
汽车三自由度模型的微分方程为
(4)

Yδ=-k1
(5)
(6)

(7)
(8)

Np数值比较小,可以忽略不计,由v=pV可知:
(9)
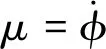
(10)
将此方程组表达成矩阵形式,即:
(11)

标准形式如下:

(12)
其中,A=E-1A,B=E-1B。
利用自抗扰技术自解偶功能,对各个自由度进行控制,协调工作。自抗扰解耦控制框架图如图3所示。利用自抗扰自解偶过程,可以解耦控制前后和侧向移动信息,达到同时工作且互不干扰。

图3 自抗扰解耦控制框架图
2 分数阶自抗扰控制器
控制系统动态响应是研究系统的重要标准,当系统受到干扰时,为了确保系统能保持理想状态,本文利用自抗扰技术来控制智能车的超车行驶轨迹,消除行驶时受到的外界干扰和建模不确定部分带来的影响,确保行驶轨迹的理想化。
2.1 跟踪微分器结构
控制系统中存在动态响应,为了减少系统外部所受干扰,系统响应能够快速恢复到稳定状态,而引入跟踪微分器(TD),解决噪音带来的影响,并得到所需要的提取连续信号和微分信号。提供过渡阶段,实现平滑稳定的变化。
(13)
其中,fhan代表fhan函数,x(t)为理想的轨迹输入信号,v1为对理想轨迹的跟踪信号,v2为v1跟踪信号的微分,r0为跟踪速度因子,h0为滤波因子,h为积分步长。
(14)
跟踪微分器的参数主要取决于r0和h0,当输入为常值1的阶跃信号,且r0=10,h0=0.02时,输出如图4所示。
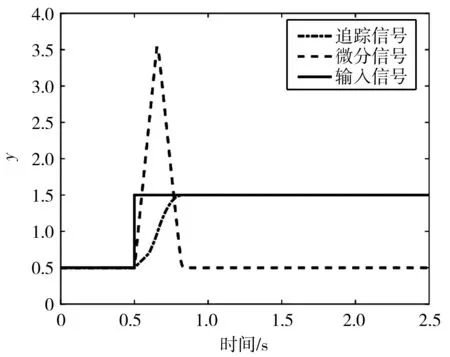
图4 跟踪微分器响应曲线
2.2 改进型状态观测器(PESO)
现实状况基本是分数阶系统,在传统的自抗扰技术的基础上利用分数阶原理进行改进,使整个观测器运行效果更好。具体算法如下:
(15)

(16)
为了验证fnew(·)的优越性,选取σ=0.01和a=0.25,分别与两种传统的非线性函数fan函数和fal函数对比,如图5所示。

图5 非线性函数响应曲线
在图5中,y1为fan函数响应曲线,y2为fal函数响应曲线,y3为本文提出的新型fal函数响应曲线。由图5可以看出,改进型非线性函数具有更好的平滑性和连续性,对状态观测器的控制起到高频抑制作用,增强了观测器的观测效果。
2.3 非线性状态误差状态反馈控制律
非线性状态误差状态反馈控制律(NLSEF)具有消除扰动作用,对于TD传输的信号和反馈的信号进行处理,得到扰动补偿的响应结果,数学表达式如下:
(17)
针对NLSEF双输入单输出的效果,取不同a会导致输出的形状发生变化,而调节σ主要是对非线性函数产生影响,因此可适当调节σ来防止函数的初始位置晃动。
2.4 系统整体框架
根据上述设计方案,建立控制器的系统结构图,如图6所示。
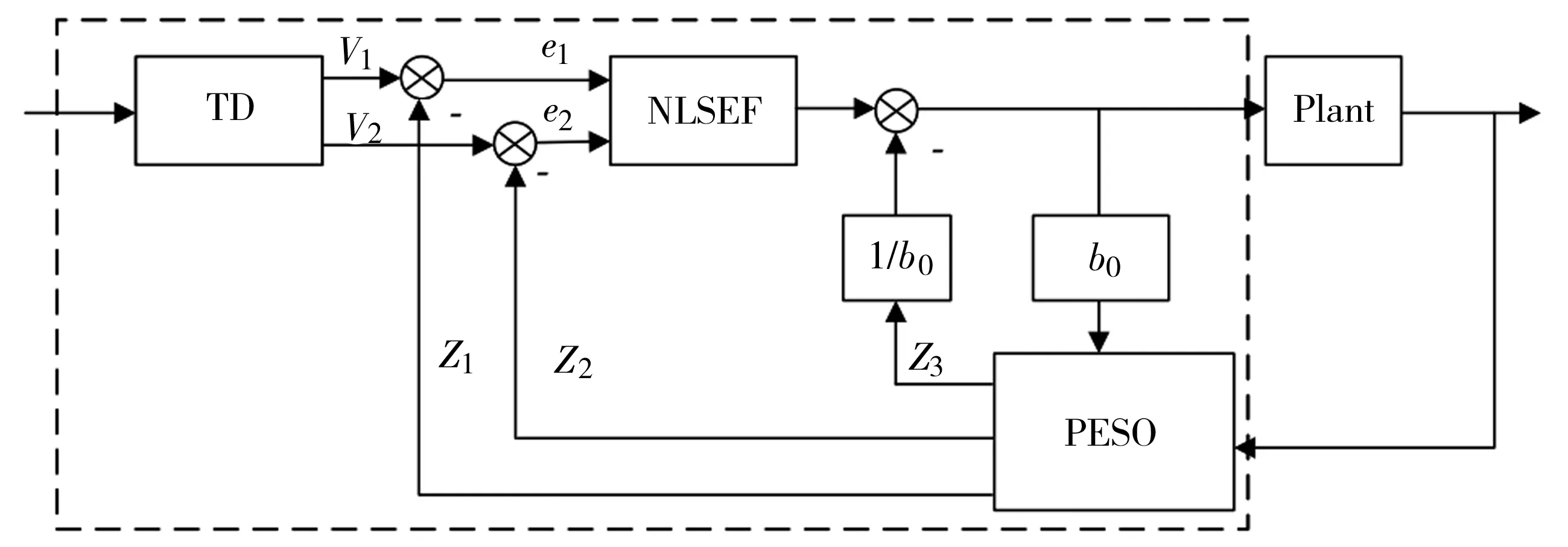
图6 系统框架图
研究对象为汽车的运动学模型,而完整的自抗扰控制器包含跟踪微分器、误差反馈控制率和状态观测器三大模块,能够很好地抑制内外部干扰引起的波动。
3 仿真实验
仿真汽车的系统参数如表1所示。根据表1数据,利用改进的自抗扰器进行仿真,仿真结果如图7所示。数据对比如表2所示。

表1 系统参数

(a)传统自抗扰技术横摆角速度与时间关系曲线 (b)分数阶自抗扰技术横摆角速度与时间关系曲线
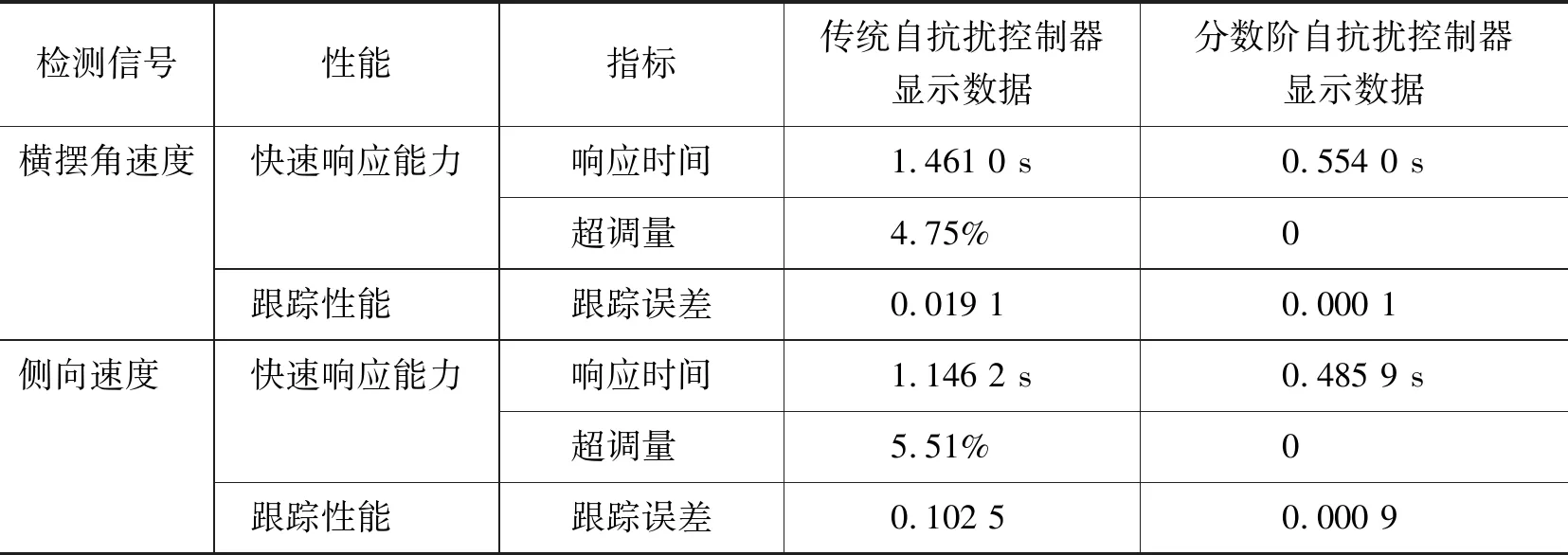
表2 两种控制策略性能比较
通过仿真结果和表2可知,当横向速度恒定为13 m/s时,输入前轮转角角速度为1 rad/s时,利用传统自抗扰技术控制车辆得到的结果如图7(a)(c)所示。图7(b)(d)是利用分数阶自抗扰控制技术控制车辆的响应系统的的响应曲线图,对比可知改进型控制装置响应速度更快,超调量更少。
4 结语
本文设计了基于分数阶自抗扰技术控制的智能汽车的超车系统,采用分数阶控制,提高了汽车超车整个过程中的稳定性、快速性和抗干扰能力,降低了汽车行驶外界干扰和汽车自身的控制复杂性对超车的影响。该系统可实现对智能汽车超车过程中侧向速度和横摆角速度的优化,实现对汽车的高精度、高速度和强稳定控制,满足目前智能汽车超车过程的控制要求。
