基于数据挖掘的门诊辅助知识决策系统的应用研究

刘东丽，袁玉妹，王羡欠

(江西省人民医院，330006，南昌)

0 引言

随着社会的发展，人们对自身的健康越发关注，我国优质医疗资源相对集中，医院面临的就诊压力越发增加，尤其体现在门诊就诊中。此对门诊资源的配置会在很大程度上影响广大患者的就医体验和医院的核心竞争力[1-3]。如何科学、合理并充分地利用门诊资源，成为医院面临的一大挑战[4]。依靠传统的人工门诊资源调配已经无法适应新形势的发展，随着信息技术的发展，借力于信息化技术优化门诊资源配置成为一种新的趋势[5-8]。

数据挖掘(Data mining)又译为资料探勘、数据采矿。它是数据库知识发现(英语：Knowledge-Discovery in Databases，简称：KDD)中的一个步骤[9]。一般是指从大量的数据中通过算法搜索隐藏于其中信息的过程。数据挖掘通常与计算机科学有关，并通过统计、在线分析处理、情报检索、机器学习、专家系统(依靠过去的经验法则)和模式识别等诸多方法来实现上述目标。随着医院信息化的建设不断完善，在功能模块上越来越丰富，数据量也越来越大，如何有效利用现有数据为医疗服务已经成为各个医院不得不面临的问题。为了解决在医学领域具有普遍性的“知识发现”问题，近几年来产生了一项从海量数据中提取知识的技术数据挖掘[10]。国内很多研究尝试将数据挖掘应用于医院信息系统和统计分析与决策中[11-14]，如何在计算机的帮助下，发现隐藏在这些海量数据背后的那些新的有学术价值的医学信息，是系统面临的重大挑战[15-20]。

门诊辅助知识决策系统是一种利用信息化技术和数据挖掘技术，展示一家医院门诊量分布、门诊病种分布、季节性疾病规律、门诊医疗资源配置等综合指标的系统。

本文利用医院现有数据，通过基于数据挖掘的门诊辅助知识决策系统的建立与应用，挖掘门诊患者在就诊时间上的分布情况，掌握门诊患者量高峰时间段，为医院合理安排医护力量和医疗设备提供辅助决策支持，减少患者的等待时间，避免因为医疗资源紧张导致不必要的医疗纠纷；挖掘季度性的门诊患者量增长及季节性疾病情况，找出其特定的规律，为医院在次年相应季度提前建立应对预案提供辅助决策支持，以优化医疗设备，增加相应疾病药品的库存量；挖掘门诊医疗数据，为医院制定最佳的医疗服务举措和最优化的医疗资源配置提供决策支持，增强医院对环境变化的适应性，改善患者就医体验。

1 方法

1.1 数据纳入

某省级三甲综合医院2016—2021年10月门诊医疗数据包含就诊、门诊诊疗数据、门诊人员配备数据。就诊数据包括：就诊序号、日期、付费方式、患者ID号、就诊科室、就诊类别；门诊诊疗数据包括：患者卡号、性别、出生日期、诊断编码、诊断名称、就诊日期。核查数据，剔除性别异常数据59条，剔除出生日期异常数据257条，共纳入数据2 830 770例门诊就诊记录。分析数据，对采集的数据进行分析处理如下(表1)。

表1 研究变量及其量化情况

1.2 统计方法

利用ORACLE数据库存储原始数据，Python3.8进行数据清洗和处理，根据诊断对性别字段空置进行处理。在Python3.8中编写代码对诊断数据进行处理，生成诊断词云图。运用SPSS25工具对数据进行分类、估计、预测、相关性分组或关联规则分析。 运用EViews 进行预测模型建立。

1.3 结果与分析

对2009—2020年10月门诊就诊数据进行描述性统计分析，数据近似正态分布(偏度0.386<1，峰度-0.845<1)，可以用t检验和方差分析，以P<0.05为差异性具有统计学意义。

1.3.1 不同年龄就诊情况 表2可以看出年龄6岁及以下27 227，中位数为344；7—17岁81 244，中位数为993；18—40岁660 726，中位数为8 056；41—65岁1 161 725，中位数为15 329。66岁及以上899 848份，中位数为12 490。采用ANOVA检验，得统计量：F=393.88，P<0.05，即不同年龄组的就诊数量存在统计学差异。

1.3.2 不同性别就诊情况 表3可以看出男性就诊量1 505 449，女性就诊量1 325 321，男:女=1:0.88。男性就诊量的就诊数量中位数为20 341，女性病例为17 483(表3)。通过T检验得到统计量T= 2.585，P=0.663，P>0.05，即不同性别的就诊数据差别没有统计学意义。

表2 不同年龄就诊数量

表3 不同性别就诊统计

1.3.3 诊断分布 诊断数据存在较多自用的编码和名称，为了统计诊断数据的差异性，根据国际疾病分类ICD-10标准编码对诊断数据进行清洗，通过T检验得到统计量T= 5.935，P=0.000，P<0.05，即不同诊断的就诊数量存在统计学差异，通过Python生成诊断词云图(图1)，排名前10的诊断为高血压病、糖尿病、脑梗死、心脏病、腹痛、屈光不正、尿毒症、胃炎、肾移植状态、睡眠障碍。

1.3.4 付费方式 窗口途径1 838 029例，自助途径992 741例，窗口:自助= 1.85:1。窗口途径的就诊数量中位数为25 819，自助途径中位数为13 743(表4)。通过T检验得到统计量T= 7.068，

图1 诊断词云图

P=0.000，P<0.05，即不同途径的就诊数量存在统计学差异。通过分析每年就诊途径数据发现随着信息技术发展自助就诊的数量也在逐年增加。

1.3.5 就诊科室 按科室就诊数量排名前10的为心血管内科、神经内科、内分泌骨质疏松与骨病科、急诊科、消化内科、眼科、骨科、呼吸与危重症医学科、肾脏内科、妇科，通过T检验得到统计量T= 267.315，P=0.000，P<0.05，即不同科室的就诊数量存在统计学差异。

1.3.6 就诊类别 专家就诊579 230例、普通就诊1 989 920 例、急诊就诊169 952例、义诊就诊79 608例、特需就诊12 060例；专家就诊数量中位数为7 828，普通就诊数量中位数为25 497，急诊就诊数量中位数为2 286，义诊就诊数量中位数为2 770，特需就诊数量中位数为102(表5)。采用ANOVA检验，得统计量：F=140.83，P<0.05，即不同类别的就诊数量存在统计学差异。

表4 不同性别就诊数量统计

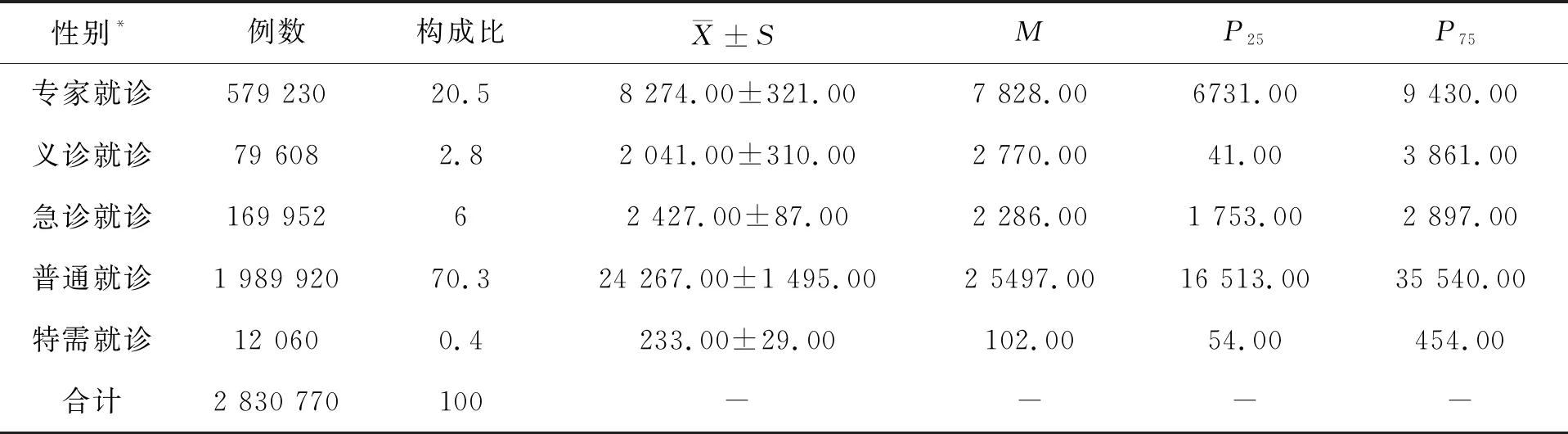
表5 不同性别就诊数量统计

1.3.7 回归分析 单因素分析结果显示，纳入变量中有多个变量在就诊数量组间存在统计学差异，因此需进行回归分析，找出主要影响因素。本研究选用能够反映变量与就诊数量之间直接影响作用的逐步回归模型。

1)变量纳入。因变量为就诊数量，自变量选取影响因素(表1)。通过以上分析可知就诊数量呈偏近似正态分布，对因变量和自变量进行逐步回归分析。变量入选标准为α=0.05，剔除标准为β=0.10。

2)标准化回归方程的建立。从图2中可以看出经过回归后6个变量中只进入了5个变量即X2、X3、X4、X5、X6。根据模型的偏回归系数、标准回归系数、回归系数假设检验t值、P值。建立逐步回归方程如下：

Y=-7.535+5.868X2-6.611X3+3.654X4+0.256X5-0.005X6

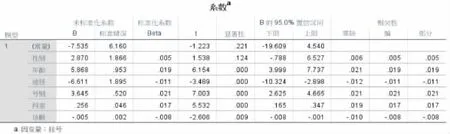
图2 回归分析结果

3)回归方程检验。回归方式检验结果为F=25.254，P<0.05，认为回归方程有统计学意义。从标准化回归方程回归结果可以看出，影响就诊数量的主要因素从大到小为：途径、年龄、就诊类别、科室、诊断。在控制其它因素的条件下，就诊数量与年龄、就诊类别、科室、诊断呈显著正相关，就诊数量与途径呈显著负相关。通过上面分析可以看出，纳入的6个变量中途径、年龄、就诊类别、科室、诊断5个变量对就诊数量存在一定影响，与单因素分析结果一致。

1.3.8 预测模型 选取2016年1月至2021年10月的月门诊就诊数量，进行统计预测建模及分析。共纳入70个月门诊就诊数量作为样本。根据数据特点可进行时间序列建模。

1)平稳性时序图检验。将EXCEL中数据导入Eviews软件中生成时序图，从图3中可以看出门诊就诊数量(ghcount)序列是平稳的。

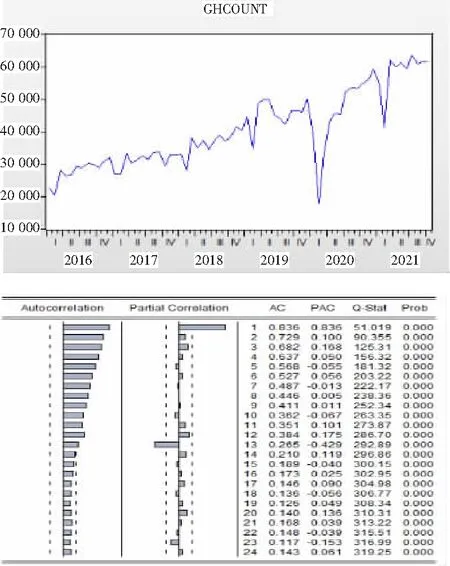
图3 时序和自相关性检验图

样本自相关性检验。从样本相关函数图(图3)可以看到月门诊就诊数量(ghcount)的样本相关函数是缓慢的递减趋于零的，且具有一定。所以，通过月门诊就诊数量(ghcount)的样本相关图，可初步判定该年门诊就诊数量(ghcount)时间序列是平稳。

单位根检验(ADF-Schwarz Info Criterion检验)。对月门诊就诊数量(ghcount)进行ADF检验，结果显示在1%的显著性水平下，单位根统计量ADF=-4.934 538大于Eviews给出的ADF临界值-3.476 275(图4)。所以拒绝原假设，即月人均就诊数量(ghcount)序列是平稳的。

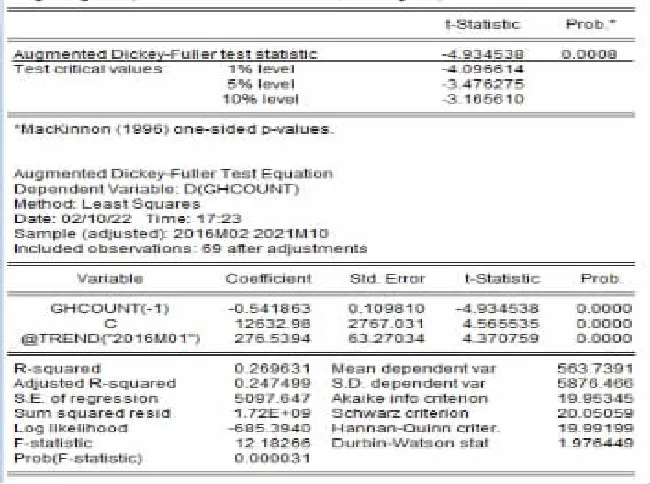
图4 月门诊就诊数量(ghcount)单位根检验

2)估计月门诊就诊数量统计预测模型。从时序图(图3)可以看出，序列既有长期趋势又有周期性，季节性因素会导致统计数据不能客观反映数据变化情况，因此使用Eviews软件中时间序列指数平滑模型exponential smoothing方法对月门诊就诊数量进行调整(图5)，除掉季节波动因素的影响，可初步建立模型ARIMA(1,0,1)×(1,0,1)12和模型ARIMA(1,0,0)×(0,0,1)12。模型检验结果显示：ARIMA(1,0,0)×(0,0,1)12模型的SAR(12)系数、C值系数、MA(1)系数的T检验P值大于0.05，不满足参数有统计学意义要求；模型ARIMA(1,0,1)×(1,0,1)12的SMA(12)系数、AR(1)系数的T检验P值均小于0.05(图6)，满足参数有统计学意义要求。

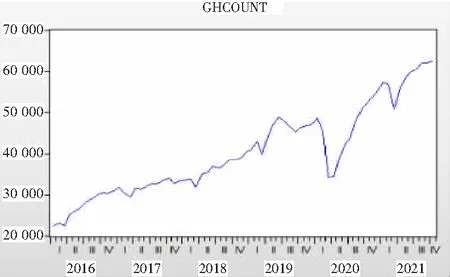
图5 月门诊就诊数量平滑指数处理

3)模型检验。对满足参数有统计学意义的模型ARIMA(1,0,1)12进行残差检验，根据残差相关图可以看出，滞后阶数为10时，Q统计量为10.5，P值为0.389，P>0.05(图7)。因此，可以确定的预测模型为ARIMA(1,0,1)12，其表达式为：

(1-0.966B)▽12▽Xt=(1+0.45B)εt。

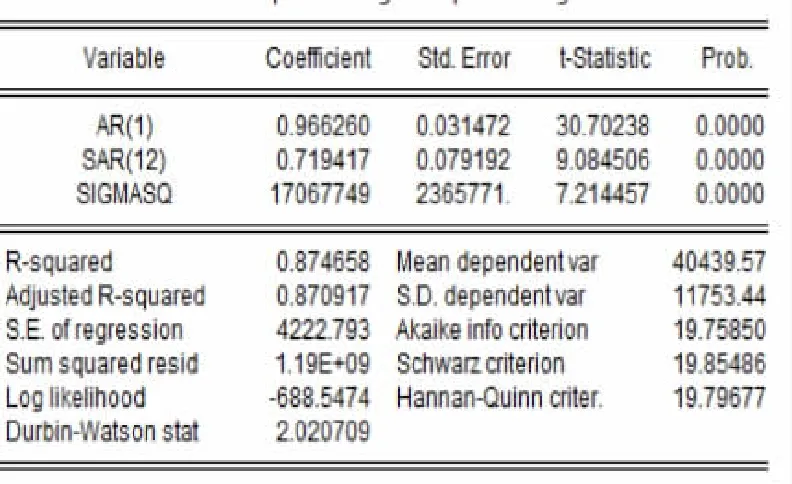
图6 ARIMA(1,0,1)

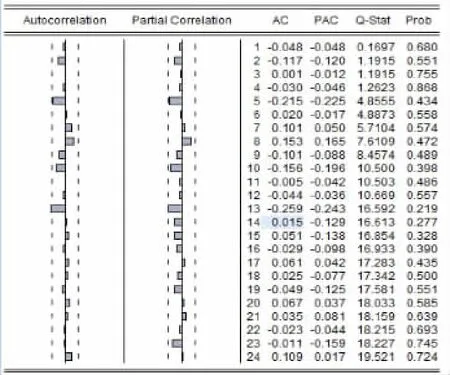
图7 ARIMA(1,0,1)残差检验

Theil′s inequality coefficients表示Theil不相等系数，介于0～1之间；数值越小表明拟合值和真实值之间的差异越小，预测精度越高。covariance proportion 表示协方差误，反映残存非系统预测误差，该误差占比越大，预测效果越好。拟合统计模型ARIMA(1,0,1)，结果显示Theil不相等系数为0.05，其中协方差误为0.969(图8、图9)，大于方差误(0.002 665)，说明模型的预测结果较理想，拟合效果良好，提取序列的信息充分，模型精简。

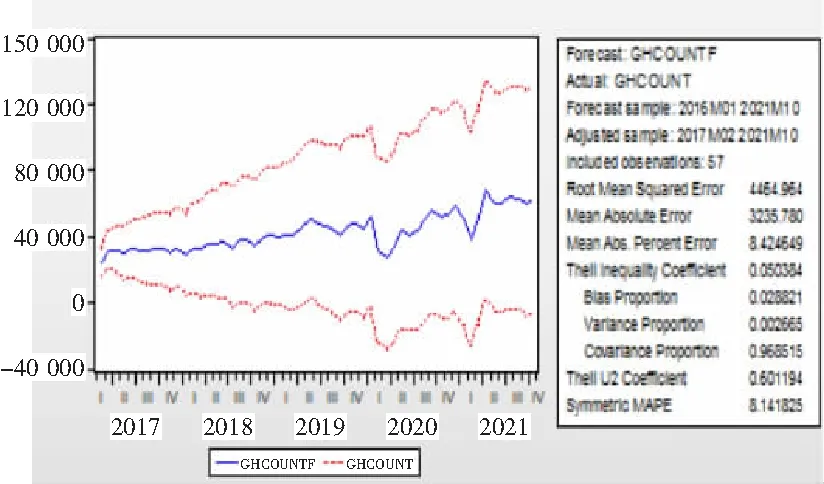
图8 模型预测

4)模型预测。为检验模型的预测误差，现以2016—2020年数据为样本，对2021年1—10月进行预测，并与其真实值进行对比，计算预测误差，误差均值为5.35%(表6)。

图9 模型拟合

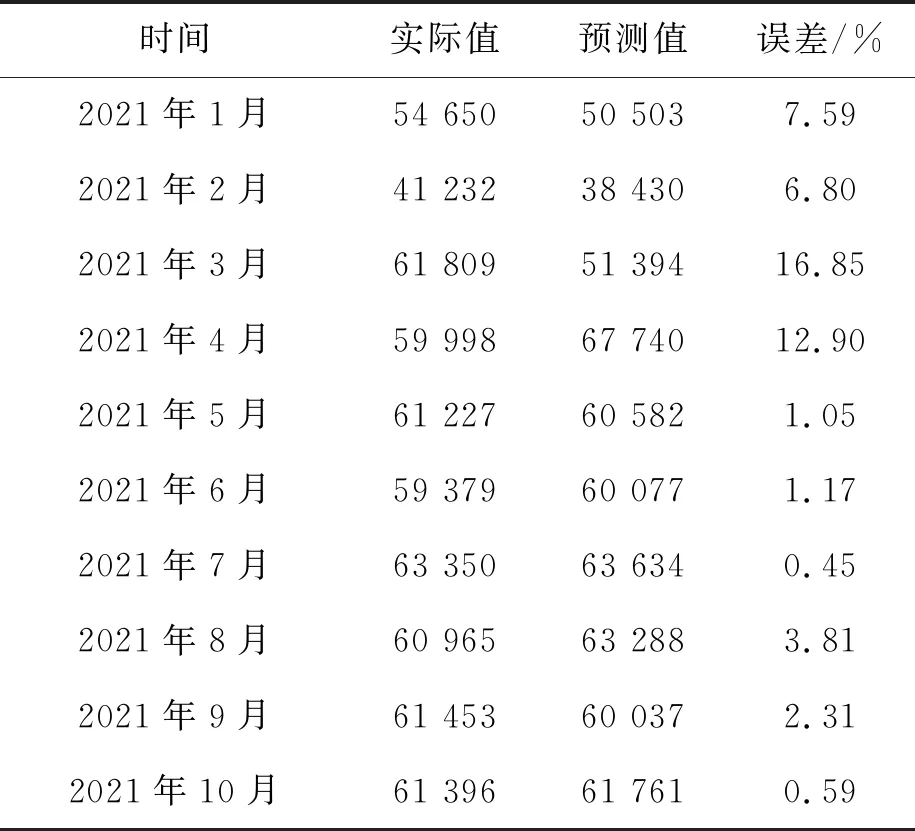
表6 2021年1—10月门诊就诊数量预测

3 结论

通过基于数据挖掘的门诊辅助知识决策系统的建立与应用，挖掘门诊患者在就诊时间上的分布情况，掌握门诊患者量高峰时间段，为医院合理安排医护力量和医疗设备提供辅助决策支持，减少患者的等待时间，避免因为医疗资源紧张导致不必要的医疗纠纷；挖掘季度性的门诊患者量增长及季节性疾病情况，找出其特定的规律，为医院在次年相应季度提前建立应对预案提供辅助决策支持，以优化医疗设备，增加相应疾病药品的库存量；挖掘门诊医疗数据，为医院制定最佳的医疗服务举措和最优化的医疗资源配置提供决策支持，改善患者就医体验。