圆锥型场源瞬变电磁OCCAM反演研究
2022-06-27张富明杨海燕杨夫杰
汪 凌,张富明,杨海燕,张 华,李 哲,杨夫杰
(1. 东华理工大学地球物理与测控技术学院,330013,南昌;2. 山西省煤炭地质物探测绘院,030699,山西,晋中;3. 中国矿业大学资源与地球科学学院,221116,江苏,徐州)
0 引言
我国是世界第一产煤及消费大国,自20世纪以来,我国国民经济增长迅速,对煤炭资源的需求量不断在增加[1]。近年来,时间域电磁探测方法被广泛地应用在工程地质勘察和矿井超前地质预报探测领域中[2]。由于有限环境的限制和目标层(体)深度的不确定性,小回线装置在矿井巷道、工程隧道等地下有限空间及城市和工程浅层探测中通常被采用。该装置通常以共轴形式(中心回线)和共面形式(偶极装置)为主[3-6]。为了增大对地下目标体的探测深度以及探测目标体的响应程度,通常采用增大发射电流或者发射匝数来增强发射磁矩。然而这使得线圈间的互感增大,关断时间变长,浅部“盲区”增大。基于此,在多匝小回线瞬变电磁装置基础上,课题组提出圆锥型场源装置,如图1所示。

图1 圆锥型场源发射装置理论模型图
圆锥型发射场源模型可以近似地表示为由n个半径介于r1和r2之间的单匝线圈组成。如图1所示,单匝线圈内电流强度为I,顶、底部线圈之间的垂直距离为D。各匝线圈的半径及其中心点之间的距离可以分别表示为[7-9]:

(1)
从式(1)中可以看出,ri只受到圆锥型装置顶底半径r1和r2和装置匝数n的约束。
经研究结果表明,圆锥型场源装置的关断时间和电感系数约为多匝小回线的1/8[10]。通过传统瞬变电磁理论叠加可以得到该装置下的一维层状模型瞬变电磁响应[11-12]。
目前,关于圆锥型场源瞬变电磁反演方法研究较少,主要以“烟圈”快速成像方法为主。该方法是一种半定量定性的成像方法,不需要初始模型代入计算[13-14]。近年来,许多研究学者将其他领域的反演方法运用于圆锥型场源瞬变电磁反演方法上。其中包括基于最小二乘改进的“烟圈”反演法、遗传算法、粒子群优化算法等[15-16]。OCCAM反演方法以其平滑模型思想的优势性被广泛应用于各种勘探方法,包括大地电磁法、CSAMT等[17-18]。基于此,本文将OCCAM反演方法应用于圆锥型场源瞬变电磁法反演中。通过本文研究工作,期望获得适用于圆锥型场源的反演算法,丰富圆锥型场源的理论基础。
1 OCCAM反演基本原理
1987年,Constable等人首先提出了OCCAM反演理论。若反演想取得最优解,则反演最终模型应该尽可能简单、光滑,模型粗糙度应尽可能小[19]。OCCAM反演方法原理简述如下。
定义一个粗糙度,粗糙度可以表示为:

(2)
式中m为模型电性参数,一般为电阻率或是电阻率对数。
本文采用矩阵形式进行表示为:
R1=‖∂m‖2
(3)
式中∂是N×N的矩阵,定义为:

(4)
正演模型的响应表示如下:
dj=Fj[m],j=1,2,...,M
(5)
则目标函数的拟合差可写为:
X2=‖Wd-WF[m]‖2
(6)
式中:W=diag{1/σ1,1/σ2,...,1/σm}。
在此基础上,引入拉格朗日乘子μ-1,构成目标函数:
(7)

在反演迭代过程中,为使目标函数取最小,通常令∇mU等于零,则等式(7)可以写成下列形式:
μ-1(WJ)TWJm-μ-1(WJ)TWd+∂T∂m=0
(8)
式中J是M×N阶的雅可比矩阵:
J=∇mF
(9)
假设第k次迭代已完成,定义向量:
mK+1(μ)=[μ∂T∂(WJK)TWJK]-1(WJK)TWdK
(10)
用一系列μ值计算模型mK+1(μ)的真正拟合差:
Xk+1(μ)=‖Wd-WF[mk+1(μ)]‖
(11)
最终找到一个μ值相对最小,拟合差相对最小,光滑度相对高的模型,即是反演最终结果。
Occam反演方法反演流程如图2。
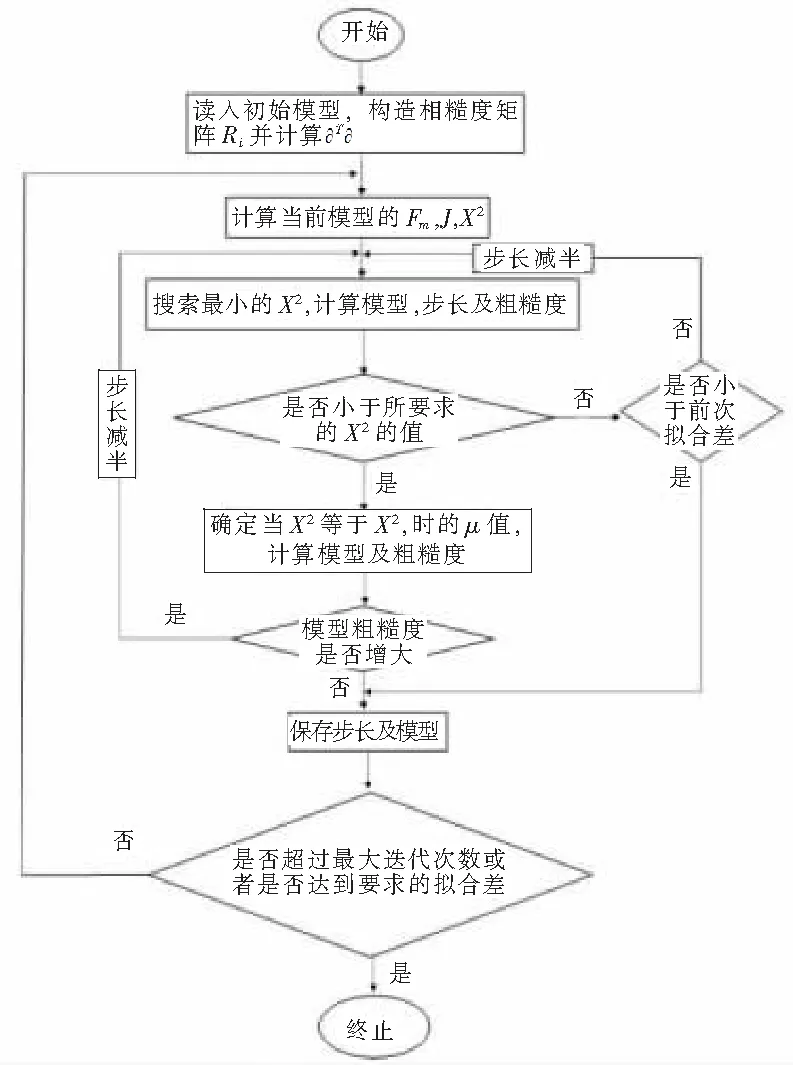
图2 反演流程图
2 理论模型算例
2.1 一维层状介质模型
层状地电模型更能检验反演算法的有效性,因此分别建立3层(H型和K型)以及4层(KH型)地电模型(见表1)。发射电流为10 A,圆锥顶底半径分别为0.5 m和1 m,接收面积为1 m2,匝数为 11。

表1 模型参数表
OCCAM反演的初始模型选择均匀半空间,电阻率取响应的平均值,模型的初始厚度为4 m,增加比例为1.1,一共30层。初始拉格朗日乘子设为0.5,拟合差阈值设为5%,迭代次数设为20次。计算结果见图3、图4、图5。

(a)反演曲线;(b)反演结果的正演响应拟合曲线

(a)反演曲线;(b)反演结果的正演响应拟合曲线
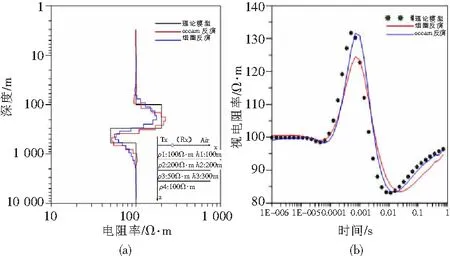
(a)反演曲线;(b)反演结果的正演响应拟合曲线
为了验证本方法不依赖初始模型,分别采用不同初始电阻率(1 Ω·m和50 Ω·m)对同一数据进行反演,反演结果如图6所示。
从图3~图6反演结果可以看出:1)OCCAM反演电阻率更接近各层介质的真实电阻率,反演效果较好;2)OCCAM反演深度更接近层界面,对目标层的底界面分辨能力更强,分层效果更加明显;3)该方法不依赖初始模型,结果准确。由于初始设置的反演迭代次数为20,在实际情况中,当迭代次数为5次时,就会到达误差阈值,反演所需时间较少,故反演效率高。

图6 不同初始电阻率反演结果对比图
2.2 拟二维反演
建立如图7所示的二维理论模型,设置31个测点,点距为10 m,发射电流为10 A,圆锥型场源顶底半径分别为0.5 m和1 m,接收面积为1 m2,匝数为11。将正演计算数据进行OCCAM反演,反演结果如图8所示。

图7 拟二维理论模型图

图8 拟二维反演结果图
从图8中可以清晰看出,OCCAM反演方法在拟二维模型中,反演结果与实际模型对应较好,结果较为准确,进一步证明该方法的有效性和可行性。
3 实测数据反演
采用圆锥型场源装置在东北新肇某地区开展了瞬变电磁剖面实验。实验设备采用澳大利亚生产的Terra TEM瞬变电磁系统,发射电流为8 A,发基频为50 Hz,采样时间为1.687—433.487 ms,叠加次数为32次。圆锥型发射场源顶、底半径分别为0.15 m 和0.325 m,高为0.5 m,绕制127 匝,接收线圈有效面积为13.448 m2。由于处于平原地区,地形起伏的影响可以忽略不计,又前文验证了不依赖初始模型,故初始模型的建立不影响结果,反演深度控制在250 m内。
为了验证OCCAM反演方法的实际效果,将瞬变电磁法反演结果与CSAMT方法进行对比。如图9所示,其中图9(a)表示CSAMT反演结果,图9(b)表示圆锥型场源瞬变电磁反演结果。图9(b)为一段长650 m的剖面反演断面图,对应图9(a)中蓝色虚线框的位置。
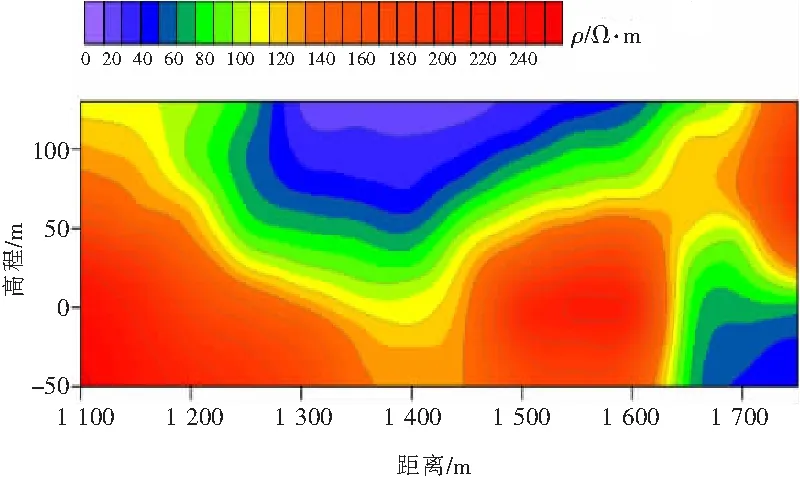
(b)OCCAM反演
从图9中可以看出,经过OCCAM反演方法处理得到的瞬变电磁法反演结果与CSAMT反演结果大概一致,地层电阻率差异特征明显,说明该方法在实测数据处理是可行的。研究内容为圆锥型场源瞬变电磁法数据处理提供新的方法和技术。
4 结论
1)圆锥形场源装置可以等效为不同半径不同高度线圈叠加而成,其正演响应理论可以等效为不同场源半径的中心回线瞬变电磁响应叠加得到。最终通过140点汉克尔变换和250点余弦变换推导出正演响应。
2)OCCAM反演方法不依赖初始模型选择,反演结果更接近地层模型的真实电阻率。
3)OCCAM反演方法分层效果明显。经过实测数据处理表明,该方法可以作为圆锥型场源瞬变电磁反演方法的新手段。
致谢:重庆大学电气工程学院徐正玉博士对文中算法设计提供了帮助!
