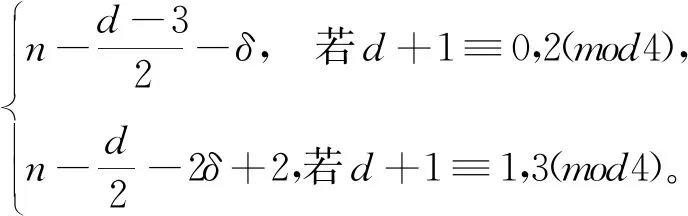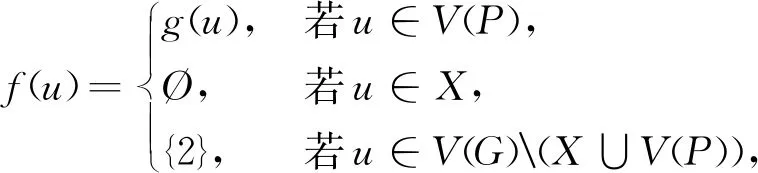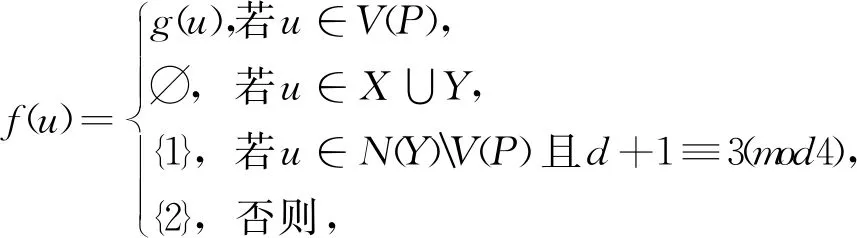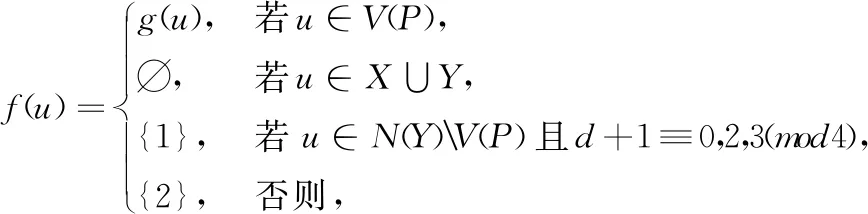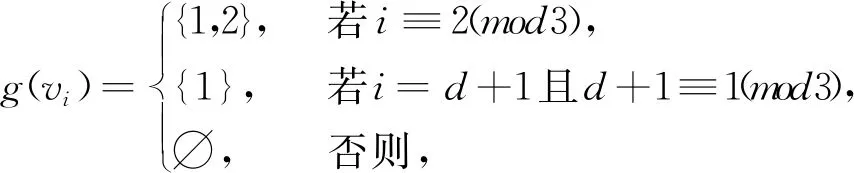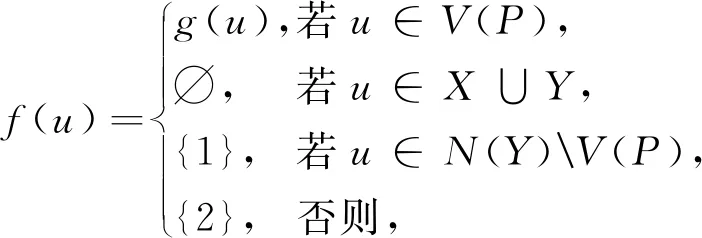图的全局2-彩虹控制数的上界
2022-06-27曾淑婷郝国亮
曾淑婷,郝国亮
(东华理工大学理学院,330013,南昌)
1 预备知识
随着科学技术和实际问题的发展,图的控制理论的内容越来越丰富,具有越来越广泛的应用[1-2]。基于不同的实际背景和历史背景,图的控制数衍生出许多新的控制参数[3-7]。图的彩虹控制问题最早是在2005年被提出的[8],由于确定一般图的彩虹控制数是NP完全的[9],为此,许多学者着重研究图的彩虹控制数的界或特殊图的彩虹控制数的精确值[10-11]。Alqesmah等给出了完全图、完全二部图和轮图的全局彩虹控制数的精确值,并刻画了全局彩虹控制数等于顶点数的连通图[12]。Amjadi等探究了图的全局彩虹控制数的上下界[13]。本文将根据图的直径、最小度和围长等研究图的全局2-彩虹控制数的上界。
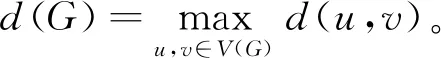
2 主要结果
首先给出Alqesmah等[12]得到的关于路的全局2-彩虹控制数的如下结果,这将在后续证明中多次使用。
引理1[12]: 设P=v1v2…vd+1是含有d+1个顶点的路(d≥5),则γgr2(P)=⎣(d+1)/2」+1且存在一个γgr2(P)-函数g:V(P)→2{1,2},使得
其中:当d+1≡1,3(mod4)时,X={i|i≡3(mod4)且i≤d+1};当d+1≡0,2(mod4)时,X={i|i≡3(mod4)且i 下面给出直径至少为5的图的全局2-彩虹控制数的上界。 定理1:设G是阶为n的连通图且d=d(G)≥5,则 γgr2(G)≤n-「(d+1)/2⎤+1。 证明:设P=v1v2…vd+1是图G的一条直径路且设g:V(P)→2{1,2}是如引理1所示的γgr2(P)-函数,则由引理1知,ω(g)=γgr2(P)=⎣(d+1)/2」+1。定义图G的一个全局2-彩虹控制函数f:V(G)→2{1,2}使得当v∈V(P)时,f(v)=g(v)且当v∈V(G)V(P)时,f(v)={1}。因此 γgr2(G)≤ω(f)=ω(g)+|V(G)V(P)|=⎣(d+1)/2」+1+(n-(d+1))=n-「(d+1)/2⎤+1。 为改进定理1的上界,下面考虑最小度至少为2和围长至少为4的图。 定理2:设G是阶为n的连通图且d=d(G)≥5,δ=δ(G)≥2,g(G)≥4,则 证明:设P=v1v2…vd+1是图G的一条直径路且设g:V(P)→2{1,2}是如引理1所示的γgr2(P)-函数,则ω(g)=γgr2(P)=⎣(d+1)/2」+1。令X=N(v1)V(P)且Y=N(vd+1)V(P)。 断言1:|X|≥δ-1且|Y|≥δ-1。 断言1的证明:由于P是图G的一条直径路,则N(v1)∩V(P)={v2},又因为δ(G)≥2,所以|X|=|N(v1)V(P)|≥δ-1。同理可得|Y|=|N(vd+1)V(P)|≥δ-1。断言1得证。 断言2:对任意u∈X,u在(V(G)(V(P)∪{u}))∪{v3}中至少有一个邻点。 断言2的证明:因为g(G)≥4,所以对任意u∈X,均有v2∉N(u);又因为P是图G的一条直径路,所以对任意u∈X,v4,v5,…,vd+1∉N(u)。此外,由于δ(G)≥2,则对任意u∈X,u在 断言3:对任意u∈Y,u在(V(G)(V(P)∪{u}))∪{vd-1}中至少有一个邻点。 断言3的证明:类似于断言2的证明可得,断言3成立。 下面分以下2种情形讨论。 情形1:d+1≡0,2(mod4)。 由断言2,不难看出函数f:V(G)→2{1,2}使得 是图G的全局2-彩虹控制函数。因此由断言1知, γgr2(G)≤ω(f)=ω(g)+n-(|V(P)|+|X|)≤⎣(d+1)/2」+1+n-(d+1+δ-1)=(d+1)/2+1+n-d-δ=n-(d-3)/2-δ。 情形2:d+1≡1,3(mod4)。 由于P是图G的一条直径路,则对任意u∈X且v∈Y,有uv∉E(G)且N(u)∩N(v)=∅成立。注意到当d+1≡1(mod4)时,g(vd+1)={1};当d+1≡3(mod4)时,g(vd+1)={2}。故由断言2和断言3知,函数f:V(G)→2{1,2}使得 是图G的全局2-彩虹控制函数。因此由断言1知, γgr2(G)≤ω(f)=ω(g)+n-(|V(P)|+|X|+ |Y|)≤⎣(d+1)/2」+1+n-(d+1+2(δ-1))=d/2+1+n-d+1-2δ=n-d/2-2δ+2。 对于围长至少为5的图,进一步改进定理2的上界。 定理3:设G是阶为n的连通图且d=d(G)≥5,δ=δ(G)≥2,g(G)≥5,则 γgr2(G)≤n-2δ-「(d+1)/2⎤+3。 证明:设P=v1v2…vd+1是图G的一条直径路且设g:V(P)→2{1,2}是如引理1所示的γgr2(P)-函数,则由引理1知,ω(g)=γgr2(P)=⎣(d+1)/2」+1。令X=N(v1)V(P)且Y=N(vd+1)V(P)。类似于定理2中断言1的证明可得|X|≥δ-1且|Y|≥δ-1。类似于定理2中断言2和断言3的证明可得,对任意u∈X∪Y,u在V(G)(V(P)∪{u})中至少有一个邻点。因为P是图G的一条直径路,所以对任意u∈X和v∈Y,均有uv∉E(G)且N(u)∩N(v)=∅成立。注意到当d+1≡1(mod4)时,g(vd+1)={1};当d+1≡0,2,3(mod4)时,g(vd+1)={2},则不难看出函数f:V(G)→2{1,2}使得 是图G的全局2-彩虹控制函数。因此 γgr2(G)≤ω(f)=ω(g)+n-(|V(P)|+|X|+ |Y|)≤⎣(d+1)/2」+1+n-(d+1+2(δ-1))=n-2δ-「(d+1)/2⎤+3。 对于最小度至少为3的图,将部分改进定理3的上界。 定理4:设G是一个阶为n的连通图且d=d(G)≥5,δ=δ(G)≥3,则 γgr2(G)≤n-d+⎣d/3」-(δ-3)「d/3⎤。 证明:设P=v1v2…vd+1是图G的一条直径路。定义P的一个全局2-彩虹控制函数g:V(G)→2{1,2}使得 |N(X)V(P)|=∑u∈X|N(u)V(P)|≥|X|(δ-2)=「d/3⎤(δ-2)。 故不难看出函数f:V(G)→2{1,2}使得 是图G的全局2-彩虹控制函数。因此 γgr2(G)≤ω(f)=ω(g)+n-(|V(P)|+|N(X)V(P)|)≤「d/3⎤+⎣d/3」+1+n-(d+1+「d/3⎤(δ-2))=n-d+⎣d/3」-(δ-3)「d/3⎤。 对于围长至少为7的图,将继续改进定理4的上界。 定理5:设G是阶为n的连通图且d=d(G)≥5,δ=δ(G)≥3,g(G)≥7,则 γgr2(G)≤n-d-δ-(δ-3)⎣(d+1)/2」。 证明:设P=v1v2…vd+1是图G的一条直径路且设g:V(P)→2{1,2}是如引理1所示的γgr2(P)-函数,则由引理1知,ω(g)=γgr2(P)=⎣(d+1)/2」+1。令V1={vi∈V(P)|g(vi)={1}}且V2={vi∈V(P)|g(vi)={2}},则|V1∪V2|=ω(g)=⎣(d+1)/2」+1。因为P是图G的一条直径路且g(G)≥7,所以对于任意u,v∈V1∪V2,N(u)∩N(v)=∅。类似于定理2中断言1的证明可得,|N(v1)V(P)|≥δ-1,|N(vd+1)V(P)|≥δ-1且对任意u∈(V1∪V2){v1,vd+1},|N(u)V(P)|≥δ-2。令X=N(V1)V(P)且Y=N(V2)V(P),于是 |X|+|Y|=|N(v1)V(P)|+|N(vd+1)V(P)|+∑u∈(V1∪V2){v1,vd+1}|N(u)V(P)|≥2(δ-1)+(⎣(d+1)/2」-1)(δ-2)=δ+⎣(d+1)/2」(δ-2)。 由于P是图G的一条直径路且g(G)≥7,则对任意2个顶点u,v∈X∪Y,均有uv∉E(G)且N(u)∩N(v)=∅成立。于是不难看出函数f:V(G)→2{1,2}使得 是图G的全局2-彩虹控制函数。因此 γgr2(G)≤ω(f)=ω(g)+n-(|V(P)|+|X|+ |Y|)≤⎣(d+1)/2」+1+n-(d+1+δ+(d+1)/2」(δ-2))=n-d-δ-(δ-3)⎣(d+1)/2」。 下面利用围长给出图的全局2-彩虹控制数的一个上界。 定理6:设G是阶为n的连通图且g(G)≥6,则 γgr2(G)≤n-「g(G)/2⎤+「g(G)/4⎤-⎣g(G)/4」。 证明:设V(G)={v1,v2,…,vn}且不妨设C=v1v2…vg(G)v1是图G的一个长为g(G)的圈。当g(G)≡0,1,3(mod4)时,令X={i≤g(G)|i≡0,2(mod4)};当g(G)≡2(mod4)时,令X={i 是图G的全局2-彩虹控制函数。因此 γgr2(G)≤ω(f)=n-|X|=n-「g(G)/2⎤+「g(G)/4⎤-⎣g(G)/4」。