一种便捷的远心三维测量系统标定

周鹏许，钟汇凯，伏燕军*，桂 程，钟 声

(1.南昌航空大学无损检测教育部重点实验室，330063，南昌；2.南昌航空大学测试与光电工程学院，330063，南昌)

0 引言

条纹投影轮廓测量法(FPP)因其具有数据采集量大、测量精度高、无接触、便携和灵活等优点成为三维形貌测量中应用最广泛的技术之一。然而随着工业设计变得更加精确和小型化，传统(宏观)的FPP已不能满足越来越高的加工制造标准和要求，微观层面的三维测量已经变得越来越重要。显微条纹投影轮廓测量法(MFPP)通过使用显微光路缩小投影图案和成像尺寸，在小视场内实现了更高精度的三维测量[1]。相比于传统的针孔模型相机，远心相机具有放大倍数恒定和几乎零畸变的优点，非常适用于高精度的成像检测。近年来，基于远心相机的微小物体三维重建方法越来越受到关注[2-3]。然而远心镜头的成像原理为正交投影，待测物体和采集图像之间呈仿射变换，不能用传统针孔相机模型建模，无法利用旋转矩阵内在的正交性提供的约束来获得外参的封闭解，一般需要引入额外的实验操作来辅助求解。

目前有很多关于远心相机的标定方法已被提出[4-11]。Li等[4]提出了一种考虑镜头畸变远心相机精确标定方法，但是该方法在标定前需要知道相机传感器的像素尺寸。在他们之后的工作中使用该方法标定了一套远心FPP系统[5]。然而，该方法在求相机的外部参数时存在旋转矩阵的符号模糊问题。Chen[6]提出了一种新的远心相机标定方法，该方法通过分解单应性矩阵得到相机的内参与外参，并利用微定位平台成功解决了基于平面标定技术的符号模糊问题。Yin等[7]提出使用一般成像模型对远心相机进行标定，获得了较高的标定精度。该方法的缺点是在标定系统的过程中，需要位移台来控制标定板按预设的方式进行移动，增加了整个标定过程和测量系统的复杂度。Rao等[12]提出了一种远心FPP系统的柔性标定方法，该方法假设远心相机的远心度并不是完美的，可以将远心相机的仿射成像模型看成是针孔成像模型的特殊情况，并且用张[13]的相机标定方法标定远心相机的外部参数。然而当使用远心度很好的远心相机时，此方法可能会失效。Yao等[14]提出了一种双侧远心镜头的灵活标定方法，使用一个带有额外已知高度平台的平面标定板，解决了符号模糊问题，但该方法需要特制的标定板。

如上所述，基于二维平面标定板的远心相机标定方法存在外部参数符号模糊问题[15-16]，本文在单应性变换平面标定法的基础上，对双远心三维测量系统提出了一种便捷的标定方法，能够直接获取远心相机的外部参数。通过建立2个间隔一定高度标定板平面之间的面内旋转和平移关系，能够得到标定板平面控制点的三维坐标信息，进而完成外参封闭解的求解。该标定方法仅需要借助一个可以在参考面上任意放置的标准测量块就能完成远心三维测量系统的标定，具有高灵活性和实用性。

1 远心三维重建系统标定方法

1.1 远心相机成像模型

远心相机仿射成像模型可用式(1)表示

(1)

式中：m表示远心成像系统的有效放大倍数；(u0,v0)是畸变中心，一般定为相机成像平面的中心；R和T分别是世界坐标系到相机坐标系的旋转矩阵和平移向量；A和K分别表示远心相机的内参矩阵和外参矩阵；P(XW,YW,ZW)是世界坐标系下控制点的坐标。由于仿射成像模型只涉及到旋转矩阵的前两行，所以R2×3表示旋转矩阵的前两行，T2×1=(tx,ty)表示截短的平移向量。通常将世界坐标系的x-o-y面建立在标定目标平面上，这样每个特征点的Zw坐标为0。由此式(1)可表示为

(2)

其中H是一个3 × 3的单应矩阵，该矩阵用于描述靶标平面点的世界坐标与控制点的像素坐标之间的关系，可以用直接线性变换(DLT)算法求得。

由于镜头制造或安装的原因，镜头畸变总是存在的，远心镜头的畸变主要分为径向畸变、切向畸变和薄棱镜畸变。径向畸变是由于透镜形状不完美引起的，在所有畸变类型中径向畸变占主要成分，因此本文只考虑径向畸变。畸变方程可表示为[9]：

(3)

1.2 放大倍数的标定

由于旋转矩阵是正交的，且旋转矩阵的列向量是单位向量 ，由此可得如下约束关系

r11r12+r21r22+r31r32=0

(4)

(5)

结合式(4)和式(5)，可得

(6)

结合式(2)和式(6)可得

m4+Bm2+C=0

(7)

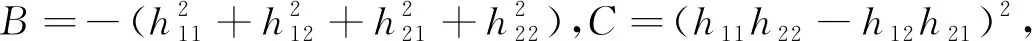
假设畸变中心(u0,v0)的坐标为相机成像面的中心，则截短的平移参量可由式(8)得到

(8)

1.3 外部参数的标定及符号模糊问题

每一个标定板姿态的外部参数一般是不一样的，其旋转矩阵左上角2×2的子矩阵可由H矩阵直接得到。由于旋转矩阵的约束条件RRT=I和det(R)=1，剩下的矩阵元素可由式(9)得到

(9)

r1、r2、r3分别是矩阵R的3个行向量。然而，从公式(9)看出，元素r13和r23存在符号不确定问题。

为了恢复正确的符号，需要知道特征点的高度坐标。在本文中，使用一个已知高度的标准测量块，将平面标定板放置在该标准块上，捕获标定板图像。结合放置之前所拍摄的标定板图像，随后用于确定旋转矩阵。如图(1)所示，由于标准块的2个面平行，所以2个标定板平面也是彼此平行的。

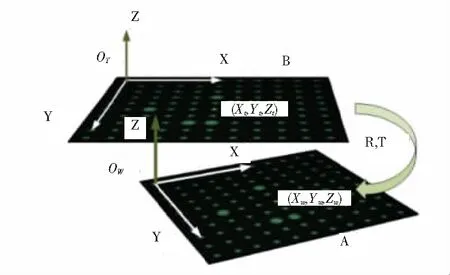
图1 标定板位置关系示意图

分别建立世界坐标系OW(Xw,Yw,Zw)和标定板坐标系OT(Xt,Yt,Zt)在标定板位置A和位置B上。实际上2个标定板平面之间只有绕z坐标轴的旋转，因而对于标定板位置B上的任意一点p(XT,YT,ZT)，有如下关系：

(10)

其中θ表示2个标定板之间的面内旋转角度，(tx,ty,tz)表示2个坐标系之间的平移变换，tz为已知量，即标准块的高度。去掉Z坐标的变换，则式(10)可表示为

(11)

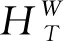
(12)

由式(12)和式(2)可得：

其中HT是标定板在位置B的单映性矩阵。因此坐标系OT中的点(XT,YT,0)的世界坐标为PW(xw,yw,tz)。其中，xw,yw由式(10)得到。根据式(1)，r13和r23的值可由式(13)得到

(13)

r13和r23的值不一定严格满足(4)和(5)的约束条件，但它们的符号被确定。

1.4 参数优化

相机的所有内外参数都需要进一步的优化，使用极大似然估计使标记点的像素坐标与预测像素坐标之间的距离之和最小。这是一个由式(14)表示的非线性优化问题。

(14)

本文使用立体视觉模型来计算世界坐标系下的三维点云[18]。投影仪可以看作是一个逆相机，其工作原理可以用与1.1部分相同的数学模型来描述[19]。因为投影仪不能直接捕捉图像，建立相机像素和投影仪像素之间的精确对应关系，使投影仪也能像相机一样拍摄到图像。本文中使用相移法和多频外差法计算连续相位，通过连续相位来建立相机像素坐标和投影仪像素坐标之间映射关系。对应投影仪中的像素坐标可表示为：

(15)

2 系统装置和三维重建实验

2.1 系统装置

测量系统的远心相机是由分辨率为1 920×1 200的相机MER-131-210U3c和放大倍率为0.37的远心镜头VP-LTCM037-150-S组成。相机的视场范围为13.5(H) mm × 16.5(W) mm。镜头工作距离为150 mm。一个装有远心镜头(型号：VP-LTCM02-180S)的DLP投影仪(DLP LightCrafter 4500，分辨率：1 140×912)用来投影正弦条纹。标定板是一个由9×11白色圆形阵列均匀分布的陶瓷平面板(型号：cc-008-G-0.65)，邻近2个圆的距离为0.65 mm。实验所用标准块厚度为1.01 mm。图2为微小物体测量系统实物示意图。

图2 (a)实验所用标定板；(b)实验系统实物图；(c)实验所用标准块

2.2 标定实验

将标定板摆放在相机和投影仪的共同视场内，对于每一个标定板姿态，将一系列垂直和水平方向的正弦相移条纹图投影到标定板平面上，用相机拍摄一组标定板图片(其中包含12张水平条纹图、12张竖直条纹图和一张255均匀灰度照明的空白图)，然后任意改变标定板姿态，再拍摄另一组。在本次实验中一共拍摄了9组图片。采用四步相移结合三频外差的方法得到连续相位。表1是相机和投影仪的标定参数。

表1 相机和投影仪的内外参数

如图3(a)和3(b)所示是相机分别在位置A和位置B所拍摄的标定板图片，用来确定外部参数的符号。如图3(c)显示了在世界坐标系下标定板特征点的坐标，可以看出2个位置的标定板的对应特征点并不重合，而是有一个旋转平移关系，通过1.1.3部分计算出这个旋转平移关系参数如图3(d)所示。

图3 (a)和(b)分别是相机拍摄的位置a和位置b的标定板图片；(c)世界坐标系下标定板特征点的坐标；(d)位置a和位置b的旋转参数。

将所有特征点根据所求的参数进行重投影，得到如图4(a)和4(b)的相机和投影仪的重投影误差分布图，相机和投影仪的重投影误差分别为0.3和0.4个像素。考虑到相机1 920 ×1 200 的分辨率，该方法的精度已达到较高水平。

2.3 三维重构

为了更直观地展示所提出方法的效果，将两部分的标定参数用于远心条纹投影系统的三维重建。对如图5(a)所示具有复杂几何形状的手机金属主板进行了三维测量。对应的条纹图像和三维重建结果分别如图5(b)和5(c)所示。可见，三维重建的质量很好，证明了本文方法的可行性。

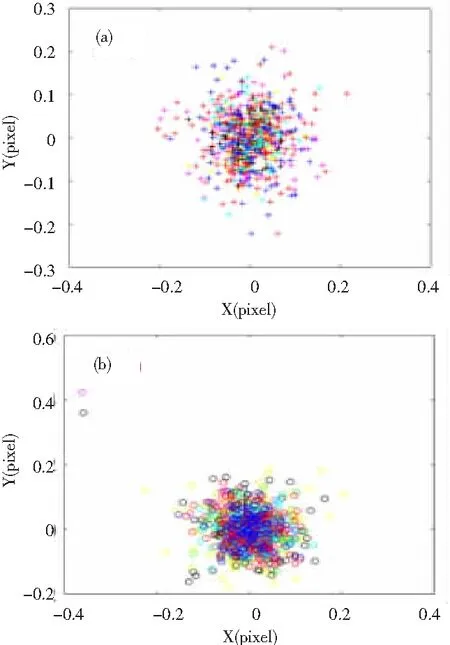
图4 相机和投影仪的重投影误差分布图

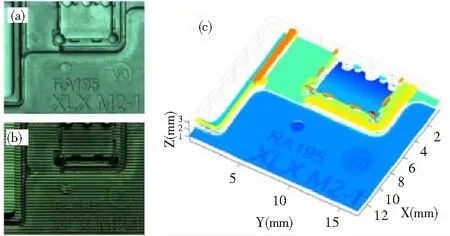
图5 (a)手机金属主板的纹理图；(b)对应的条纹图；(c)三维重建点云图

为了进一步评估所提方法的准确性，测量了一个厚度为1.06 mm的标准测量块，测量结果如图6(a)所示，并计算了标准块高度值的RMSE(均方根误差)为3.5 μm，与相机的随机噪声水平相比非常小，误差分布图如图6(b)所示。结果表明，所提出的标定方法可以实现精度良好的三维测量。

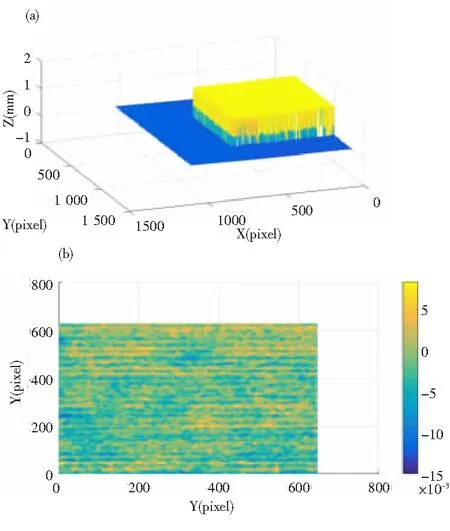
··(a)三维重建结果；(b)测量块高度误差分布图

3 结论

基于二维平面标定板的远心相机标定方法存在外部参数符号模糊问题，本文在单应性变换平面标定法的基础上，对双远心三维测量系统提出了一种便捷的标定方法，能够直接获取远心相机的外部参数。通过建立2个间隔一定高度标定板平面之间的面内旋转和平移关系，能够得到标定板平面控制点的三维坐标信息，进而完成外参封闭解的求解。该标定方法仅需要借助一个可以在参考面上任意放置的标准测量块就能完成远心三维测量系统的标定，具有高灵活性和实用性。