基于自适应radau伪谱法的机械手轨迹规划方法研究
2022-06-27陈贵亮唐润智
王 帅,杨 冬,陈贵亮,唐润智
(河北工业大学 机械工程学院,天津 300132)
0 引言
目前,随着社会发展,机械手已经得到广泛应用。但机械手在面对复杂的作业任务时,经常存在着能量消耗大、负载自重比低等问题,如何实现机械手的轨迹优化,降低机械手的关节力矩,提升机械手的负载能力是一个值得研究的问题。近年来已经有很多学者对这方面进行了研究。洪磊等人运用最小范数广义力策略优化协调操作臂载荷分配,提出了改进的三分支机器人优化关节力矩轨迹规划方法[1],但是牺牲了一部分能量消耗指标。张威等人在速度水平上对冗余机器人利用冗余特性进行了动力学优化[2],但没有在加速度水平上进行优化。金波等人提出了以降低系统能耗为目标的六足机器人力矩分配算法[3],但这种算法不一定适合于普通的机械手。邵浩然等人采用遗传算法对机械臂的各关节力矩进行了优化[4],陈珂等人采用粒子群算法对并联机器人的输出力矩进行优化[5],但是对于串联机器人并不适用。
伪谱法[6]是将连续时间最优控制问题转化为有限维的非线性规划(NLP)问题进行有效求解,首先设置一系列的配点,将控制变量和状态变量进行离散,然后在配点上进行多项式插值来逼近状态变量和控制变量进行优化,而自适应radau伪谱法[7~9]是伪谱法的一种,将整个运动过程进行分段,可以根据计算过程中的精度要求,动态调整段的个数和多项式的阶数来提高求解速率,有着收敛速度快、对初值要求不敏感等特点。江浩斌等人采用自适应radau伪谱法解决了智能汽车的轨迹规划问题[10],但是应用场景单一且并没有用于机器人。
为了证明所用方法对于机械手的普适性,且在提高机械手的负载能力方面具有优势,本文以二自由度和三自由度机械手为对象,采用自适应radau伪谱法进行轨迹优化,相比于其他算法,此方法不需要提前对机械手的轨迹进行参数化拟合。首先建立机械手的动力学模型,并以关节力矩平方和为目标函数在多约束条件下利用该种方法将最优控制问题转为线性规划问题进行求解。与五次多项式轨迹规划相比,此方法降低了机械手的关节力矩,提高机械手的负载能力。
1 动力学建模与Bolza型最优控制描述
利用拉格朗日方程可得机械臂的动力学模型为:
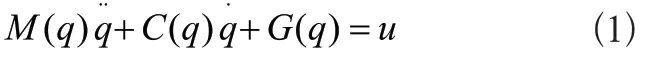
q为机械臂的关节位移,q为机械臂的关节速度,u为关节力矩,将动力学方程转化为状态方程,令x为状态向量,u为控制向量,x1=q,x2=q,x=[x1,x2],建立状态方程如下:

将动力学方程转为状态方程可得:
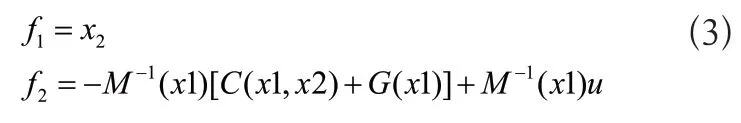
其中M为机械臂的惯性矩阵,C为离心力和科氏力矢量,G为重力矢量,t为时间。
1.1 二自由度机械手动力学模型
在机械手末端悬挂4kg重物,二自由度机械手经简化后建立如图1所示坐标系:
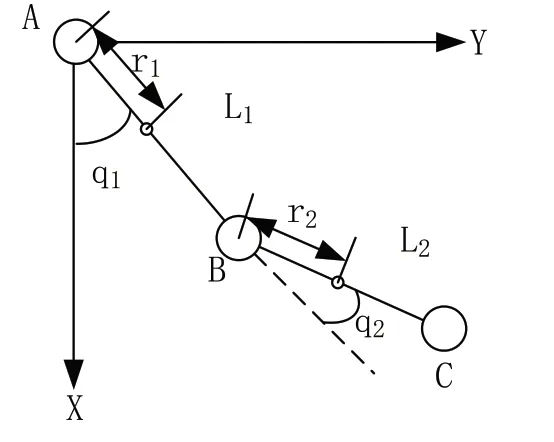
图1 二自由度机械手简化模型
将式(1)展开,利用拉格朗日方程建立机械手的动力学方程为:

其中:

式(5)中各符号代表含义及其机械手的参数如表1所示:

表1 二自由度机械手参数
1.2 三自由度机械手动力学模型
三自由度机械手经简化后建立如图3所示坐标系:

图3 三自由度机械臂简化模型
利用拉格朗日方程推导将式(1)展开可得三自由度机械手的动力学方程[11]为:

其中:

相对于二自由度机械手而言,主要是增加了旋转臂的部分,旋转臂部分的参数表如表2所示:

表2 旋转臂部分参数
1.3 Bolza型最优控制模型
Bolza型最优控制问题[12]可定义如下:

约束条件为:

式(9)中,t0表示起始时间,tf表示终止时间,约束条件中x表示状态约束,C表示路径约束,φ表示边界约束。就本研究的机械手而言,状态约束即为对机械手各关节的位置和速度的起始、终止状态约束,边界约束即限制位置、速度、关节力矩的边界条件,假设空间内无障碍物,所以无路径约束。机械手的状态约束及边界约束参数如表3所示,其中角度单位为rad,速度单位为rad/s,关节力矩单位为N·m。

表3 机械手约束
本文以机械手关节力矩的平方和最小为优化目标即:

式(10)中ui(t)表示机械臂第i个关节在t时刻的关节力矩。n表示机械臂的总关节数。
2 自适应radau伪谱法
伪谱法一般用于飞行器的轨迹优化问题,本文采用自适应radau伪谱法进行关节型机械手的轨迹优化。伪谱法是将连续的最优控制问题离散化为非线性规划问题,以拉格朗日多项式在离散点之间逼近状态变量和控制变量,求得控制变量和状态变量最优解[13];在解决复杂问题时,约束条件也在增加,最优控制问题的求解速度也在不断下降,而自适应则是在求解过程中动态调整网格区间个数和多项式阶数来实现快速收敛[14]。相比于其他方法,自适应radau伪谱法不需要提前对轨迹进行插值拟合,存在着对状态变量和控制变量求解精度高、收敛速度快的特点。
2.1 radau伪谱法
自适应radau伪谱法首先将最优控制问题的时间t∈[t0,tf]通过变换映射到伪谱法所要求的时间区间[-1,1]上,变换方程为:
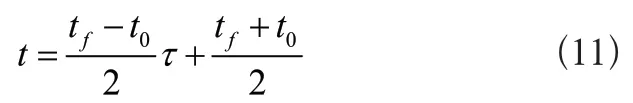
N次Legendre多项式RN(τ)的表达式为:
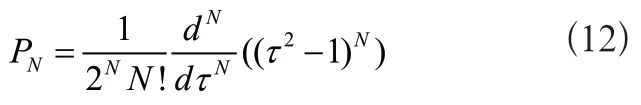
其中N个Legendre-Gauss-Radau(LGR)配点(τ1,τ2,...τN)为N 次Legendre多项式PN(τ)的零点,其中τ1=-1,τN+1=1,τN< 1。
拉格朗日基函数为:
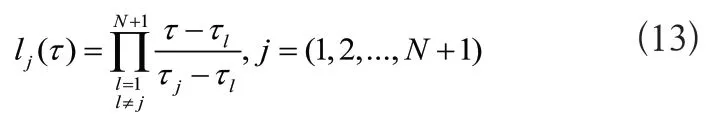
然后应用N阶拉格朗日多项式对最优控制问题的状态变量和控制变量进行类似:

其中x为状态变量,X为近似状态变量,u为控制变量,U为近似控制变量。
对式(14)求微分,可得状态变量对时间的导数为:

其中:

其中:
g(τl)=(1+τl)[PN(τl)-PN-1(τl)],ll=1,2...N+1为N次Legendre多项式PN(τ)的零点和一个终端点。
由式(16)将状态方程进行离散可得:

本研究所用的机械手是以关节力矩平方和作为目标函数,目标函数经过离散得:

2.2 自适应原则
首先考虑时间间隔t∈[t0,tf]上的Bolza最优控制问题,将整个时间间隔分成k段,每段的间隔为[t k-1,tk],Nk为每段中配点的个数,自适应算法的目标是通过确定当前网格的特定段是否已满足指定的精度公差,以计算有效的方式提高解的精度。如果未达到精度公差,则需要通过增加每段中多项式的阶数或进一步划分段来修改配点的数量和分布[15]。
若通过多项式阶数来更新,则Nk-和Nk+为更新前后每个时间段内的配点数,其与误差容忍度εd和在每一时间段内通过设定离散状态方程和路径约束的最大误差值e(k)max的关系表达式为:
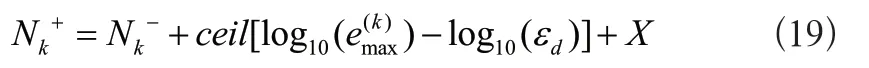
其中X为任意整数常量,控制每一段内配点数的增长数,而ceil是舍入到下一个较大整数的运算符。
若通过进一步划分段来修改配点的数量和分布则子区间段的个数可表示为:
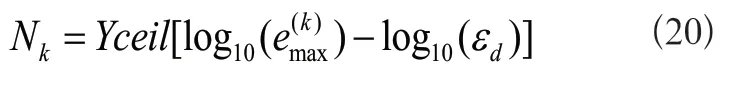
其中Y为任意的整数常数,来控制子区间段的个数。而ceil是将参数舍入为+∞的运算符。
3 系统仿真
3.1 仿真设定
针对机械手的负载能力提升问题,在轨迹规划时以降低机械手的关节力矩为目标,以二自由度机械手和三自由度机械手模型为例,以关节位置、速度作为状态变量,关节力矩作为控制变量,采用自适应radau伪谱法对机械手进行轨迹优化,首先设置机械手的状态约束和边界约束,具体参数如表3所示,然后利用已建立的机械手动力学模型进行关节力矩的求解,代入以关节力矩平方和作为优化目标函数,利用MATLAB外接的gpops-Ⅱ[16]软件进行求解。建立机械手的五次多项式轨迹规划,并与自适应radau伪谱法进行对比,验证优化方法的有效性,仿真时长设置为1s。
3.2 仿真结果
图4(a)、图4(b)和图4(c)分别为二自由度机械手经过五次多项式规划的的关节位置、速度和力矩图像,图4(d)、图4(e)和图4(f)分别为三自由度机械手经过五次多项式规划的关节位置、速度和力矩图像。由图像可以看出,各关节在达到设定的位置时,关节力矩呈现升高-降低-再升高的趋势,时间在0.2s时关节力矩达到峰值。

图4 机械手五次多项式轨迹规划
图5(a)、图5(b)为二自由度机械手经过伪谱法和五次多项式关节力矩对比。图5(c)、图5(d)为优化之后机械手的关节位置、速度图像。由图可知,在整个运动过程中,经过优化之后大臂力矩相对于优化前呈整体降低的趋势,小臂力矩在初始时有一个较高值,但随着机械臂的运动,不断低于优化前,且总体呈平稳趋势。图6(a)、图6(b)和图6(c)分别为三自由度机械手经过伪谱法和五次多项式关节力矩对比,图6(d)、图6(e)为优化之后机械手的关节位置、速度图像。由图像可以看出,优化后旋转臂关节力矩相比于优化前呈平稳下降趋势,大臂关节力矩在0.3s左右达到峰值,且比优化前幅值下降了约为10N·m,之后平稳下降。小臂的关节位置、速度相比于其他两个关节有一个较大的浮动,关节力矩优化后在初始时刻即为峰值,且为优化前的四倍,但随着时间进行,逐渐降低,从全局来看,总体还是呈下降趋势。

图5 二自由度机械手伪谱法与五次多项式关节力矩对比

图6 三自由度机械手伪谱法与五次多项关节力矩对比
对于机械手模型,在整个的仿真过程中,小臂关节在初始时刻要大于优化前的关节力矩,但随着仿真的运行,关节力矩逐渐低于优化前,机械手其余各关节力矩相比于优化前呈总体降低的趋势,从而提高了机械手的负载能力,也间接地降低了能耗,证明了所采用方法的合理性、有效性。
4 实验
实验器材为自主研制的HEBUT-Ⅱ型三自由度机械手,旋转臂的传动比为120,大臂的传动比为100,小臂的传动比为80,各臂质量、长度等参数如表1、表2所示,电机均为安川电机,额定扭矩为1.27N·m。型号为SGM7J-04A,控制系统由凌华PCI-8258DSP型8轴高级运动控制卡和工控机组成,采用Labview作为上位机开发软件进行实验。
由于位置控制时受位置精度的影响,电机的扭矩输出无规律性,与仿真相差较大,故实验采用力矩控制模式,通过Labview编程分别将经过自适应radau伪谱法和五次多项式规划的关节力矩经过换算转为输入电压,输入到伺服驱动器以驱动电机进行关节的转动,将伺服驱动器的模拟量输出CN5端口与数据采集卡的模拟量输入端口相连,读取反馈回来的电压值,然后将电压值经过换算转为力矩值,作为我们的实验力矩输出值。实验场景如图7所示。

图7 实验场景
实验得到的数据如图8所示,图8(a)、图8(b)为二自由度机械手实验后的关节力矩对比图像,图8(c)、图8(d)和图8(e)分别为三自由度机械手实验后的关节力矩对比图像。在力矩控制模式下,机械手基本上能达到各关节位置,对于二自由度机械手,优化后的关节力矩在初始时刻有所降低,与仿真时相差不大,大臂关节力矩在最后时刻趋于同一值,总体呈平稳下降趋势,产生的关节力矩较小。对于三自由度机械手,在运行过程中在某一时刻有尖点的存在,是由于伺服系统反应速度(高)与机械传递或者反应时间(较长)不相匹配而引起的,旋转臂关节一直呈平稳下降趋势,大臂关节的峰值依然小于优化前,但峰值出现在0.4s左右,相比于仿真峰值出现时间延后了0.2s,小臂关节的力矩呈现降低-升高-再降低-再升高的趋势,且在0.5s时刻关节力矩大于优化前,这可能是由于机械手各关节本身存在的摩擦,机械臂为非均质杆导致动力学模型不准确的原因,但从总体来看,实验所得关节力矩的图像与仿真基本上趋势相同,优化之后的关节力矩相比优化前峰值明显降低,也就是提高了负载能力。

图8 关节力矩对比实验
5 结语
本文以降低机械手的关节力矩,提升负载能力为目标,采用自适应radau伪谱法对机械手进行轨迹优化。根据二自由度和三自由度的机械手动力学模型,以位置、速度作为状态变量,力矩作为控制变量并考虑运动过程中的状态约束、边界约束,以关节力矩平方和作为优化目标函数,将运动过程中的连续最优控制问题转化为非线性规划问题。此种算法在求解过程中可动态调整运动过程分段个数和多项式阶数来提高求解速率。由仿真可得优化后的机械手在达到关节位置后,其关节力矩相比于优化前都有了很大程度的降低,即在不更换电机及驱动器的前提下,给它同等大小的力矩可以提升更重的物体,也就是提高了机械手的负载能力。也间接降低了机械手的能耗,并通过实验验证了此种方法的合理性,有效性。本文并没有再对更多自由度的机械手进行研究,也为后续其他学者在用此方法进行更多自由度的机械手在进行搬运任务时的轨迹优化提供了研究思路。
