基于模糊PID的挂面烘房温度控制

王泽教，王恒升,2*，江亮亮，赵志刚

（1.中南大学机电工程学院，长沙 410083；2.中南大学高性能复杂制造国家重点实验室，长沙 410083）

0 引言

挂面在我们生活中是一种常见的食物。在挂面的加工制作过程中，有一道关键的工艺就是对挂面进行烘干处理。该工艺的难点在于控制烘房的温度[1]。目前大多数工厂对温度的控制还停留在手动控制阶段，这种控制方式精度低、温度波动较大，还会造成能源的浪费[2]。为此急需建立烘房的温度模型，设计温度控制器，实现温度的自动控制，提高控制精度。

挂面烘房温度系统是一个非常复杂的系统，主要受该烘房的湿度、相邻烘房的温湿度、外界环境的温度以及供热介质油温度的影响。为了提高烘房温度的控制精度，国内外有很多学者对烘房、温室等小气候环境温度模型及控制开展过相关研究。高亚军[3]曾对挂面烘房的温湿度平衡做过研究，通过对烘房内部的耗热量及供热量进行分析，建立热平衡方程，为烘房的供热量提供了参考价值。张芬等[4]在烟叶烘房的温度控制系统中，设计模糊自整定控制器，仿真结果表明该控制器能有效的提高烘房温度的控制精度，具有更好的稳定性和鲁棒性。徐玲等[5]在黄酒发酵的温度控制中，通过辨识方法得到温度数学模型，并设计了基于Smith预估的PID控制器，仿真结果表明控制器有效的降低了延迟对系统的影响，明显缩短了调节时间。丰会萍等[6]基于RBF神经网络设计了PID控制器对温度进行控制，通过实验表明该控制器减小了超调量，温度控制精度在1.5%以内。He Haiyan等[7]在玫瑰温室的温度控制中，基于BP神经网络设计了模糊控制器，使系统获得了更好的增益性能。Hampus Carlborg等[8]在工业炉的温度控制中，采用黑箱建模得到温度模型，并使用模型预测控制(MPC)对温度进行预测，通过仿真验证了该控制器能减少系统开关次数，提高了度控制精度。N.N.Mohammad等[9]在蒸馏水温的控制研究中，将MPC控制算法与PID控制算法进行对比，实验表明MPC算法能更好的抵抗外界的干扰，提高系统的稳定性。

本文针对挂面烘房的多工况、环境复杂、参数时变、难以建立精准数学模型等问题，初步建立温度的数学模型，并设计模糊PID控制器，以提高温度控制精度，提高系统的抗干扰能力。

1 烘房温度系统建模

1.1 烘房概况介绍

本工作以湖南某挂面加工厂烘烤线温度系统为研究对象，烘烤线的平面分布情况如图1所示，总体尺寸为：长36.8m，宽14.7m，高3.7m。整条烘烤线分为4个连通的温区（或烘房区）。烘房通过锅炉加热介质油循环供热，烘房底部设有通风口，通过抽湿机排出水蒸气。4个烘房中2号烘房的温湿度控制最为重要，生产时要求温度控制在45℃±1℃，相对湿度控制在78%±2%。本工作主要以2号烘房为例，建立温度模型并设计控制器，提高该烘房温度系统的控制精度。

图1 烘烤线分布图

1.2 温度模型的建立

温度系统建模主要有数据建模[10，11]和机理建模[12～14]两种方法。烘房的温度系统环境复杂，受多因素影响，本文对各因素进行分析，建立其机理模型。

根据热力学第一定律可知，系统内能的增量等于外界相互传递的热量与外界做功的总和。对2号烘房总热量变化分析，主要由两部分引起的：一部分是2号烘房与相邻烘房、锅炉介质油以及外界环境之间的热交换；另一部分是2号烘房内部面条水分蒸发消耗的热量。其热量平衡方程如式(1)所示。

式(1)中Q表示热量，单位为w，下标表示两烘房热量的传递，如Q21表示1烘房与2烘房的热交换，Qn表示面条消耗的热量，ΔQ表示2烘房的热增量。

1.2.1 烘房内的温度变化

烘房内热量的变化会引起温度的变化，其对应关系如式(2)所示：

式(2)中ρa表示空气密度，kg/m3；Ca为空气的比热容，J/(kg·℃)；Va为烘干房的体积，m3；T2为2号烘房的温度，℃；t为时间，s。

1.2.2 烘房和外界环境之间的热交换

该部分热交换主要是通过烘房的房顶、地面、墙体的热交换，以热传导方式进行交换。

式(3)中A20表示房顶和地面的面积，m2；k20表示房顶和地面的换热系数，w/(m2·℃)；T0表示外界环境的温度，℃。

1.2.3 相邻烘房之间的热交换

该部分热交换主要是2号烘房和1、3烘房的热交换，包括两部分：通过墙面的热传导和经过面条通道的空气对流换热。其中主要是热传导引起的，面条通道非常小，行走速度低，引起的对流换热影响相对较小。

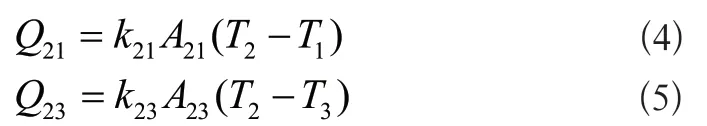
式(4)中K21表示1、2烘房之间墙体的导热系数，w/(m2·℃)；A21表示1、2烘房之间墙体的面积，m2；T1表示1号烘房的温度，℃；K23表示2、3烘房之间墙体的导热系数，w/(m2·℃)；A23表示2、3烘房之间墙体的面积，m2；T3表示3号烘房的温度，℃。

1.2.4 介质油供热

烘房的热量主要是通过介质油提供，通过锅炉加热介质油，再利用管道循环输送介质油到各烘房，利用烘房里分布的散热片传递热量。

式(6)中A24表示散热片的表面积，m2；k24表示散热片的导热系数，w/(m2·℃)；T4表示介质油的温度，℃。

1.2.5 面条蒸发耗热

面条烘干主要是由于面条内部的水分蒸发，在蒸发过程中会消耗大量的热量，这部分热量称为汽化潜热，属于食品干燥中重要的基本参数[15]。烘房里水分汽化消耗的总热量可以按照下式计算：

式(7)中mv表示烘房内单位时间产生的水蒸气质量，kg/s；r表示蒸发潜热，J/kg。

蒸发潜热可以根据实验直接测量，或者根据气压计算。不同的温度对应的潜热值不同。本文通过温度与潜热的相关数据，利用一次函数拟合潜热与温度的表达式：

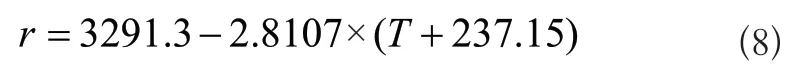
式(8)中T表示对应的温度，℃。

由于蒸发的水蒸气产量无法直接测量，可以根据室内的相对湿度计算出水蒸气产量。根据室内水蒸气含量平衡方程可知，水蒸气的变化量等于水蒸气的产量与排放量之和，则可以建立湿度模型如下：

式(9)中V2表示2号烘房的体积，m3；F20表示2号烘房通风口的空气流速，m/s；A20表示通风口的面积，m2；F21表示1、2烘房通道的空气流速，m/s；F23表示2、3烘房通道的空气流速，m/s；χ1表示1烘房的水蒸气密度，kg/m3；χ2表示2烘房的水蒸气密度kg/m3；χ3表示3烘房的水蒸气密度，kg/m3。

由式(7)～式(9)可知，水分汽化消耗的总热量与温度和水蒸气密度的乘积有关，存在一定的耦合关系，对后续的参数辨识增加难度。采用式(10)对其进行转换，使系统的模型得以简化。

式(10)中R表示单位体积水蒸气所消耗的能量，J/m3。

将式(2)～式(10)代入到式(1)可以得到烘房温度系统的动态模型。

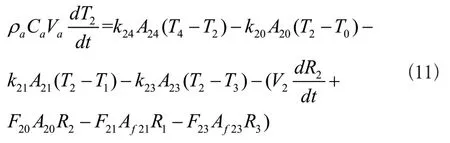
通过对烘房温度系统进行分析，建立机理模型，从模型中可知，该系统存在多变量、强干扰、参数时变等特点。

2 模糊PID控制器的设计

烘房的温度系统较为复杂，特别是存在多种工况，且环境因素干扰较大，导致系统的参数存在一定的时变性，常规控制方法难以达到控制目标。图2是一种模糊PID控制框图，图中r表示目标值，y0表示传感器采集的实际值，u表示控制量，y表示模型输出值，N表示系统的干扰量。利用模糊控制器实时修改PID控制器的参数，实现PID参数自动调整，适应不同工况，提高控制系统的精度以及抗干扰能力。

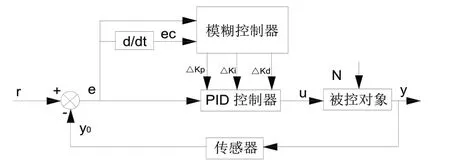
图2 模糊PID控制器

2.1 模糊控制器的设计

模糊控制器的基本原理图如图3所示，模糊控制器主要可以分为四个部分：模糊化、规则库、模糊推理和解模糊。

图3 模糊控制器原理图

2.1.1 输入输出的确定

模糊控制器采用两输入三输出结构，如图4所示。以信号的偏差e以及偏差变化率ec为输入量，以3个PID参数的修正值ΔKp，ΔKi，ΔKd为输出量。

图4 模糊控制器

设计模糊控制器时，为了提高控制精度，通常将输入输出进行量化处理。根据工厂采集的实际数据分析可知，在开始工作时，温度误差可以达到15℃，偏差变化率为1℃，则e的基本论域可以设置为[-15，15]，ec基本论域为[-1，1]。控制器中输入量的模糊论域都设置成[-50，50]。通过计算可以得到输入的量化因子ke1=3.3，kec1=50。

模糊控制器的输出论域中，Δkp和Δkd输出参数的模糊论域设置为[-50，50]，Δki对系统的误差积分影响较大，模糊论域设置成[-30，30]。通过对系统进行PID控制仿真测试，可以确定Δkp的基本论域为[-25，25]，Δki的基本论域为[-2.5，2.5]，Δkd的基本论域为[-5，5]。则输出的量化因子kup=0.5，kui=0.05，kud=0.1。

为了使变量描述更加准确，通常将模糊论域划分为不同的等级，每个等级选择对应的隶属度函数，文中将模糊论域划分为7个等级，都选择三角形隶属度函数，每个隶属度函数的区间如表1所示。

表1 模糊论域划分区间

2.1.2 模糊推理

模糊推理是模糊控制器的核心部分，利用规则库的相关信息，结合操作人员的实际工作经验，对系统的输入输出进行逻辑推理。本文采用Mamdani法进行模糊逻辑推理。其基本表达方式如下：

If e and ec then △Kp and △Ki and △Kd

在进行模糊推理时，需要根据不同的e和ec值确定PID的参数，可以根据以下的方法进行推理：

1）e和ec都比较大，方向相同：表明偏差值会越来越大，应该取较大的PID修正值，使系统更快的到达目标值；

2）e和ec都比较大，方向相反：表明偏差值会减小，适当减小PID修正值，避免引起系统超调；

3）e和ec一大一小：通常可以将PID参数设定成中等大小值；

4）e和ec都比较小：表明系统基本趋近于稳定值，PID修正值应设置在0附近，只需进行微调。

参照目前在7等级隶属度函数中常用的49条规则，结合上述的PID参数推理方法，对输入输出量进行推理，得到模糊控制器的推理规则如表2所示。

表2 模糊推理规则表

2.2 PID控制器设计

PID控制器结构简单，参数设计方便，使用范围广，但是传统PID控制的参数固定，对于参数具有时变性、强干扰的系统，传统PID控制器难以达到理想的控制效果。使用参数自整定的PID控制器，能根据系统的实际情况实时修正PID的参数值，获取更好的控制效果。PID的参数计算方法如式(12)所示：

式(12)中kp，ki，kd为整定后的PID参数。Δkp，Δki，Δkd为模糊控制器的三个输出参数；kp0，ki0，kd为PID控制器的三个初始参数。

对于PID初始参数的设定，可以采用在线调整的方式，但是在线调整参数过程复杂，需要消耗大量的时间进行测试。在确定了温度系统模型之后，可以直接根据模型离线计算出初始参数。本文根据所建立的温度系统模型，在MATLAB中通过Simulink模块进行离线仿真调试PID参数，利用PID模块自动调节系统的PID参数，得到初始参数：kp0=50，ki0=0.05，kd0=0。

3 仿真实验分析

采集工厂正常生产时的温湿度数据，利用最小二乘法[16]对式(11)的参数进行辨识，得到系统的模型如下：

式(11)中D2表示R2的微分项。

以MATLAB里的Simulink工具箱为实验平台，搭建温度系统控制模型。工厂实际工作时，2烘房的温度设定值为45℃，仿真过程中模型的输入值设为45℃的常量。仿真时，将工厂采集的干扰信号作为图2中的干扰量输入到模型中，使模型更接近真实情况。在仿真过程中，分别对模型采用传统PID控制和模糊PID控制，两种控制方法的结果如图5所示。

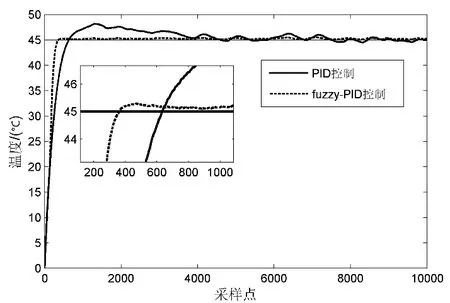
图5 温度系统仿真曲线

通过对图5两种控制器的仿真曲线可知：

1）两种控制器中PID的初始参数相同，所以开始阶段曲线变化一致，后期通过模糊控制器对PID参数的修正，模糊PID控制系统的响应速度明显加快，性能优于传统PID控制器；

2）通过对仿真数据计算分析，模糊PID的超调量为1.15%，调节时间为398s，传统PID的超调量为7.09%，调节时间为5554s。模糊PID控制系统具有更好的动态性能；

3）仿真过程中，系统引入了部分干扰信号，从仿真曲线可以看到，模糊PID控制器始终处于设定值附近，基本没有波动。传统PID控制器在干扰情况下，温度波动较大，难以达到目标控制效果。表明模糊PID控制器能更好的抵抗外界的干扰，提高系统的稳定性。

4 结语

针对烘房温度系统工况复杂，环境干扰量大，温度控制精度低、波动大等问题，建立了温度机理模型，并设计了模糊PID控制器。文中通过建立的模型进行离线仿真，确定模糊控制器的参数以及PID控制器的初始参数。通过模糊控制器实时调整PID控制器的参数，实现了PID参数自动整定功能。通过将工厂正常生产的实际数据输入到仿真模型中，验证了该控制系统具有更小的超调量，更强的抗干扰能力，适用于不同的工况，能有效的减小温度的波动，对实际的温度控制有一定的参考价值。