基于复杂网络的波罗的海原油运价指数波动规律研究
2022-06-26林舒暖张婕姝
林舒暖 张婕姝


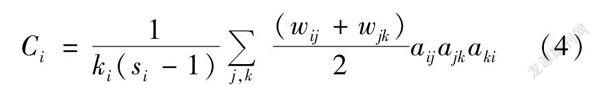


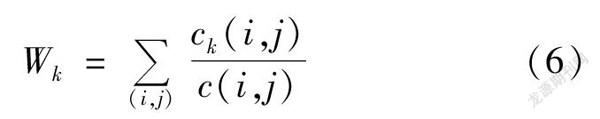








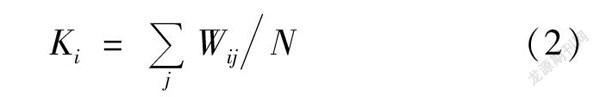


摘要:波罗的海原油运价指数(Baltic dirty tanker index, BDTI)是油船运输企业把握油运市场景气程度的“风向标”,为揭示其波动规律,采用复杂网络理论对其进行研究。通过分析加权度、中心性、n派系、k核等网络拓扑结构指标,得到BDTI的波动特征:BDTI复杂网络呈无标度特性,处于网络核心位置的8种主导模态构成一个单向闭环进行8个滑动周期传导,对BDTI波动信息传导起到重要作用。n派系和k核分析结果表明,BDTI复杂网络具有周期波动性、类群集聚性、渐进传导性。BDTI正常上升主要发生在9月、10月、11月,正常下降主要发生在2月、4月、5月,且不存在明显的自传导特征。
关键词: 水路运输; 复杂网络; 波罗的海原油运价指数(BDTI); BDTI复杂网络; 波动特征
中图分类号: F550.5文献标志码: A
Study on fluctuation law of Baltic dirty tanker
index based on complex network
Abstract: The Baltic dirty tanker index (BDTI) is the “weathervane” for tanker transportation enterprises to grasp the oil transportation market boom degree. In order to reveal its fluctuation law, it is studied by the complex network theory. By analyzing the network topology indices such as the weighting degree, centrality, ncliques and kcore, the fluctuation characteristics of BDTI are obtained as follows: the BDTI complex network is scale free, and the 8 dominant modes at the core of the network form a oneway closed loop for 8 sliding cycle conduction, which plays an important role in the BDTI fluctuation information transmission. The analysis results on ncliques and kcore show that, the BDTI complex network is of periodic fluctuation, class clustering and progressive conductivity. The normal increase of BDTI mainly occurs in September, October and November, while the normal decrease mainly occurs in February, April and May, and there is no obvious selfconduction characteristic.
Key words: waterway transportation; complex network; Baltic dirty tanker index (BDTI); BDTI complex network; fluctuation characteristic
引言
波羅的海原油运价指数(Baltic dirty tanker index, BDTI)由波罗的海航运交易所发布,具有公认的权威性,是衡量油船运输市场景气程度的“晴雨表”,分析研究历年来BDTI的波动幅度及运价走势,对油船运输企业制定相关经营策略和规避相关海运风险具有十分重要的意义。目前已有众多学者从不同的视角对BDTI波动规律进行了大量研究。LI等[1]利用BP模型预测了BDTI走势,分析BDTI短期和中长期发展动态。FAN等[2]采用小波分析指出,BDTI波动具有非线性和非平稳性。文献[35]分别采用灰色关联理论、经验模式分解、组合预测模型3种不同的方法对油船运价指数波动规律进行了分析,表明油船运价指数波动与其他时间序列变量存在强相关性。文献[67]采用计量经济学方法有效评估了BDTI的风险价值,为测度BDTI的投资风险提供了新思路。匡海波等[8]基于BDTI波动不确定性风险的分析表明,BDTI的波动在短期内符合几何布朗运动方程。文献[910]均对BDTI进行了多重分形分析,结果发现该时间序列均出现了明显的多重分形特征。冯文文等[11]对BDTI波动机理进行的分析表明,BDTI具有显著的均值回归特性。
上述学者采用了非网络化的理论方法对BDTI波动规律进行探究,而在运用复杂网络方法上,ADLAND等[12]利用非参数马尔科夫链研究了即期油船运价的波动性,认为非线性随机模型最能描述运价的波动特性。安海岗等[13]较早地将复杂网络方法应用到时间序列分析中,为油船运价时间序列分析拓展了新思路。周洁[14]采用网络演化动力学分析指出,代表原油价格短期波动趋势的高频油价、原油库存和美元指数三者联动阈值网络更加接近“小世界网络”。在集装箱运价指数研究中,汤霞等[15]运用系统动力学方法构建中国出口集装箱运价指数(China containerized freight index, CCFI)波动复杂网络模型,表明集装箱运价波动存在周期性和渐进性。
现阶段对BDTI研究甚多,但是运用复杂网络理论对其波动规律进行研究的成果较少。复杂网络理论是系统科学和复杂科学研究的重要理论之一,主要通过分析系统网络的拓扑结构性质,从中探究不同系统主体之间的关联程度。目前已广泛应用于社会关系、能源、金融、国际贸易等领域,类似于金融市场的股票指数波动传导机制研究,复杂网络理论应用于原油运价指数具有一定的适用性,但这方面的研究有待完善。
本文基于复杂网络理论对BDTI波动特征进行分析,通过构建BDTI波动有向加权网络模型,计算其加权度、加权集聚系数、中心性、n派系(ncliques)、k核(kcore)等网络拓扑结构指标,分析BDTI波动的内在规律,帮助油船运输企业及时掌握油运市场行情动态,在短期内准确把握运价走势,提前制定相关经营策略以应对市场不确定性。
1BDTI复杂网络模型构建
首先将BDTI数据按照“3σ原则”进行粗粒化处理,将其转化为符号序列(波动模态),构建一个以波动模态为节点,模态之间的转换关系为边、转换次数为权重的有向加权网络模型,对BDTI波动规律进行研究。
1.1BDTI数据粗粒化处理
选取2000年1月—2020年12月(共21年)的BDTI为原始数据,数据来源于Clarkson Research。为了解探究BDTI波动特性,将相邻两个月的BDTI的差值定义为运价波动幅度,即ΔEBDTI(t)=EBDTI(t)-EBDTI(t-1),EBDTI(t)为时间t的BDTI值,绘制BDTI波动幅度趋势图,见图1。
在充分考虑“3σ原则”基础上,对BDTI数据进行粗粒化处理。将运价波动状态定义为Fi, Fi∈(U,u,o,d,D),其中U代表异常上升,u代表正常上升,o代表不变动,d代表正常下降,D代表异常下降。波动状态判断如式(1)所示,其中μ和σ分别为ΔEBDTI的均值和标准差。取BDTI连续3个月的符号序列作为一个波动模态,利用数据滑动窗,以3个月为滑动窗口,以1个月为步长,对其进行粗粒化处理,具体见表1。(1)
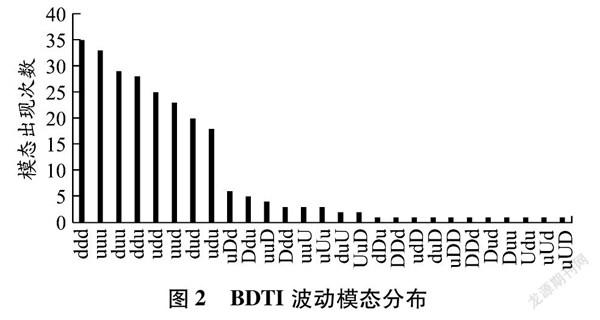
对BDTI数据进行粗粒化处理后,应该有125(53)种波动模态,但从图2发现,只出现了27种波动模态。从图2波动模态分布可知,只有少数模态在波动传导中出现频率较高,多数模态出现频率低,其中ddd、uuu、duu、ddu、udd、uud、dud、udu这8种模态的出现频率较高,即连续3个月BDTI表现出正常上升、正常下降、正常升降的状态较频繁,并且这8种模态中均不包含“D”或“U”等异常状态,说明2000—2020年BDTI连续3个月处于正常升降的波动状态。27种模态中均不包含“o” 状态,即不存在BDTI不变动现象,说明BDTI连续3个月的波动变化是动态发展的。
1.2BDTI波动有向加权网络模型构建
构建以波动模态为节点,模态之间的转换关系为边、转换次数为权重的网络模型。如图3所示,其中边的粗细表示模态之间转换次数的权重大小,模态之间转换频率越高,有向加权边的权重就越大,边就越粗。经统计,该有向加权网络中共有27个节点和249条边。
由表2可知:在模态转换过程中,从ddu到duu的转换出现了20次,其对应的边的权重最大;有24对模态的转换次数为1,它们对应的边的权重最小,且都包含了U和D。由图3可知,转换较频繁的8种模态形成了一个单向闭环,即duu→uuu→uud→udu→dud→udd→ddd→ddu→duu,由此可知该8种模态对BDTI的波动传导起到核心作用,且都属于正常升降,无异常上升、异常下降以及不变动,反映了BDTI的波动传导存在一定的规律性。如连续3个月波动呈现duu时,很大程度上该模态会朝着uuu方向变动,即第4个月出现“正常上升”的概率大。如此反复循环,可为油船运輸企业预测油运市场运价波动提供一定的指导。
2BDTI复杂网络结构分析
2.1加权度
在构建的BDTI复杂网络中,模态的加权度越大,该模态就越重要,出现频率就越高,向其他邻近模态转换的次数就越多。模态i的加权度(2)式中:N表示所有模态加权度的累计值;Wij表示从模态i转换到模态j所能经过的最少模态数。平均加权度(3)根据式(2)计算各模态的加权度,结果见表3。从表3可知,前8个模态duu、ddu、udd、uud、dud、udu、ddd、uuu的加权度均超过30,累计加权度分布达到81.77%,与上述网络图中形成的单向闭环相呼应。
根据式(3)计算平均加权度,可得整个BDTI复杂网络的平均加权度为7.93,表明网络中平均每个模态与其他8个模态相连。对模态的加权度Ki和排名次序li进行双对数处理(见图4),得到回归方程y=-1.45x+5.41(这里x=ln Ki,y=ln li),可决系数为0.855,说明BDTI波动模态呈幂律分布,体现了网络的无标度特征,即只有少数模态与其他模态之间存在多边相连,比如duu、ddu、udd、uud等。这些模态在网络中具有强控制能力,向邻近模态转换的路径多,这意味着一旦BDTI连续3个月出现这些模态,油船运输企业需提前拟定多种运价走势方案,以降低油运市场风险损失。
2.2加权集聚系数
模态的集聚系数用来反映BDTI复杂网络中各个模态与邻近模态之间进行信息传导的聚集程度。模态集聚系数越大,在网络中就越重要。模态i的加权集聚系数(4)式中:ki表示模态i的强度;si表示模态i的度值;wij表示从模态i到模态j的连边的权重;wjk表示从模态j到模态k的连边的权重;aijajkaki表示 i、j、k能否构成三角形,其中aij表示邻接矩阵元素,若模态i与模态j之间有边直接相连,则aij=1,否则aij=0。
由表4可知,BDTI复杂网络中的前10个模态的加权集聚系数均不为0,且与每个模态构成三角形的其他两个模态均位于单向闭环内,说明加权集聚系数越大的模态,向单向闭环中的8种主导模态传导信息的概率就越大,越有可能触发闭环,使其以8个滑动周期循环转换。油船运输企业需密切关注加权集聚系数大的模态。
2.3接近中心性和介数中心性
接近中心性用于反映模态在网络中居于中心的程度,介数中心性用来分析模态在网络中的中介作用。
模态i的接近中心性(5)式中: dij表示从模态i到模态j的最短路径;M表示节点总数。
模态k的介数中心性(6)式中:c(i,j)为从模态i到模态j的最短路径的总数;ck(i,j)为从模态i到模态j的最短路径中经过中间模态k的路径数。
根据式(5)和(6)可计算得到27种模态的接近中心性和介数中心性,经分析发现,两者之间并不存在强相关性。如图5所示,接近中心性最高的模态为ddu,其中前12个接近中心性较高的模态(duu、ddu、udd、uud、dud、udu、ddd、uuu、uDd、Ddu、uuD、Ddd)的累计贡献率达52.55%,说明这12个模态中心性突出。而在网络的波动传导过程中扮演中介作用的主要是duu、ddu、dud、uDd、Ddu等模态。接近中心性较高的模态向下一模态转换或者由上一模态转换而来所经过的路径较短,直接连通性较强,以duu→uud转换为例,其转换只需要经过一步,而不需要经过以uuu为中介的duu→uuu→uud的两步转换。如果出现接近中心性较高的模态,那么它下个月向与它紧密相连的模态进行信息传导的速度将会很快。对于油船运输企业而言,要及时做好运价不常态化波动的准备,妥善布局油船运力和做好风险管控。
2.4n派系
为探究BDTI模态聚类程度,采用n派系方法对BDTI复杂网络进行模态子群聚类。令n=2,当模态规模大于或等于6时,BDTI复杂网络被聚类成5个子群,如表5所示。子群内任意2种模态之间的转换均不超过2步,直接转换的概率高。将5大子群细分为3类:1号子群内u符号出现次数较多,属于Ⅰ类正常上升子群;2号、4号子群内d符号出现次数较多,属于Ⅱ类正常下降子群;3号与5号子群内u和d符号出现次数相当,属于Ⅲ类正常升降子群。当某种模态出现时,由它向同类子群模态转换的概率较高,1号、2号、3号子群模态向该类子群内任意模态转换的概率为16.7%,4号、5号的转换概率则为20%。以Ⅰ类子群为例,当uuu模态出现时,它有16.7%的概率向uuu或uud或uuU转换。依照每类子群的模态传导规律,可为油船运输企业在发现BDTI的波动模态属于某一子群时,提供至少2到3个月的运价预测。
2.5k核分析
为进一步探究BDTI复杂网络中模态间的传导特征,引入k核机制。将度小于k的节点以及相应的边删除,余下子图的节点作为k核,k核节点具有较强的连通性和传导性。对BDTI复杂网络的节点进行3核解析后结果见图6。
由图6可知,将BDTI复杂网络进行3核解析后,只剩下6种模态,解析后的网络形成了一个权重较大的6种模态链路,即duu→uud→udu→dud→udd→ddu→duu,说明当BDTI波动处于该链路上的某一模态时,有很大概率该模态会沿着此链路向下一模态转换。若出现uud模态,则经历6个滑动周期后相应会出现uud→udu→dud→udd→ddu→duu→uud的模态传导。从模态传导过程可知,BDTI波动具有渐进传导性和周期波动性,且持续正常升降状态是比较常见的,而异常升降或者不变动状态出现的概率较低。
对BDTI复杂网络进行3核解析后,将权重较大的6种模态的演变时间和转换模态进行统计,见表6。由表6可知,2000—2020年BDTI波动期间,k核闭环内发生模态转换次数最多的是从udd至ddu,累计达到25次,说明在BDTI复杂网络中,udd与ddu两种模态之间的转换较为频繁。duu→uud3核解析
模態转换发生了22次,其中在2月发生正常下降次数最多;uud→udu模态转换发生了14次,正常上升主要发生在10月;udu→dud模态转换发生了13次,在4月表现出正常下降变化最为频繁;dud→udd模态转换时间主要集中于2月和5月;udd→ddu模态转换多发生在9月和10月,其中9月发生的频次最高;ddu→duu模态转换出现了21次,其正常上升主要发生在10月和11月。3核解析后,BDTI均未出现连续3个月正常上升(uuu)或者连续3个月正常下降(ddd)的模态,说明BDTI不存在明显的自传导特征,即uuu→uuu或者ddd→ddd。
3核解析后发现,BDTI正常上升主要发生在9月、10月、11月,正常下降主要发生在2月、4月、5月。因此,对于油船运输企业而言,可提前签订新船订单或者购买二手船、适当开辟新的航线,以及释放更多的浮仓储油运力,以便在BDTI处于正常上升的9月、10月、11月投入运营赚取更多利润;同时在BDTI正常下降的2月、4月、5月可适当采取拆解报废部分油船、利用淡季时间安排油船维修保养、改变航线布局等策略,缓解油船运力过剩,减少利润亏损。
3结论
波罗的海原油运价指数(BDTI)是原油运输市场的“晴雨表”,能衡量原油运输市场的景气程度,因此分析BDTI的波动规律,有助于油船运输企业对市场行情进行预判和风险管控。本文通过复杂网络理论对BDTI复杂网络进行拓扑结构探究,揭示BDTI运价波动的动态特征和内在规律。结果显示,BDTI波动有向加权网络模型主要由duu→uuu→uud→udu→dud→udd→ddd→ddu→duu形成的单向闭环对BDTI波动进行8个滑动周期的信息传导,这说明BDTI存在一定的周期波动性,该闭环中的8种模态控制着BDTI波动信息传导,处于网络的核心位置。通过子群聚类,将模态划分成3大类,表明BDTI波动具有类群集聚性。3核解析下,剩余的6种主导模态duu→uud→udu→dud→udd→ddu→duu形成一条链路,表明BDTI复杂网络具有渐进传导性。BDTI正常下降主要发生在2月、4月、5月,BDTI正常上升主要发生在9月、10月、11月,且不存在明显的自传导特征。
受新冠肺炎疫情以及石油价格不确定等因素影响,2020年BDTI波动幅度颠覆历年来的变化水平,这给油船运输企业运力投放及经营管理带来了巨大的风险。因此,如何在不确定市场中把握运价波动趋势,成为油船运输企业重点关注的目标。根据本文研究结果,建议油船运输企业密切关注由8种主导模态形成的单向闭环对BDTI波动信息进行链路传递的现象,在连续3个月出现某种波动变化时,对未来2~3个月内的运价波动趋势提前做好运力管控和风险规避。
虽然BDTI的波动状态呈正常升降较为明显,但也不能小觑发生异常波动的现象,对于油船运输企业而言,必要时可加大力度监督子航线运价波动情况、建立油船运价波动预警机制、研发运价波动监控系统、备妥航运金融风险衍生品、加快提升市场管理人才技能等。BDTI的波动传导不仅受自身内部规律影响,也受政治环境、全球经济贸易、突发事件、世界原油运输格局等外部因素影响,这需要油船运输企业时刻关注全球市场宏观环境变化,提高市场敏感性,深度探索外部环境带来的机遇和风险,及时做好船舶运力战略投放,以应对经营管理危机。
本文在已有文献的成果上利用较为前沿的复杂网络方法来探究BDTI的波动特征,但只是内部结构的探究,对其他外部因素如原油价格、不同油船船型租金水平、油船船队规模、油船闲置运力、油船交付量等引起的运价变动,还需要进一步深入研究。随着全球对碳减排的日益重视,船舶燃油将逐渐被氢能、液化天然气等清洁能源所代替,未来油运市场将面临一次全新的改革,因此油船运价的预测具有重要意义。
参考文献:
[1]LI J, PARSONS M G. Forecasting tanker freight rate using neural networks[J]. Maritime Policy & Management, 1997, 24(1): 930. DOI: 10.1080/03088839700000053.
[2]FAN S R, JI T Y,GORDON W, et al. Forecasting Baltic dirty tanker index by applying wavelet neural networks[J]. Journal of Transportation Technologies, 2013, 3(1): 6887. DOI: 10.4236/jtts.2013.31008.
[3]范永辉, 杨华龙, 张宝华. 基于灰色关联理论的油轮运价指数波动分析[J]. 大连海事大学学报, 2009, 35(4): 3034. DOI: 10.16411/j.cnki.issn10067736.2009.04.029.
[4]张倩, 曲晨蕊, 曾庆成. 基于经验模式分解的原油运价指数波动[J]. 中国航海, 2019, 42(1): 129134.
[5]計明军, 张海燕, 王清斌. 基于组合模型的油轮运价指数分析与预测[J]. 交通运输系统工程与信息, 2012, 12(1): 199204. DOI: 10.16097/j.cnki.10096744.2012.01.002.
[6]袁凡. 基于分位数回归的油轮运价指数VaR风险研究[J]. 港口经济, 2013(5): 3033.
[7]王军, 张丽娜. 基于广义自回归条件异方差模型的世界原油运价风险分析[J]. 上海海事大学学报, 2011, 32(2): 2024.
[8]匡海波, 冯文文. 油轮最优投资决策研究: 基于原油运价指数波动风险的分析与决策选择[J]. 价格理论与实践, 2018(6): 126129. DOI: 10.19851/j.cnki.cn111010/f.2018.06.032.
[9]刘婷婷, 林国龙, 王直欢, 等. 波罗的海原油和成品油油船运价指数多重分形特征[J]. 上海海事大学学报, 2016, 37(1): 7074. DOI: 10.13340/j.jsmu.2016.01.013.
[10]韩华漪, 钱斌, 王学锋. 基于MFDFA方法的国际油轮运价指数多重分形分析[J]. 重庆交通大学学报(自然科学版), 2014, 33(5): 128133. DOI: 10.3969/j.issn.16740696.2014.05.29.
[11]冯文文, 匡海波, 孟斌. 基于改进均值回归的波罗的海原油运价指数模型研究[J]. 中国管理科学, 2018, 26(5): 4050. DOI: 10.16381/j.cnki.issn1003207x.2018.05.005.
[12]ADLAND R, CULLINANE K. The nonlinear dynamics of spot freight rates in tanker markets[J]. Transportation Research Part E, 2006, 42(3): 211224.
[13]安海岗, 都沁军, 张永礼. 基于复杂网络的时间序列单变量波动幅度研究[J]. 系统科学与数学, 2015, 35(2): 158169.
[14]周洁. 基于耦合网络的油价波动规律及其影响因素研究[D]. 镇江: 江苏大学, 2020.
[15]汤霞, 匡海波, 郭媛媛, 等. 基于复杂网络的中国出口集装箱运价指数波动规律[J]. 交通运输系统工程与信息, 2020, 20(2): 2632. DOI: 10.16097/j.cnki.10096744.2020.02.005.
(编辑赵勉)
收稿日期: 20210401修回日期: 20210630
基金项目: 国家社会科学基金(20BJY177)
作者简介: 林舒暖(1998—),女,广东汕尾人,硕士研究生,研究方向为交通运输工程,(Email)229389623@qq.com;
张婕姝(1973—),女,四川自贡人,教授,博士,研究方向为交通运输规划与管理,(Email)jszhangsh@126.com
