考虑悬浮系统影响的高速磁悬浮列车牵引控制策略
2022-06-25朱进权葛琼璇孙鹏琨王晓新
朱进权 葛琼璇 张 波 孙鹏琨 王晓新
考虑悬浮系统影响的高速磁悬浮列车牵引控制策略
朱进权1,2葛琼璇1张 波1孙鹏琨1,2王晓新1
(1. 中国科学院电力电子与电气驱动重点实验室(中国科学院电工研究所) 北京 100190 2. 中国科学院大学 北京 100049)
常导电磁式高速磁悬浮列车采用长定子直线同步电机驱动,电机的励磁磁极同时也是悬浮电磁铁,车辆的牵引力和悬浮力存在严重的非线性耦合关系,运行过程中悬浮系统的调节会对牵引系统造成影响,引起牵引力波动。该文建立考虑悬浮系统影响的长定子直线同步电机数学模型,针对牵引力波动问题,提出一种基于磁链观测的控制策略,该策略基于扩展反电动势法来观测磁链,通过将磁链参数应用于速度环和电流环,在线调整定子q轴电流从而抑制由悬浮系统引起的低频牵引力波动。但该策略在低速时磁链观测存在误差、性能受限,在此基础上提出结合自抗扰和磁链观测的复合控制策略,通过扩张状态观测器补偿磁链观测误差以及其余扰动。硬件在环实验结果表明,该控制策略有效地抑制了悬浮系统影响造成的牵引力波动,提高了磁悬浮列车的抗负载扰动能力和系统动态性能。
高速磁悬浮列车 悬浮系统 牵引系统 扩展反电动势 自抗扰控制
0 引言
常导电磁式高速磁悬浮列车采用长定子(长初级)直线同步电机驱动,电机的励磁磁极(悬浮磁体可称为次级)安装在车体下方,定子铁心及其三相电枢绕组沿轨道安装,结构示意图如图1所示[1]。定子绕组通入三相对称交流电后将产生行波磁场,驱动装在车上的磁极做直线运动。电机的励磁磁极同时也是悬浮电磁铁,长定子与励磁磁极在气隙磁场作用下相互吸引,产生悬浮力,使列车悬浮在轨道上8~12mm。电磁式磁悬浮列车的悬浮系统是一个不稳定系统,需要对励磁磁极的励磁电流进行闭环控制,进而保证悬浮气隙稳定。高速磁悬浮列车的悬浮力和牵引力均由长定子直线电机产生,两者存在非线性耦合关系,受功角关系影响较大,在任意功角情况下,两者之中任何一个变量的调节势必会影响到另一变量[2]。文献[3]通过有限元仿真分析了不同功角下的长定子直线同步电机牵引力和悬浮力的变化情况,在定子电流和励磁电流幅值恒定情况下,当功角从0°变化到180°时,悬浮力一直减小,牵引力先增大再减小,功角为90°时,牵引力最大。
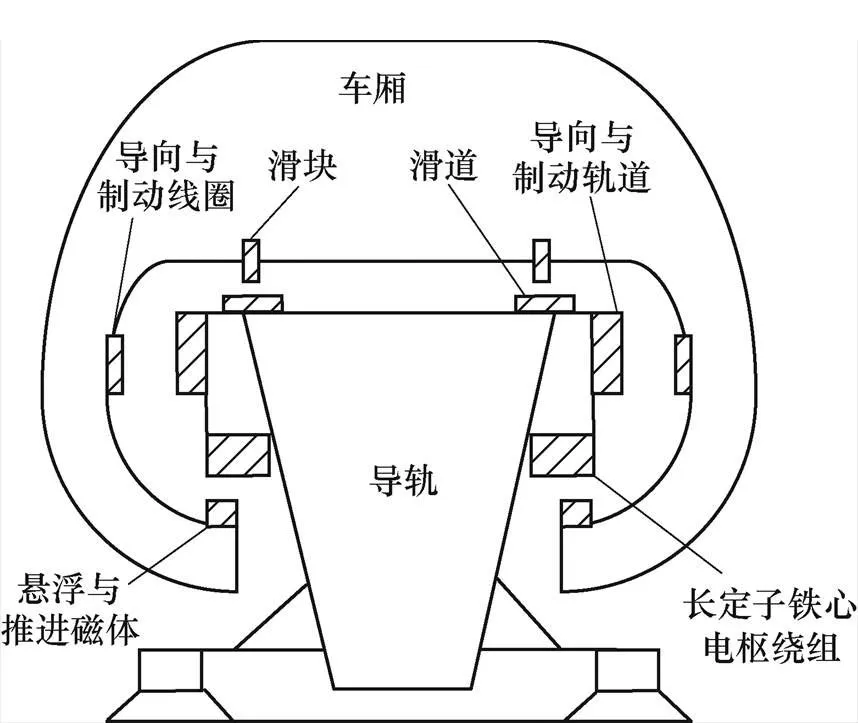
图1 常导电磁式磁悬浮列车的牵引、悬浮、导向系统结构示意图
为了实现牵引力和悬浮力的解耦控制,高速磁悬浮列车牵引用长定子直线同步电机多采用d=0(功角为90°)的转子磁场定向控制方式,此时电枢反应最小,使得牵引力与悬浮力耦合程度最小,可以通过调节定子电流q和励磁磁极的励磁电流分别控制牵引力和悬浮力[4]。目前大多数文献都是基于此原理将牵引控制器和悬浮控制器进行分开设计。对于牵引控制器,通过建立长定子直线同步电机在dq坐标系下的数学模型,采用转子磁场定向控制策略。为了精确地控制列车行驶的位置和速度,必须获得准确的位置信号[5]。但在实际的运行过程中,由于控制策略不同,或者位置测量不准,或者运行条件恶劣,常常定子电流的d≠0[6],此时气隙磁场会受影响,从而影响悬浮力和悬浮气隙。此外,在低开关频率牵引变流器供电条件下,电机定子电流的谐波分量也会影响牵引力和悬浮力,造成悬浮气隙波动[7]。
在悬浮控制器设计方面,国内外出现了许多非线性控制方法和现代分析方法,例如,自适应控 制[8]、滑模变结构控制[9]、神经网络控制[10]、模糊控制[11]等。悬浮控制算法解决的问题由最初的基本稳定提升到适应多参数变化和模型不确定,使悬浮控制器具有较好的自适应能力和鲁棒性。上述悬浮控制器的目的都是为了保持悬浮气隙的稳定,但对于实际运行的磁悬浮列车整个系统,负载扰动[12]、轨道的不平顺[13]以及垂直方向上的外力干扰[14],都将会引起悬浮气隙与励磁电流的变化,对牵引控制造成影响。此外,悬浮气隙的变化会造成电机自感、互感的变化,在运行过程中很难在线实时分析。
综上所述,磁悬浮列车牵引控制系统与悬浮系统之间的耦合是复杂的、非线性的。仅有少量文献同时考虑悬浮与牵引系统耦合关系,文献[15]建立了长定子直线同步电机的有限元分析模型,对其推力和悬浮力进行了分析,对位置传感器不准确和励磁电流波动引起的耦合效应进行了仿真和讨论。文献[16]分析了电枢电流变化时,励磁电流的有效调节范围。文献[17]基于磁链估计方法,抑制了悬浮系统引起的牵引力波动,但磁链观测存在误差时性能受限。为保障高速磁悬浮列车的稳定运行,必须考虑悬浮系统对牵引系统的影响,进而提出针对悬浮系统影响的鲁棒性好的牵引控制策略。
本文在考虑悬浮系统影响的前提下,以高速磁悬浮列车用长定子直线同步电机为研究对象,提出优化的牵引控制策略,在基于RT-Lab的高速磁悬浮半实物系统中进行硬件在环实验,验证了算法的正确性,在实际的高速磁悬浮线路应用中具有重要的实用价值。
1 考虑悬浮系统影响的长定子直线同步电机数学模型


式中,s为定子绕组有效匝数;为励磁线圈匝数;为电磁铁磁极有效面积;0为真空磁导率;()为悬浮气隙的高度。由于悬浮系统调节,磁悬浮列车通常稳定悬浮于额定气隙附近,气隙变化往往不大,而励磁电流变化较大,忽略D(),式(1)化简为
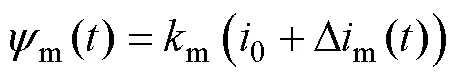
其中
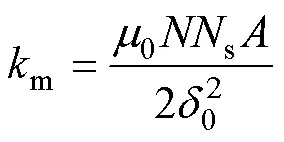
式中,0为额定气隙;0为额定电流;()=0+D();m()=0+Dm();而额定磁链为m0=m0。
高速磁悬浮列车悬浮系统是由多个磁极单元组成的多点悬浮系统,列车在实际运行过程中,各个悬浮控制点输出的励磁电流可能存在差别,因此考虑多点悬浮的磁链为

磁悬浮列车在双端供电模式下,采用两台变流器同时向定子绕组段供电,文献[6]推导了磁悬浮列车在双端供电模式下的数学模型,但没有考虑悬浮系统的影响,结合文献[6]和本文的分析,可以得到双端供电模式下考虑悬浮系统影响的长定子直线同步电机的电压方程以及牵引力方程为



从式(4)和式(5)可知,与传统的数学模型相比,励磁磁链不是恒定值,而是随悬浮系统实时变化,牵引力大小与励磁电流成正比,此外由悬浮系统引起的牵引力的波动Dx可以表示为

牵引力的波动幅值与磁链的波动幅值成正比,波动趋势与励磁电流近似相同,当列车加速时,牵引力波动幅值较大,匀速运行时波动幅值较小。
2 基于磁链观测的牵引控制策略
为了实现悬浮与牵引系统的解耦,长定子直线同步电机通常采用d=0的转子磁场定向控制方式,此时列车牵引力为

根据第1节分析可知,磁链m()受悬浮系统影响而变化,进而造成牵引力波动,若是可以估算到磁链的变化情况,及时调节q,则可以有效抑制由悬浮系统引起的牵引力波动。将式(4)中的电压方程变换到两相静止坐标系下,将所有包含电机角度的项整理到一起,可以将数学模型重写为

式中,α1、β1、α1、β1为第一台变流器输出电压和输出电流在ab坐标系下的分量;a2、b2、a2、b2为第二台变流器输出电压和输出电流在ab坐标系下的分量;x为扩展反电动势项,即
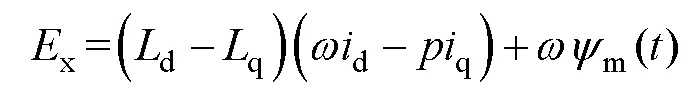
扩展反电动势项中包含了磁链信息,由于采用d=0控制,并且长定子直线同步电机漏感大,凸极效应不明显,动态过程中扩展反电动势与反电动势在幅值上略有差别,但在稳态时二者并无差别,因此可以根据观测的扩展反电动势来计算磁链。
长定子直线同步电机的扩展反电动势,可以通过构造观测器来获得,将电流的实际值与电流的观测值求差,再通过PI调节来观测扩展反电动势。文献[19]设计了磁悬浮列车在双端供电模式下的拓展反电动势观测器,在ab坐标系下对反电动势进行观测,其具体观测器表达式为


根据式(10)可以得到扩展反电动势的两个正交分量,因此利用正交锁相环估算电机的速度与角度,锁相环的原理为

式中,Dq 为角度差值;为直线电机转子角度的估计值;q 为直线电机转子角度的实际值。角度差值经过PI调节器处理后,得到转子角速度,对角速度进行积分运算,得到转子角度的估算值。综上所述,扩展反电动势观测器原理如图2所示。
获得扩展反电动势后,进而可以求得磁链的估算值为





综上所述,可以得到基于磁链观测的牵引控制策略控制框图如图3所示,速度环调节器的输出加上牵引力前馈值生成牵引力给定值,根据估算的磁链来计算电流给定值;对于电流内环,两台变流器的输出电流经过坐标变换以及求和后得到dq轴总电流,电流调节器的输出加上电流前馈值生成电压给定值,最终经过PWM产生开关信号,分别驱动两台变流器给长定子直线同步电机供电。通过将互感磁链参数应用于速度环和电流环,当磁链变大时,相应的减小电流;反之,亦然,在线调节定子q轴电流,从而抑制由悬浮系统引起的低频牵引力波动。
基于扩展反电动势法来观测磁链,虽然没有直接使用受悬浮系统影响的物理量,但由于观测器法固有的缺陷,在低速时反电动势观测不准确,此外运行过程中电机参数变化也会影响观测的精度,造成计算的磁链与真实的磁链存在偏差,因此基于磁链观测的方法虽然能在一定程度上削弱牵引力波动,但还是无法完全消除。
3 基于自抗扰和磁链观测的牵引控制策略
自抗扰控制器(Active Disturbance Rejection Control, ADRC)是一种对系统内扰和外扰鲁棒的控制器,不依赖数学模型[21]。自抗扰控制器的核心是扩张状态观测器(Extended State Observer, ESO),通过ESO实时估计系统的状态信息以及总扰动信息,并对扰动进行前馈补偿。本文在磁链观测的基础上引入自抗扰控制器,将两者相结合,通过扩展反电动势观测器实时计算磁链,计算的误差以及其余扰动通过ESO观测,并进行补偿,进而有效地抑制牵引力波动。
根据式(5),采用d=0控制,得到磁悬浮列车运动学方程为

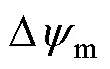

代入式(16)可得

式中,v为系统总扰动,包括磁链误差项以及未建模动态。对式(18)所述的一阶系统,构造二阶线性ESO,可得
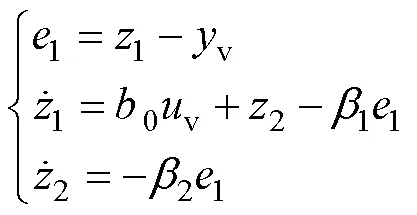
式中,0为系统增益,令0v;1、2为扩张状态观测器系数;1为的观测值;2为总扰动v的观测值;为最终的控制输入。
将式(19)化简后进行拉普拉斯变换可得

式中,系统的特征多项式为()=1+2,为典型的二阶系统,有两个极点,根据经典控制理论的劳斯判据,只要满足1>0、2>0,特征方程的根位于s域左半平面,系统就能稳定,误差呈指数衰减,最终趋于零。
将式(19)和式(20)相减,化简可得到总扰动观测值2与系统实际扰动v之间的扰动传递函 数为


选择比例反馈控制规律为

图4 扰动传递函数伯德图
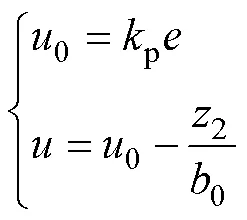
在观测器参数设计良好的情况下,可以认为2≈v,代入式(18)中得到

可以看出,自抗扰控制器将运动学方程中的磁链波动项以及未建模部分当做系统的总扰动,然后通过ESO进行实时估计总扰动,并给予补偿,补偿后,输出只和输入有关,从而达到对速度的良好跟踪以及抑制牵引力波动的目的。综上所述,可以得到基于自抗扰和磁链观测的牵引控制框图如图5所示。

图5 基于自抗扰和磁链观测的牵引控制框图
4 实验验证和结果分析
为了验证本文所提出的控制策略的有效性,搭建了基于RT-Lab的高速磁悬浮半实物实验平台如图6所示,由RT-Lab测试系统和牵引控制系统组成。RT-Lab测试系统包括四套24MV·A高功率变流器仿真子系统和一套直线电机仿真子系统,其中每台FPGA仿真机对应一套高功率变流器仿真子系统[22]。表1给出了长定子直线同步电机的主要参数。

图6 高速磁悬浮牵引半实物系统
表1 长定子直线电机参数

Tab.1 Long stator linear motor parameters
利用表1的参数,进行了硬件在环实验。下文为了便于描述,将传统的控制策略称为控制策略Ⅰ,将基于磁链观测补偿的控制策略称为控制策略Ⅱ,将基于自抗扰和磁链观测补偿的控制策略称为控制策略Ⅲ。作为跟踪性能和抗噪声能力之间的权衡,ESO的带宽选择为100Hz。表2列出了这三种控制方案的转速调节器参数。
表2 转速调节器参数

Tab.2 Parameters of speed regulator
为了验证基于扩展反电动势的磁链观测性能,在不考虑悬浮系统影响的情况下进行了硬件在环实验。图7为基于扩展反电动势的无传感器策略磁链观测波形。可以看出,提出的策略具有良好的速度估计精度,整个过程的速度估计误差不超过8m/s。由于反电动势的幅值在低速时太小而无法准确观测,因此估计的磁链在低速区域不准确。除此以外,估算磁链可以在中高速区域良好地跟踪实际的磁链。

图7 基于扩展反电动势的无传感器策略磁链观测波形
通过第1节的分析,磁链随悬浮系统励磁电流的调节而变化,进而引起牵引力的波动。为了验证所提出的控制方案的有效性,在考虑悬浮系统的影响下对几种控制策略的性能进行了比较,图8和图9分别为在磁链存在低频扰动下的高速和低速实验波形,磁链可以表示为m()=m0(1+0.1sin(10p))。

图8 三种控制策略在磁链波动干扰下的高速实验波形
从三种控制策略的实验结果来看,很明显,控制策略Ⅰ无法抑制悬浮系统引起的牵引力波动,整个过程中推力波动大于30kN。在高速区域,控制策略Ⅱ和Ⅲ都可以通过快速调节q轴电流显著地减小牵引力波动,而控制方案Ⅲ的效果更好,在补偿磁链计算误差的同时补偿其余扰动的影响,牵引力波动最小,不超过5kN。在低速区域,两种策略之间存在明显区别,策略Ⅱ不起作用,因为估算的磁链定值m0代替。但是控制策略Ⅲ通过扩张状态观测器估算出总扰动,进行前馈补偿,进而通过调节电流抑制牵引力波动,在低速仍然有效。

图9 三种控制策略在磁链波动干扰下的低速实验波形
磁悬浮车辆始终在恶劣的室外环境中运行,容易受到干扰的影响,图10为磁悬浮列车在匀加速过程中受到磁链阶跃扰动的实验波形,磁链m()阶 跃变化,其变化范围为m0到1.2m0,加速度为0.6m/s2。从实验结果可知,在没有扰动作用时,三种控制方案可以通过调节定子电流q来有效地控制牵引力。控制策略Ⅱ和Ⅲ在阶跃扰动后都能使牵引力保持在5kN的波动范围内,而控制策略Ⅲ在阶跃变化时具有较好的动态性能,牵引力冲击较小,因为磁链估计误差和外部扰动被看作系统的集总扰动,然后通过ESO进行及时估计,并进行前馈补偿。

图10 三种控制策略在磁链阶跃干扰下的加速实验波形
5 结论
针对高速磁悬浮列车受悬浮系统影响造成的牵引力波动问题,提出了一种基于自抗扰和磁链观测的控制策略。该控制策略通过磁链观测器实时观测磁链,观测误差和其余扰动通过自抗扰控制器进行补偿,达到对速度的良好跟踪以及抑制牵引力波动的目的。通过理论分析和硬件在环实验,所提出的控制策略能有效地抑制牵引力波动,改善了速度环的动态跟随性能、稳态性能以及抗干扰性能。
[1] Hellinger R, Mnich P. Linear motor-powered transpor- tation: history, present status, and future outlook[J]. Proceedings of the IEEE, 2009, 97(11): 1892-1900.
[2] 章九鼎, 卢琴芬. 长定子直线同步电机齿槽效应的计算与影响[J]. 电工技术学报, 2021, 36(5): 964- 972.
Zhang Jiuding, Lu Qinfen. Calculation and influences of cogging effects in long-stator linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 964-972.
[3] 饶健. 高速磁悬浮列车的牵引力与悬浮力的耦合特性分析[D]. 北京: 中国科学院电工研究所, 2018.
[4] 吕刚. 直线电机在轨道交通中的应用与关键技术综述[J]. 中国电机工程学报, 2020, 40(17): 5665-5675.
Lü Gang. Review of the application and key tech- nology in the linear motor for the rail transit[J]. Proceedings of the CSEE, 2020, 40(17): 5665-5675.
[5] 孙鹏琨, 葛琼璇, 王晓新, 等. 基于降阶观测器的高速磁浮列车无速度传感器控制算法[J]. 中国电机工程学报, 2020, 40(4): 1302-1309.
Sun Pengkun, Ge Qiongxuan, Wang Xiaoxin, et al. Sensorless control strategy of high-speed maglev based on reduced order observer[J]. Proceedings of the CSEE, 2020, 40(4): 1302-1309.
[6] 朱进权, 葛琼璇, 孙鹏琨, 等. 基于自抗扰的高速磁浮列车牵引控制策略[J]. 电工技术学报, 2020, 35(5): 1065-1074.
Zhu Jinquan, Ge Qiongxuan, Sun Pengkun, et al. Traction-system research of high-speed maglev based on active disturbance rejection control[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(5): 1065-1074.
[7] Lu Ganyun, Chong Haozhong, He Weiguo, et al. Harmonic analysis of the PWM inverter fed LSM drive system in the TRANSRAPID Shanghai[C]// 2003 Sixth International Conference on Advances in Power System Control, Operation and Management, Shanghai, China, 2003, 2: 547-557.
[8] Sun Yougang, Qiang Haiyan, Xu Junqi, et al. Internet of things-based online condition monitor and improved adaptive fuzzy control for a medium- low-speed maglev train system[J]. IEEE Transactions on Industrial Informatics, 2020, 16(4): 2629-2639.
[9] Chen Chen, Xu Junqi, Ji Wen, et al. Sliding mode robust adaptive control of maglev vehicle’s nonlinear suspension system based on flexible track: design and experiment[J]. IEEE Access, 2019, 7: 41874-41884.
[10] 陈琛, 徐俊起, 倪菲, 等. 基于人工智能负载估计系统的磁浮列车垂向振动主动控制[J]. 同济大学学报(自然科学版), 2020, 48(9): 1344-1352.
Chen Chen, Xu Junqi, Ni Fei, et al. Active control of vertical vibration for maglev train based on artificial intelligence load estimation system[J]. Journal of Tongji University (Natural Science), 2020, 48(9): 1344- 1352.
[11] Wai Rong-Jong, Lee Jeng-Dao. Robust levitation control for linear maglev rail system using fuzzy neural network[J]. IEEE Transactions on Control Systems Technology, 2009, 17(1): 4-14.
[12] 徐俊起, 林国斌, 陈琛, 等. 负载扰动下磁浮车辆多点悬浮建模与控制[J]. 同济大学学报(自然科学版), 2020, 48(9): 1353-1363.
Xu Junqi, Lin Guobin, Chen Chen, et al. Modeling and control of multi-point levitation of maglev vehicleunder loading disturbance[J]. Journal of Tongji University (Natural Science), 2020, 48(9): 1353-1363.
[13] 余佩倡, 李杰, 周丹峰, 等. 磁浮轨道不平顺对悬浮系统影响的抑制方法[J]. 国防科技大学学报, 2016, 38(4): 191-198.
Yu Peichang,Li Jie,Zhou Danfeng, et al. Method for suppressing influence of track irregularity to maglev suspension system[J]. Journal of National University of Defense Technology, 2016, 38(4): 191-198.
[14] 丁叁叁, 姚拴宝, 陈大伟. 高速磁浮列车气动升力特性[J]. 机械工程学报, 2020, 56(8): 228-234.
Ding Sansan, Yao Shuanbao, Chen Dawei. Aerodyna- mic lift force of high-speed maglev train[J]. Journal of Mechanical Engineering, 2020, 56(8): 228-234.
[15] Rao Jian, Wang Ke. Study on dynamic coupling characteristics of thrust and levitation force of long stator linear synchronous motor for maglev train[C]// 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, 2017: 1-4.
[16] Lu Bing, Tan Xiaodong, Li Qing, et al. The analysis of excitation current changes in long stator linear synchronous motor of maglev[C]//2014 Prognostics and System Health Management Conference (PHM- 2014 Hunan), Zhang Jiajie, China, 2014: 410-413.
[17] Wang Boyu, Wang Ke. A novel propulsion control scheme of long stator linear synchronous motor for maglev vehicle considering the influence of suspen- sion system[C]//2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 2018: 1481-1485.
[18] Sun Yougang, Xu Junqi, Qiang Haiyan, et al. Adaptive neural-fuzzy robust position control scheme for maglev train systems with experimental veri- fication[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(11): 8589-8599.
[19] 孙鹏琨, 葛琼璇, 王晓新, 等. 磁悬浮列车在双端供电模式下的无速度传感器控制[J]. 电工技术学报, 2018, 33(18): 4249-4256.
Sun Pengkun, Ge Qiongxuan, Wang Xiaoxin, et al. Research on speed sensorless control of maglev train with double-end power supply[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4249-4256.
[20] 刘金鑫, 葛琼璇, 王晓新. 高速磁浮牵引控制系统半实物实验研究[J]. 电工技术学报, 2015, 30(14): 497-503.
Liu Jinxin, Ge Qiongxuan, Wang Xiaoxin, et al. Hardware-in-loop research of traction-system for high-speed maglev[J]. Transactions of China Electro- technical Society, 2015, 30(14): 497-503.
[21] Han Jinqin. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Elec- tronics, 2009, 56(3): 900-906.
[22] 孙鹏琨, 葛琼璇, 王晓新, 等. 基于硬件在环实时仿真平台的高速磁悬浮列车牵引控制策略[J]. 电工技术学报, 2020, 35(16): 3426-3435.
Sun Pengkun, Ge Qiongxuan, Wang Xiaoxin, et al. Traction control strategy of high-speed maglev train based on hardware-in-the-loop real-time simulation platform[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3426-3435.
Traction Control Strategy of High-Speed Maglev Considering the Influence of Suspension System
1,2111,21
(1. Key Laboratory of Power Electronics and Electric Drive Institute of Electrical Engineering Chinese Academy of Sciences Beijing 100190 China 2. University of Chinese Academy of Sciences Beijing 100049 China)
The electromagnetic suspension (EMS) type high-speed maglev vehicleis driven by the long-stator linear synchronous motor. The excitation magnetic poles of motor areal so the electromagnets of suspension system, thus there is a serious nonlinear coupling relationship between the traction and levitation force of vehicle. The adjustment of the suspension system during operation will affect the traction system, which leads to traction force fluctuations. In this paper, a mathematical model of linear synchronous motor considering the influence of the suspension system is established. Aiming at the problem of traction fluctuations, a control strategy based on flux observation is proposed, which uses the extended electromotive force (EEMF) method to observe the flux. By applying the flux parameter to the speed loop and current loop, the q-axis current can be adjusted online to suppress the low-frequency traction fluctuation caused by the suspension system. However, the performance of this strategy is limited when the flux observation error exists at low speed region. Accordingly, a composite control strategy combining active disturbance rejection and flux observation algorithm is proposed, which compensates the flux observation error and other disturbances through the extend state observer (ESO). The results of hardware-in-the-loop (HIL) experiments show that the control strategy effectively suppresses the traction fluctuation caused by the influence of the suspension system, and improves the anti-load disturbance ability and dynamic performance.
High-speed maglev, suspension system, traction system, electromotive force, active disturbance rejection control
10.19595/j.cnki.1000-6753.tces.210471
TM359.4
朱进权 男,1993年生,博士研究生,研究方向为高性能电机牵引控制技术。E-mail: zhujinquan@mail.iee.ac.cn
葛琼璇 女,1967年生,研究员,博士生导师,研究方向为高压大功率变流器控制技术、高性能电机牵引控制技术。E-mail: gqx@mail.iee.ac.cn(通信作者)
国家重点研发计划(2016YFB1200602-20)和国家自然科学基金青年基金(51907188)资助项目。
2021-04-06
2021-05-15
(编辑 陈 诚)
