计及热阻与发射极电感匹配的并联IGBT芯片稳态结温均衡方法

范迦羽 郑飞麟 王耀华 李学宝 崔 翔

计及热阻与发射极电感匹配的并联IGBT芯片稳态结温均衡方法

范迦羽1郑飞麟1王耀华2李学宝1崔 翔1

（1. 新能源电力系统国家重点实验室（华北电力大学）北京 102206 2. 先进输电技术国家重点实验室（全球能源互联网研究院有限公司）北京 102209）

在大量芯片并联的IGBT器件内部，热阻和发射极寄生电感是决定芯片稳态结温分布的关键参数。因此，合理设计芯片并联支路的热阻和发射极寄生电感，对均衡并联芯片的稳态结温非常重要。为此，该文首先建立两IGBT并联芯片的电热模型，研究并联IGBT芯片动态损耗与结温、发射极寄生电感之间的规律。并通过瞬态电热耦合计算，研究热阻和发射极寄生电感对并联芯片结温分布的影响。在此基础上，提出计及热阻与发射极电感匹配的并联IGBT芯片稳态结温均衡方法，可通过联立方程得到热阻或发射极寄生电感的参考值，从而避免复杂的电热瞬态计算。最后以两IGBT并联芯片为例，给出不同工作频率下并联芯片的稳态结温，表明了该文所提稳态结温均衡方法的有效性。

并联IGBT芯片 热阻 发射极寄生电感 稳态结温均衡方法

0 引言

为满足高压柔性装备的功率需求，绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor, IGBT）芯片常被大规模并联使用[1]。而芯片并联回路寄生电感、热阻等封装参数的差异，会引起并联芯片的稳态结温分布不均[2-3]。若器件长期工作在此环境下，不仅会影响封装材料的使用寿命和绝缘材料的绝缘性能[4]，也会加速芯片的老化[5-6]。工程中往往采用降额运行的方法，以减小并联芯片稳态结温不均对柔性装备的危害，导致器件性能没有得到充分发挥。因此，并联IGBT芯片的稳态结温分布不均，已经成为了高压柔性装备功率密度和可靠性提升亟待解决的关键问题。

目前，国内外学者针对器件内部并联芯片的稳态结温开展了大量理论和实验工作。2020年，华北电力大学的Zhang Yiming等提出了时序电参数法，研究了压接型IGBT器件内部芯片的稳态的结温分布[7]。研究表明，在低频换相时，影响器件内部稳态结温分布的主要因素是芯片通态管压降和各芯片散热支路的热阻。

与低频工况不同，当IGBT器件工作在中高频工况时，随着器件工作频率的升高，影响并联IGBT芯片换相损耗的关键参数变为芯片各支路的发射极寄生电感和封装热阻。2015年，ABB公司的Chen Nan等研究了IGBT器件汇流母排结构对器件开关损耗的影响[8]。之后，华北电力大学的顾妙松等提出，汇流母排的空间布局会影响各芯片支路发射极寄生电感，从而引起IGBT器件内部并联芯片的动态不均流[9]。2020年，华北电力大学的Zhang Yiming等研究了压接型IGBT器件的热网络模型，与实验的温升结果有很好的一致性[10]。在实际换相运行中，器件的发射极寄生电感和封装热阻共同决定了并联IGBT芯片的稳态结温分布。2017年，浙江大学的Tang Yunyu等研究了并联IGBT器件的寄生电感和热阻对器件并联器件损耗的影响[11]，其研究表明，并联器件的稳态结温差会因封装寄生电感不同而出现显著差异。

但由于并联IGBT芯片复杂的损耗特性，且受限于测量手段，大部分学者通常采用仿真的方法研究中高频工况下并联IGBT芯片的稳态结温分布问题。1997年，A. Analogy公司的A. Mantooth等提出了IGBT器件的瞬态电热耦合模型[12]，A. Mantooth的工作结合了A. Hefner提出的IGBT芯片电热模型[13]，与器件封装的Cauer热网络模型[14]，系统研究了IGBT器件封装参数对器件换相运行的影响。此后，这类电热耦合模型被广泛地应用于IGBT器件的换相过程分析[15]。但是，器件的换相过程在微秒时间尺度，而器件的热时间常数则为几秒甚至十几秒。器件热时间常数随其功率等级的不断增加，瞬态电热模型存在效率低、计算速度慢的问题，浪费了大量计算资源。

此外，在中高频工况下，并联芯片结温分布不均带来的危害也更大。一方面，并联芯片电流分配不均会危害到器件的安全工作区，导致器件的过电流失效[16]；另一方面，电流不均引起的损耗差异，会导致并联芯片的稳态结温不同，限制器件的最大工作电流，从而降低器件的功率密度与短路电流承受能力[17-18]。所以，在器件封装设计时应权衡考虑并联器件的电流均衡和温度均衡问题，本文重点关注并联IGBT芯片动态不均流对其稳态结温分布的影响。

因此，为实现并联IGBT芯片的稳态结温的均衡调控，并改善瞬态电热仿真方法计算速度慢的问题，本文首先利用并联IGBT芯片电热模型，研究了并联各芯片动态损耗与结温、发射极寄生电感的关系，并分析了热阻和发射极寄生电感对并联芯片稳态结温的影响。而后提出了并联IGBT芯片稳态结温均衡方法，通过联立方程得到芯片热阻和发射极寄生电感的参考值，从而避免了复杂的电热耦合计算。最后以并联两IGBT芯片为例，文中给出了不同工作频率下热阻和发射极寄生电感的匹配关系，展示了本文方法的有效性。

1 并联IGBT芯片的动态损耗特性

1.1 并联芯片损耗的影响因素

IGBT芯片作为温敏元件，其电气参数受芯片结温影响很大，如IGBT芯片的通态管压降、栅极阈值电压和跨导等参数。工程中，通常建立IGBT芯片的行为模型如图1所示，以研究芯片损耗和芯片外部换相条件（直流母线电压、负载电流、温度）的关系。

图1 IGBT芯片的行为模型

图1中，ge、gc、ce分别为IGBT芯片栅-射极、栅-集极、集-射极间的电容，IGBT的极间电容受直流母线电压影响较大，在不同温度下变化可忽略不计。除此之外，g为IGBT芯片串联的栅极内阻，b为IGBT芯片的基区等效电阻，用以等效IGBT通态时的电导调制效应。mos和p分别为IGBT芯片的沟道电流和空穴电流，可以反映IGBT器件的转移特性和输出特性。

在不同温度点下，通过设置不同的栅极电阻、基区等效电阻、跨导、栅极阈值电压、通态管压降、电流放大倍数等参数，可以仿真得到IGBT芯片的换相特性。同时，通过插值法建立芯片电气参数与温度的数学关系，可模拟IGBT芯片结温上升过程中芯片的电气特性。因此，当并联IGBT芯片工作在不同结温下时，上述芯片参数的不同会引起芯片的动态不均流，从而导致并联芯片的动态损耗不同。

在IGBT器件的内部，并联的IGBT芯片由汇流母排和绑定线等金属导体实现电气连接。在IGBT器件的开关过程中，这些金属导体的寄生电感对并联IGBT的换相过程影响很大。尤其当并联芯片的发射极寄生电感不同时，并联芯片的栅-射极电压也不同，从而影响并联芯片的动态损耗。为研究发射极寄生电感对并联芯片损耗特性的影响，在IGBT芯片行为模型的基础上，建立两IGBT并联芯片等效电路模型如图2所示。

图2 两IGBT并联芯片的等效电路模型

图2展示了两IGBT并联芯片的等效电路，图中，load为续流二极管并联负载电感。cc和gate分别为IGBT器件的直流母线电压和栅极驱动电压。g1和g2分别为并联芯片IGBT1和芯片IGBT2的驱动栅极电阻。bus为IGBT器件中集电极汇流母排的寄生电感，c1和c2为各并联芯片集电极支路的寄生电感。同理，e1和e2为各并联芯片发射极支路的寄生电感。表1列出了并联IGBT芯片电路模型中的部分参数。在表1中，驱动栅极电阻g1和g2均为20W，母排的寄生电感bus=40nH，集电极寄生电感c1=c2=20nH。

表1 并联IGBT芯片电路模型中部分参数

Tab.1 Partial parameters in parallel IGBT chips model

并联IGBT芯片的发射极寄生电感e不仅会因器件内部的封装布局不对称而不同，且器件外部的汇流母排对器件发射极支路的互感不同也会导致并联芯片的动态不均流。当并联芯片的发射极寄生电感不同时，会直接影响到各并联芯片的栅-射极电压。所以，其对并联芯片换相过程的影响需要关注[19]。

1.2 并联芯片动态损耗的拟合公式

当IGBT器件在实际运行时，由于其内部封装布局的不对称，并联的芯片的损耗同时受温度和发射极寄生电感的影响。在两IGBT芯片并联的等效电路模型中，并联芯片的直流母线电压1.5kV，总负载电流100A。当芯片IGBT2的发射极寄生电感e2=20nH时，图3利用并联IGBT芯片的等效电路模型研究了IGBT芯片动态损耗的影响因素，并给出了动态损耗和温度、发射极寄生电感的关系。

图3 并联IGBT芯片动态损耗与结温和发射极寄生电感的关系

图3中，并联芯片的动态损耗随芯片结温的升高而增加。图3a中，由于寄生电感影响芯片的开关速度，芯片IGBT1的动态损耗随着e1的增加而减小。当并联芯片工作在25℃，e1=20nH时，芯片IGBT1的动态损耗为70mJ；当e1=50nH时，芯片IGBT1的动态损耗减小至62mJ。对应地，芯片IGBT2的动态损耗随e1的增加而增加。当并联芯片工作在100℃，e1=20nH时，芯片IGBT2的动态损耗为82mJ；当e1=50nH时，动态损耗达到了96mJ。

综上所述，可得芯片IGBT1的动态损耗的拟合表达式为

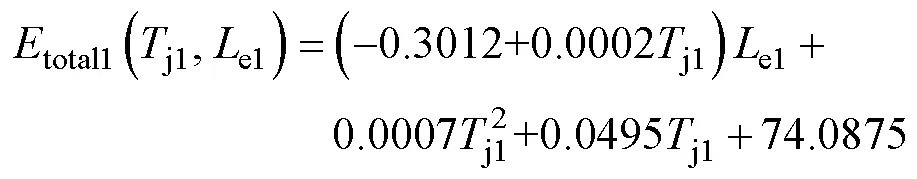
同理，芯片IGBT2动态损耗的拟合表达式为

并联芯片动态损耗的拟合结果与计算结果的对比见附表1和附表2。拟合式（1）、式（2）和图3中结果的最大相对误差在3%以内，验证了拟合公式的有效性。

不同温度下并联IGBT芯片的动态损耗是IGBT芯片重要的特性，决定了中高频工况下并联芯片的稳态结温分布。实际工程中，根据动态损耗拟合表达式（1）、式（2），不仅有助于分析IGBT芯片的电热特性，也可以为芯片的封装设计提供参考。

2 热阻与发射极寄生电感对并联芯片稳态结温的影响

在中高频工况下，并联芯片的稳态结温分布主要取决于芯片的动态损耗和封装热阻。如第1节所述，在换相过程中，由于测量手段受限，难以研究芯片的动态损耗与封装寄生电感和热阻间复杂的关系。因此，研究人员通常建立IGBT芯片的瞬态电热耦合模型开展并联芯片稳态结温的研究。

2.1 瞬态电热耦合仿真方法

瞬态IGBT芯片的电热耦合仿真方法将第1节中介绍的IGBT芯片的电热模型和热网络模型结合，进行电热的实时仿真计算。一方面芯片的换相损耗作为热路模型的热源；另一方面封装的热容热阻参数也决定了芯片的运行结温。图4给出了两IGBT芯片并联的瞬态电热耦合仿真原理[11]。

图4 并联IGBT芯片电热模型原理

图4中，瞬态IGBT芯片的电热耦合模型，被广泛应用于IGBT芯片和器件的连续换相运行分析。并联IGBT芯片的电热模型由电路模型和热路模型两部分组成。电路模型部分中，并联芯片的换相条件（直流母线电压、负载电流、工作频率等）、并联芯片电路参数（栅极电阻、各支路寄生电感等）和IGBT芯片参数（芯片结温、通态管压降、阈值电压等）决定了芯片在换相中的损耗功率loss1和loss2。热路模型部分，IGBT芯片作为封装热网络的热源，其芯片结温温度由芯片发热功率和芯片散热路径的热容热阻决定。

在IGBT芯片瞬态电热耦合仿真模型中，通过电路模型计算得到给定条件下时刻并联IGBT芯片的动态损耗功率，并结合并联芯片的封装热容热阻参数，得到+D时刻IGBT芯片的结温。随着芯片升温时间逐渐增加，热容对芯片结温的影响变小，芯片最终运行在稳态结温。

所以，不论是并联芯片封装热阻导致的芯片结温不同，还是并联芯片各支路的寄生电感差异，都会引起并联芯片的动态不均流，从而影响并联芯片的稳态结温分布。

2.2 并联芯片稳态结温的影响因素研究

当并联芯片的发射极寄生电感e1和e2均为20nH，芯片IGBT1的封装热阻thjc1=0.573℃/W，芯片IGBT2的封装热阻thjc2=0.742 3℃/W时，设置计算起始温度为25℃。根据瞬态电热耦合模型得到的并联芯片的稳态结温分布如图5所示。

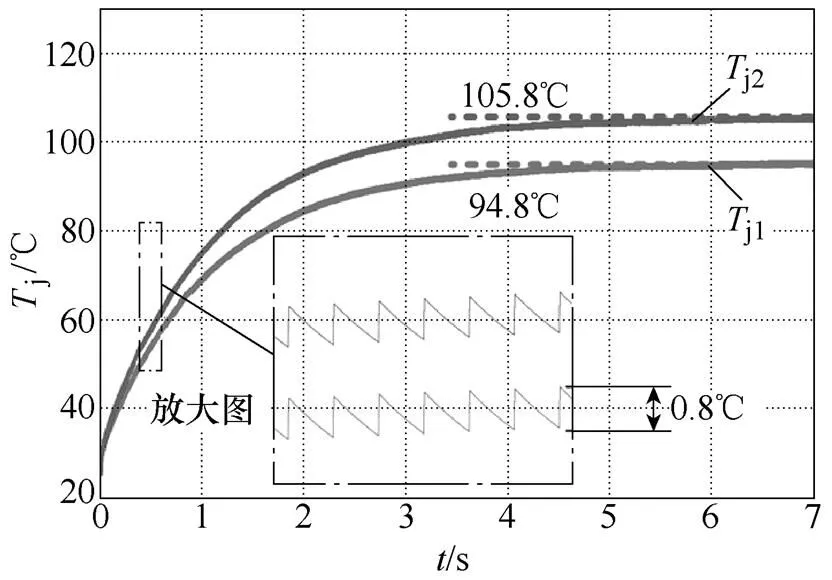
图5 不同热阻对并联芯片稳态结温的影响

图5中，由于封装中热容参数的影响，并联芯片的结温在约5s后达到稳定。当封装热阻相差30%，芯片的工作频率为1.25kHz时，芯片IGBT1的结温稳定在94.8℃，而芯片IGBT2的结温则稳定在105.8℃，最终并联芯片的稳态结温差达到了11℃。从放大图中可知，因为热容的储热效应，器件在每次换相过程中，都存在0.8℃左右的温度波动。由此可知，当并联器件的寄生电感参数相同时，封装热阻更大的芯片将具有更高的动态损耗，同时将工作在更高的结温下。

类似地，当并联芯片的封装热阻都为0.573℃/W，芯片IGBT2的发射极寄生电感e2=20nH时，不同发射极寄生电感e1对芯片IGBT2的稳态结温的影响如图6所示。

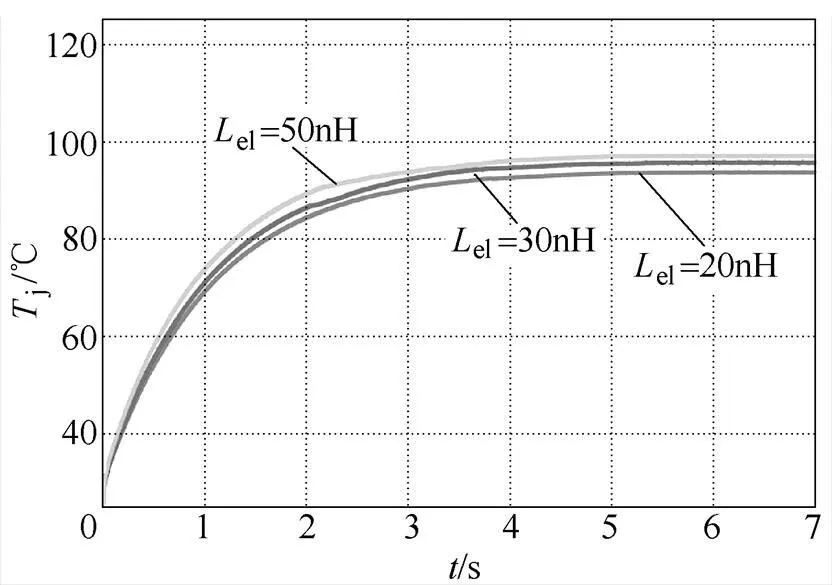
图6 不同发射极寄生电感Le1对芯片IGBT2结温的影响

图6中，设置计算的初始温度为25℃，当并联芯片的发射极寄生电感e1=20nH时，并联芯片的稳态结温为94.1℃，随着芯片IGBT1的发射极寄生电感e1不断增加，芯片IGBT2的稳态结温也会因芯片动态损耗的增加而略有增加。当e1=50nH时，芯片IGBT2的稳态结温为97.5℃。由此可见，发射极寄生电感e1引起的动态不均流虽会导致芯片IGBT2动态损耗功率loss2的增加，并且导致芯片IGBT2的稳态结温升高。但在并联芯片封装热阻相同的情况下，不同发射极寄生电感对并联芯片间的最高稳态结温的影响较小。

器件实际运行中，发射极寄生电感和热阻共同影响并联芯片的稳态结温，图7给出了在封装热阻不同时，发射极寄生电感对并联IGBT芯片稳态结温的影响。

图7 封装参数不匹配时并联芯片的稳态结温分布

图7中，当并联芯片的封装热阻thjc2比thjc1高30%，发射极寄生电感e1和e2相同时，并联芯片的稳态结温差为11℃。随着芯片IGBT1发射极寄生电感e1的增加，芯片IGBT1的动态损耗功率loss1明显下降。因此，从图7中可知，芯片IGBT1的稳态结温会随着e1的增加而下降。芯片IGBT2的稳态结温随发射极寄生电感e1的增加而明显增加。同理，并联芯片的稳态结温差会随着发射极寄生电感差De的增大而增加。当De=30nH时，并联芯片的稳态结温差增大至22.3℃。

综上所述，通过并联IGBT芯片的瞬态电热耦合仿真可知，当并联芯片的封装热阻相同时，发射极寄生电感不同对芯片间的最高稳态结温影响不大。但当并联芯片封装热阻不同时，发射极寄生电感的差异会放大封装热阻造成的稳态结温差，且导致并联芯片间的最高结温大幅增加，进一步限制并联芯片的安全工作区。因此，在器件封装设计中，应首先尽可能保证器件的封装热阻一致。当器件的封装热阻不同时，也应避免封装热阻和发射极寄生电感的参数不匹配，以保证并联IGBT芯片稳态结温的均衡。

虽然瞬态电热耦合仿真方法通过结合IGBT芯片的电路模型和封装热容热阻的热网络模型，可被用于研究并联IGBT芯片和器件在实际换相运行时的电热特性。但是对于调控并联IGBT芯片的稳态结温而言，考虑热容储热效应的瞬态电热耦合仿真方法存在计算效率低、计算速度慢等问题。尤其当功率器件的热时间常数随其功率等级的增大而不断增加，这一矛盾更加尖锐。其核心在于，并联芯片动态损耗与封装热阻、发射极寄生电感间相互作用，其关系尚不明确。为此，本文通过建立热阻与发射极寄生电感匹配关系，提出了并联IGBT芯片的稳态结温均衡方法。

3 并联IGBT芯片稳态结温的均衡方法

3.1 并联芯片稳态结温的均衡方法

IGBT器件内部的封装热容主要影响IGBT芯片的升温过程，因此，并联IGBT芯片的稳态结温分布与热容无关。为研究并联IGBT芯片稳态结温和封装热阻、发射极寄生电感之间的关系，建立了并联IGBT芯片的等效热阻网络如图8所示。

图8中，loss1和loss2分别为芯片IGBT1和芯片IGBT2的动态损耗功率，j1和j2则为芯片IGBT1和芯片IGBT2的稳态结温，thjc1和thjc2为芯片IGBT1和芯片IGBT2的结到壳热阻。两只并联的IGBT芯片被放置于同一散热器上，heatsink为散热器热阻。

图8 并联IGBT芯片的等效热阻网络

本文重点关注芯片封装热阻thjc和发射极寄生电感e对并联芯片稳态结温j的影响。当并联的IGBT芯片工作在中高频工况下，此时芯片的升温主要取决于其动态损耗功率。因此，当IGBT2的发射极寄生电感e2为固定值时，散热器表面温度A、芯片结温和环境温度a之间的关系可表示为

将式（3）代入式（4）和式（5）中，可得

将式（5）减式（4）可得

从式（7）和第2节的瞬态仿真结果可知，当发射极寄生电感e1增加时，虽然芯片IGBT2的动态损耗功率loss2明显增加，但是并联芯片的总动态损耗功率却变化不大。因此，当并联芯片热阻相同时，发射极寄生电感对芯片的结温改变影响不大。同时，从式（8）可知，当并联IGBT芯片的封装热阻不同时，发射极寄生电感造成的芯片动态损耗差异会恶化并联芯片的稳态结温。一方面限制了芯片的性能；另一方面也不利于并联芯片长期可靠运行，因此，需要对并联芯片封装的热阻和寄生电感进行匹配。

当芯片IGBT1与芯片IGBT2的稳态结温均衡，且均为je时，式（8）可改写为

同时，并联IGBT芯片的动态损耗功率可以表示为

同理，可将式（7）改写为

将式（10）代入式（12）中，可得

由此，式（11）和式（13）得到了当保持并联芯片稳态结温均衡条件时，芯片动态损耗、发射极寄生电感e1和封装热阻的匹配关系。当并联芯片的动态损耗特性已知时，根据并联芯片的封装热阻thjc1、thjc2和heatsink，联立式（11）和式（13）即可得到不同频率下并联IGBT芯片封装寄生参数。当并联芯片的封装寄生电感已知时，同理，可以得到稳态结温均衡时匹配的发射极寄生电感。综上所述，可以通过解方程得到并联芯片封装的匹配参数，且此时并联芯片的稳定结温为je。所以，通过求解式（11）和式（13）可直接得到并联芯片的稳态结温和匹配的封装热阻或发射极寄生电感，从而实现并联芯片稳态结温的均衡。该方法通过拟合建立芯片动态损耗和结温、发射极寄生电感之间的关系。由于所提方法不考虑芯片升温过程及热容参数的影响，从而避免了复杂的瞬态电热耦合计算。

3.2 热阻和发射极寄生电感的匹配关系

从3.1节的分析可知，式（11）和式（13）建立了封装热阻和发射极寄生电感的匹配关系。根据本文提出的并联型芯片稳态结温的均衡方法，当并联IGBT芯片损耗的电热特性已知时，可以直接通过联立方程组解得并联芯片的热阻或发射极寄生电感，从而避免复杂的电热耦合计算。

以两IGBT芯片并联为例，将式（1）和式（2）代入式（11）和式（13）中，可联立方程得并联IGBT芯片稳态结温相同时的封装参数匹配关系。图9展示了0.6kHz频率下IGBT芯片封装热阻和发射极寄生电感的匹配关系。

图9 0.6kHz下寄生电感和热阻的参数匹配关系

当并联IGBT芯片的工作频率为0.6kHz时，图9中给出了匹配条件下发射极寄生电感随热阻的变化关系即对应的稳态均衡结温。当thjc1=0.573℃/W，芯片IGBT2的发射极寄生电感e2=20nH时，为保证并联IGBT芯片的稳态结温相同，芯片IGBT1的发射极寄生电感e1随着芯片IGBT2的热阻thjc2增加而增加。当thjc2=0.6℃/W，对应的发射极寄生电感e1=23.77nH，此时并联芯片的稳态结温为82.6℃。当thjc2=0.744 3℃/W时，为保证并联芯片结温相同，芯片IGBT1应匹配47nH的发射极寄生电感，对应的稳态结温为87.8℃。类似地，当并联IGBT芯片工作在0.7kHz频率的工况下时，其寄生电感和热阻的参数匹配关系和对应的稳态均衡结温如图10所示。

对比不同频率下的结果可知，随着芯片工作频率的升高，并联芯片的稳态结温也随之增加。当thjc2=0.657℃/W，芯片工作在0.6kHz时，并联芯片的稳态结温为84.76℃；当芯片工作在0.7kHz时，对应的稳态结温升高到96.53℃。相比于瞬态电热耦合计算方法，本文所提的并联芯片稳态结温均衡方法利用并联芯片动态损耗的电热特性，可以直接得到不同工作频率下寄生电感和热阻的参数匹配关系，避免了复杂的电热耦合计算。但需要注意的是，硅基IGBT芯片无法长期工作在125℃以上，且并联芯片的结温会随芯片工作频率的增加而增加。所以，当并联芯片的稳态结温高于125℃时，本文所提方法虽能给出寄生电感和热阻的匹配关系，却无太大参考意义[20]。

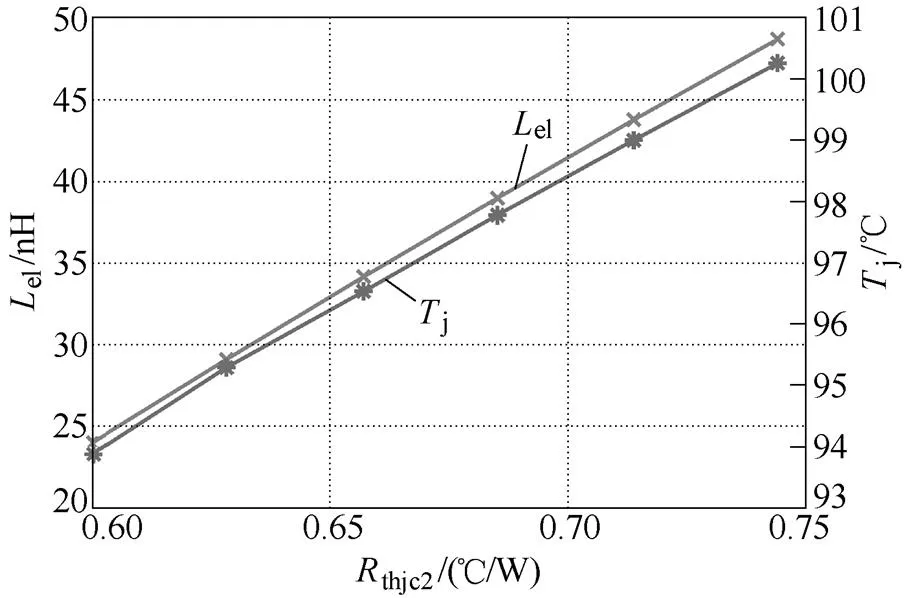
图10 0.7kHz下寄生电感和热阻的参数匹配关系

随着功率器件内部并联芯片数目的不断增加，传统电热仿真对于器件内部并联芯片稳态结温的改进是有限的。相比之下，根据并联芯片稳态结温建立的封装参数匹配关系，不仅可以节省大量计算资源，同时能更全面地优化器件的封装布局。因此，当并联芯片的封装热阻和寄生电感因空间布局无法保证相同时，利用本文所提方法可以优化并联芯片稳态的结温分布，从而提升器件的长期运行可靠性。

4 结论

本文主要研究了计及热阻与发射极寄生电感匹配的并联IGBT芯片稳态结温均衡的调控方法。主要结论如下：

1）建立了并联IGBT芯片的电热模型，研究了并联芯片结温、发射极寄生电感与并联芯片动态损耗的关系。提出并联芯片的动态损耗拟合公式，公式计算结果与模型结果的误差小于3%，具有很好的有效性。

2）获得了IGBT芯片的封装热阻、发射极寄生电感对并联芯片稳态结温的影响规律。结果表明，发射极寄生电感对并联芯片间的最高稳态结温影响较小，但当并联芯片封装热阻不同时，发射极寄生电感引起的动态不均流会恶化并联芯片的稳态结温分布，导致并联芯片间的最高结温大幅增加，进而限制并联芯片的安全工作区。

3）提出了并联IGBT芯片稳态结温均衡的方法。本文方法根据不同结温下并联IGBT芯片的动态损耗，通过联立方程组得到匹配的热阻和电感参数，实现了并联芯片稳态结温均衡。由于所提方法不考虑芯片升温过程及热容参数的影响，从而避免了复杂的IGBT瞬态电热耦合计算。

并联芯片IGBT1和IGBT2在不同条件下动态损耗的拟合结果和仿真计算结果对比见附表1和附表2。其中，拟合公式如式（1）和式（2）所示。

附表1 芯片IGBT1动态损耗计算值与拟合值对比

App.Tab.1 The comparsions of dynamic losses between the simluation results and fitting ones of IGBT1

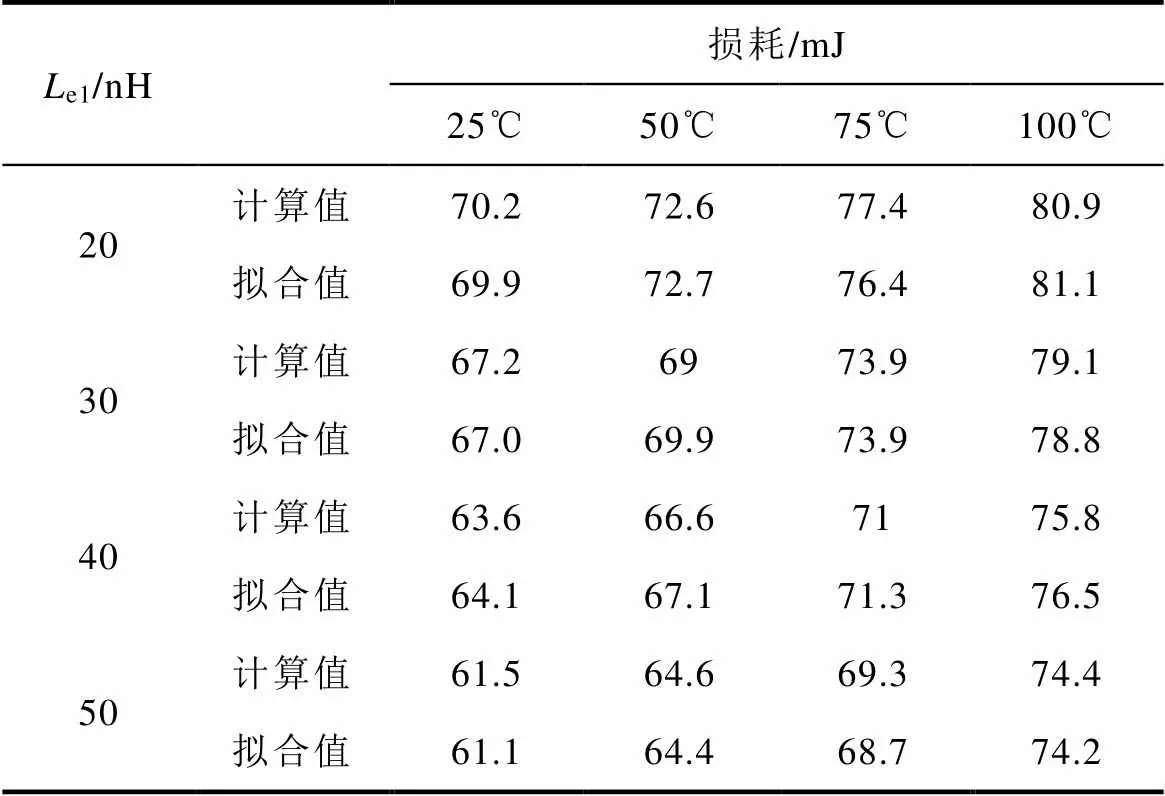
Le1/nH损耗/mJ 25℃50℃75℃100℃ 20计算值70.272.677.480.9 拟合值69.972.776.481.1 30计算值67.26973.979.1 拟合值67.069.973.978.8 40计算值63.666.67175.8 拟合值64.167.171.376.5 50计算值61.564.669.374.4 拟合值61.164.468.774.2

附表2 芯片IGBT2动态损耗计算值与拟合值对比

App.Tab.2 The comparsions of dynamic losses between the simluation results and fitting ones of IGBT2

Le1/nH损耗/mJ 25℃50℃75℃100℃ 20计算值70.272.677.480.9 拟合值70.773.477.081.5 30计算值77.778.582.686.8 拟合值76.578.882.186.3 40计算值82.584.887.391.0 拟合值82.384.287.191.0 50计算值87.789.292.195.6 拟合值88.189.792.295.8

从表中可知，拟合结果与芯片的动态损耗计算值有很好的一致性，其中最大相对误差小于3%，从而验证了拟合公式的有效性。

[1] Eicher S, Rahimo M, Tsyplakov E, et al. 4.5kV press pack IGBT designed for ruggedness and reliabi- lity[C]//2004 IEEE Industry Applications Conference, Seattle, 2004: 1534-1539.

[2] 邓二平. 压接型IGBT器件内部电-热-力多物理场耦合模型研究[D]. 北京: 华北电力大学, 2018.

[3] 陈宇, 周宇, 罗皓泽, 等. 计及芯片导通压降温变效应的功率模块三维温度场解析建模方法[J]. 电工技术学报, 2021, 36(12): 2459-2470.

Chen Yu, Zhou Yu, Luo Haoze, et al. Analytical 3D temperature field model for power module con- sidering temperature effect of semiconductor voltage drop[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2459-2470.

[4] 顼佳宇, 李学宝, 崔翔, 等. 高压大功率IGBT器件封装用有机硅凝胶的制备工艺及耐电性[J]. 电工技术学报, 2021, 36(2): 352-361.

Xu Jiayu, Li Xuebao, Cui Xiang, et al. Preparation process and breakdown properties of silicone gel used for the encapsulation of IGBT power modules[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 352-361.

[5] Wang Bo, Zhou Luowei, Zhang Yi, et al. Active junction temperature control of IGBT based on adjusting the turn-off trajectory[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 5811-5823.

[6] 张军, 张犁, 成瑜. IGBT模块寿命评估研究综述[J].电工技术学报, 2021, 36(12): 2560-2575.

Zhang Jun, Zhang Li, Cheng Yu. Review of the lifetime evaluation for the IGBT module[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(12): 2560-2575.

[7] Zhang Yiming, Deng Erping, Zhao Zhibin, et al. Sequentialce() method for the accurate measure- ment of junction temperature distribution within press-pack IGBTs[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 3735-3743.

[8] Chen Nan, Chimento F, Nawaz M, et al. Dynamic characterization of parallel-connected high-power IGBT modules[J]. IEEE Transactions on Industry Application, 2015, 51(1): 539-546.

[9] 顾妙松, 崔翔, 彭程, 等. 外部汇流母排对压接型IGBT器件内部多芯片并联均流特性的影响[J]. 中国电机工程学报, 2020, 40(1): 234-245.

Gu Miaosong, Cui Xiang, Peng Cheng, et al. Influence of the external busbar on current sharing performance inside a multi-chip press-pack IGBT device[J]. Proceedings of the CSEE, 2020, 40(1): 234-245.

[10] Zhang Yiming, Deng Erping, Zhao Zhibin, et al. A physical thermal network model of press pack IGBTs considering spreading and coupling effects[J]. IEEE Transactions on Components, Packaging and Manufa- cturing Technology, 2020, 10(10): 1674-1683.

[11] Tang Yunyu, Ma Hao. Dynamic electrothermal model of paralleled IGBT modules with unbalanced stray parameters[J]. IEEE Transactions on Power Electro- nics. 2017, 32(2): 1385-1399.

[12] Mantooth A, Hefner A. Electrothermal simulation of an IGBT PWM inverter[J]. IEEE Transactions on Power Electronics, 1997, 12(3): 474-484.

[13] Hefner A. A dynamic electro-thermal model for the IGBT[J]. IEEE Transactions on Industry Application, 1994, 30(2): 394-405.

[14] Hefner A, Blackburn D. Thermal component models for electrothermal network simulations[J]. IEEE Transa- ctions on Components, Packaging, and Manufacturing Technology, 1994, 17(3): 413-424.

[15] Luo Yifei, Xiao Fei, Liu Binli, et al. A physics-based transient electrothermal model of high-voltage press- pack IGBTs under HVDC interruption[J]. IEEE Transa- ctions on Power Electronics, 2020, 35(6): 5660- 5669.

[16] Ngwendson L, Deviny I, Coulbeck L, et al. Exploring the RBSOA boundaries of a 6.5kV/1000A trench gate IGBT module at different temperatures[C]//Inter- national Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Germany, 2020: 243-247.

[17] Schlapbach U, Rahimo M, Arx C, et al. 1200V IGBTs operating at 200℃? an investigation on the potentials and the design constraints[C]//Proceedings of Inter- national Symposium on Power Semiconductor Devices and IC's, Jeju, 2007: 9-12.

[18] Hu Ji, Alatise O, Gonzalez J, et al. Robustness and balancing of parallel-connected power device: SiC versus CoolMOS[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2092-2102.

[19] 彭程, 李学宝, 张冠柔, 等. 压接型IGBT芯片动态特性实验平台设计与实现[J]. 电工技术学报, 2021, 36(12): 2471-2481.

Peng Cheng, Li Xuebao, Zhang Guanrou, et al. Design and implementation of an experimental platform for dynamic characteristics of press-pack IGBT chip[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2471-2481.

[20] 丁强, 何湘宁. 采用Saber模型研究IGBT工作极限特性[J]. 电工技术学报, 2001, 16(2): 65-69, 60.

Ding Qiang, He Xiangning. Research on IGBT operation limits by using the model of Saber[J]. Transactions of China Electrotechnical Society, 2001, 16(2): 65-69, 60.

Steady Temperature Equalization Method for the Parallel IGBTs Considering the Thermal Resistance and the Matching Emitter Parasitic Inductance

11211

（1. State Key Laboratory of Alternate Electrical Power System With Renewable energy Sources North China Electric Power University Beijing 102206 China 2. State Key Laboratory of Advanced Power Transmission Technology Global Energy Interconnection Research Institute Co. Ltd Beijing 102209 China）

In the IGBT device with the parallel chips, the thermal resistance and emitter parasitic inductance are the key parameters which determine the steady junction temperature distribution. Therefore, to equalize the steady junction temperature of the parallel chips, it is vital to design the thermal resistance and emitter parasitic inductance reasonably. In this paper, an electrothermal model with two parallel IGBT chips is established to investigate the impacts of the junction temperature and the emitter parasitic inductance on the dynamic losses. Then, the effects of thermal resistance and emitter parasitic inductance on the temperature distribution are further studied by the electrothermal coupling simulation. On this basis, the steady temperature equalization method for the parallel IGBT chips is put forward. The proposed method can obtain the reference values of the thermal resistance or emitter parasitic inductance by solving the equation set rather than the complicated electrothermal calculation. Finally, taking two parallel IGBT chips as an example, the steady junction temperature of the parallel chips at different frequencies is demonstrated, which shows the effectiveness of the method.

Parallel IGBT chips, thermal resistance, emitter parasitic inductance, steady temperature equalization method

10.19595/j.cnki.1000-6753.tces.210751

TM46

国家自然科学基金委员会-国家电网公司智能电网联合基金资助项目（U1766219）。

2021-05-24

2021-07-20

范迦羽 男，1996年生，博士研究生，研究方向为高压电力电子器件封装。E-mail: fanjiayu@ncepu.edu.cn

李学宝 男，1988年生，博士，副教授，研究方向为高压大功率电力电子器件封装。E-mail: lxb08357@ncepu.edu.cn（通信作者）

（编辑 陈 诚）