故障扰动下振荡环型真随机数发生器安全特性及度量方法研究

罗 芳 欧庆于 周学广 褚潍禹 高 飞

(海军工程大学信息安全系 武汉 430033)

1 引言

作为现代密码系统中的基础核心要素，真随机数凭借其优良的统计特性和不可预测性，在各类密码算法、协议以及安全实现中发挥着举足轻重的作用。作为真随机数的物理生成实体，真随机数发生器(True Random Number Generator, TRNG)多基于现实世界中的不确定性过程(如：电子噪声、亚稳态现象等)进行设计，而这种与现实物理现象的交联可能会对密码应用的安全性造成威胁。例如，凭借电磁脉冲、电压毛刺等手段能够轻易穿透各类物理封装屏障，对TRNG实施扰动，造成熵源不可预测性退化，并最终达到使各类密码应用体系、防护体系的安全性降级的目的[1-4]。

为明确故障扰动场景下TRNG的安全特性，文献[5]对以TRNG为对象的故障注入及安全性扰动方法进行了研究，揭示了TRNG安全性与现实物理世界间的交联关系；在此基础上，文献[6,7]结合TRNG运行时的电磁发射特点，在时间维度上进一步提升了扰动的精确性及现实场景下的适用性，为开展以TRNG安全性验证为目的的攻击性测试奠定了良好基础。另一方面，为明确故障扰动下TRNG的安全变异特性，文献[8]对TRNG安全性形式化建模方法进行了研究，并结合TRNG关键影响参数，初步构建了TRNG安全性评估框架。然而，由于在故障扰动场景下，各TRNG关键参数受扰动概率传播、噪声分量突变等多重因素地影响，导致仅依托形式化建模的方法无法充分刻画TRNG遭受扰动时的行为特性，进而影响评估结果的准确性。针对这一问题，文献[9]以TRNG中的核心部件，如能带隙、锁相环等为对象，构建了电压毛刺影响下的行为模型，较好地解决了TRNG模数混合特性所带来的扰动传播分析问题，但对于扰动场景下噪声分量突变导致的安全性变异问题并未进行考虑，导致难以全面地揭示TRNG在故障扰动场景下的安全特性。此外，借助电磁脉冲故障注入手段，文献[10]对TRNG的熵减现象进行了研究；文献[11]对故障扰动下TRNG的自感应现象及其影响进行了分析。但上述研究对于电磁脉冲的安全扰动机理缺乏深入地探讨，使其无法满足TRNG安全特性表征的需求。

本文围绕故障扰动场景下TRNG的安全特性变异分析及度量问题，以当前广泛应用的振荡环(Ring Oscillator,RO)型TRNG为对象，从熵源和熵抽取两个方面，对由故障扰动造成的抖动方差累积影响及节拍延迟链时延突变现象进行了探讨，并对由此造成的安全性影响进行了深入分析；以此为基础，构建了以捕获偏置度为指标的TRNG安全性度量模型，实现了对由故障扰动引起的抖动方差累积非线性波动递增与时延突变等因素引起的安全性变异的综合表征。

2 RO-TRNG随机数生成原理

与基于亚稳态[12]、混沌[13]、电阻热燥声[14]等类型的TRNG相比，RO-TRNG利用源于热噪声的信号边沿抖动随机性实现随机数的生成，具有结构简单、吞吐率高、便于数字化实现等优点，在可编程逻辑门阵列(Field Programmable Gate Array,FPGA)、片上系统(System On Chip, SOC)、可编程片上系统(System On a Programmable Chip, SOPC)等各类数字电路芯片中得到广泛应用。

3 故障扰动对RO-TRNG特性的影响

基于式(3)可知，RO-TRNG的不可预测性仅假设源于热噪声的振荡信号抖动。然而，现实中振荡信号会受到闪烁噪声等内源性噪声分量影响，还可能遭受电磁干扰、电压毛刺等形式的故障扰动影响。

3.1 故障扰动对熵源特性影响

3.2 故障扰动对熵抽取特性影响

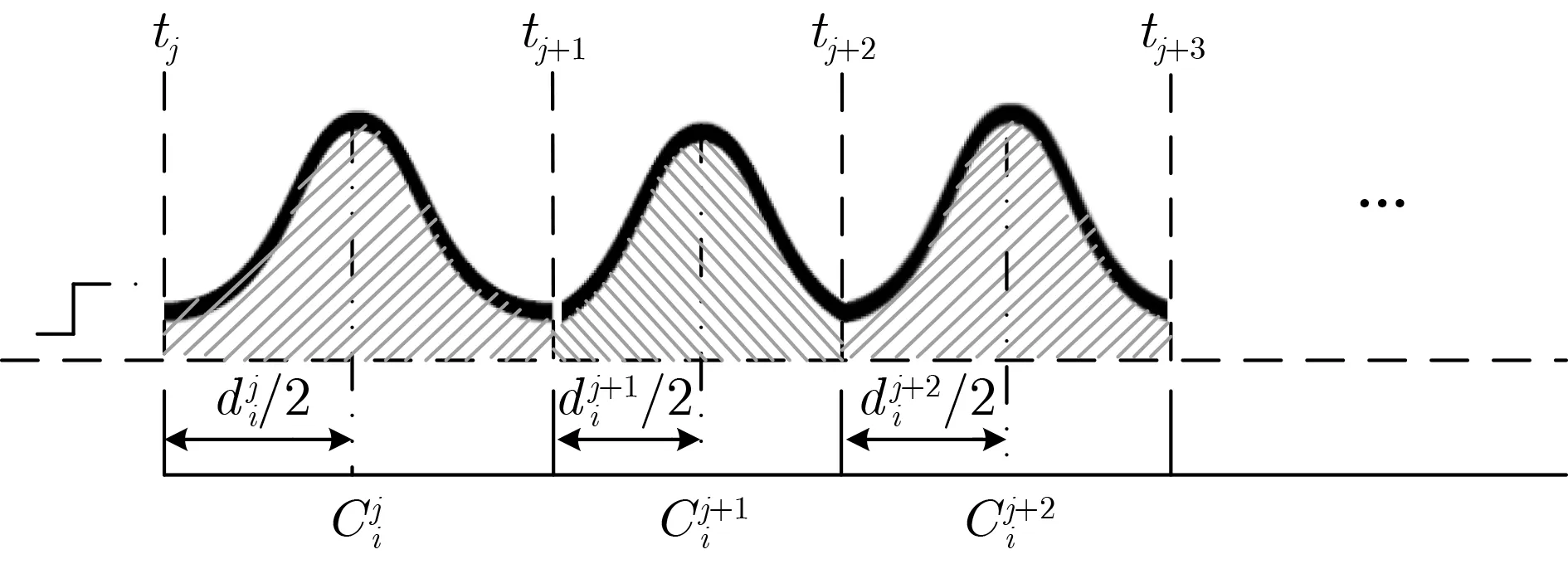
图1 TDC的非均匀特性

4 故障扰动场景下RO-TRNG安全性度量方法研究

4.1 故障扰动场景下RO-TRNG安全性分析

4.2 故障扰动场景下RO-TRNG安全性度量

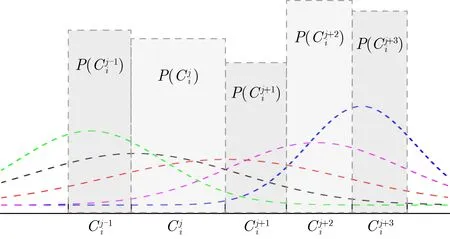
图2 故障扰动下的捕获概率偏置

5 测试及分析

5.1 测试环境

测试环境包括：基于Xilinx XC6SLX45实现的RO-TRNG, Time-Waves 6000A型故障注入器、函数信号发生器、示波器等。基于函数信号发生器生成的周期触发信号(周期100 ns)，连续驱动故障注入器产生电压脉冲，实现对FPGA核心电源系统的电压毛刺故障注入，最终在FPGA核心电源系统中形成幅度为+5.7～-3.1 V的电压毛刺，上升沿为862.1 ps(10%～90%)，下降沿为1.1679 ns(10%～90%)，如图3所示。RO-TRNG实现如图4所示。其中，采样时钟频率为100 MHz，振荡环由3级延迟单元构成，3级节拍延迟链基于XC6SLX45中的Carry4快速进位链逻辑实现，每级为40 bit。

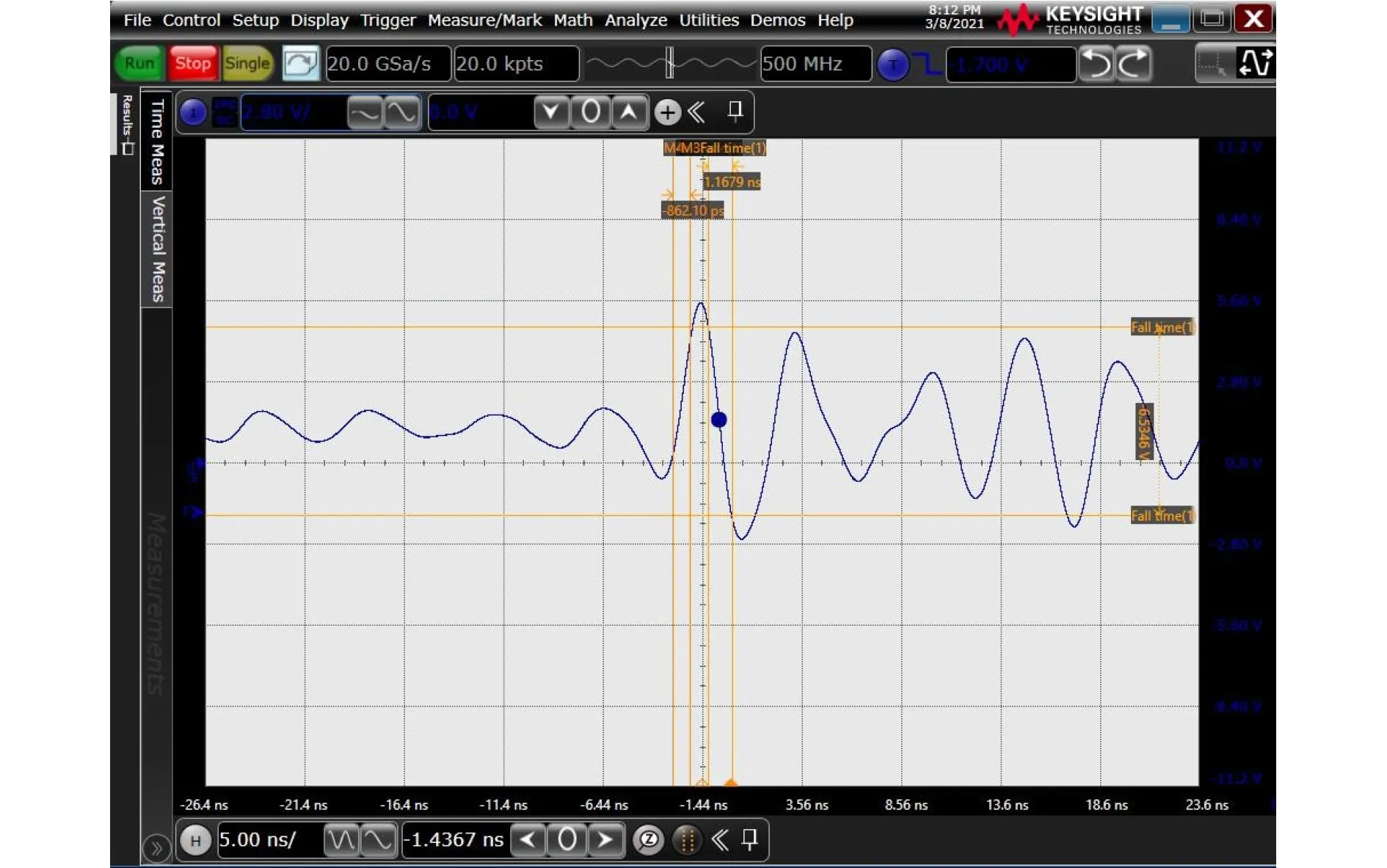
图3 FPGA核心电压毛刺注入

图4 RO-TRNG实现布局

5.2 故障扰动对方差累积影响的测试分析

基于文献[22]的方法，通过507376次采样测得振荡环平均周期T0为3.2863 ns，并分别在累积时间tN为800 ns, 1600 ns, 2400 ns, 4000 ns, 5000 ns,10000 ns时，对正常和故障扰动场景下的累积方差进行测量，结果如表2。

表1 不同序号捕获概率变化趋势

表2 方差累积特性测量结果

如图5所示，通过对正常情况下累积方差σN2进行拟合可知，振荡环熵源的方差累积基本符合线性增长规律。在同样的累积时间下，当存在故障扰动时其累积方差值显著大于正常情况下的累积方差，说明通过故障扰动，熵源中闪烁噪声分量已处于支配地位；累积时间为2400 ns和4000 ns时，故障扰动下的累积方差存在较大波动，说明除受闪烁噪声分量影响外，累积方差还受到故障扰动的全局性影响。

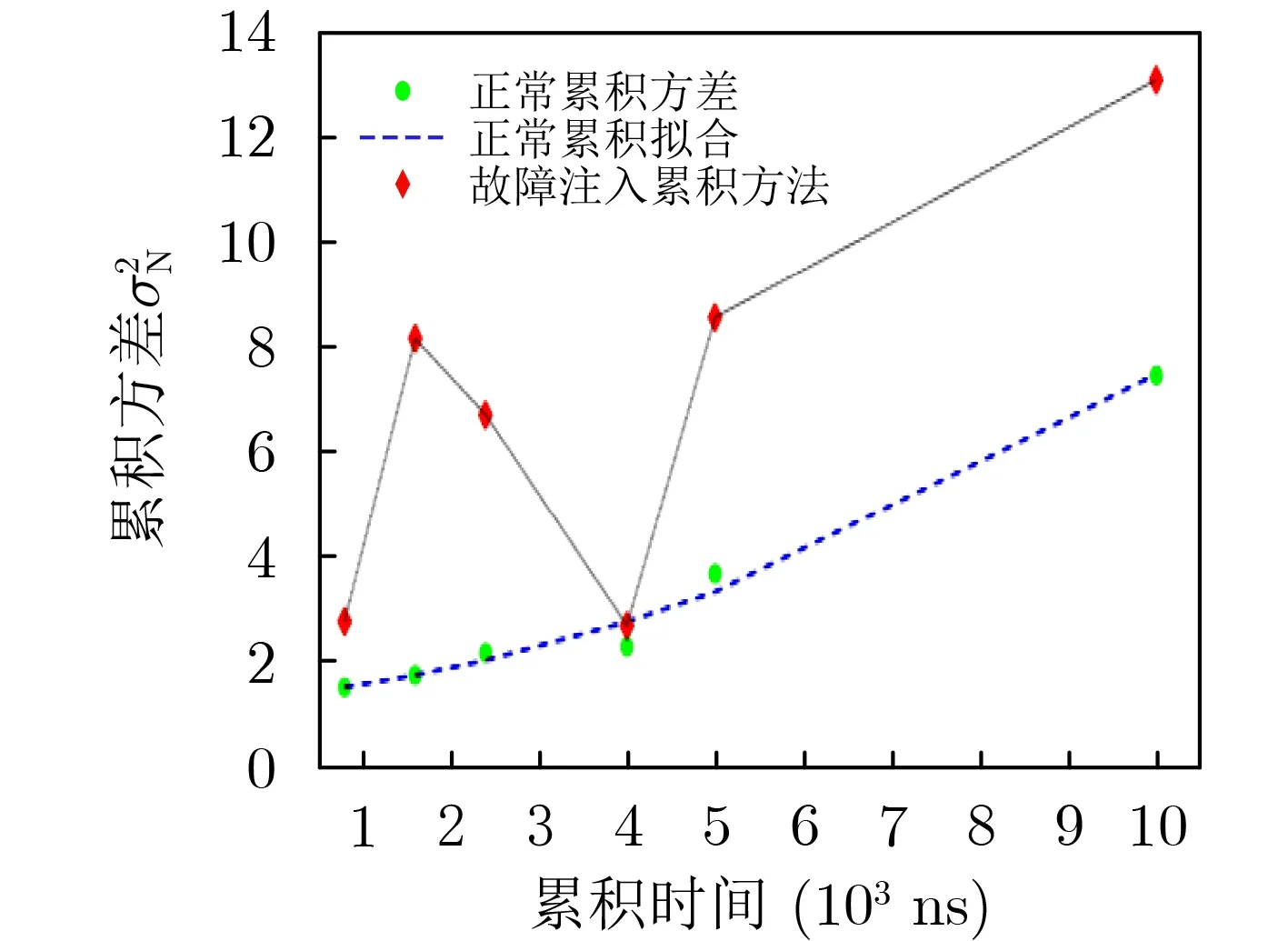
图5 方差累积特性的对比

5.3 基于捕获偏置度的安全性度量

基于蒙特卡洛方法[22]，在振荡环连续振荡下，分别对正常情况和故障注入情况时，TDC各延迟单元的时延进行测量，结果如图6所示。

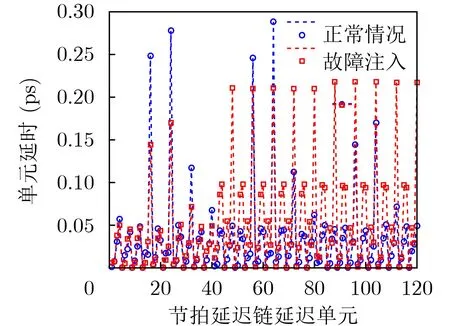
图6 节拍延迟链时延变化特性测量结果

通过对测量结果进行分析可知，在故障注入情况下，节拍延迟链中各延迟单元的时延产生了较大波动，且随着时延波动在节拍延迟中累积，在第40个延迟单元后，故障注入情况下的时延显著大于正常情况下的时延。为确保具备足够的方差累积，在累积时间设定为1600 ns时，对TDC中各延迟单元对振荡信号上升沿的捕获概率进行测量和估计，其结果如图7所示。

图7 振荡信号捕获概率变化特性测量结果

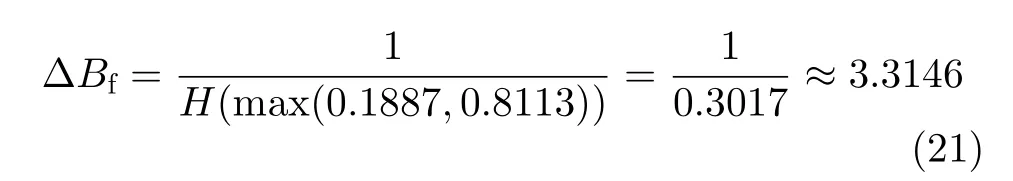
显然，在故障扰动下，其上升沿捕获偏置显著大于正常情况，从而将造成输出随机数的偏置。

与当前TRNG领域广泛采用的频率度量、Maurer通用统计度量方法进行比较，如表3所示。其中，频率度量和Maurer度量所使用的随机数序列基于TDC振荡信号上升沿被奇偶序号延迟单元捕获情况直接转换。通过比较可知，由于基于熵源直接产生的原始随机数未经过后处理部分的再处理，其随机性无法达到相关标准的要求，导致频率度量和Maurer度量结果均无法超过阈值。此外，当度量结果小于阈值时，受度量方法及样本数量的限制，其正常场景度量和扰动场景度量结果的差异程度较小。其中，采样次数为10000时，频率度量和Maurer度量均无法对输出序列随机性进行准确度量；采样次数为200000时，频率度量针对两种场景度量结果的差异程度为0.00113，而Maurer度量无法正确区分正常场景和扰动场景；采样次数为5000000时，频率度量的差异程度为0.00274，Maurer度量的差异程度为0.00058。另一方面，基于捕获偏置度的度量方法虽然在采样次数为10000时，同样无法实施准确度量，但当采样次数上升至200000时，正常场景和扰动场景度量结果的差异程度达到了0.6014。这意味着当样本数量较小时，基于捕获偏置度量的方法能够更快速地监测熵源扰动造成的安全特性变化，且其灵敏度高于频率度量及Maurer度量，适用于对故障扰动场景下TRNG的安全性实施快速客观评价。

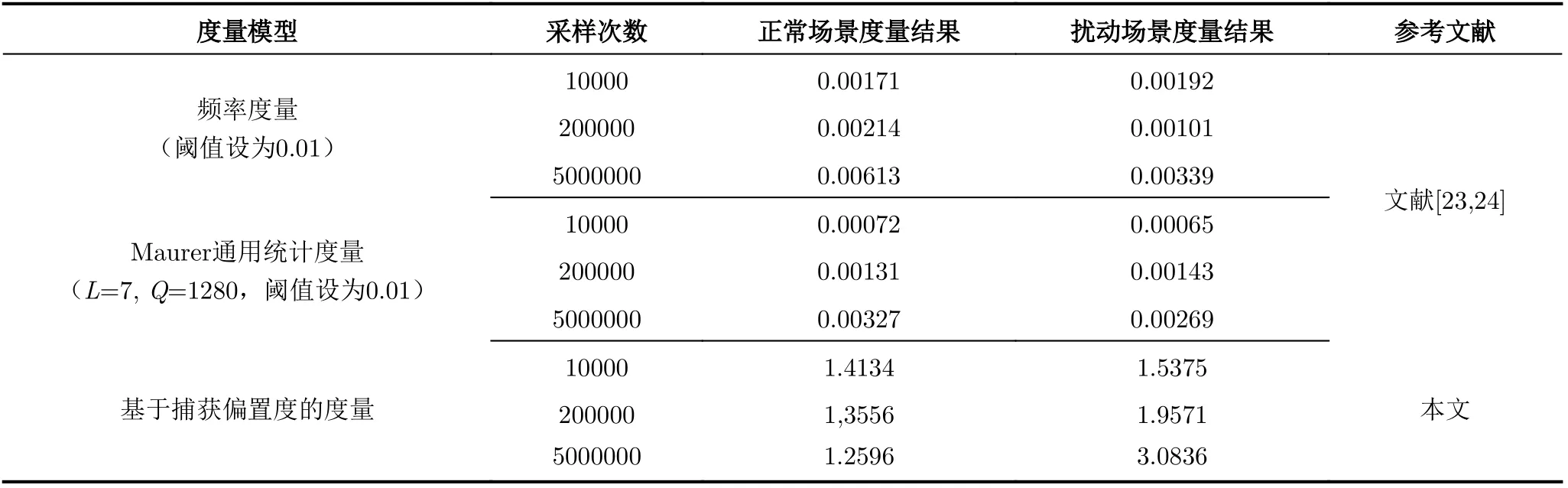
表3 与其他度量方法的对比

6 结论

围绕RO-TRNG在故障扰动场景下的安全特性分析和度量问题，本文在对故障扰动施加于熵源和熵抽取部分的影响进行深入分析的基础上，以抖动方差累积和节拍延迟链时延为核心要素，对故障扰动场景下RO-TRNG的安全特性和度量方法进行了研究，并以此为基础提出了能够充分反映故障扰动场景下RO-TRNG安全特性的度量模型。该度量模型能够充分反映故障扰动场景下，抖动方差累积非线性波动递增与时延突变特性，以及由此引起的安全性变异，从而为基于振荡环方式实现的真随机数发生器的抗故障攻击能力的客观评价提供依据，并可为抗故障攻击能力的改进提供参考，对于增强密码应用的现实安全性具有重要意义。