三维燃烧火焰辐射成像模型及其构建算法
2022-06-25黄志锋
张 杰,程 勇,黄志锋
三维燃烧火焰辐射成像模型及其构建算法
张 杰,程 勇,黄志锋
(武汉大学动力与机械学院,武汉 430072)
基于辐射图像的燃烧温度场测量方法由于其系统简单、对被测对象无干扰等特点而受到广泛关注.该测量方法中建立准确的辐射成像模型以获得三维燃烧火焰发射和二维辐射图像间对应关系是温度场准确测量的前提.基于点扩散函数的透镜成像模型能够考虑三维燃烧火焰中聚焦平面内外发射点的不同成像特性,适用于不同的燃烧对象和辐射成像系统.针对现有成像模型构建算法在计算精度或计算时间上存在的不足,通过分析发射点在成像面上的能量分布函数,得到改进的辐射成像模型构建算法.以简化的三维燃烧火焰为研究对象,利用不同算法获得辐射图像并进行对比分析.结果表明,文中改进的辐射成像算法具有很好的计算精度,且计算效率高于蒙特卡罗方法.
三维燃烧火焰;辐射图像;辐射成像模型;点扩散函数
燃烧现象普遍存在于火力发电等能源领域和航空航天、交通运输等动力工程领域.对燃烧的全面了解有助于更好地对其进行组织进而提高燃烧效率和降低污染物生成,这在当今能源短缺和环保要求越来越高的形势下显得尤为重要.燃烧温度作为体现化学反应速率的重要参量,不仅对验证化学反应动力学模型、揭示燃烧规律具有重要的意义,而且对监测燃烧装置(如电站锅炉、工业炉等)的运行状态、提高其运行安全性和经济性具有重要的作用[1].辐射成像技术作为一种被动式的光学测温方法,具有对被测对象无干扰、响应速度快等特点,同时能够获得大量像素所对应方向上的高温介质的投影信息,便于燃烧空间的三维温度场测量,因此倍受关注[2-7].
利用辐射成像技术进行三维温度场测量,需要建立准确的燃烧火焰三维能量发射和二维辐射图像间对应关系,即辐射成像模型.现有基于辐射成像技术的燃烧三维温度测量工作主要应用小孔成像模型[2-5]和透镜成像模型[6-7].小孔成像模型中物像间成线性关系,关于小孔呈中心对称,是一种理想的成像模型.当物体位于聚焦平面上时,小孔成像模型与透镜成像模型建立的物像间对应关系相同.然而,对于实际燃烧火焰等三维物体,位于聚焦面之外的发射区域在成像面上会发生离焦而产生模糊现象.此时,利用小孔成像模型建立的物像间对应关系将会产生不同程度的误差.
Floyd等[8-9]通过透镜成像模型建立了三维燃烧火焰和二维辐射图像间映射关系,并考虑了由于探测器景深小于被测物体时的模糊效应.Cai等[10]和Li等[11]通过引入点扩散函数来描述火焰中不同发射点在成像面不同像素上的权重矩阵.利用蒙特卡洛方法模拟各物点发射的能量在成像面各像素上的分布特征,以获得点扩散函数,从而建立辐射成像模型.该方法需要发射大量的能束,计算时间较长.为了提高计算效率,Wang等[12]基于透镜成像理论,获得不同发射物点对成像面各像素的权重矩阵,建立了三维燃烧火焰和二维辐射图像间映射关系.通过假设点光源发射所形成的光斑内能量分布均匀,且利用近似方法计算落在各像素中的能量比例,大大提高了计算效率,然而却由于引入近似处理使得辐射成像模型存在误差.
为了在较短计算时间内获得高精度的辐射成像模型,本文将理论分析和数值计算相结合以计算发射空间的点扩散函数,通过获得的点扩散函数构建高精度的三维燃烧火焰辐射成像模型.文中首先对现有文献中(Cai等[10]和Wang等[12])所采用的两种辐射成像模型构建方法进行简要介绍.接着介绍本文中所采用的辐射成像模型构建方法,并对比不同算法的计算效率和精度.然后,以简化的三维燃烧火焰模型为分析对象,讨论不同方法对辐射成像结果的影响. 最后,对全文进行总结.
1 辐射成像模型及现有构建算法介绍
1.1 辐射成型模型
物体发出的辐射能量,只有其中的一部分通过镜头被探测器捕获,继而在探测器中通过信号处理将光信号转换为电信号而产生图像.在这一过程中,获得准确的物与像之间的对应关系是建立辐射成像模型的关键.本文的辐射成像模型研究基于以下两点假设:①辐射物点在空间各方向的发射具有各向同性的特点;②不考虑物点辐射能量沿传播路径发生的吸收、散射等衰减.这两点假设对于实验室小型气体燃烧火焰通常是合理的.
基于上述假设,将待测区离散为连续的空间网格,各网格发射能量视为网格中心点位置处集中发射,最终得到的辐射图像为各离散网格点在成像平面内所成像的叠加.物像之间对应的辐射成像模型如图1所示.
图中给出了聚焦平面、镜头平面、成像平面与待测区的位置关系.由于透镜成像模型对光线的汇聚特点,聚焦面上的物点在成像面上形成的圆斑半径最小而接近于点,聚焦面以外各平面内的物点将在成像平面上形成具有一定半径的扩散圆斑.扩散的圆形光斑的位置和大小与辐射物点与探测器的相对位置、探测器的通光孔径相关.
1.2 现有辐射成像模型构建算法
基于点扩散函数的辐射成像模型,各物点辐射能量与辐射图像之间关系表示为[10-11],
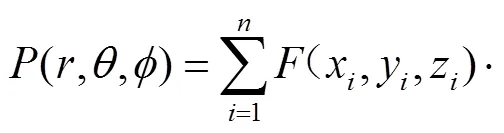
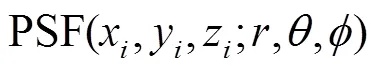
式中:(,,)表示探测器在全局坐标系中的位置和角度;表示探测器获得的二维辐射图像;(x,y,z)表示对应于第个网格的空间坐标;(x,y,z)表示位于(x,y,z)处物点的发射辐射;PSF(point spread function)表示成像系统的点扩散函数.对于待测区内的物点,利用正向蒙特卡罗方法,从每个物点处发射大量能束,并跟踪能束落在探测器像面上的位置,统计每个像素上捕获的能束数,计算出每个像素获得的辐射能量,从而得出每个物点对于像面的点扩散函数PSF,进而建立物像间对应关系.在实际的辐射成像模型中,由物点发射的辐射能量只有少部分通过探测器镜头到达像面,仅这部分辐射能量对于成像具有贡献.可通过定向发射能束,缩小角度范围到能够到达探测器镜头区域对应的角度以提高计算效率.本文中后续所使用的蒙特卡罗法均为上述的定向蒙特卡罗法[13].
以上工作是通过点扩散函数来表示不同发射物点对成像面上不同像素的能量贡献,进而获得辐射成像模型.类似地,Wang等[12]通过权重矩阵来描述不同发射物点对不同像素的能量贡献而建立辐射成像模型.在该辐射成像算法中,将辐射物点对成像面上像素的贡献强度表示为[12]
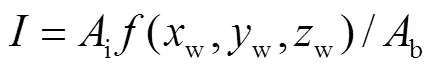
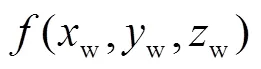
如图2所示,对于不同的圆形光斑大小以及光斑和像素不同的相对位置,辐射物点能量在像面上的分配计算公式存在差异.当圆形光斑面积大于或小于像素面积时,i/b分别由式(3)和(4)给出[12]:
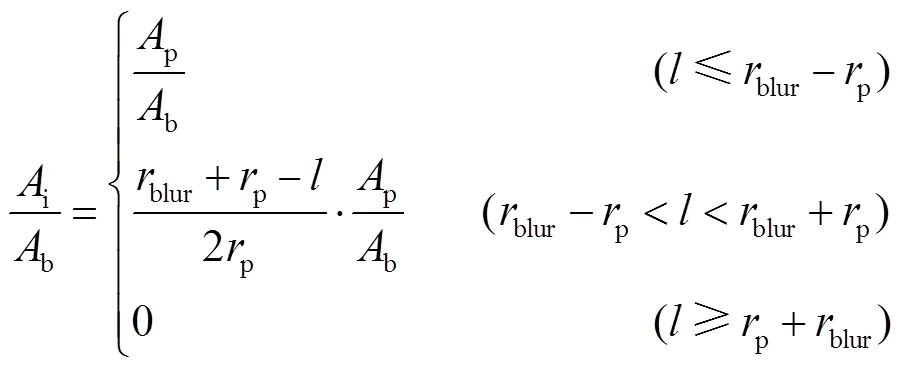
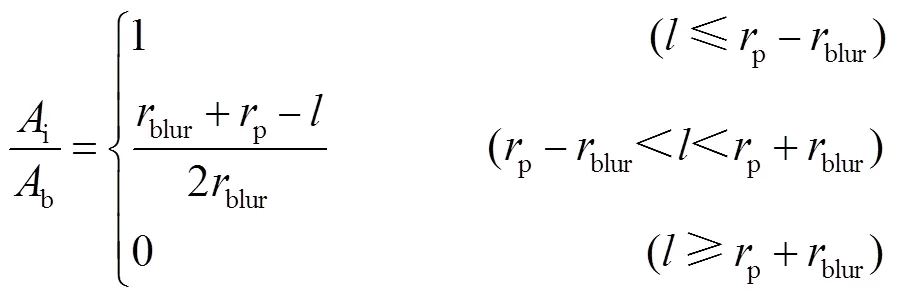
式中:p为像素面积;blur为圆斑半径;p为像素边长的一半;表示圆形光斑圆心与像素中心间距离.该方法将每个物点形成的圆形光斑内能量视为均匀分布,通过对圆形光斑的面积进行分割,近似得出每个像素获得的光斑能量份额.
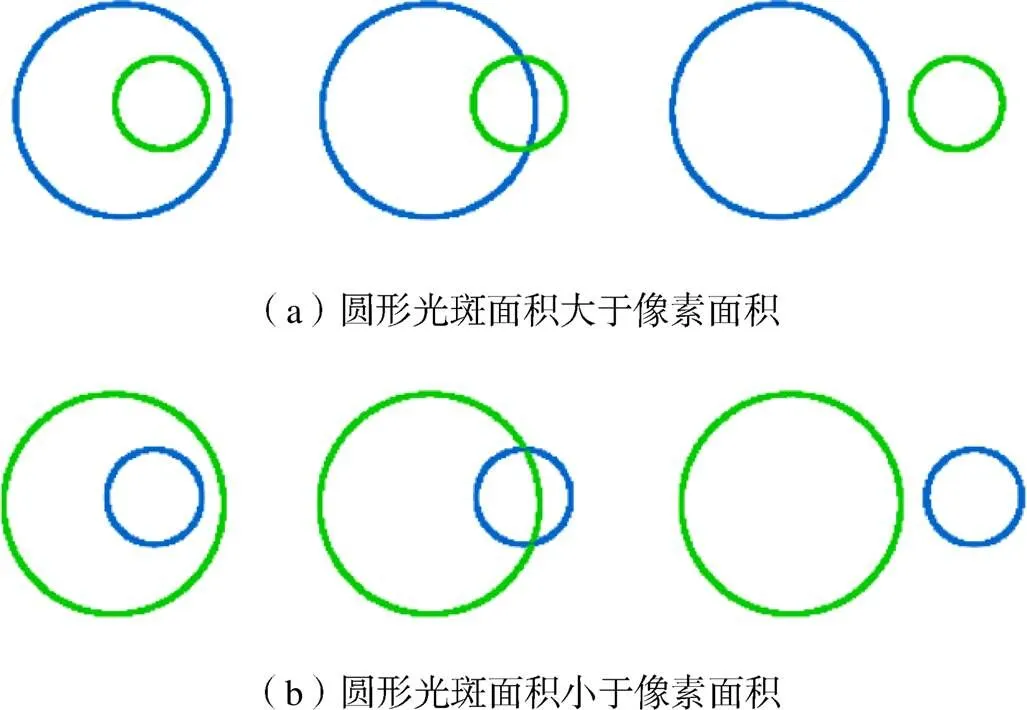
图2 圆形光斑(蓝色)与像素(绿色)位置关系[12]
2 改进的辐射成像模型构建算法
根据以上介绍,Cai等[10]和Li等[11]基于蒙特卡罗法的辐射成像算法通过发射大量的能束可获得较好的计算精度,然而由于计算时间长,无法满足一些需要实时计算的应用场合.Wang等[12]在构建辐射成像算法时采用了近似处理,计算效率大为提高,但计算精度受到影响.本文利用几何光学成像理论,通过分析物与像之间的能量对应关系,获得三维火焰中不同发射点在成像面上的能量分布函数.并利用该分布函数的特点,获得发射点辐射能量在不同像素内的分布,即各发射点的点扩散函数.利用建立的点扩散函数获得准确的物像对应关系,构建辐射成像算法.文中将该方法称为分布函数法,以下将具体进行介绍.
2.1 物点的有效辐射能量份额
当物与镜头的相对位置不同时,不同发射物点到达成像平面的辐射能量份额是不同的,这个差异大小与被测物体大小和探测器参数相关.离散后的发射物点通过镜头到达像面上的辐射能量份额,主要取决于镜头的通光孔径占发射物点的三维空间角度.即一个发射物点发射的诸多能束中,只有其中一部分能够通过探测器镜头落在成像平面上.针对上述辐射成像模型,建立解析的方法,将处于待测区任意位置处的一个物点,通过建立几何空间关系,计算透过镜头的有效辐射能量份额.
将上述的发射物点与镜头的相对位置关系表示为图3.将镜头所在的平面作为平面,以物点为顶点对镜头进行微分,得到探测器镜头的空间角度,从而获得探测器捕获的有效辐射能量份额,物点的有效发射能量通过镜头积分得到.
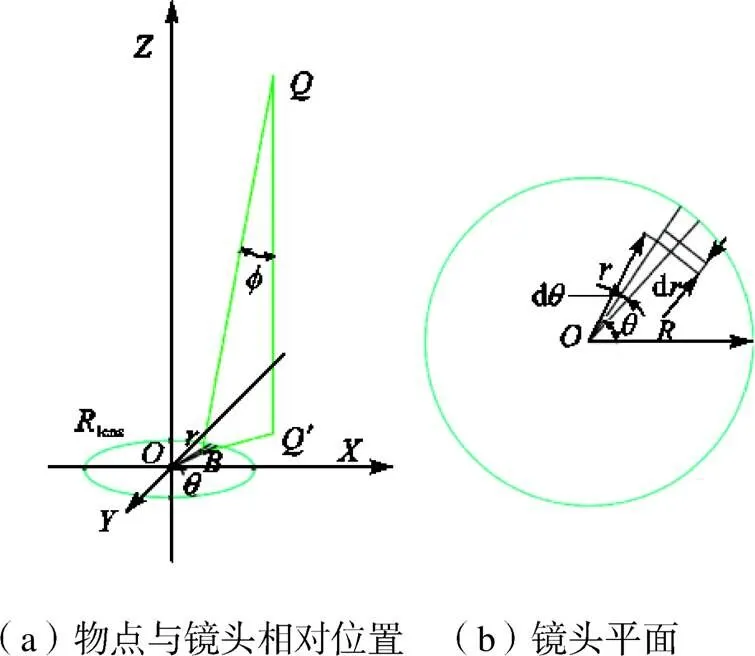
图3 辐射物点与镜头相对位置

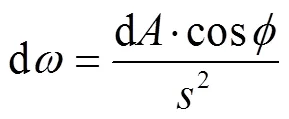
将式(6)带入式(5)可得:

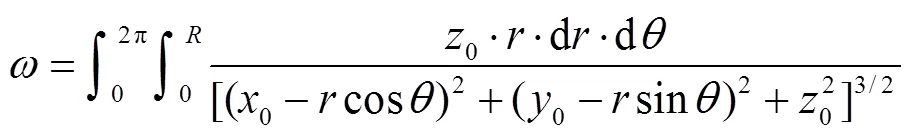
由上述公式可知,当空间物点与探测器的相对位置确定以后,某物点发出的能够通过镜头到达像面的辐射能量可以依照上式算出,并且对该部分的求解完全取决于探测器与待测区之间的相对位置,与待测区的发射特性无关.
2.2 成像圆斑内辐射能量分布
能量密度为成像平面内单位面积接收到的辐射能量.待测区经过离散后,不同位置处的辐射物点与镜头的相对位置都不相同,故物点在成像平面上形成的圆斑内辐射能量也具有不同的能量密度分布.
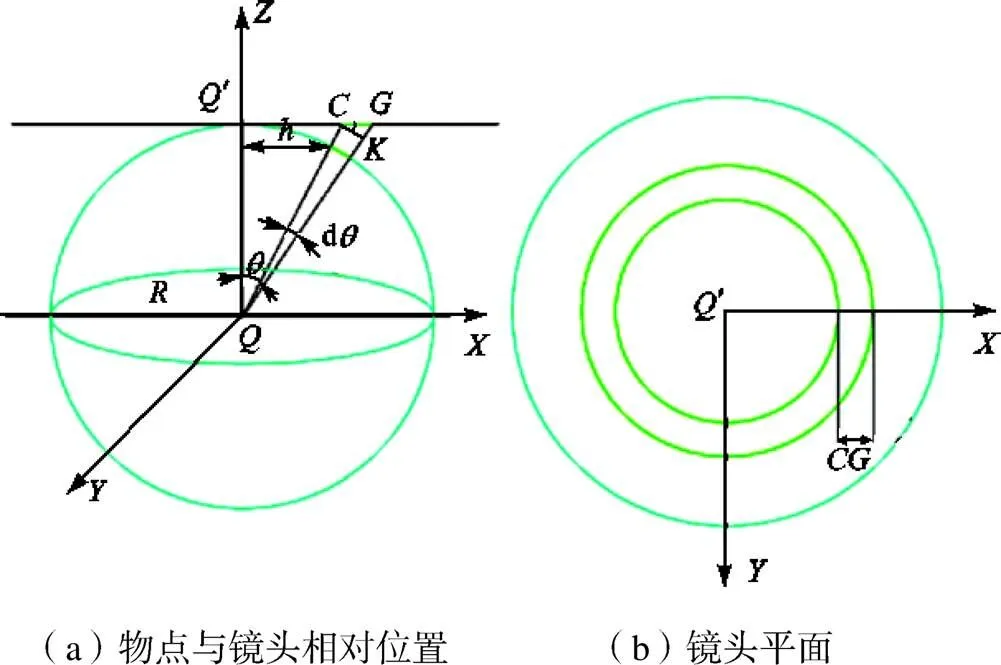
图4 辐射物点能量密度分布
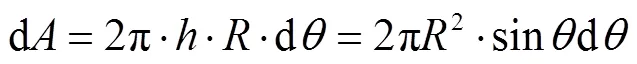
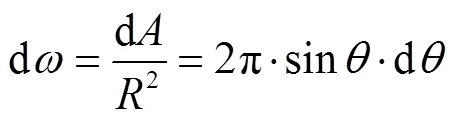
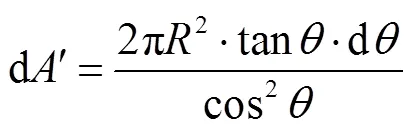
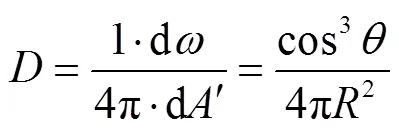
由式(12)可知,物点向空间各方向均匀地发射能量,其在平面上形成的能量密度并不均匀.当物点与镜头的相对距离保持不变时,物点投射在平面上的辐射能量密度随着角度的增大呈现减小的趋势.
2.3 分布函数法计算辐射成像
以上获得了三维燃烧火焰不同发射点辐射能量在二维成像面内的分布函数.为了获得点扩散函数,需要对到达像面上辐射能量进行逐像素分配.本文中按照辐射能量的分布特点在圆斑内产生一定数量的点,并统计各像素内点的着陆情况,从而得出各个像素内获得的辐射能量份额.
分布函数法和蒙特卡罗法的主要不同在于,前者利用成像圆斑内能量分布模拟辐射能量在不同像素内的分布情况,而后者是通过大量发射能束来获得不同像素内的能量分布情况,以下将以具体算例来进行说明.图5给出了物点不在探测器成像光轴上时镜头与物点形成的张角的角度范围示意图.当物点与镜头的相对位置不同时,发射能束的角度范围不同.
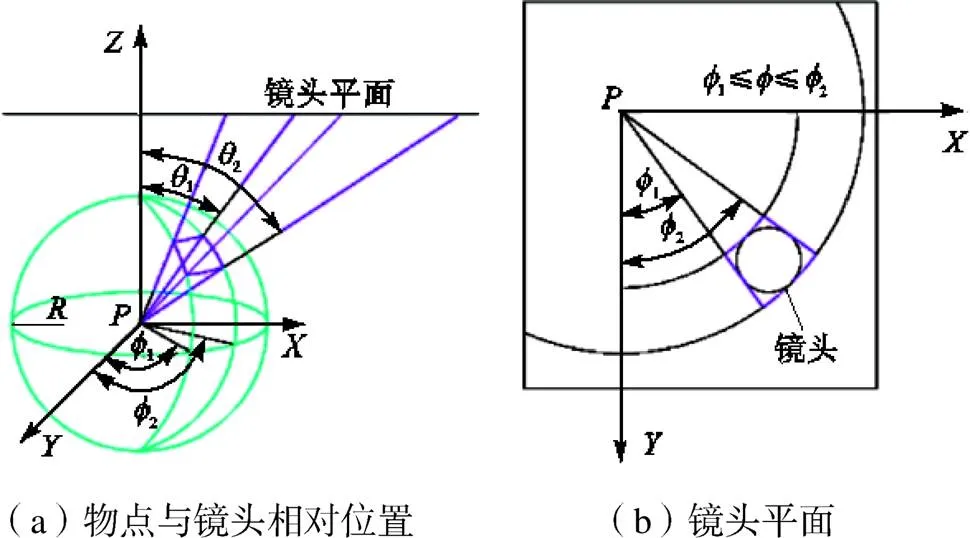
图5 镜头对物点的有效空间角度范围
在物点的有效发射范围内,分别利用蒙特卡罗法和分布函数方法获得成像圆斑内的辐射能量分布.模拟发射的发射能束数越多,辐射算法的计算时间越长.如何在物点发射能束数较少的条件下,准确计算出物点的辐射能量在成像平面上的分配尤为重要.
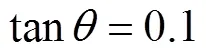
图6 不同方法能束落点分布()
总结本文中分布函数法获得辐射成像模型的具体步骤为:
(1) 根据发射物点与镜头的相对位置,计算出能束能够通过镜头到达像面上的角度范围,进而得出该物点的有效辐射能量份额;
当天中午,警方在发现线索后对关小美的宿舍进行搜查,在床下找到了作案工具水果刀。警方立即将目标锁定在郭启明身上, 随即对他和关小美进行通缉。 第二天中午12点,两人被警方抓获。
(2) 计算物点在像面上成像的位置与大小,获得成像圆斑内的能量分布函数;
(3) 在成像圆斑内按分布函数产生离散点,并统计各像素内辐射能量分布,获得点扩散函数;
(4) 叠加三维火焰的所有发射点的能量分布获得二维辐射图像.
3 不同辐射成像模型构建算法比较
3.1 计算模型介绍
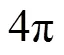
选取某实际探测器和镜头的参数进行模拟计算.主要参数包括:镜头焦距为8mm,探测器镜头直径与焦距比为1∶1.4,全开光圈.选取成像面的尺寸大小为120×60像素,像元尺寸为0.08mm×0.08mm.
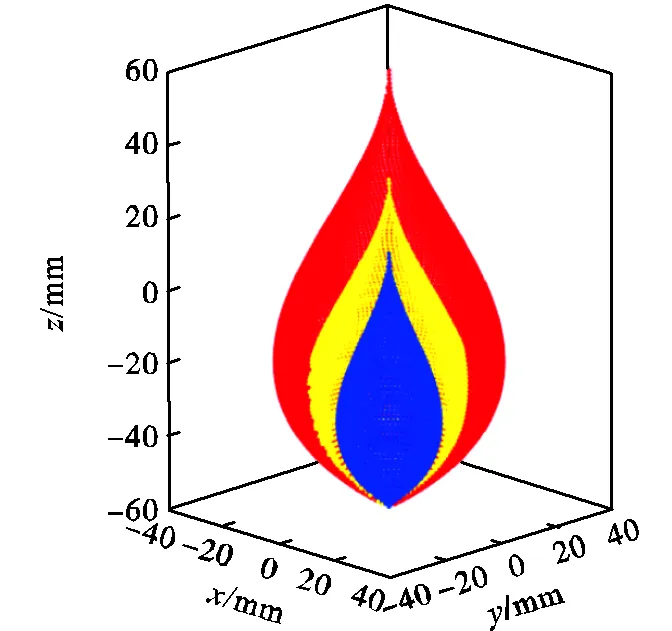
图7 蜡烛火焰简化模型
为了对比不同辐射成像模型构建算法的精度和计算效率,接下来首先讨论对单个发射物点的辐射所形成的圆斑能量分配结果,接着讨论分析所有物点所成像的叠加而成的二维辐射图像结果.
3.2 单点辐射能量分配准确性对比
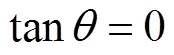
为了定量对比分布函数法与蒙特卡罗法计算得到的某一发射物点到达像面上的辐射能量在各像素的分布,以像斑覆盖像素数等于4为例,考虑不同的像斑位置与大小,以蒙特卡罗法发射大量能束下(108数量级)的收敛结果为基准,对不同方法计算得到的一个发射物点的成像误差进行对比.图10为两种方法在发射能束数相同时的平均误差结果.从图中可见,各算法在发射能束数增加时,计算误差随之减小,计算准确性得到提高.发射能束数相同时,分布函数方法的计算误差低于蒙特卡罗方法.
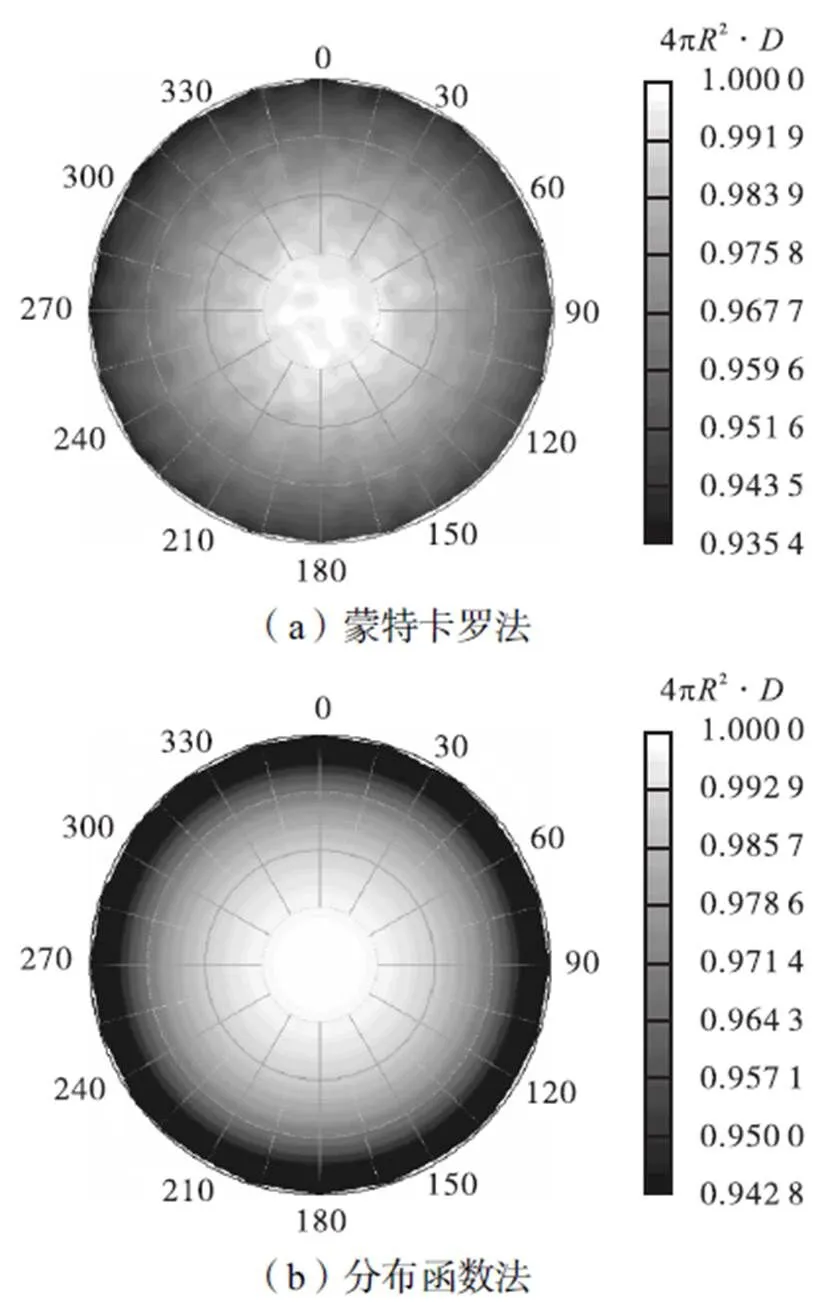
图8 物点辐射能量分布()
图9 物点辐射能量分布()
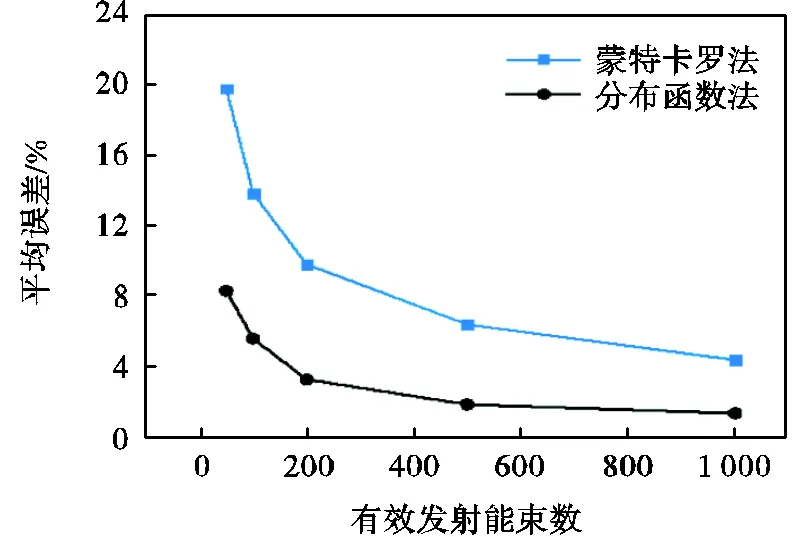
图10 不同能束数下辐射能量分布平均误差
3.3 辐射成像结果对比
以下分析不同算法得到的二维辐射图像结果. 对于分布函数和和蒙特卡罗法,随着物点发射的能束数增加,误差逐渐减小.计算结果表明,对于蒙特卡罗法,当每个物点发射大于1000条有效能束时,随着有效能束进一步增加,辐射图像结果保持不变.因此,以该收敛的辐射图像作蜡烛火焰二维辐射图像的基准值,如图11所示.相同条件下不同成像算法计算得到的辐射能量与之比较,相对误差计算式为
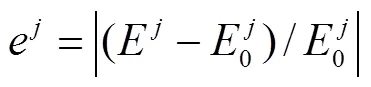
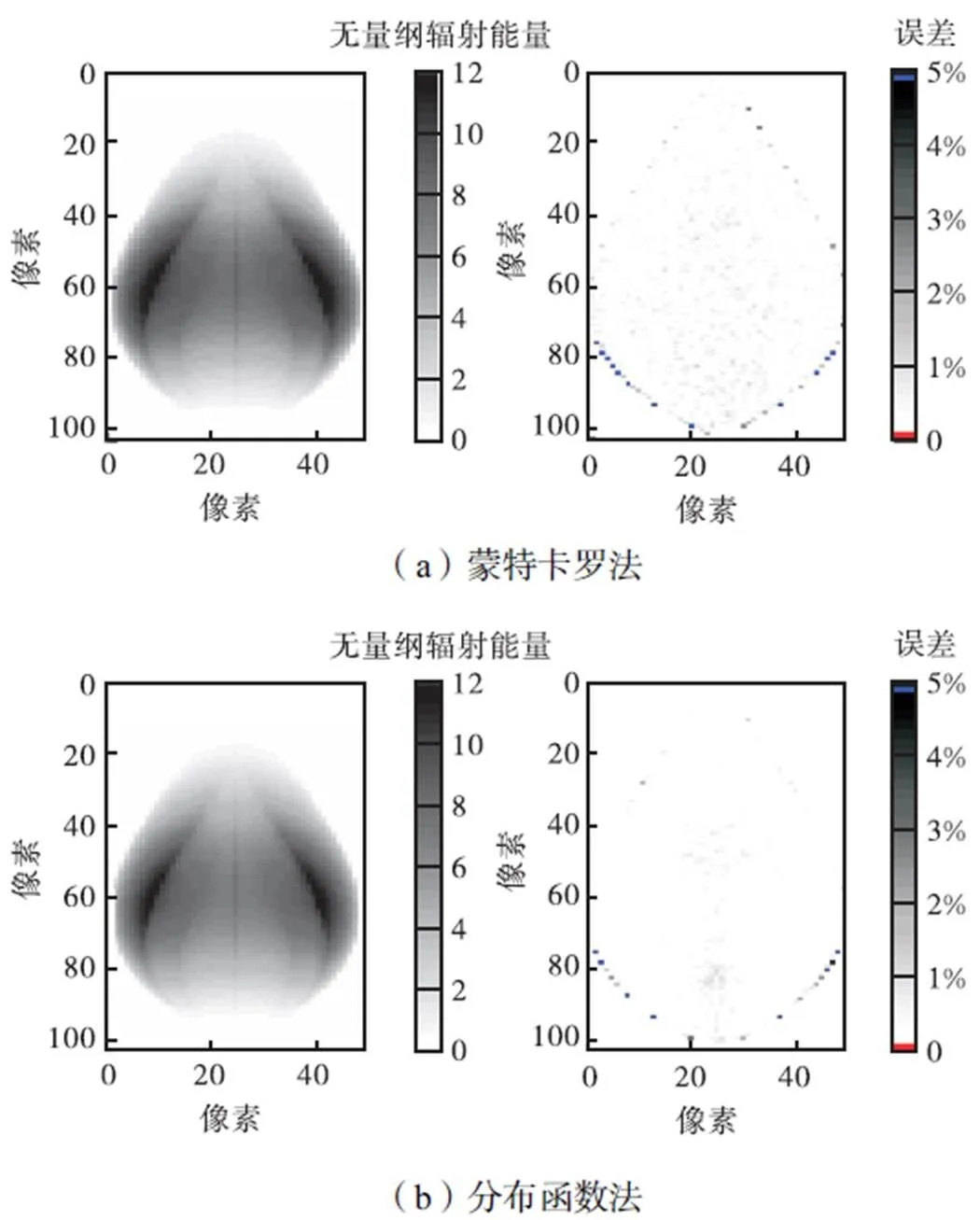
图12给出了3种不同的辐射成像模型构建算法计算得到的二维辐射图像结果和误差图.文献[12]方法不需要发射能束,对蒙特卡罗法和分布函数法,有效发射能束数为50.从图中看出,文献[12]方法各像素的误差较大,大部分误差在20%左右.在相同的能束数条件下,分布函数法比蒙特卡罗法有更好的精度,这与图10得到的结论一致.另外,各算法在成像边缘处的误差相对于其他位置处偏大,辐射能量叠加多的成像区域相对误差较小.
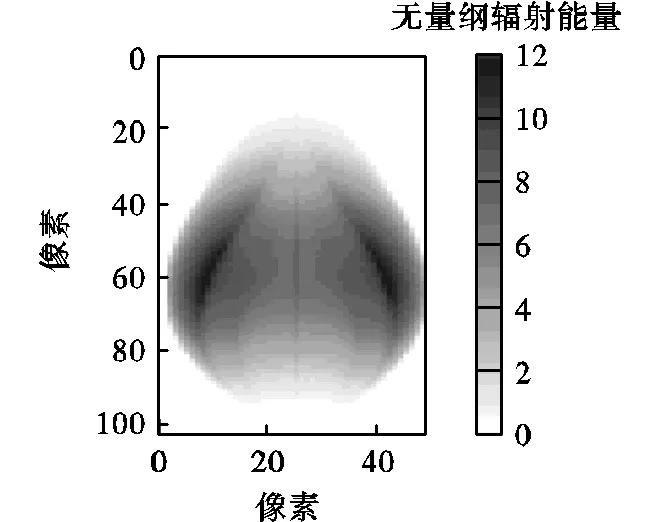
图11 蜡烛火焰辐射图像
由前面分析可知,随着各物点发射能束数的增加,辐射成像算法的计算精度随之提高,但计算时间随之增加.表1给出了在不同的能束数条件下,不同算法的计算精度和计算时间.用于计算的个人计算机CPU为Intel Core(TM)i5-7500CPU,主频为3.40GHz,内存为8.0G,所使用的编程软件为MATLAB R2017a.
表1 不同辐射成像算法特性对比
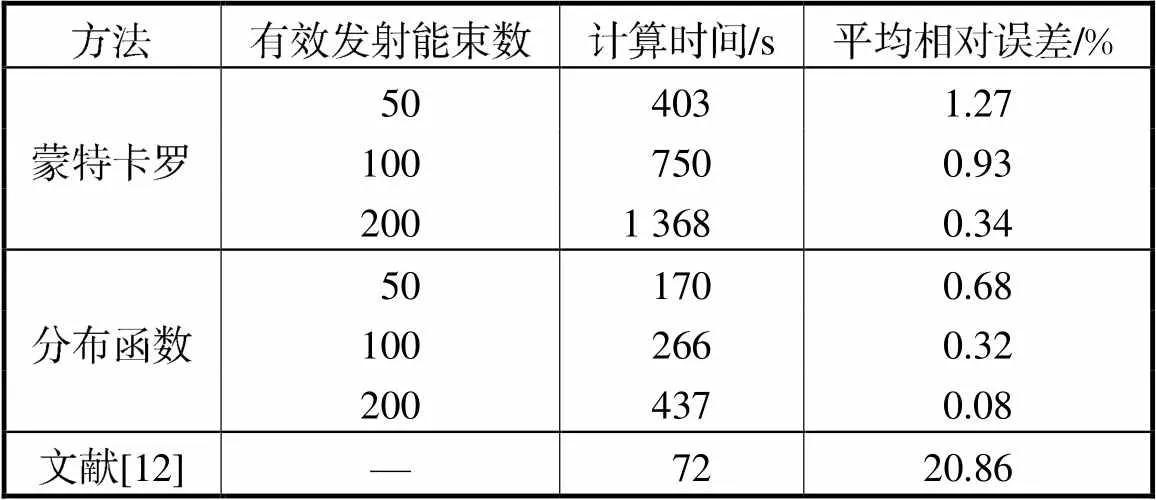
Tab.1 Comparison of performance among different cal-culating methods for radiative image
由表1中各算法的计算结果可以看出,蒙特卡罗法与分布函数法在计算准确性上明显优于文献[12]中的几何近似方法.在相同有效发射能束数50时,分布函数法具有的计算准确性又高于蒙特卡罗方法.蒙特卡罗法最大误差在14%,平均误差为1.27%;分布函数法的最大误差为9%,平均误差为0.68%.几何近似[12]的方法由于不需要产生发射能束,只需计算发射点在成像平面内的成像位置以及大小,在待测区网格划分确定以及成像平面内的像素数确定时,计算结果便与物距一一对应地确定下来.该方法计算时间最短,但由于对成像的过程存在简化处理,最终成像结果具有的误差较大,平均误差约为20.86%.
总体上,文献[12]中近似方法计算时间短,但计算误差较大;蒙特卡罗法在有效发射能束数达到一定数量时,具有很好的计算准确性,但计算成本较高;相对于蒙特卡罗法,本文中采用的分布函数法以较短的计算时间获得较高的计算精度,具有一定的优势.
4 结 语
准确的辐射成像模型是建立三维燃烧火焰发射和二维辐射图像间对应关系的基础,对基于辐射图像法的三维温度场重建技术具有重要作用.本文针对三维燃烧火焰不同发射物点对成像面内各像素辐射强度的不同贡献权重,以透镜成像原理为基础,分析得到各发射物点在成像面内的能量分布函数,进而得出各发射物点的点扩散函数并建立辐射成像模型.
文中以发射大量能束而得到收敛结果的蒙特卡罗法作为基准解,分析了本文中的分布函数法、文献[10]中采用的蒙特卡罗法以及文献[12]中的几何近似法的计算精度和计算效率.结果表明,几何近似法具有最高的计算效率,但计算精度较低.蒙特卡罗法需要跟踪较多的能束数以达到较高的精度,计算耗时.与蒙特卡罗法相比,本文采用的分布函数法在相同发射能束数条件下的计算时间小于蒙特卡罗法计算时间的1/2,且计算精度高于蒙特卡罗法.当各物点发射能束数为50时,辐射图像各像素强度值具有很高的计算精度,平均相对误差为0.68%.本文中构建的基于分布函数辐射成像算法,相对于文献中几何近似法具有很高的计算精度,同时能够弥补蒙特卡罗法的计算耗时问题,具有优良的计算特性.
[1] 周怀春. 炉内火焰可视化检测原理与技术[M]. 北京:科学出版社,2005.
Zhou Huaichun.[M]. Beijing:Science Press,2005(in Chinese).
[2] Hossain M M,Lu G,Sun D,et al. Three-dimensional reconstruction of flame temperature and emissivity distribution using optical tomographic and two-colour pyrometric techniques[J].,2013,24(7):074010.
[3] 谢正超,王 飞,张海丹,等. 基于可见光-近红外多光谱图像的火焰场参数重建[J]. 燃烧科学与技术,2016,22(6):552-557.
Xie Zhengchao,Wang Fei,Zhang Haidan,et al. Simultaneous reconstruction of three dimensional field parameters based on the visible and near-infrared multi-spectral flame images[J].,2016,22(6):552-557(in Chinese).
[4] Zhou H C,Lou C,Cheng Q,et al. Experimental investigations on visualization of three-dimensional temperature distributions in a large-scale pulverized-coal-fired boiler furnace[J].2005,30(1):1699-1706.
[5] Liu D,Yan J,Wang F,et al. Experimental reconstructions of flame temperature distributions in laboratory-scale and large-scale pulverized-coal fired furnaces by inverse radiation analysis[J].,2012,93:397-403.
[6] Zhao W,Zhang B,Xu C,et al. Optical sectioning tomographic reconstruction of three-dimensional flame temperature distribution using single light field camera[J].2018,18(2):528-539.
[7] Qi H,Shi J W,Su Y X,et al. Soot temperature measurement within 3D flame by light-field imaging based on wave optics theory[J].,2021,138:106419.
[8] Floyd J. Computed Tomography of Chemilumines-cence:A 3D Time Resolved Sensor for Turbulent Combustion[D]. London:Imperial College London,2009.
[9] Floyd J,Geipel P,Kempf A M. Computed tomography of chemiluminescence(CTC):Instantaneous 3D measurements and phantom studies of a turbulent opposed jet flame[J].2011,158(2):376-391.
[10] Cai W,Li X,Ma L. Practical aspects of implementing three-dimensional tomography inversion for volumetric flame imaging[J].,2013,52(33):8106-8116.
[11] Li X,Ma L. Volumetric imaging of turbulent reactive flows at kHz based on computed tomography[J].,2014,22(4):4768-4778.
[12] Wang J,Song Y,Li Z H,et al. Multi-directional 3D flame chemiluminescence tomography based on lens imaging[J],2015,40(7):1231-1234.
[13] Modest M F.r[M]. USA:Academic Press,2003.
Radiative Imaging Model of Three-Dimensional Flame and Its Construction Method
Zhang Jie,Cheng Yong,Huang Zhifeng
(School of Power and Mechanical Engineering,Wuhan University,Wuhan 430072,China)
The temperature field measurement method based on radiative images has attracted wide attention because of its simplicity and no interference to the measured object. To obtain the relationship between the three-dimensional flame emission and the two-dimensional radiative image,an accurate radiative imaging model is necessary,and this is a prerequisite for the accurate temperature field measurement. The lens imaging model based on the point spread function can take into account the different imaging characteristics of the emission points inside and outside the focal plane,which is suitable for different combustion objects and radiative imaging systems. Aimed at the disadvantages of the existing construction method for imaging models in terms of computing accuracy or time consumption,an improved construction method to establish the radiative imaging model is developed by analyzing the energy distribution function of emission points on the image plane. A simplified three-dimensional flame is taken as a research object,and the radiative images obtained using different methods are compared and analyzed. Results show that the improved method has a good computing accuracy,and the computing efficiency is higher than that of the Monte Carlo method.
three-dimensional flame;radiative image;radiative imaging model;point spread function
TK311
A
1006-8740(2022)03-0347-08
2021-01-28.
国家自然科学基金资助项目(52076155,51676142).
张 杰(1997— ),男,硕士研究生,jie.zhang@whu.edu.cn.
黄志锋,男,博士,副教授,zfhuang@whu.edu.cn.
10.11715/rskxjs.R202101020
(责任编辑:武立有)
