基于偏移最小和的LDPC译码改进算法
2022-06-25陈发堂李贺宾李平安
陈发堂, 李贺宾, 李平安
(重庆邮电大学通信与信息工程学院, 重庆 400065)
scheduling
0 引 言
低密度奇偶校验码(low density paritycheck, LDPC)是1963年由Gallarger提出[1],后又被MacKay和Neal研究的线性分组码[2]。LDPC码的校验矩阵具有稀疏特性,其码长与复杂度呈线性关系,当码长足够长时,其性能可以接近理论香农极限[3],目前已经被多种通信标准所采用[4-6]。
LDPC码可以使用消息传递性算法迭代译码,该算法可以被分类为最优、准最优和次优。最优迭代译码由置信传播(belief propagation, BP)算法[7-8]执行,代价是复杂度增加、计算不稳定以及对热噪声估计误差的依赖。最小和(min-sum, MS)算法[9]执行次优迭代译码,比BP算法简单,并且独立于热噪声估计误差。MS算法的次优性是由于对校验节点消息的高估,造成了译码性能的损失。为了恢复MS算法相对于BP算法的性能损失,学者们提出了不同的优化算法,称这种算法为准最优算法。准最优算法的性能既非常接近BP算法,同时又保留了MS算法的主要特征,即低复杂度和相对于噪声方差估计的独立性。最基本的校正优化算法是归一化最小和(normalized min-sum,NMS)算法和偏移最小和(offset min-sum,OMS)算法,分别通过引入归一化因子和偏移因子来修正校验节点消息的幅度,提高译码性能[10-11]。文献[12]利用参数估计理论对MS算法进行改进,使用文献[13]中的线性最小均方误差(linear minimum mean square error,LMMSE)准则提出LMMSE-MS算法,该算法使用黄金分割搜索算法对参数进行优化,在增加少量复杂度的情况下,提高译码性能。文献[14]在OMS算法的基础上,提出了一种基于新型偏移因子的MS(new offset min-sum,NOMS)算法,该偏移因子通过最小均方误差估计过程公式化,然后通过优化均方误差获得最优的偏移因子值,使用该偏移因子可以提高算法的译码性能和收敛速度。文献[15]在NMS算法的基础上,提出了基于密度进化(density evolution,DE)理论[16]的DE-NMS算法,该算法通过密度进化理论求出归一化因子序列,通过对归一化因子序列做加权平均处理得到更精确的归一化因子以提高译码算法的译码性能。
虽然以上优化算法都提高了译码性能,但在校验节点的更新过程中没有考虑第一最小值和第二最小值的区别。因此,译码性能有待进一步提高。本文在OMS算法的基础上提出了一种基于次序统计量的OMS(order statistics OMS, OR-OMS)算法,使用两个不同的偏移因子分别对第一最小值和第二最小值进行修正,利用次序统计量理论推导出两个偏移因子的值,并且使用分层调度的消息传递方式。仿真结果表明所提算法与其他改进的MS算法相比,拥有更好的译码性能和收敛速度。
1 BP算法及其改进算法
令H=[hmn]为LDPC码的校验矩阵,ρ和γ分别为其行重和列重。变量节点集合N(m)={n:hmn=1}代表校验矩阵第m行中所有的非0元素;校验节点集合M(n)={m:hmn=1}代表校验矩阵第n列中所有的非0元素;N(m) 定义为集合N(m)中除了第n个元素以外的所有元素;M(n)m定义为集合M(n)中除了第m个元素以外的所有元素。令c={c0,c1,…,cN}为经过编码后的二进制LDPC码字,经过BPSK调制后得到传输序列x={x0,x1,…,xN},其中xn=1-2cn(n=1,2,…,N)。传输序列经过加性高斯白噪声(additive white Guassian noise, AWGN)信道传输后得到接收序列y={y0,y1,…,yN},其中yn=xn+vn,vn为均值为0、方差为N0/2的高斯白噪声。
1.1 BP算法
BP译码算法的译码过程以校验矩阵H为基础,校验矩阵中的每一个非0元素在Tanner图[17]中分别代表一条边,对数似然比(log likelihood ratio,LLR)消息沿着Tanner图中的边在变量节点和校验节点之间进行迭代。在每一次迭代的过程中,首先将变量节点消息传递给校验节点并更新校验节点消息,然后将更新后的校验节点消息传递给变量节点更新变量节点消息,接着进行下一次迭代,直到达到最大迭代次数或者得到正确码字。BP算法译码过程如下。
(1)初始化
将校验矩阵中每一个非0元素hmn对应的变量节点消息Zmn初始化为接收到的信道消息:
(1)
(2)迭代处理
步骤 1校验节点消息更新(C2V)
(2)
式中:i为第i次迭代过程。
步骤 2变量节点消息更新(V2C)
(3)
步骤 3译码判决
(4)
硬判决规则
(5)
(3)终止准则

1.2 MS算法
BP算法是一种理想算法,在实现过程中有两个难点:一是在式(1)中,噪声方差应该是已知的,但是在实际应用中很难估计噪声的精确值,尤其是当信噪比比较低时,噪声估计的偏差将极大地恶化译码性能。二是式(2)的计算过于复杂,不利于硬件实现。
针对第二个问题提出了MS算法,其C2V过程简化为
(6)
MS算法将C2V过程中的非线性计算修改为比较过程,计算复杂度大大降低。
1.3 OMS算法
虽然MS算法降低了译码复杂度,但在C2V过程中扩大了校验节点消息的幅度值,导致译码性能损失。OMS算法通过使用偏移因子对式(6)的结果进行修正,其C2V为
(7)
偏移因子可以通过下式获得:
β=E(|L2|)-E(|L1|)
(8)
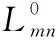
2 提出的OR-OMS算法
2.1 次序统计量理论
设X1,X2,…,XN为N个独立、同分布的随机变量,概率密度函数(probability density function, PDF)为f(x),累积分布函数(cumulative distribution function, CDF)为F(x)。通过递增的顺序排列这些变量,获取相应的次序统计量排序后的结果记为X1:N,X2:N,…,XN:N,其中X1:N为最小值,XN:N为最大值[18]。X1:N,X2:N,…,XN:N中第i个次序统计量Xi:N的PDF为

(9)
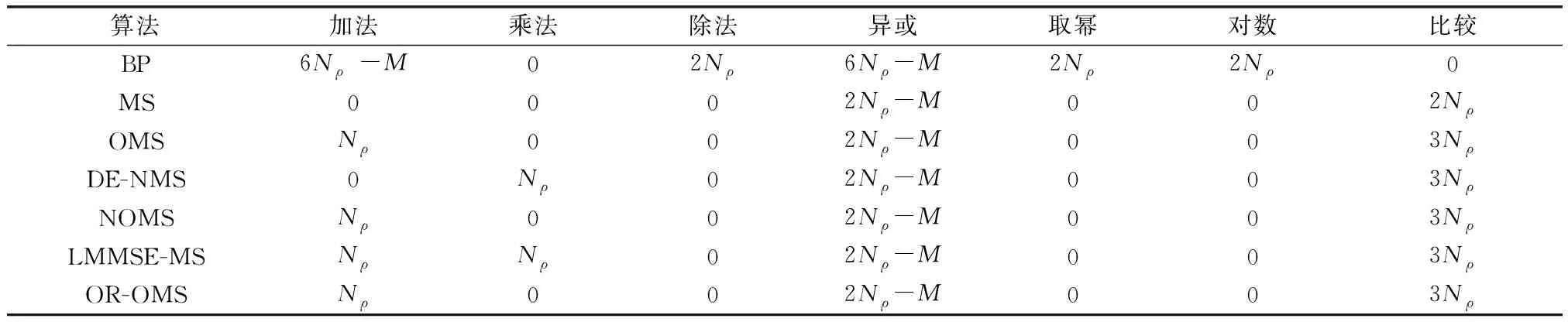
Xi1:N,Xi2:N,…,Xik:N(1≤i1 (10) (11) (12) 式中:β1和β2分别为第一最小值偏移因子和第二最小值偏移因子;L21和L11是在n≠index的情况下分别通过式(11)和式(2)获取;L22和L12是在n=index的情况下分别通过式(11)和式(2)获取。 (13) Xi的CDF为 (14) 根据式(9),集合{Xi}的第一最小值的PDF为 fX1:ρ(x1:ρ)=ρ(1-FXi(x1:ρ))ρ-1fXi(x1:ρ) (15) 集合{Xi}的第二最小值的PDF为 fX2:ρ(x2:ρ)=ρ(ρ-1)FXi(x2:ρ)(1-FXi(x2:ρ))ρ-2fXi(x2:ρ) (16) 因此,E(|L21|)和E(|L22|)的计算公式为 (17) (18) 在给定信噪比Eb/N0和码率的情况下,根据式(17)和式(18)可以求出E(|L21|)和E(|L22|)的值。同时可以得到E(|L2|)的表达式为 E(|L2|)=pE(|L21|)+(1-p)E(|L22|) (19) 式中:p为变量Xi为集合N(m)第一最小值的概率,p=1/ρ。 接下来开始推导E(|L11|)和E(|L12|)的表达式,当n=index时,根据式(2)可知L12的表达式为 (20) (21) 由式(21)可以得到E(|L12|)的表达式为 (22) 很明显可以看出,式(22)只适用于ρ值较小的情况,当ρ值过大时,计算过于复杂,很难计算出实际值。此处可以借助大数定理[19]对E(|L12|)的值进行估计,大数定理的定义如下: (23) 根据上述定理,可以证明当重复次数非常大时,|L12|的平均值最终会收敛于E(|L12|)。由此可以得出E(|L12|)具体估计过程如下: 步骤 1生成一组满足式(14)分布的随机变量X1,X2,…,Xn。 步骤 2找出这组随机序列的最小值Xmin。 步骤 3通过式(20)计算L12。 步骤 4重复上述过程,直至达到最大重复次数。 步骤 5计算E(|L12|)的值。 在实际应用中,当ρ值较小时可以使用式(22)计算E(|L12|)的值;当ρ值较大时,通过大数定理估计出E(|L12|)的值。 对于E(|L11|)的计算,如果通过次序统计量进行推导,从E(|L12|)的计算可以看出,E(|L11|)的计算会更加复杂。可以通过E(|L1|)、E(|L12|)对E(|L11|)进行求解,由式(19)可以得出 E(|L1|)=pE(|L11|)+(1-p)E(|L12|) (24) (25) 由式(24)和式(25)可知,只要计算出E(|L1|)就可以得到E(|L11|),根据式(2)可以得到E(|L1|)的计算公式如下: (26) 为了方便计算E(|L1|),定义 (27) 由泰勒级数可知 (28) 因为式(28)中α,α3,α5,…符号相同,所以 (29) 令μk=E(|α|k),因为{Xi}为独立、同分布,所以 (30) 通过式(13)和式(30)可以计算出对应的μk,由式(29)可知 (31) 一般取式(31)的前几项就可以估算出E(|L1|)的值,然后通过式(25)可以计算出E(|L11|)的值,进而可以求出最优的β1和β2的值。校验节点消息更新由式(7)可以优化为 (32) 传统OMS算法的消息传递采用洪泛(flooding)调度[20]方式,所有校验节点和变量节点消息并行传播,每次迭代更新的外部消息只能用于下一次迭代过程,外部消息利用率低。为了充分利用新产生的外部消息,提出的OR-OMS算法采用分层调度[20]的消息传递方式,在迭代的过程中一次只更新一个校验节点消息,然后将新产生的校验节点消息传递给与它关联的变量节点。文献[21]已经证明分层调度相比于洪泛调度收敛速度提升一倍,并且没有增加复杂度。 针对OR-OMS算法设计了合适的分层译码结构,如图1所示。图中FIFO代表先入先出(first input first output)。 首先将每一层的V2C消息并存于FIFO,并且将V2C消息的符号进行存储。然后对于校验节点,筛选出V2C消息的第一最小值和第二最小值及其索引,并将它们输入到C2V selector中更新校验节点信息。最后通过更新后的校验节点信息生成判决消息,同时将更新后的校验节点信息存储在C2V registers中,此时完成了一层的译码。由上可知该译码器结构不需要为判决消息分配内存空间,并且在V2C消息更新的过程中,可以直接使用C2V registers中的校验节点信息和V2C Sign FIFO中的符号值进行计算,避免对校验节点进行多次计算,降低了计算复杂度。OR-OMS算法具体流程如算法1所示。 算法 1 OR-OMS算法1:初始化所有L0mn=0,Z0mn=Z0n and Imax2:for m=1:M3: for every n∈N(m)4: 使用式(32)计算Limn5: end for6: for every n∈N(m)7: 使用式(3)计算Zimn8: 使用式(4)计算Zin9: end for10:end for11:通过式(5)得到硬判决译码结果c^=[c^1,c^2,…,c^n]12:ifA·c^T=0 or i=Imax13: 输出译码结果c^=[c^1,c^2,…,c^n]14:else15: 返回到步骤216:end if 本次仿真使用5G NR标准中的准循环LDPC(quasi-cyclic LDPC, QC-LDPC)码[22],并在Matlab平台通过模拟AWGN信道,使用二进制相移键控(binary phase shift keying, BPSK)调制方式进行传输。通过大量的仿真对所提出的OR-OMS算法性能进行评估,并将它与BP算法、MS算法、OMS算法、LMMSE-MS算法、NOMS算法、和DE-NMS算法的性能进行比较分析。 图2和图3为各译码算法在不同信噪比下的误码性能对比,图2使用的是基图1情况下的(2 176,704)QC-LDPC码,偏移因子β1和β2分别为0.304和0.373,最大迭代次数设置为20。 从图2中可以看出,OR-OMS算法、LMMSE-MS算法、NOMS算法、DE-NMS算法4种基于MS算法改进的译码算法相对于OMS算法性能都有明显的提升,其中OR-OMS算法和LMMSE-MS算法的译码性能优于NOMS算法和DE-NMS算法,但OR-OMS算法的性能更加接近于BP算法。图3使用的是基图2情况下的(3 328,640)QC-LDPC码,偏移因子β1和β2分别为0.326和0.389,最大迭代次数设置为20。 从图3中可以看出,各译码算法的译码性能相对于图2都有所提升,并且分布趋势基本相同,所提出的OR-OMS算法译码性能更加优于LMMSE-MS算法。从图2和图3可以看出在误比特率为10-5时,OR-OMS算法与OMS算法相比可以获得约0.35 dB左右的增益。 基于MS算法改进的OMS算法、DE-NMS算法、NOMS算法、LMMSE-MS算法、OR-OMS算法本质上还是MS算法。主要的区别在于OMS算法通过蒙特卡罗方法计算偏移因子的最优值。DE-NMS算法通过DE理论推导出最优偏移因子值。NOMS算法通过最小均方误差估计将偏移因子公式化,然后通过优化均方误差获得最优的偏移因子值。LMMSE-MS算法通过利用最小均方误差估计准则对校验变量信息的大小进行建模并计算估计参数,进而利用黄金分割搜索算法确定最优参数值。OR-OMS算法则通过次序统计量理论推导出第一最小值和第二最小值分别对应的最优偏移因子值。 表1为一次迭代过程中,各算法校验节点更新所需的计算复杂度。Nρ为校验矩阵中元素‘1’的总个数,M为校验矩阵的列数。从表中可以看出,BP的复杂度最高,MS算法的复杂度最低。由于在硬件实现的过程中,偏移因子的值先通过Matlab工具计算,再存储到硬件中。因此,OMS算法、DE-NMS算法、NOMS算法、OR-OMS算法的复杂度相同,LMMSE-MS算法的复杂度略高于这些算法。 表1 一次迭代过程校验节点更新计算复杂度 在硬件实现的过程中,算法的整体复杂度不仅与单次迭代过程中校验节点更新的复杂度有关,还和算法总的迭代次数有关。图4为各算法在不同信噪比下的平均迭代次数。 由于OR-OMS算法采用分层调度的信息传递方式,从图4中可以明显看出,OR-OMS算法的收敛性能最好,所需的平均迭代次数最少,其次为BP算法、OMS算法、DE-NMS算法、NOMS算法、LMMSE-MS算法的收敛性能近似,MS算法的收敛性能最差。结合单次迭代过程中校验节点更新所需的计算复杂度,可以得出在实际应用过程中,所提出的OR-OMS算法总体上来说要拥有更低的复杂度,具有实际应用价值。 本文提出了一种改进的OMS算法,所提算法针对校验节点更新过程中第一最小值和第二最小值的问题,分别使用两个不同的偏移因子对第一最小值和第二最小值进行校正,利用次序统计量理论推导出两个偏移因子的最优值,提高译码算法的译码性能。所提算法使用分层调度的消息传递方式,拥有更快的收敛速度。仿真结果表明,对于5G NR标准的QC-LDPC码,所提算法相比OMS算法拥有更好的译码性能,并且降低了译码迭代次数;与目前译码性能最好的LMMSE算法相比,在具有相似译码性能的情况下,拥有更低的计算复杂度。
2.2 OMS算法分析

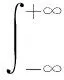
2.3 最优β1和β2值计算
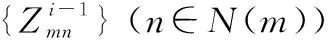




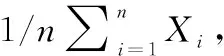

2.4 分层译码结构

3 仿真分析
4 复杂度分析
5 结 论
