任务主体二元约束下作战任务分解EVA方法
2022-06-25鲁云军陈克斌韩梦瑶
刘 乾, 鲁云军, 陈克斌, 韩梦瑶, 郭 亮
(国防科技大学信息通信学院, 湖北 武汉 430010)
0 引 言
作战任务通常是宏观的、笼统的,不便于下级作战部队理解和执行。任务分解就是把宏观的作战任务细化成若干具体、明确的子任务,使作战任务、作战目标更为清晰明确[1]。任务分解是对复杂任务求解的一种简化过程,通过合理的任务分解能够降低任务复杂度,提高任务执行效率。
目前作战任务分解方法主要有:① 以定性分析为主的任务层次分解法[2],按照一定的分解标准,将总体作战任务定性分解为特定的、层次分明的、相互独立的子任务,形成由多层级子任务构成的任务分解方案。文献[3]中通过组合运用目标分解、功能分解、作战域分解和地形区域分解等方法对登陆作战使命任务进行了多次定性分解,并提出当任务分解粒度确定时,使命分解得到的任务分解结果是类似的。在此基础上,文献[1]将作战力量作为影响任务分解的重要因素,提出了执行主体类型为标准的分解方法,并以此为依据对空间信息支援任务进行分解,构建了空间信息支援任务分解结构图。该类方法分解结果带有较大主观色彩,存在较大的随机性和不确定性;② 以定量分析为主的任务模块分解法,按照模块内强聚合、模块间弱耦合的聚类标准,将离散型多任务集合聚类为数量较少的任务模块。文献[4]引入关联内聚系数和重用内聚系数来综合描述任务关联程度,将其作为计算任务粒度的变量,并以任务粒度衡量定性分解子任务集中子任务间的耦合程度对其进行量化分解。文献[5]基于密度峰聚类(density peaks clustering, DPC)方法将任务集映射成全局任务引导树,并提取出中心子任务,而后借鉴图划分理论从互联性和紧密性两方面定义任务关联程度,对全局任务引导树的进行聚类,生成任务模块。文献[6]围绕协同作战中任务分解的优化问题,从时间、逻辑和功能3个角度对作战任务之间协同关系进行描述,构建了任务协同相关度的量化模型。文献[7]则在设计结构矩阵(design structure matrix, DSM)[8-10]的基础上提出任务结构矩阵(task structure matrix, TSM),以任务间信息流强度作为衡量任务关联度的量化指标。该类方法分解结果较为客观、科学,可控性强,但是方法应用是以已知子任务集和子任务间时序/逻辑/信息传输等关系的基础上按照任务关联强度进行的聚类,本质上规避了子任务集合的生成问题,实际应用性并不强[11-12];以智能规划为主的任务分解方法[13-16],通常将任务分解、任务分配、资源调度等任务规划问题进行统一求解,最典型的就是层次任务网络(hierarchical task network, HTN)方法,即一种基于分层抽象和领域知识的问题求解方法[17]。其任务分解过程依靠引入领域知识构建的分解复杂任务的方法模型来实现,文献[18]提出了一种考虑时间和空间约束的层次任务网络规划算法用于解决航母舰载机准备、起飞和降落方案生成。针对这类简单任务,HTN方法具备较大的优势,但是面对复杂作战任务领域时经验丰富的领域专家可能无法依靠其领域知识提供任务分解方法[19-20]。因此,考虑到领域知识对复杂作战任务分解的限制,文献[21]提出了基于目标、组织和规则(objective organization rule, OOR)框架进行任务细化的方法和步骤,将其替代领域专家知识引入HTN规划。由于HTN规划过程中,复杂任务分解方法的不唯一性[22],分解结果存在较大的多样性,无形中提高了HTN优化解搜索的复杂性,使得搜索过程变成一个多项式复杂程度的非确定性问题(non-deterministic polynominal complete problem, NPC)[23]。
综上所述可知:一是定性方法依赖指挥员的历史经验和领域专家知识,存在大量的不确定性,仅可用于简单战术级任务;二是多数定量方法仅考虑了任务和任务关系因素,忽略了任务主体的能力因素限制,与任务分解实际并不相符;三是忽略了任务主体结构特征,无法控制分解结果中子任务数量,子任务数量与任务主体下属任务个体数量不匹配。为此,本文立足现有方法缺陷与不足,综合考虑任务主体能力因素和结构特征等二元约束,提出一种由子任务集提取(extraction, E)、约束检验(verification, V)、子任务集调整(adjustment, A)等步骤递进循环形成的任务分解EVA方法。
1 任务分解问题描述及求解框架
1.1 问题描述
本文研究的作战任务分解是在已知目标任务和任务主体的基础上,依据任务主体能力属性和结构特征将目标任务分解成一定数量的子任务,同时按照一定顺序关系执行子任务,能够达成任务目标。
因此任务分解问题可描述为:已知任务主体S={S1,S2,…,Sn},其能力属性矩阵C=[C1,C2,…,Cn],Cn表示任务个体Sn的k维能力向量,目标任务为T,若存在T0={T1,T2,…,Tm},且其能力需求矩阵RC0=[RC1,RC2,…,RCm],RCm表示任务Tm的k维能力需求向量,使得S中任务个体按照某种时序关系完成T0中所有子任务后能够达成T,那么T0就是T的一个任务分解结果。同时T0还需满足如下两条约束:
约束 1子任务能力可支持约束,即分解结果中各子任务的能力需求都能够被任务主体下属某任务个体所满足,任务分解结果中不存在无法执行的子任务。即对于T0={T1,T2,…,Tm}和S={S1,S2,…,Sn},应满足∀j∈m,∃i∈n,RCjh≤Cih,h∈(1,k)。
约束 2子任务数量可支持约束,即分解结果中子任务数量不能大于任务主体下属任务个体的数量。由于任务主体的任务分解结果是其下级任务个体的任务分解对象,每个任务个体仅能受领一个目标任务,因此需从任务主体结构特征角度限制任务分解结果中子任务数量。即对于T0={T1,T2,…,Tm},应满足m≤n,其中n表示任务主体下属任务个体数量,m表示分解结果中子任务数量。
1.2 EVA方法框架
依据上述任务分解描述,作战任务分解应包括:依据目标任务生成子任务集,判断子任务集是否满足任务主体二元约束,以及在不满足约束时对子任务集进行调整等步骤。考虑到上述问题之间的内在关联性,本文在任务主体二元约束限制下,设计了作战任务分解EVA方法框架,其流程图如图1所示。
步骤 1子任务集提取(E)
步骤 1.1全局作战任务空间构建。确定作战任务层级,并对不同层级任务进行结构化建模,设计其结构化描述要素,形成层次化树状结构的任务空间。
步骤 1.2目标任务分解树提取。依据任务描述模型对目标任务进行结构化描述,通过匹配方法确定目标任务在全局任务空间的位置,并提取以目标任务为根节点,与其直接相连的下一层级任务为叶子节点的任务分解树,将分解树的最底层叶子节点集合作为子任务集。
步骤 2约束检验(V)
按照先检验约束1(子任务能力可支持约束),再检验约束2(子任务数量可支持约束)的串行检验思路,若不满足约束1,则转入步骤3.1;若满足约束1,不满足约束2,则转入步骤3.2,而后分解结束;若约束1和约束2都满足,则分解结束。
步骤 3子任务集调整(A)
步骤 3.1子任务集细化调整。针对不满足约束1的子任务提取以它为根节点的任务分解树,将该树的叶子节点集合替代根节点融入原始子任务集,并转入步骤2。
步骤 3.2子任务集量化调整。以任务模块内关联程度高、任务模块间关联程度低为优化目标,以任务模块数量可支持和任务模块能力可支持作为约束条件,构建子任务集量化调整模型并求解。
2 子任务集提取
按照上述求解策略,为构建全局作战任务空间,首先需要对任务进行描述,确定任务层级和不同层级任务的描述要素,而后依据不同层级任务间的父子关系,建立全局任务空间,并以此为依据,匹配确定目标任务在全局任务空间中的位置,获取目标任务分解树,进而完成目标任务的子任务集提取。
2.1 全局作战任务空间构建
依据美军通用联合任务清单(universal joint task list,UJTL)[24]将作战任务划分为由高至低的联合作战任务、基本作战任务和战术行动任务3类,并以3类作战任务为基础进行描述。
联合作战任务描述模型。联合作战任务是复杂任务,由联合作战部队负责执行,处于作战任务空间的最顶层。因此,联合作战任务描述模型表示为TS/B/T=〈任务序号,任务内容,任务尺度,任务类型,任务层级,任务能力需求,子任务序号〉,其中TS、TB、TT分别表示战略层、战役层、战术层联合作战任务。
基本作战任务描述模型。基本作战任务是联合作战任务的子任务,是战术行动任务的父任务,处于作战任务空间的中间层,由各军种各层级作战力量负责执行。基本作战任务描述模型表示为TF=〈任务序号,任务内容,任务尺度,任务类型,任务能力需求,父任务序号,子任务序号〉。
战术行动任务描述模型。战术行动任务是子任务,处于作战任务空间的最底层,通常对应军事行动中的战术行动,通常不可再分解。因此,战术行动任务描述模型表示为TA=〈任务序号,任务内容,任务尺度,任务类型,任务能力需求,父任务序号〉。
作战任务空间是层次化树状结构,主体按照“联合作战任务→基本作战任务→战斗行动任务”的顺序逐级细化生成的一个全局作战任务树,为目标任务分解树生成提供全局任务搜索空间。由于任务主体指挥层次的多样性,使得任务空间逐级细化过程中又存在多种分解模式,分解模式的选择主要由任务主体指挥层级结构特点所决定,具体如图2所示。
当前构建面向任务主体的作战任务空间的方法主要包括两种:一是以成熟的联合作战任务清单和任务主体指挥层级为基础,从联合作战任务清单中提取出任务主体可能承担的所有使命任务,而后将上述使命任务作为该任务主体的全局作战任务空间中的顶层根任务,提取出该根节点任务的所有叶子节点任务,并利用上述3类作战任务描述模型对上述各类型任务进行形式化描述,而后依据任务主体指挥层次特征,搭建符合任务主体指挥层级特点的全局作战任务空间;二是在缺乏成熟的联合作战任务清单的情况下,需要利用专家知识与历史经验从任务主体作战想定、演习方案等相关文书中抽取出相应数据,依托条令条例进行文本数据规范,再采用任务描述模型进行形式化描述,最后结合任务主体的指挥层次特征构建全局作战任务空间,其基本思路如图3所示。由于当前我军尚无成熟的联合作战任务清单,因此在具体实施过程中,需要大量依靠专家和指挥人员的知识和经验,利用基于人工智能的文本信息抽取工具,从大量作战文书文档资料中抽取出所需的作战任务数据信息,这也是全局作战任务空间构建的关键。
2.2 目标任务分解树提取
该方法主要解决从庞大的任务空间中快速找出与目标任务匹配度最高的作战任务。依据任务执行主体层级结构特征确定任务分解模式,并以此为基础提取出与其直接相连的下一层级任务,生成目标任务的任务分解树,实现针对特定作战任务的快速分解。具体流程如下:
步骤 1读取全局作战任务空间中联合作战任务列表的任务集TJ,基本作战任务列表的任务集TF,战术行动任务列表的任务集TA;
步骤 2将目标任务存储在集合A中,任务匹配结果存储在集合B中,任务分解树的任务集存储在集合C中,初始情况下集合A是多任务集合,集合B和C均为空;
步骤 3从集合A中随机选择一项目标任务,判断其任务类型,并按照相应作战任务描述模型进行建模,设为T0;
步骤 4将T0与相应类型的任务集进行对照比对,依次按照任务层级、任务类型、任务内容的优先顺序进行比对,检查任务集中是否存在与T0完全相同或匹配度较高的任务T1,若存在,将任务T1存入集合B中,并转入步骤6,否则转入步骤5;
步骤 5匹配搜索任务无法完成,返回由指挥人员进行人工干预,并从集合A中删除任务T0;
步骤 6依据任务执行主体结构特征,确定任务分解模式,从全局作战任务空间中提取与任务T1存在子代关系的作战任务集,存入集合C;
步骤 7输出集合C,并按照任务集中任务间父子关系生成目标任务的双层任务分解树并保存,清空集合B和C,删除集合A中的任务T0;
步骤 8如果集合A为空集,表示匹配搜索完成,否则继续进行搜索,转入步骤3。
上述匹配方法的关键是对两个作战任务进行对照比较,判断两个作战任务的匹配程度。这个问题通常可采用人工匹配、机器学习语义识别匹配、人工智能等方法,由于不是本文的重点,在这里不做赘述。
3 子任务集调整建模
按照上述求解策略,需对不满足任务主体二元约束的子任务集进行调整,包括细化调整和量化调整,其中细化调整可采用第2.2节所提出的任务分解树提取方法。本节重点研究子任务集量化调整建模。
3.1 符号说明
为准确描述子任务集量化调整问题,先定义如下符号:T表示所有子任务的集合;RT表示T中相互关联的子任务所构成的任务集合,即关联性任务集合;IT表示T中相互独立的子任务所构成的集合,即独立性任务集合;RCi表示子任务Ti的能力需求矢量,RCij表示子任务Ti的第j项能力需求值;μk是第k项能力需求的权重;S表示任务主体;n表示任务主体下属任务个体数量;Ci表示任务个体Si的能力向量,Cij表示任务个体Ci的第j项能力属性值。
3.2 任务关联程度量化
针对RT和IT的任务特征,分别引入任务支持度和任务相似度对两类任务的关联程度进行量化描述。
任务支持度是衡量RT中任务间关联程度的量化指标,可由任务间的信息支持度、态势支持度来综合计算。例如,如果任务T1是任务T2的前置任务,记任务T1信息态势输出变量out1=(io1,so1),任务T2信息态势输入变量in2=(ii2,si2),则任务T1对任务T2的支持度如下:
md12=αfi(io1,ii2)+βfs(so1,si2)
(1)
式中:fi为信息支持函数;fs为态势支持函数;α、β为支持权重;md12=md21,mdii=0。
任务模块内支持度:若某关联性任务模块由m个关联性任务构成,则任务模块内支持度为
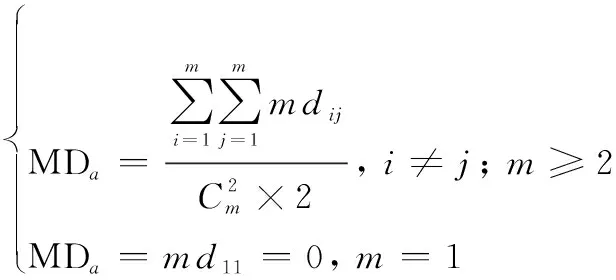
(2)
任务模块间支持度:如果某两个关联性任务模块内任务数量分别为m和n,则任务模块间支持度为
(3)
任务相似度:衡量IT中任务间关联程度的量化指标,可由IT中各任务能力需求矢量的相似接近程度计算。即IT中任务Ti和任务Tj的相似度可表示为RCi和RCj的加权闵可夫斯基距离dij,表达式为
(4)
式中:p表示阶数,通常取值p=1,2或+∞。依式(4)可得IT的加权闵可夫斯基距离矩阵(dij)N×N,归一化处理后得到归一化矩阵(sdij)N×N,其中sdii=0,N是独立性任务集中子任务数量。
任务模块内相似度:假设某独立性任务模块由n项子任务构成,则任务模块内相似度为
(5)
任务模块间相似度:如果某两个独立性任务模块内任务数量分别为p和q,则任务模块间相似度为
(6)
3.3 目标函数
子任务集调整是以调整后任务模块内关联程度最大,任务模块间关联程度最小作为优化目标。假设RT和IT两类任务集中初始子任务数量为I和J,量化调整后任务模块数量分别为P和Q,则其目标函数可表示为
(7)
式中:MDm是RT量化调整后任务模块内部支持度;MDij是RT量化调整后任务模块间支持度;SDn是IT量化调整后任务模块内部相似度;SDij是IT量化调整后任务模块间相似度;i≠j。
3.4 约束条件
(1) 任务模块能力可支持,即对于任意任务模块都存在至少一个任务执行个体,使得个体能力向量满足任务模块能力需求。
(8)
式中:RCXrh表示RT任务集中任务模块Xr的第h项能力需求值;RCYsh表示IT任务集中任务模块Ys的第h项能力需求值。
若RT的任务模块Xr有t个子任务,IT的任务模块Ys有g个子任务,则任务模块的第h项能力需求值如下:
(9)
RT中任务模块的能力需求是取模块内子任务单项能力需求的最大值,IT中任务模块的能力需求是取模块内子任务单项能力需求的累加值。
(2) 任务模块数量可支持,即子任务集量化调整后生成的任务模块数量不多于任务执行主体下属执行个体数量:
P+Q≤N
(10)
(3) 任务模块不重叠,即任意子任务只能隶属于一个任务模块,不能同时属于多个任务模块。
(4) 任务模块不为空,即任意任务模块中至少应包含一个子任务,不能为空。
4 模型求解
子任务集调整模型求解是多目标优化问题,其求解算法通常是一种多目标优化算法[25]。非支配排序遗传算法Ⅱ(non-dominated sorfing genetic algorithm-Ⅱ, NSGA-Ⅱ)由于计算速度快,能够保持种群个体多样性等优点,已经成为目前较常用的低维多目标优化算法[20]。该方法采用了精英保留策略对非支配排序产生的最佳个体进行保留。在保留过程中会产生大量相同或相似个体覆盖整个种群,容易造成早熟。该算法采用了固定的交叉、变异概率,而固定交叉概率会影响优秀个体的存在、固定变异概率会影响个体的多样性。
因此,本文在NSGA-Ⅱ算法基础上,引入任务分解粒度、改进型的精英保留策略和交叉、变异概率动态调整策略,提出一种改进NSGA-Ⅱ(improved NSGA-Ⅱ, INSGA-Ⅱ)用于模型求解以降低算法求解复杂度,避免算法早熟,保证解的多样性。
4.1 任务分解粒度
通常记为ω,且ω∈[0, 1],若任务支持度(相似度)mdij≥ω(sdij≥ω),则表示两任务间具有很强的关联性,可视为一个任务整体[26]。当ω=0时,表示子任务集中所有子任务是一个任务整体;当ω=1时,表示子任务集中每一个子任务都是一个独立的任务个体。在种群初始化之前,利用任务分解粒度ω对RT任务集的支持度矩阵、IT任务集的相似度矩阵进行降阶处理,即设定任务分解粒度ω,将支持度mdij≥ω或相似度sdij≥ω的任务Ti、Tj合并。
4.2 改进的精英保留策略
改进的精英保留策略是在传统精英保留策略的基础上,只保留经过非支配层排序后的第一支配层的全部个体,对其他支配层个体不再按照支配层级由高到低进行保留,而是均按照一定的比例进行保留,并确保所保留的个体数量与初始种群个体数量相同。改进的精英保留策略能够保证生成的子代种群的多样性,避免算法过早收敛[27]。针对改进的精英保留策略本文设计了如下不同支配层级子代保留数量的计算公式:
(11)
式中:K表示父代和子代合并后的种群经过非支配层排序后支配层的数量;mi表示第i层支配层应保留的个体数量;m0表示第一层支配层后代的数量;m表示初始种群的染色体数量。如果在经过多次交叉、变异计算后第一支配层级个体数量大于初始种群中染色体数量时,则采用传统精英保留策略,对第一支配层内个体进行拥挤度计算,仅保留第一支配层中较优的m个个体。
4.3 交叉、变异概率动态调整策略
交叉和变异是种群进化的关键。交叉概率高容易产生新的个体,但高适应度的个体也容易被破坏,交叉概率低难以搜索到高适应度的个体。变异概率高能够提高算法局部搜索速度,保持种群多样性,避免早熟,变异概率低能够保持种群的稳定性收敛快。传统方法通过人为设定固定的交叉概率和变异概率,但无法适应种群进化的动态变化性[28]。
交叉概率动态调整策略。在种群进化初期,种群多样性好,故只需要较低的交叉概率保持种群多样性,随着代数增加,种群中相同/相似个体数量不断增加,需要逐步提高交叉概率保证种群多样性。交叉概率是随着进化代数增加不断增加。其计算公式如下:
(12)
变异概率动态调整策略。在种群进化初期,可以通过加大变异概率,提高算法的搜索速度,随着代数不断增加,种群个体都拥有比较高的适应度,因此需要降低变异概率,保持种群的稳定性,提高收敛速度。变异概率是随着进化代数增加而不断降低。其计算公式如下:
(13)
式中:PC 0和PM 0表示初始交叉概率和变异概率;GEN表示设定的遗传代数;gen表示当前的遗传代数;α和β均为常量,分别取1.5和0.05。
4.4 染色体编码方式
考虑到目标函数存在的4项约束条件,为简化求解过程降低约束检验的复杂性,本文采用实数编码方式,假设子任务集数量为I,任务模块数量为J,则染色体基因长度为I,且按照子任务编号由小到大进行排序,如果某基因元素的取值为a,则表明该基因代表的子任务将聚类到第a个任务模块。为解决染色体编码的非冗余性,在按照子任务编号顺序逐一编码时,设定当i
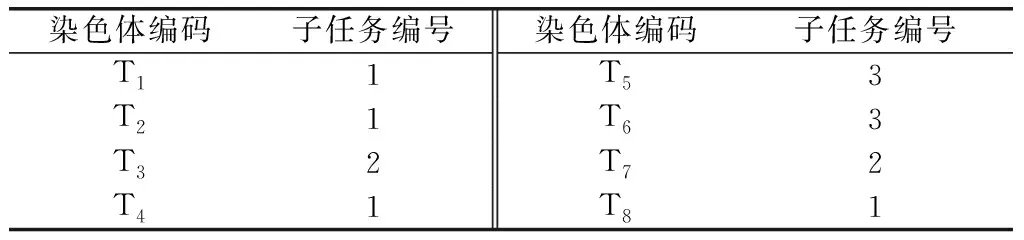
表1 染色体编码示例
上述编码方式能够保证随机生成的染色体满足任务模块数量可支持性和任务模块不重叠的约束条件,因此随机生成染色体后仅需检验任务模块能力可支持性和任务模块不为空。
4.5 遗传算子
交叉算子。采用“单点交叉”模式,在选择交叉点时,从两个染色体起始位开始,当第一次出现元素不同时,以该基因点作为交叉点,将基因点右侧的部分染色体进行交叉。该交叉算子能保证交叉后染色体始终满足任务模块不重叠、任务模块不为空和任务模块数量可支持性约束,还需检验是否符合染色体编码方式,且满足任务模块能力可支持性约束,如果不满足,则将交叉点右移一位,继续进行交叉,直到满足约束。如果始终无法满足约束,则交叉失败,重新随机选择染色体进行交叉。
变异算子。鉴于染色体编码的特殊性,在变异点选择上,应随机选择除起始点和任务模块中仅有一个子任务的基因点之外的其他基因点作为变异点。在变异值选择上,应从基因元素定义域中随机选择除原始值以外的任意值,并检验是否符合染色体编码方式,且满足任务模块能力可支持性约束,如果某子代不符合约束或编码方式,则随机选择其他子代,若都不符合,则重新选择变异点。
4.6 改进型NSGA-Ⅱ算法流程
步骤 1设定任务分解粒度ω,将支持度m dij≥ω或相似度s dij≥ω的任务Ti、Tj合并;
步骤 2种群初始化,种群规模为s;
步骤 3遗传运算,运用交叉、变异概率动态调整策略,对随机选择种群个体进行交叉、变异;
步骤 4将初始种群与交叉子代、变异子代合并,运用改进的精英保留策略保留数量为s的个体作为第一代子代种群;
步骤 5将第一代子代种群按照步骤3和步骤4进行循环操作,直至满足遗传结束条件。
5 仿真与分析
5.1 仿真实验
本节对上述子任务集量化调整模型及求解算法进行实验分析。假设某任务主体S其下属任务个体数量为6,能力维度为10,其能力属性矩阵如表2所示。
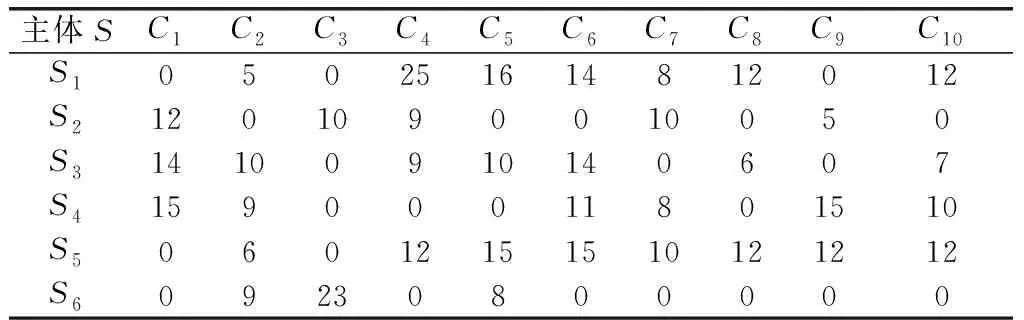
表2 能力属性矩阵
任务主体S受领作战任务T,其子任务数量为19,且RT和IT中子任务数量分别为13和6。利用任务支持度和任务相似度计算公式,且假设加权闵式距离计算阶数p=2,可得RT的支持度矩阵(mdij)13×13和IT的相似度矩阵(sdij),如表3和表4所示。假设ω=0.7,则RT={T1,T2,T3, (T4T10),T5, (T6T7), (T8T9),T11, (T12T13)},IT={(T14T17), (T15T18), (T16T19)},其任务能力需求矩阵如表5所示。
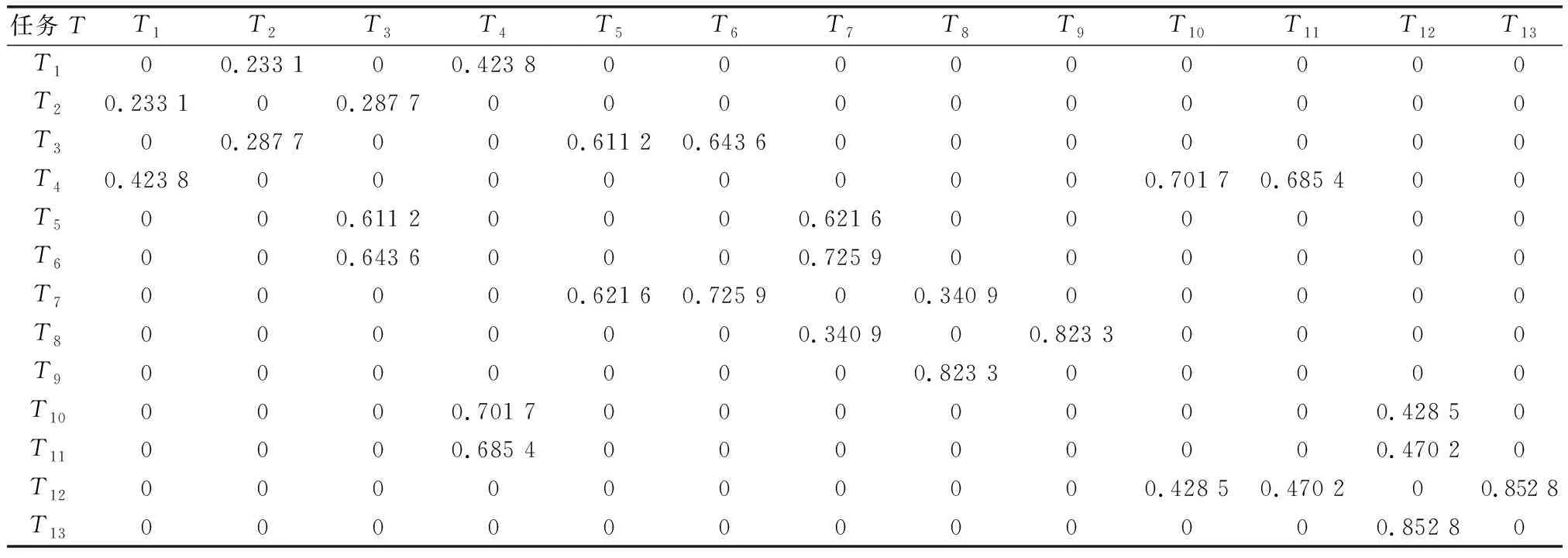
表3 支持度矩阵

表4 相似度矩阵
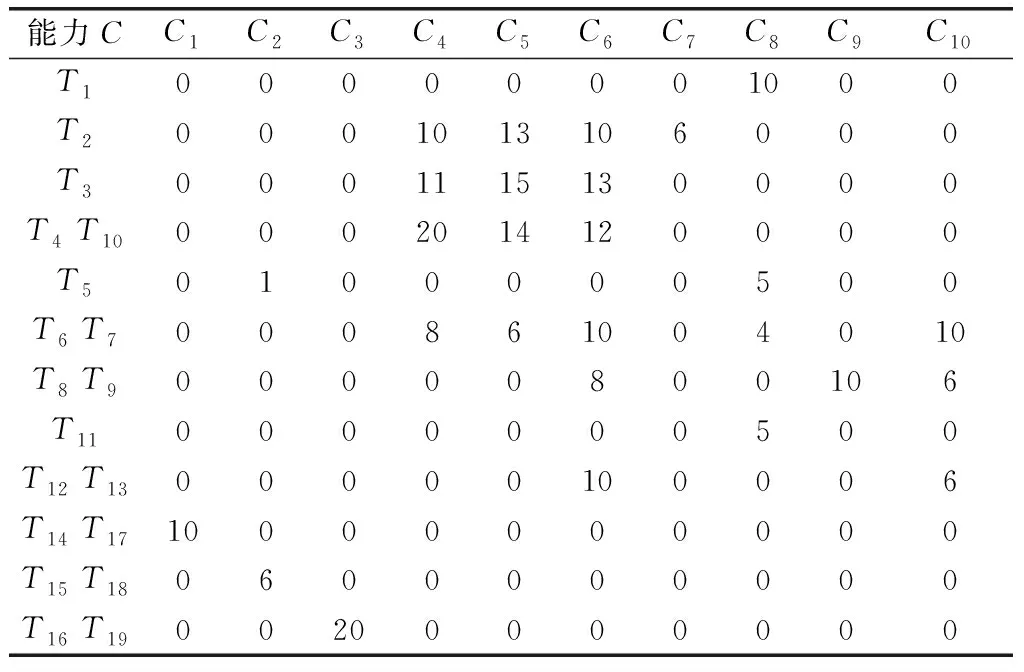
表5 任务能力需求矩阵
参数设置:种群规模为300,遗传代数为20,交叉、变异比例初始值分别取0.8和0.007。仿真实验参数主要以文献[29-30]中遗传算法和NSGA-Ⅱ算法所指定的参数值为基础,通过调整算法参数值进行了多次仿真实验,综合考虑算法计算速度和解集质量等因素而确定。
仿真实验分别独立运行20次,取模块内支持度最大、模块间支持度最小的染色体作为任务集RT的调整结果,取模块内相似度最大、模块间相似度最小的染色体作为任务集IT的调整结果,如表6和表7所示。表6中SDinner、SDinter分别表示各模块内部相似度累加和、各模块间相似度累加和,表7中MDinner、MDinter分别表示各模块内部支持度累加和、各模块间支持度累加和。

表6 IT量化调整结果
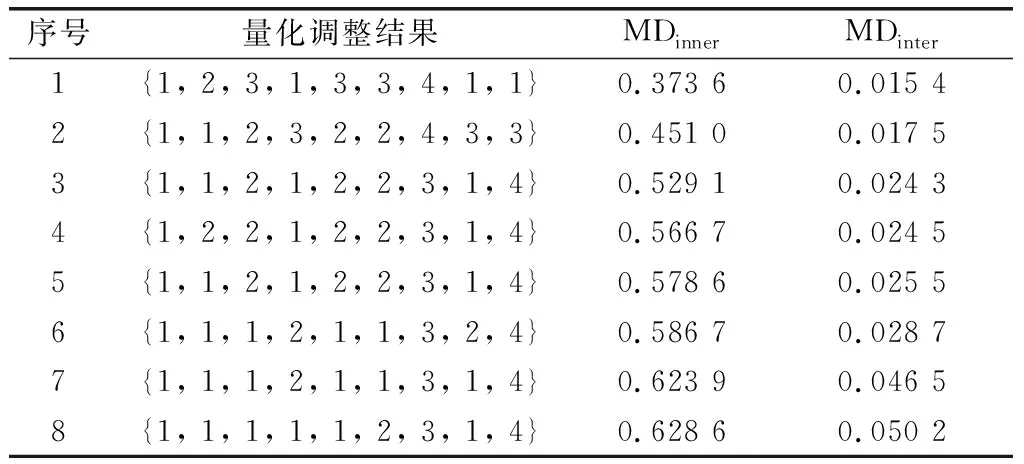
表7 RT量化调整结果
仿真实验结果表明:运用INSGA-Ⅱ算法求解多目标优化问题将生成一个优化解集,解集中的每一个优化解都是该多目标优化问题的最优解。对于本文研究的双目标优化模型,考虑到存在的任务模块能力可支持、任务模块数量可支持、任务模块不重叠和任务模块不为空等4个约束条件,对于独立性任务集IT的量化调整结果仅存在一个最优解,而对于关联性任务集RT则存在多个最优解。而在实际应用上,需要指挥员考虑影响使命任务达成的关键性子任务、战场对抗条件、作战单元协同难易程度等多方面因素从最优解中选取一个最优解作为实际作战任务分解方案。
5.2 算法对比分析
为比较本文所提INSGA-Ⅱ算法优势,选取NSGA-Ⅱ、基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition, MOEA/D)作为对比算法,围绕第5.1节中任务集RT的量化调整过程进行3组实验,每组实验独立运行20次,分别取每组实验中最优解的两个优化目标MDinner和MDinter的平均值进行比较分析,如表8所示。从表中可以看出在3组实验中,第3组实验中INSGA-Ⅱ算法与第2组实验中MOEA/D算法结果相同;第2组实验中INSGA-Ⅱ算法与第3组实验中MOEA/D算法结果接近,但相对较优。从其他实验结果来看,INSGA-Ⅱ算法相比较NSGA-Ⅱ和MOEA/D算法均具有一定优势。
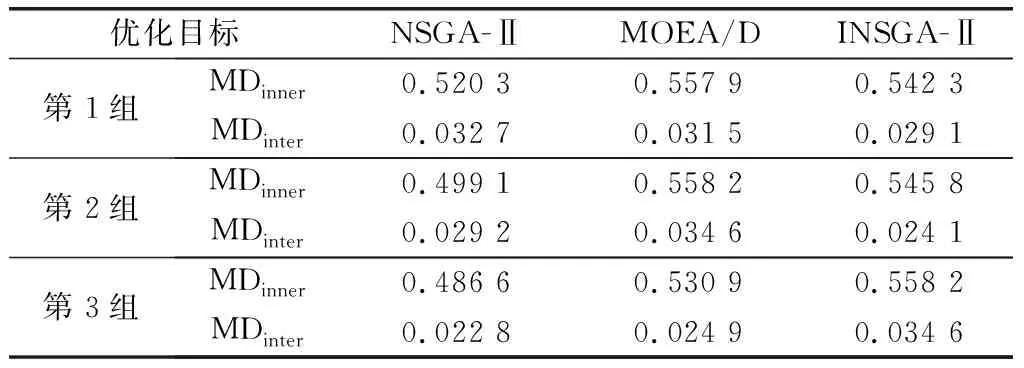
表8 各算法结果比较
以第1组实验为例,生成3种算法最优解的散点分布图(图4)来看,在处理低维多目标优化问题上,MOEA/D和INSGA-Ⅱ算法在解集的分布性上均优于NSGA-Ⅱ。而INSGA-Ⅱ算法在解集的收敛效果上要优于MOEA/D和NSGA-Ⅱ算法。因此,决策者可结合战场实际,从INSGA-Ⅱ算法生成的Pareto解集中选择任务量化调整方案,以指导后续任务规划工作。
5.3 算法性能分析
本文主要选取覆盖率指标(set coverage, SC)[31]和时间性能指标对3类算法的性能进行分析。其中SC解集覆盖率指标是比较各种算法产生的Pareto解集之间的支配关系。通常由两个算法产生的Pareto解集的支配比例来衡量。3种算法的SC覆盖率指标如表9所示。可以看出INSGA-Ⅱ的覆盖率指标优于另外两种多目标优化算法,表明INSGA-Ⅱ算法具有较好的多样性和收敛性,解集质量较高。
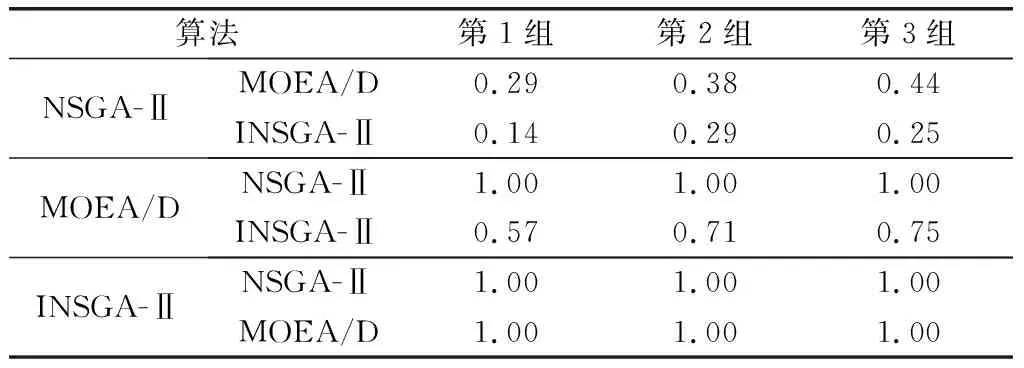
表9 各算法覆盖率指标值
考虑到任务分解过程在作战筹划阶段的时效性要求,分解算法的时耗指标也是评价算法性能的重要指标。本文采用箱图形式统计分析3种算法的消耗时间,如图5所示。其中,INSGA-Ⅱ平均耗时68.096 3 s、MOEA/D平均耗时77.797 8 s、NSGA-Ⅱ平均耗时73.859 1 s。从图5中可知,INSGA-Ⅱ耗时较少,MOEA/D耗时较多。INSGA-Ⅱ算法比传统NSGA-Ⅱ算法在时耗上降低了7.8%,其原因在于通过引入任务分解粒度ω减少了子任务数量,降低了算法的运算量,同时通过运用改进的精英保留策略按比例保留子代数量,减少了传统精英保留策略中拥挤度计算量。虽然单次运行节省时间仅为5 s,但为避免局部最优通常需要多次运行取最优解,因此计算60次后能节省5 min。
6 结 论
本文基于传统分解方法缺陷,引入数量可支持性约束和能力可支持性约束,对任务分解问题进行了描述与分析,提出了一种任务主体二元约束下作战任务分解EVA方法,并围绕子任务集提取和子任务集调整方法进行设计。针对子任务集提取,设计了全局任务空间的结构化描述方式和目标任务分解树提取方法;针对子任务集调整,构建了子任务集量化调整数学模型,并引入任务分解粒度,提出一种基于改进型精英保留策略和交叉、变异概率动态调整策略的INSGA-Ⅱ算法;最后,通过仿真实验验证INSGA-Ⅱ相较于传统多目标优化算法在解集收敛性、多样性和时间性能上的优势,能够支撑指挥员依据战场实际选择合适的子任务集量化调整方案。
