基于自适应未知输入观测器的多故障快速重构

高 升, 马广富, 郭延宁,*

(1. 哈尔滨工业大学航天学院, 黑龙江 哈尔滨 150001; 2. 中国科学院沈阳自动化研究所, 辽宁 沈阳 110016)

0 引 言

现代工程系统变得越来越复杂的同时,人们对高可靠性和安全性的需求也日益增加。由于系统经常受到各种类型的外部环境的影响,导致系统易发生故障,从而影响系统的可靠性,甚至出现系统崩溃的情况。因此,及时地发现故障并定位故障就显得尤为重要。近10年来,现代工程系统的故障诊断技术已成为一个重要且热门的研究课题,并已成功应用于航空航天系统、工业机器人系统、水下航行器系统等。

故障在实际工程中是非常常见的,而故障诊断的目的便是检测故障的发生,并进一步确定其位置。在最近的一篇综述文章中,故障诊断方法被分为4类,即基于解析/数学模型的方法、基于信号的方法、基于知识的方法和混合方法。基于模型的方法是研究最早、成果最多的方法,其中基于观测器的故障诊断方法更是受到学者们的青睐,也得到了大量应用。Tan等人指出,基于观测器的故障诊断就是将系统的输出与基于系统模型设计的观测器的输出进行比较,形成残差,并将其作为故障诊断的依据。虽然该方法和生成的残差可以用于检测和定位故障源并产生警报信号,但不能提供故障幅度的信息。因此,需要应用故障重构方法进一步提供更深层次的故障信息。

近年来,基于观测器的故障重构研究成果颇丰,如自适应观测器(adaptive observers, AO)、未知输入观测器(unknown input observers, UIO)、滑模观测器(sliding-mode observers, SMO)、神经网络观测器(neural-network observers, NNO)和广义系统观测器(descriptor system observers, DSO)等。文献[11-12]针对非线性系统设计UIO将系统未知输入干扰与故障完全解耦,从而达到故障重构的目的,但其主要问题是需要满足观测器匹配条件,许多实际系统难以满足。文献[13]针对非线性系统设计SMO完成系统的故障重构任务,当扰动和故障分布矩阵满足一定条件且抖振效应可以忽略时,该方法可以获得较高的故障重构精度。基于NNO的方法也可以达到故障重构的目的,但其参数的随机性在一定程度上限制了其应用。Gao等人提出一种基于广义观测器的故障重构方法,该方法将传感器故障与系统状态向量组合构建增广系统,从而达到多故障重构的目的,但其未考虑测量噪声对故障重构结果的影响。

在过去的几十年里,许多学者对基于AO的故障重构方法进行了研究,并在非线性系统中取得了一些重要的成果。这些方法考虑了传统AO中固有的严格正实(strictly positive real, SPR)假设条件,这比观测器的匹配条件更为保守。Zhang等人基于优化的思想设计了一种快速AO以提高故障重构的性能,并拓宽了AO的应用范围。文献[19]采用AO来重构故障,该方法需要知道故障与故障导数的上界。

为了进一步改善AO的估计性能及应用范围,学者们围绕自适应UIO (adaptive UIO, AUIO)进行了大量的研究工作,得到了丰富的研究成果。起初是在UIO的基础上引入自适应算法,用于估计常值的或者随时间变化的未知参数故障,达到故障检测与隔离的目的。然后,为了进一步实现执行器故障和传感器故障的同时估计,学者们将传感器故障视为一种增广状态,在此基础上设计AUIO完成多故障估计任务。文献[22-23]提出了可用于非线性系统鲁棒故障估计的AUIO,但没有考虑故障估计的性能,即故障估计的快速性问题。文献[24-26]虽然考虑了故障估计的性能但未考虑测量噪声对重构结果的影响。与此同时,这些研究成果均未考虑执行器故障耦合于非线性函数的情况。

基于上述分析,本文提出一种基于AUIO的多故障快速重构方法(fast AUIO, FAUIO),该方法同时考虑了未知输入干扰和测量噪声干扰,并能同时重构系统中的执行器故障和传感器故障。与已有方法相比,本文创新性地考虑一类非线性函数中耦合执行器故障的非线性系统,并设计相应的执行器故障解耦方法。为了尽可能达到鲁棒故障重构的目的,本文基于优化的思想设计H性能指标,通过线性矩阵不等式求解所设计的快速自适应未知输入观测器参数。最后,将本文方法应用于单关节柔性机器人算例,实现了一类非线性系统的多故障重构,验证了该方法的有效性。

1 问题描述

考虑下面带有执行器故障和传感器故障的非线性动态系统,其中执行器故障耦合于非线性函数中:

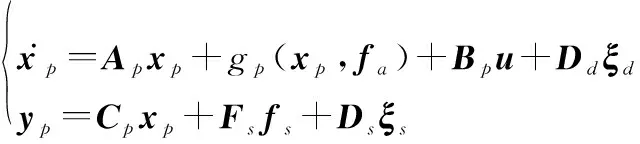
(1)

式中:∈,∈,∈分别表示系统的状态向量、测量输出向量和控制输入向量;∈表示未知输入干扰;∈表示测量噪声干扰;∈和∈分别表示系统的执行器故障和传感器故障;(,)表示系统的非线性函数;∈×,∈×,∈×,∈×,∈×,∈×是已知的适维常矩阵,并假设矩阵和为列满秩矩阵。

不失一般性,对非线性函数(,)做如下分解:

(,)=+,2(,)

(2)

式中:是已知的适维常矩阵且列满秩。

系统是可观测的,即(,)可观。

未知输入干扰和测量噪声干扰有上界但未知,的一阶导数存在且有界,即

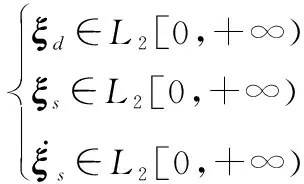
(3)

,2(,)为Lipschitz非线性项, 满足

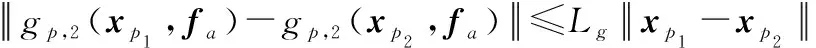
(4)

式中:为Lipschitz未知常数。

执行器故障中的元素都是连续可微函数,即可定义为时间的多项式函数,满足

()=+++…+-1-1

(5)

式中:=1,2,…，;是未知的常数且已知;=1,2,…,-1。

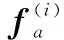
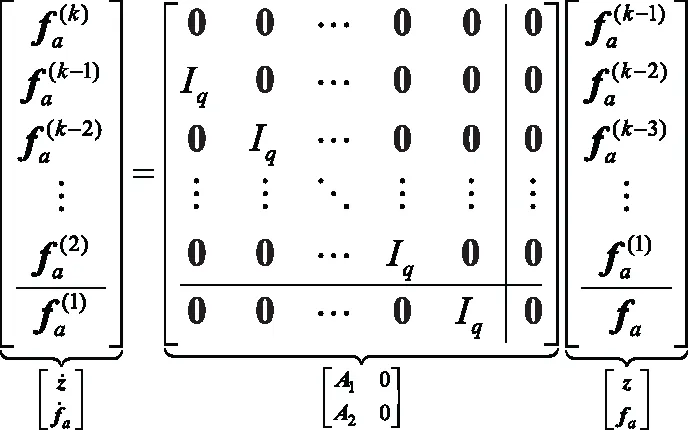
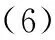
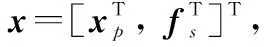
(7)

式中:=[,×];=[,×;=[,];=。

显然,新的增广状态向量包含传感器故障。因此,如果可以为系统设计一个有效的观测器,则可以直接得到执行器故障(解耦于非线性函数)和传感器故障的准确估计。

2 多故障重构观测器设计

针对增广系统,考虑如下形式的FAUIO:

(8)

其中,根据文献[12]和文献[23]给出的结论,矩阵,,和应满足如下等式:

(9)

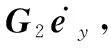
因为矩阵[,]是列满秩矩阵,因此逆矩阵([,][,])存在,令

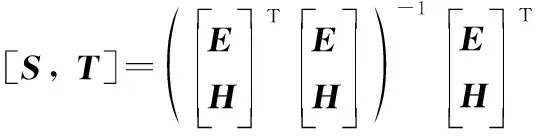
(10)

因此,式(9)中的等式+=+成立。

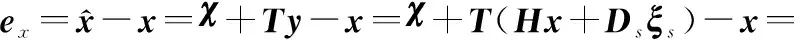
(11)

进一步可以得到

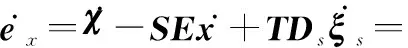
(12)

由于=-和=+成立,因此有

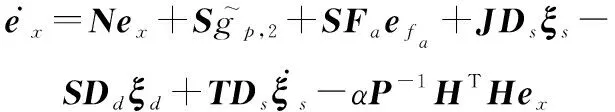
(13)

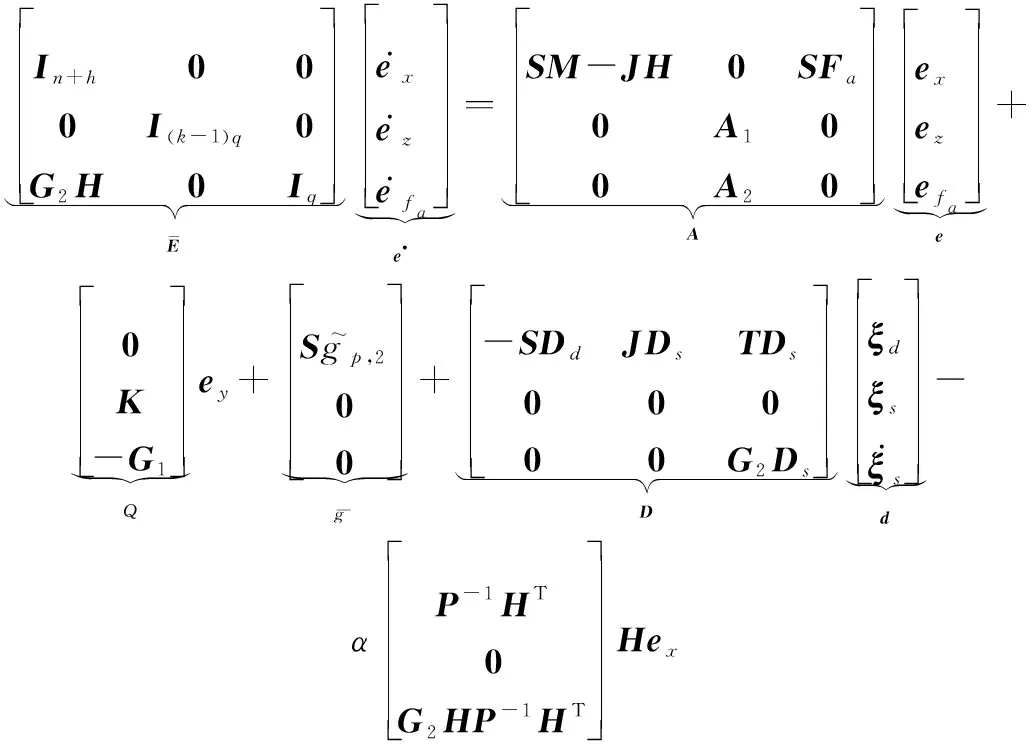
(14)

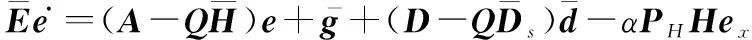
(15)

其中,

=[(),, ()]

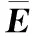
(16)

其中,

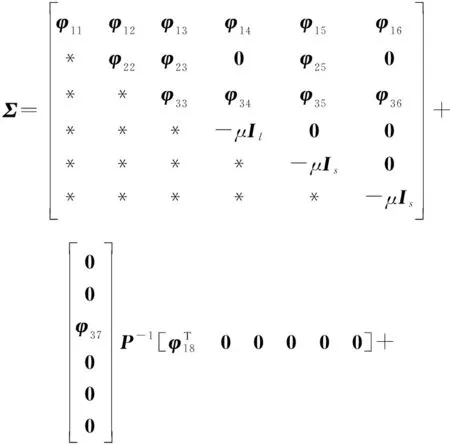
针对满足假设1～假设4的非线性系统,设计FAUIO,如果存在对称正定矩阵和矩阵,,和以及干扰抑制参数使得如下的LMI优化问题存在可行解:

min

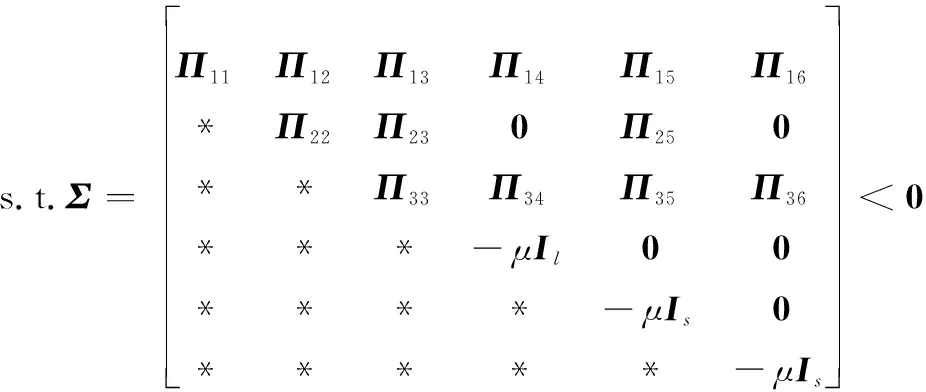
(17)

定义Lyapunov函数为

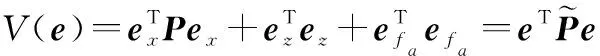
(18)

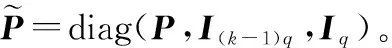
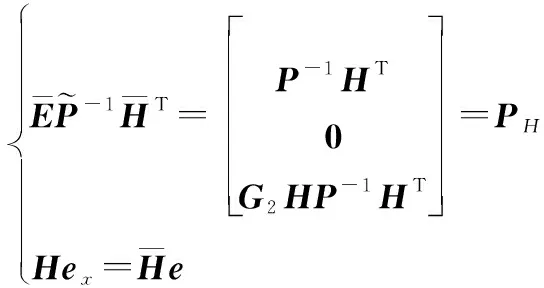
(19)

因此,估计误差动态系统可表示为

(20)

进一步对()沿着误差动态系统求导可得

(21)

因为,2(,)是Lipschitz非线性项,因此有

(22)

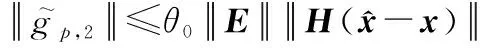
(23)

应用不等式+≤+2,可以得到:

(24)

如果式(8)中的参数满足:

(25)

有

(26)

则式(24)可进一步变为

(27)

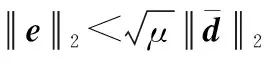
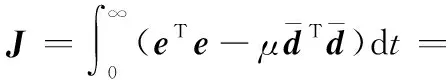
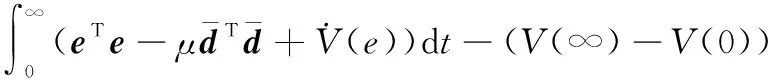
(28)

假设(0)=,因此有:

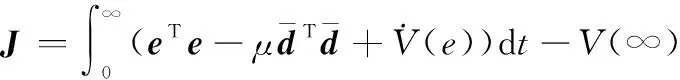
(29)

又因为(∞)>0成立,则可以求得

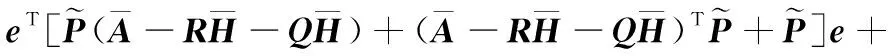
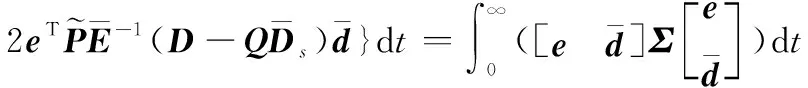
(30)

其中

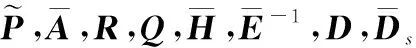
证毕

因为式(17)存在非线性项,属于非线性矩阵不等式,不便于求解,因此需要将其转化为线性矩阵不等式(linear matrix inequality, LMI),然后应用Matlab的LMI工具箱进行求解。因此,给出如下引理和定理用于求解LMI优化问题。

给定矩阵=,以及适维矩阵,和,则

++<

(31)

对任意满足≤的成立的充分必要条件为存在常数>0,使得

+ε+<

(32)

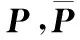
min

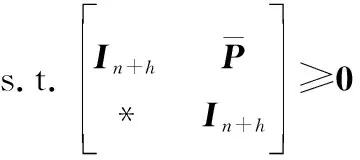
(33)

(34)

(35)

令=,则式(17)可重新表示为

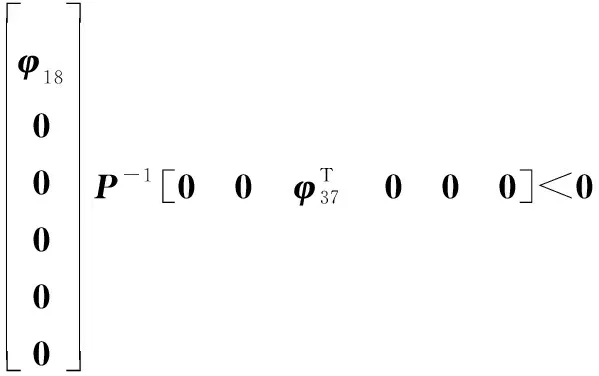
(36)

令正定矩阵满足≤+。因此,利用引理1可以得到一个标量>0,使不等式满足

(37)

根据Schur补定理,式(37)等价于式(38),≤+等价于式(39)。

(38)

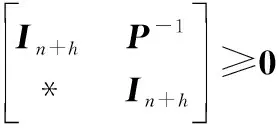
(39)

进一步令=[()],则式(38)可重新表示为

(40)

证毕

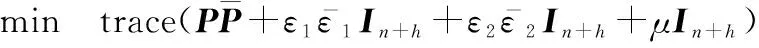
s.t. 式(33)、式(34)以及

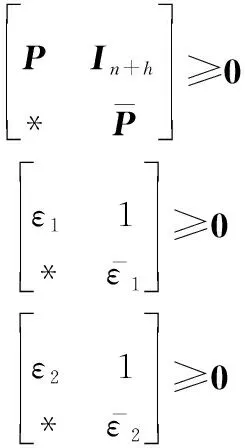
(41)

式(41)的求解过程可参考文献[17],这里不再赘述。

3 多故障重构

若由式(41)所描述的优化问题有解,则可以通过式(1)同时完成非线性系统中执行器故障和传感器故障的重构,即非线性系统的多故障重构任务。

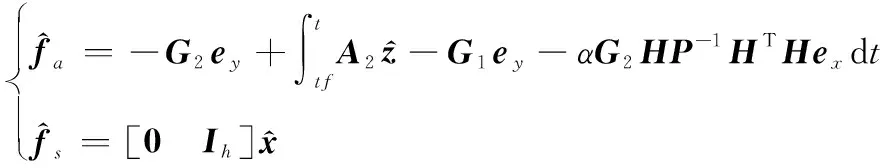
(42)

下面给出观测器进行多故障重构的具体流程:

首先将原始系统构造成如式(7)所示的增广系统;

应用式(10)求解得到观测器增益矩阵和;

使用文献[17]设计的优化迭代算法解算式(41)描述的优化问题,从而得到观测器增益矩阵,,和=;

根据式(9)计算求得其他观测器增益矩阵和;

最后应用所求得的FAUIO在式(42)的引导下重构执行器故障和传感器故障。

4 算例仿真

为进一步验证本文所提出的基于FAUIO的非线性系统多故障重构算法的有效性与可行性,以文献[13]给出的单关节柔性机器人算例进行仿真分析,其非线性动力学方程表示为

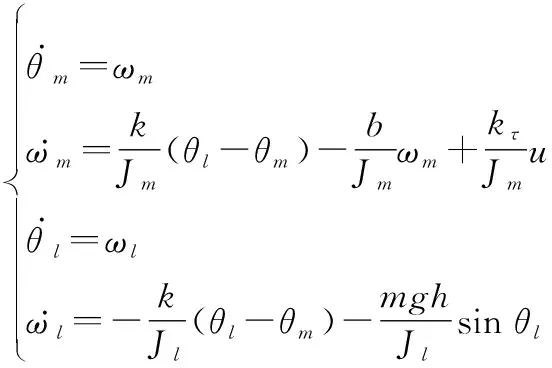
(43)

式中:,,和分别表示电机位置、电机速度、连杆位置和连杆速度。

式(43)的相关参数定义见文献[20]。与此同时,定义系统状态向量为=[,,,]。因此,可以得到系统的矩阵分别为

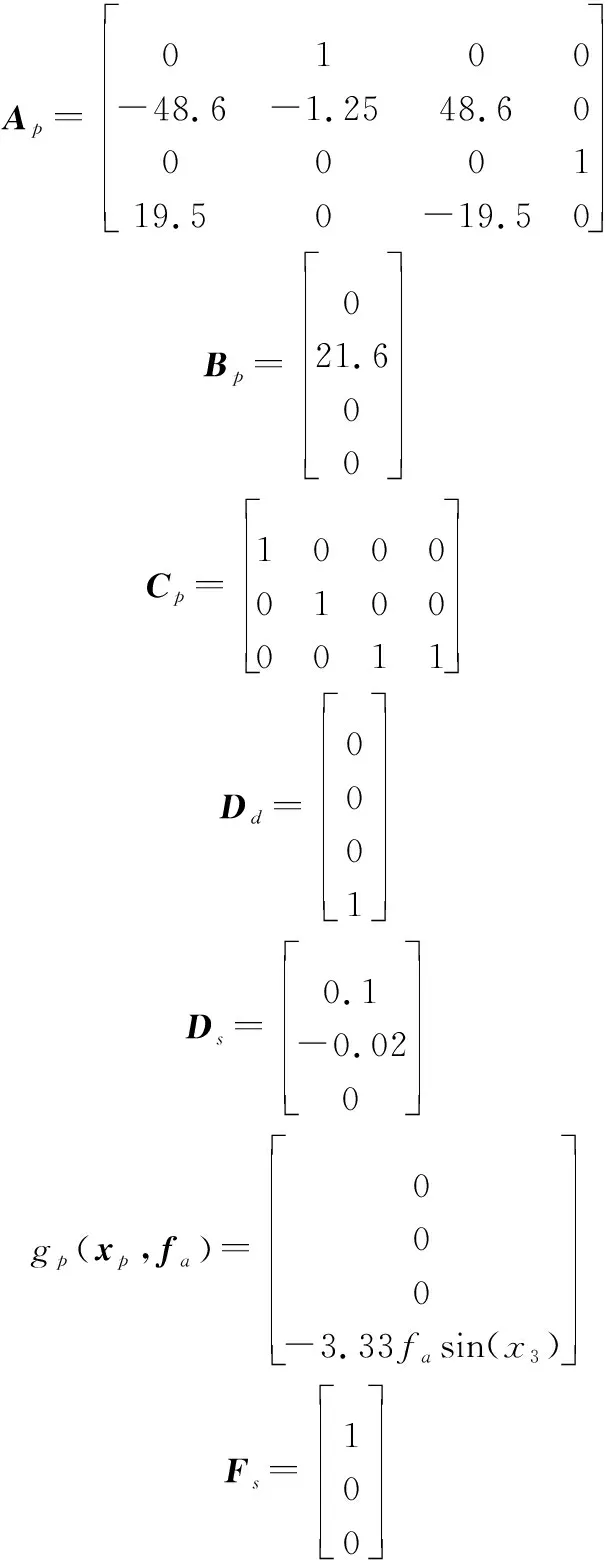
系统的未知输入干扰及测量噪声干扰分别定义为=02sin(10)和=01sin(10)。

与此同时,系统的控制输入和状态向量的初始值分别为=2sin(2π)和(0)=[0, 0, 0, 0]。观测器的初始状态也都为0。

最后给出系统的传感器故障(渐进故障)和多项式形式的执行器故障(渐进故障):

=01(-3)·(-3)-01(-8)·(-8)

式中:()为Heaviside单位阶跃函数。

首先根据式(10)求得观测器增益矩阵和为

接着应用LMI工具箱求解由式(41)描述的非线性优化问题,得到观测器的相关设计参数分别为

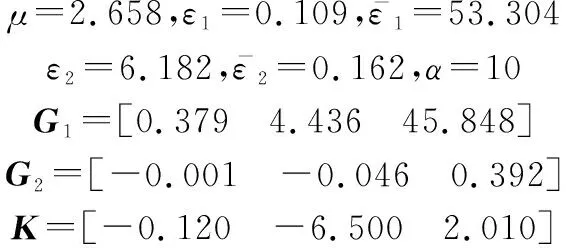
考虑到空间的限制,这里只给出系统部分状态向量和其重构值曲线,如图1和图2所示,图3和图4表示系统执行器故障的重构值和重构误差值曲线,图5和图6表示系统传感器的重构值和重构误差值曲线。从图1和图2可以看出本文提出的FAUIO能够迅速跟踪系统的状态且跟踪精度较高。从图3～图6可以看出,本文提出的基于FAUIO的多故障重构策略可以同时重构系统执行器故障(耦合于非线性函数中)和传感器故障,且重构精度和鲁棒性能都符合预期的设计要求。

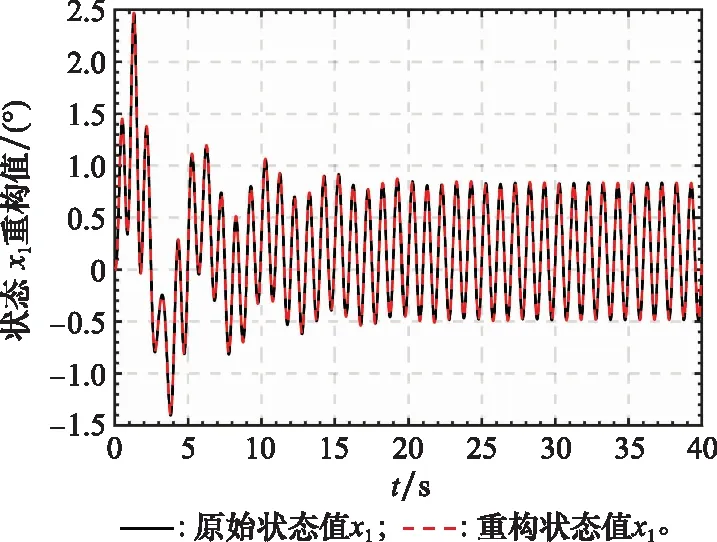
图1 系统状态x1和x1的重构值Fig.1 System state x1and its estimated value

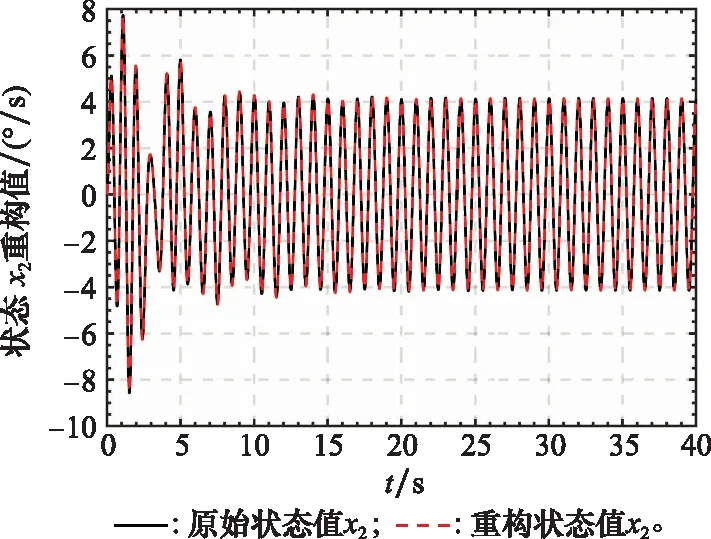
图2 系统状态x2和x2的重构值Fig.2 System state x2 and its estimated value

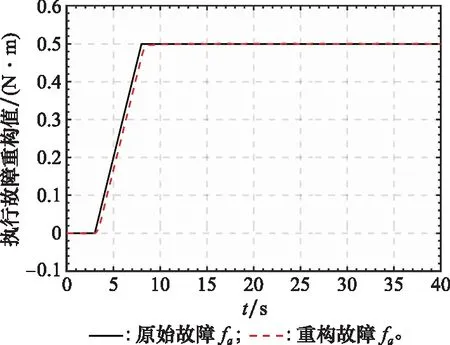
图3 执行器故障fa和fa的重构值Fig.3 Acurater fault fa and its estimated value

图4 执行器故障fa的重构误差值Fig.4 Acurator fault fa estimation error

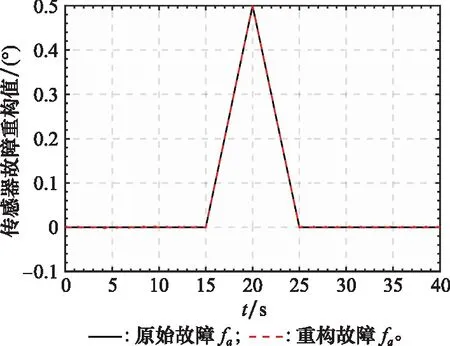
图5 传感器故障fs和fs的重构值Fig.5 Sensor fault fs and its estimated value

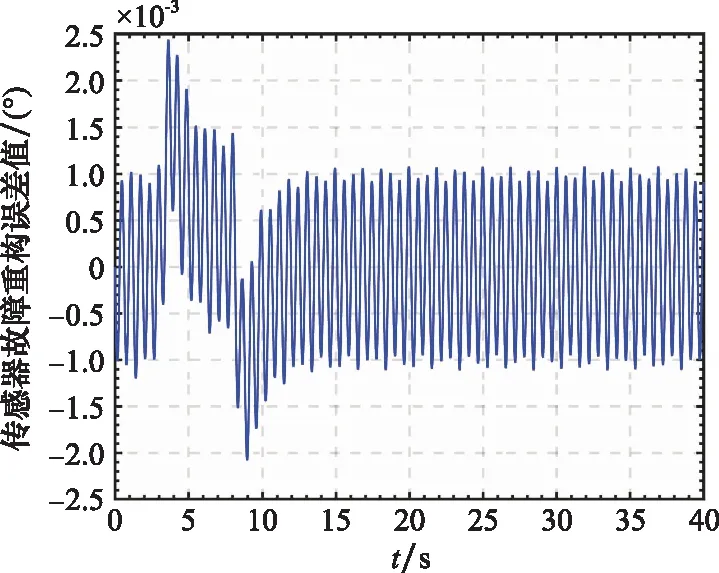
图6 传感器故障fs的重构误差值Fig.6 Sensor fault fs estimation error

为了进一步说明本文所提出FAUIO的优越性能,将其与文献[18]中提出的传统自适应观测器,即AO和文献[23]中提出的自适应未知输入观测器,即AUIO进行了比较。同样,考虑到空间的限制以及传统AO不能用于估计系统传感器故障,这里只给出执行器故障重构结果的对比分析,如图7和图8所示。此外,为了定量地分析仿真结果,采用故障估计误差的均方根值(root mean square of the estimation error, RMSE)来评估不同观测器估计不同类型故障时的准确性,如表1所示。同时,采用稳定时间,即估计误差收敛至稳定态时所花费的时间,以此来评估不同观测器估计不同类型故障时的快速性,如表2所示。

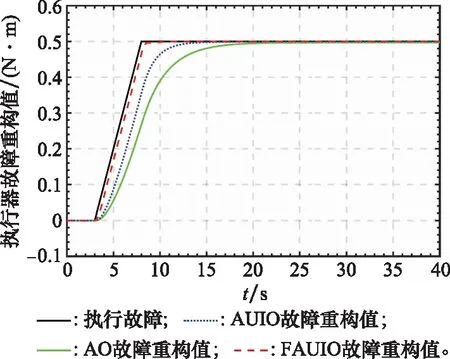
图7 执行器故障fa重构对比结果(渐进故障)Fig.7 Comparison of actuator fault faestimation results (a ramp-type fault)

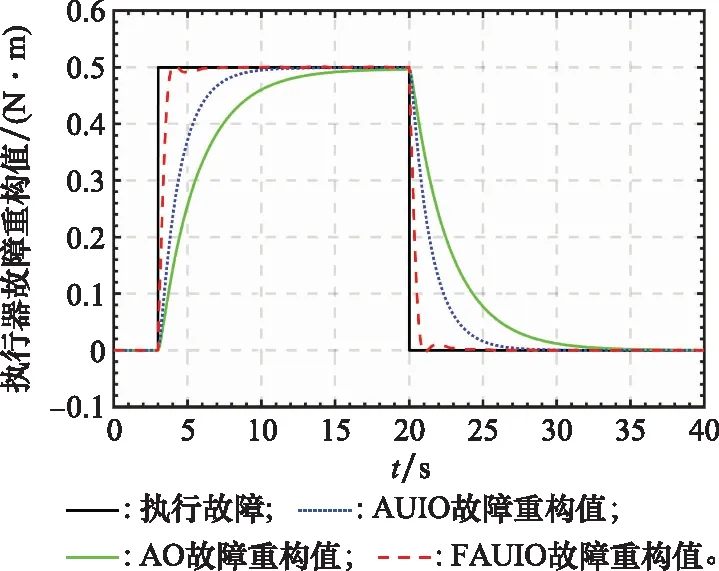
图8 执行器故障fa重构对比结果(突变故障)Fig.8 Comparison of actuator fault fa estimation results (a pulse-type fault)

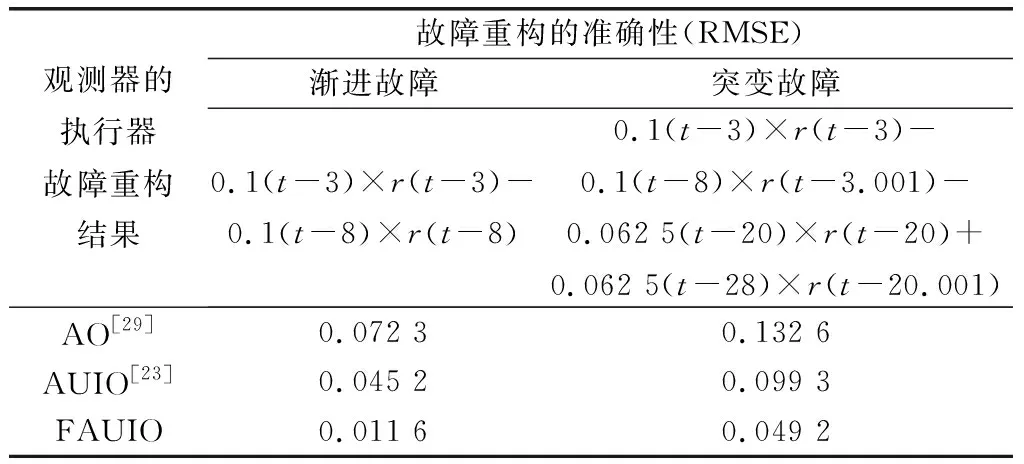
表1 观测器重构不同类型故障时的RMSE指标

表2 观测器重构不同类型故障时的稳定时间ts指标

由上述仿真结果可以看出,不论是在定性评估方面(见图7和图8所示结果),还是在定量评估方面(见表1和表2所示结果),本文提出的FAUIO重构不同类型故障时的准确性和快速性都优于传统的AO和AUIO。因此,本文提出的FAUIO的故障重构性能得到了充分验证。

5 结 论

本文提出了一种基于AUIO的非线性系统多故障重构策略,实现了系统中执行器故障和传感器故障的同时重构。利用性能指标同时削弱了未知输入干扰和测量噪声对重构结果的影响。通过引入比例项提高了故障重构的快速性。与已有方法相比,本文创新性地考虑了一类非线性函数中耦合执行器故障的非线性系统,设计执行器故障解耦方法并成功实现了故障重构。最后,将本文提出的FAUIO应用于单关节柔性机器人系统,仿真算例结果验证了所提方法的有效性。

将本文提出的FAUIO拓展到更复杂的系统中,如T-S模糊非线性系统、马尔可夫跳跃系统和时滞系统,以及在考虑系统的稳定性、鲁棒性、可靠性和控制性能的同时,将FAUIO的故障估计结果应用于不确定非线性系统的容错问题研究将是下一步重点研究的内容。