基于滞后效应函数的土石坝渗流统计模型分析

余正源，黄耀英，费大伟，丁 倩，包腾飞

（1.三峡大学水利与环境学院，湖北 宜昌 443002；2.安徽绩溪抽水蓄能有限公司，安徽 绩溪 245300；3.河海大学水利水电学院，南京 210024）

0 引 言

土石坝竣工蓄水后，其渗流性态是大坝安全的重要因素之一［1］。为此，建立合理的土石坝渗流统计模型，准确分析并监控土石坝内部的渗流性态，保证监测人员对大坝安全做出合理的判断具有重要意义［2］。渗流监测资料和理论分析表明，由于非稳定渗流场的影响库水位和降雨对大坝渗流的影响存在滞后效应［3］。所以在建立统计模型分析土石坝渗流状态时，首先需要解决如何模拟库水位及降雨的滞后作用。以库水位为例，目前反映其滞后效应的方法主要包括前期平均法［4-6］和等效库水位法。前期平均法主要存在选取时间粗糙，不能合理反应库水位影响累积滞后效应等问题［7］。为此，郑东健［8］提出了静态永久滞后效应函数法和动态效应函数法，即采用等效水位的思想，用正态分布模拟库水位的作用过程。其中考虑库水位动态效应权重的等效库水位计算方法，可以更好的描述变化库水位下的大坝渗流场，在大坝工程中的坝基扬压力水头［9］、渗流量［10-12］、测压管水位［13］等方面的应用中验证了该方法的实用价值及有效性。然而在该方法的实际工程应用中，重点关注的是采用更好的智能算法来识别参数使模型拟合效果更好，少有对滞后累积效应进行分析，而滞后效应的规律与大坝渗流性态有着密切联系。因此，本文基于实际工程近20年的渗流监测资料，建立考虑滞后效应的测压管水位统计模型，与传统统计模型对比展示了其有效性并进一步分析了滞后效应的规律。

1 基于滞后效应函数的土石坝测压管水位统计模型

1.1 土石坝测压管水位统计模型

土石坝测压管水位主要受上下游水位、降雨和时效的影响，有时也受温度的影响，由此建立测压管水位统计模型为

式中：H为测压管水位；Hu为上游水位分量；Hd为下游水位分量；HP为降雨分量；HT为温度分量；Hθ为时效分量。

（1）库水位分量。现有报导的库水位分量采用的平均库水位的概念比较模糊，事实上库水位对测压管水位的作用并不是一个平均的过程，其可能当天达到最大效应，也可能3～5d甚至更晚才达到，该过程存在滞后累积效应，且库水位对渗流的影响效果是先逐渐上升然后逐渐下降的过程。因此，假设库水位对渗流变化影响服从正态分布，引入滞后效应函数表示库水位分量为［14］：

式中：Hu为库水位分量；a1为库水位分量的回归系数；x1为库水位对测压管水位影响的滞后天数；x2为库水位正态分布标准差，即库水位对测压管水位影响天数；hud为等效库水位；hu（t）为t时刻的库水位；x1和x2需要优化计算求得，本文采用粒子群算法辨识库水位滞后天数和影响天数。对于大坝环境量监测数据，库水位一般每天一个测值，为此在计算库水位分量时，需要把连续型积分转化成离散型积分，根据统计学原理积分区间取x2的2～3倍即可满足计算要求。

（2）降雨分量。由降雨监测资料分析可知，降雨对测压管水位的作用同库水位相似，也是逐渐达到最大效应之后逐渐减弱。为了反映降雨对渗流的实际影响情况，引入降雨滞后效应函数的概念。采用与库水位分量同样的滞后模式，即与式（2）类似［15］：

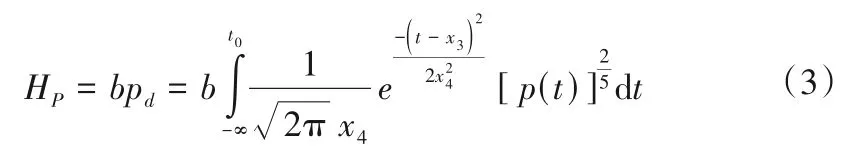
式中：HP为降雨分量；b为降雨分量的回归系数；x3为降雨对测压管水位影响的滞后天数；x4为降雨影响权正态分布标准差，即降雨对测压管水位影响天数；p(t)为t时刻的降雨量；pd为等效降雨量。x3、x4同样由粒子群算法优化辨识得到。

（3）其他分量。下游水位通常对渗流影响很小，一般采用当日下游水位作为因子；当土石坝测压管水位受温度影响时，一般用谐波函数的形式作为因子；时效分量比较复杂，与坝前泥沙淤积和地基固结等有密切联系，一般采用一次项与对数项的组合形式。

综上所述，考虑滞后效应函数的测压管水位统计模型为：

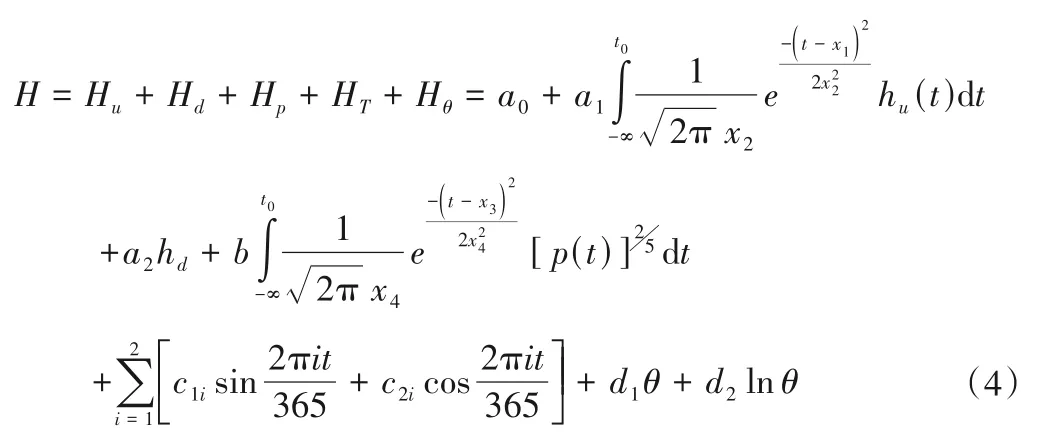
式中：a0为常数项；a2、c1i、c2i、d1、d2为回归系数；t为观测日至模型首次观测日的累计天数；θ=；其他参数同前。

我们对哲学的理解，本来就有一种近科学的解释:把哲学看作科学，或者说是科学的一部分。于是，在广义科学的概念中，就包含了哲学。马克思主义哲学作为现代哲学，同科学具有非常多的相似性，甚至可以说就是同类。如果哲学是一种科学，那么它运用假说方法，就是顺理成章的事情。如果我们强调哲学与科学的区别，甚至认为哲学和科学完全不同，那么在实证科学中通用的假说方法，在哲学中就可能用不上了。所以到底哲学中是否允许假说，这也是个问题。为了回答这个疑问，我曾写过题为《哲学研究中的假说方法》的论文，1988年发表在《现代哲学》上。

1.2 基于粒子群算法优化测压管水位统计模型

模型求解重点是确定滞后参数，即寻找最优参数使统计模型复相关系数最大。在众多算法中，粒子群优化算法结构简单、实现方便且运行速度快，能以较大概率收敛于全局最优解，所以本文采用粒子群算法［16］来搜寻滞后参数。即首先引入滞后效应函数来建立新的统计模型，然后基于测压管实测数据，通过粒子群算法搜索库水位和降雨的滞后天数以及影响天数，最后采用逐步回归算法优化模型各个分量的系数。模型建立基本流程图见图1。

图1 测压管水位统计模型优化流程图Fig.1 Flow chart of optimization of statistical model for piezometric level

2 工程实例

2.1 工程概况

王甫洲水利枢纽左右岸围堤土石坝是采用土工膜作为防渗体的砂砾石坝。本文选取位于右岸围堤土石坝中间的GY5断面渗流监测断面进行分析，该监测断面共布置6根测压管，分别为GY5-1、GY5-2、GY5-3（废孔）、GY5-4、GY5-5 和GY5-6，布置图见图2，监测数据较完整。

图2 GY5断面测压管布置图Fig.2 GY5 section piezometer tube layout

2.2 复合土工膜土石坝坝体渗流性态定性分析

该工程下闸蓄水以来的库水位、降雨和测压管水位过程线如图3和图4。由图可知：①各支测压管在运行期呈现出相同的变化规律，变化都比较平稳，从监测断面上来看，从上游到下游测压管水位呈现出递减的趋势［17］。但GY5-2 相较于其他测压管，在蓄水初期和2006年出现了较大的水位波动。②由过程线对比可以看出，库水位变化与测压管水位变化的相关性不明显，较难确定其影响测压管水位的滞后时间；在降雨集中的时间段内，测压管水位虽有所上升，然而由于降雨时空分布的不规律性，也较难确定其影响的滞后时间，同时由于GY5-2 存在较大的水位波动，此时采用传统统计模型拟合的效果往往不太理想，因此采用本文提出的统计模型来定量分析库水位、降雨及其他因素对测压管水位的影响。

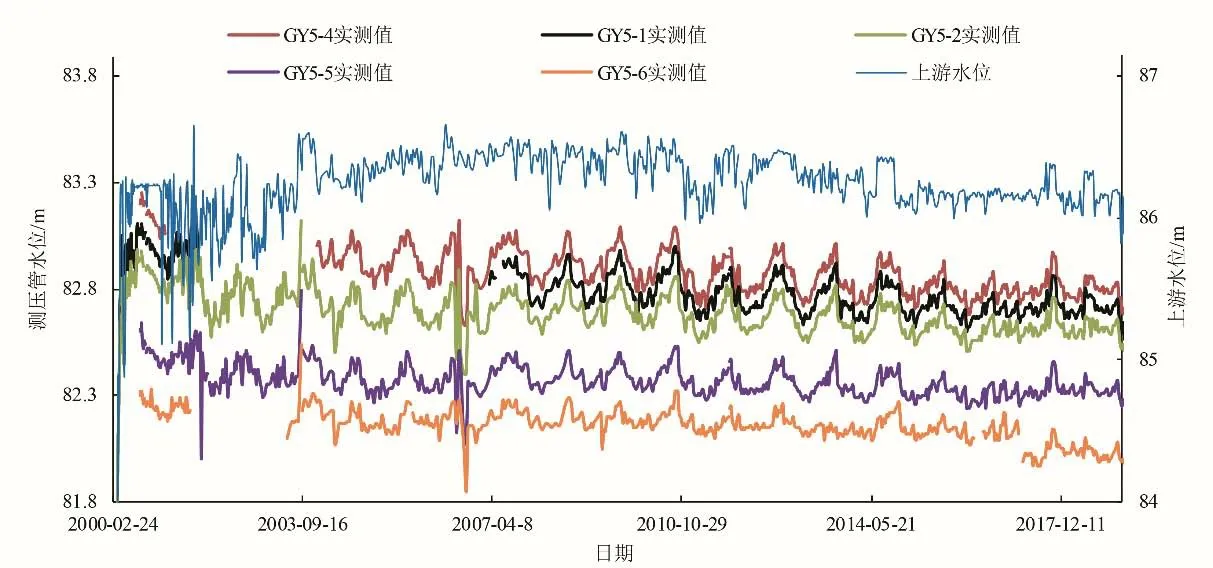
图3 库水位和测压管水位过程线Fig.3 Process line of reservoir water level and piezometric level

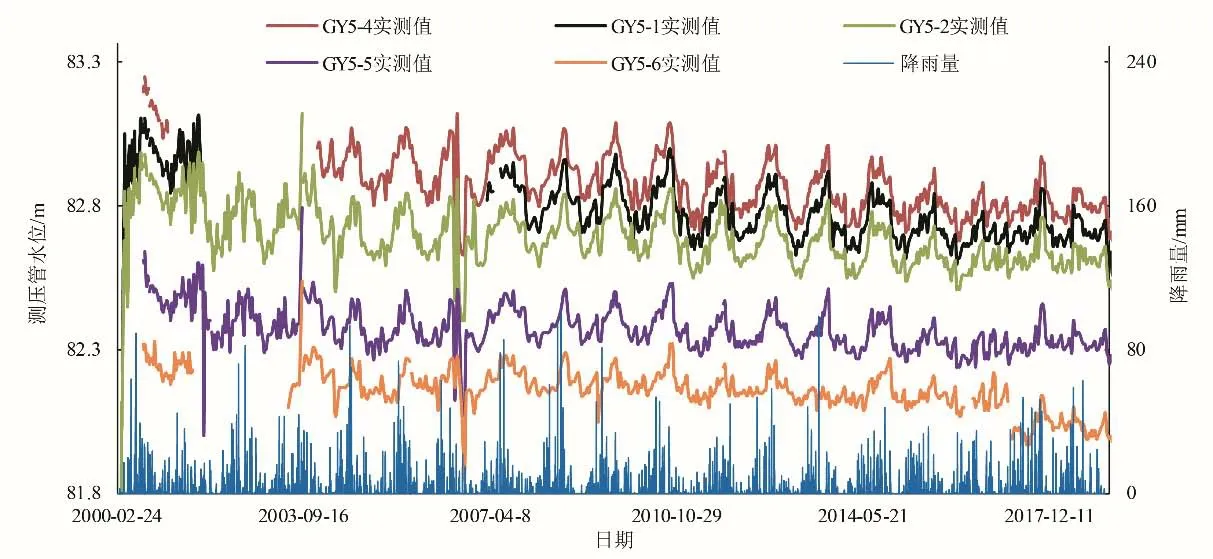
图4 降雨和测压管水位过程线Fig.4 Process line of rainfall and piezometric level

2.3 考虑滞后函数的测压管水位统计模型分析

在建立统计模型［式（4）］时，由于GY5-1、GY5-2、GY5-4测压管基本分布于坝体中部，距下游排水沟较远，因此建立统计模型时不考虑排水沟水位的影响，而对于GY5-5、GY5-6 两支测压管，由于离下游排水沟很近，受其影响较大，在建立统计模型时考虑了下游排水沟水位的影响。此外GY5 监测断面围堤的体型不大，当上游水位长时间稳定在正常蓄水位左右时，围堤上游坡面大部分处在水面以上，所以环境气温等因素对坝体渗流存在一定的影响。因此，增加谐波函数来描述周期性变化的环境因素对测压管水位的影响［18］。

2.3.1 库水位滞后天数分析

在建立新的统计模型后，结合原型监测资料采用粒子群算法辨识模型的滞后参数，本次识别滞后参数的粒子群算法程序为MATLAB 工具箱PSOt。进行库水位、降雨滞后参数优化查找时，种群规模数N设置为24，搜索区间设置为［0，60］，每一次搜寻计算各粒子的适应度并进行适应度评价，然后更新各粒子的速度以及位置，直到收敛精度达到1e-25终止算法。

（1）库水位滞后天数空间分布分析。图5为各参数空间分布图，图中x1、x2、x3和x4分别为库水位滞后天数、库水位影响天数、降雨滞后天数和降雨影响天数。从图中可以看出：库水位滞后天数整体较大，并且随着测压管离上游库水位的距离越远，库水位影响的滞后天数逐渐增大，符合土石坝渗流基本规律，模型计算结果较好。

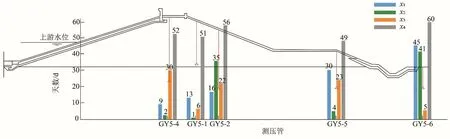
图5 滞后参数空间分布Fig.5 Spatial distribution of hysteresis parameters

（2）库水位滞后天数时变效应分析。为了研究库水位影响滞后天数的时变效应，本文以数据完整性较好的测压管GY5-2为例，将监测系列分成6个时间段，分别采用粒子群算法辨识库水位及降雨的滞后天数和影响天数，计算结果如表1所示。

表1 GY5-2各时间段库水位及降雨的滞后天数和影响天数的计算结果 dTab.1 Calculated results of the hysteresis days and affected days of the reservoir water level and rainfall in each period of GY5-2

由表可知：①在近20年运行期间，库水位滞后时间变化较稳定，在水库运行初期，库水位滞后时间有所增大，其原因可能与坝前泥沙淤积以及土体固结导致渗透系数减小有关，之后多年库水位滞后时间波动不大，基本稳定在16 d；②影响库水位滞后时间的主要因素有介质的物理性质（渗透系数）、给水度和测压管的管径大小等，测压管的管径一般变化不大，所以在稳定渗流场中，滞后时间的变化可以一定程度上反映土石坝防渗体渗透系数的变化情况。从滞后天数的时变效应可以看出该处土石坝防渗体在多年运行中，渗透系数变化不大，即复合土工膜在多年服役中防渗效果依然保持良好。

2.3.2 考虑滞后效应函数的测压管水位统计模型各分量分析

粒子群算法辨识出滞后参数后，用逐步回归求解模型系数，最终所建立的测压管水位统计模型的复相关系数R 均达到了0.85 以上，拟合效果较好，能够定量反映出GY5 断面的渗流特性。表2为运行期测压管水位分量最大变幅统计。由计算结果可知：水库进入运行期后，库水位稳定在正常蓄水位（86.23 m）附近，库水位变化较小，对应的围堤土石坝内部测压管水位受库水位变化影响也较小，从表2可以看出，GY5断面各支测压管水位的库水位分量最大变幅基本在0.12 m 左右。此外各支测压管水位受降雨和温度影响也较小，降雨和温度分量最大变幅基本在0.1 m左右。

表2 运行期测压管水位分量最大变幅统计 mTab.2 Statistics of maximum variation of water level component of piezometric during operation

2.3.3 与传统统计模型对比分析

为进一步探讨该方法的有效性，同时采用传统的土石坝测压管水位统计模型对这5 支测压管监测数据进行拟合，模型表达式如下：

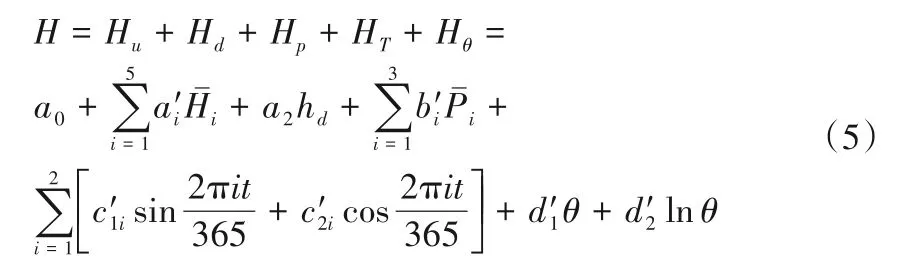
式中：a′i为库水位分量回归系数，Hˉi为观测日当天、前1 d、前2 d、前3 d、前4～7 d 的平均上游库水位（i=1～5）；b′i为降雨分量的回归系数，Pˉi为观测日当天、前1 d、前2 d 的平均降雨量（i=1～3）；其他参数同前。

采用逐步回归法对传统统计模型系数进行求解后，与考虑滞后效应函数的统计模型进行对比，模型的复相关系数统计如表3所示，图6为GY5-2 两种模型拟合效果对比图。由图表可知，相比于传统的统计模型，考虑滞后效应函数的统计模型拟合效果均有所提高，GY5-1、GY5-4、GY5-5和GY5-6复相关系数提高了0.002～0.012，而GY5-2的复相关系数提高了0.147，其原因为考虑滞后效应函数的渗流统计模型更好地反映了GY5-2数据波动较大的规律。

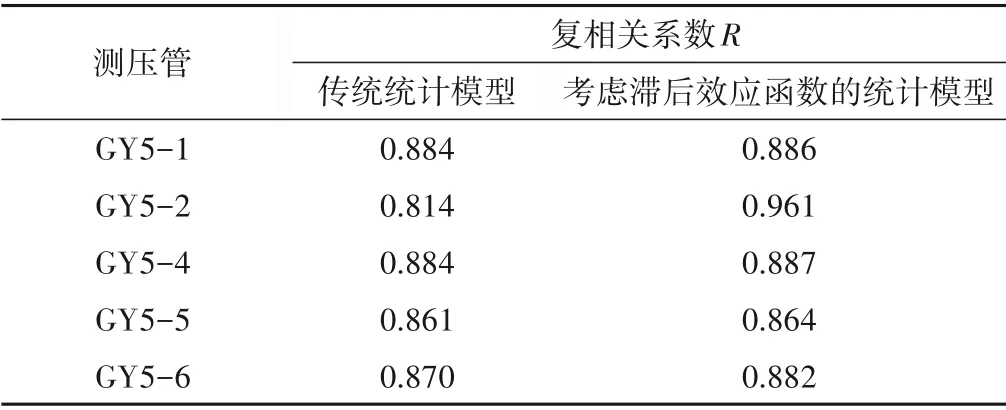
表3 复相关系数统计Tab.3 Multiple correlation coefficient statistics

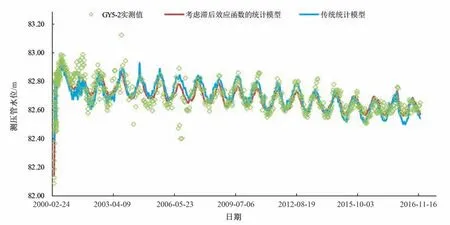
图6 GY5-2两种模型拟合效果对比Fig.6 GY5-2 Comparison of fitting effects between the two models

3 结 论

对于土石坝工程，库水位及降雨对坝体测压管水位的影响不能简单看作一个“平均”过程，本文引入滞后效应函数来反映其作用过程，并采用粒子群算法对影响天数及滞后天数进行智能寻优建立了考虑滞后效应的统计模型，在实际工程应用中，与传统统计模型对比展示了模型的效果，并进一步分析了滞后效应的规律。结果表明：

（1）随着离上游迎水面距离越远库水位影响滞后天数越大，符合土石坝渗流基本规律，模型计算结果较好；由GY5-2库水位影响滞后时间多年保持稳定，可以看出GY5断面复合土工膜工作性态保持良好；与传统统计模型对比分析表明，当测压管水位波动较大时，采用本文提出的统计模型拟合效果更好。

（2）土石坝竣工蓄水后，坝内渗流场由非稳定状态逐渐趋于稳定状态，其渗流性态是大坝安全的重要因素之一。引入滞后效应函数建立的统计模型可以更加准确合理的反应库水位和降雨的作用过程，同时分析库水位滞后效应的分布特征及变化规律不仅可以一定程度反映土石坝渗流场的变化情况，也可为今后分析评价大坝防渗体的工作性态提供一项参考指标。