基于Morris、Sobol和EFAST的LID设施模型参数全局敏感性分析

金梦潇，田 勇，Michele Lancia，于 江，郑春苗

（1.哈尔滨工业大学环境学院，哈尔滨 150090；2.南方科技大学环境科学与工程学院地表水-地下水污染综合治理国家环境保护重点实验室，广东 深圳 518055；3.北京大学工学院水科学中心，北京 100871）

0 引 言

不断加快的城市化进程增加了不透水面的覆盖率，影响了自然水文循环过程，进而威胁到城市水生态环境。我国在2014年首次提出“海绵城市”的管理理念来解决城市化导致的一系列水环境问题［1，2］。海绵城市的建设重点是结合低影响开发（Low Impact Development，LID）的理念［3］，通过分散的、源头的设施使雨水就地下渗，控制径流量等，来达到调蓄雨水的目的。LID设施包括雨水花园、透水铺装、生物滞留池、植被草沟、下沉绿地等，不同的LID设施对增加雨水下渗、控制径流总量和削减径流峰值有着不同的效能。为了评估各类LID 设施的效能，可利用SWMM 构建包含LID 设施的水文模型，模拟LID 设施的水文过程及控制效果，这是海绵城市规划设计中不可或缺的重要环节。

在海绵城市规划设计中，LID 设施模型的参数众多。识别参数的敏感性，对筛选LID 设施及筛选后进行的SWMM 模拟计算和结果分析具有重要意义。敏感性分析是从众多输入参数中识别对输出结果有显著影响参数的方法，对提高模型应用效率有重要帮助［4］。敏感性分析方法众多，大致可分为局部敏感性分析和全局敏感性分析两大类。局部敏感性分析［5］是研究在局部范围内，单个输入变量（其他变量保持不变）变化对输出结果的影响，常用方法包括OAT 法、DA 法。局部敏感性分析原理简单、计算量小，但不能充分描述模型参数的空间分布形态，忽略了参数之间的相互作用。全局敏感性分析［6］是研究多个输入变量同时变化对模型输入结果的影响，此种方法把输入变量的变化范围扩展到多个参数的定义域，可得到不同参数之间的相互作用，常用方法包括Morris 法、Sobol 法、EFAST 法等［7］。由于LID 设施模拟涉及复杂的非线性水文过程，因此本研究选用三种全局敏感性分析方法对LID 设施的各参数进行对比研究，为提高模型优化及LID设施效能提供技术支撑。

1 研究方法

1.1 SWMM模型

SWMM（Storm Water Management Model）是由美国环境保护署（Environmental Protection Agency，EPA）开发的一款可以进行城市雨洪管理的分布式水文模型。此模型一般多应用于模拟城市某一单一或长期降雨事件的地表径流水量和水质变化［8］，近年来有很多研究将SWMM 模型应用于海绵城市的规划和设计［9，10］，以及分析和评估LID 设施对不同频率城市雨洪的径流控制效果［11-13］。

1.1.1 SWMM 模型构建

研究区域位于深圳市宝安区新桥河流域，流域总面积约为34.67 km2，地势东南高、西北低，雨水从东南向西北汇集，最后通过管道流入新桥河。该区域土地利用主要以居住用地和工业用地为主，不透水面面积较大，约占总面积的67%；而以林地为主的透水面面积则占总面积的33%。流域内有1个气象观测站。图1为研究区域的SWMM 概化图。依据实际的勘察资料，将研究区域划分为92 个子汇水区，112 个雨水收集管道。基于收集的90 m分辨率数字高程地图和土地利用类型，使用ArcGIS软件计算每个子汇水区的面积、坡度、不透水比例和排水管道长度等参数，作为SWMM模型的输入。

图1 研究区域SWMM概化图Fig.1 SWMM model of the study area

模拟采用长期降雨事件。降雨数据为深圳市气象局提供的万丰站日降雨量数据，监测日期为2018.01.16-2018.10.16（9个月），总降雨量为1 779 mm。

1.1.2 SWMM 模型校正

根据实地勘测资料和SWMM 手册里的参数参考范围，确定模型参数的初始数值，对不透水面和透水面的曼宁系数（N-Imperv、N-Perv）和洼地蓄水（Dstore-Imperv、Dstore-Perv），以及Horton 下渗公式的相关参数进行调参。分别选取2018.04.04-2018.04.23（20 d）和2018.06.04—2018.06.23（20 d）进行模拟，通过监测点河水水位的模拟值和监测值的对比进行调参。最终模拟结果如图2所示，模拟值和监测值的河水水位基本相同，波动情况基本相似。

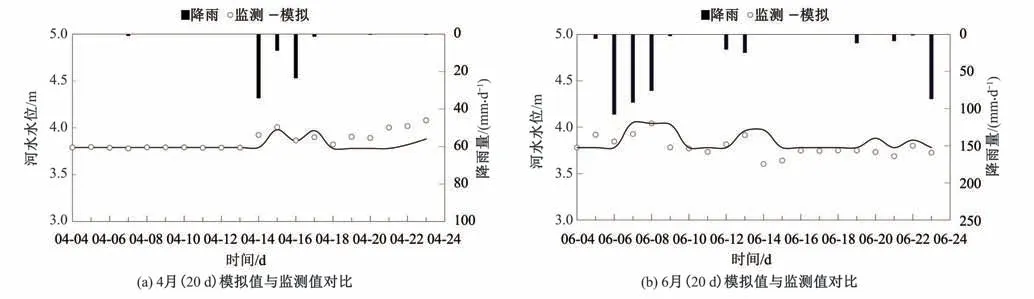
图2 模拟值和监测值对比Fig.2 Comparison of simulated and monitored values

1.1.3 LID设施模型参数

本研究在新桥河流域现状条件基础上开展了海绵城市设计（图3），在校正后的SWMM 上加入相应的LID 设施模型，来模拟海绵城市水文过程并进行参数敏感性分析。LID 设施模型是SWMM 里的一个模块［10］，此模块可以模拟不同类型LID 设施在暴雨情景下的蓄滞、蒸发、下渗及排水过程。在SWMM 里，将LID 设施垂直方向概化成地表层、土壤层、蓄水层及相关排水系统，不同的LID 设施进行不同层的组合［14］。本研究主要选择了4 种LID 设施：植被草沟（下沉绿地）、绿色屋顶、生物滞留池（雨水花园）和透水铺装。根据各汇水区的土地功能及LID 设施的地形需求，通过海绵城市规划设计的方法，将4 种LID 设施分配设置在每个子汇水区。规划完成后每种LID设施的面积及在该区域海绵城市设计面积中的占比分别为，植被草沟2.472 km2（37.9%）；绿色屋顶2.436 km2（37.2%）；生物滞留池1.178 km2（18.0%）；透水铺装0.451 km2（6.9%）。

图3 研究区域的海绵城市设计图Fig.3 Design of sponge city in the study area

4 种LID 设施的部分模型参数采用设计值，例如土壤地表层下凹深度、地表坡度等。本次研究选择地表层和土壤层的模型参数进行敏感性分析（而其设计值参数不予考虑）。根据筛选结果，确定4 种LID 设施的25 个参数（表1）。各参数的取值范围参考SWMM 手册，其中SWMM 规定土壤的孔隙率应大于田间持水量，田间持水量应大于凋萎点。

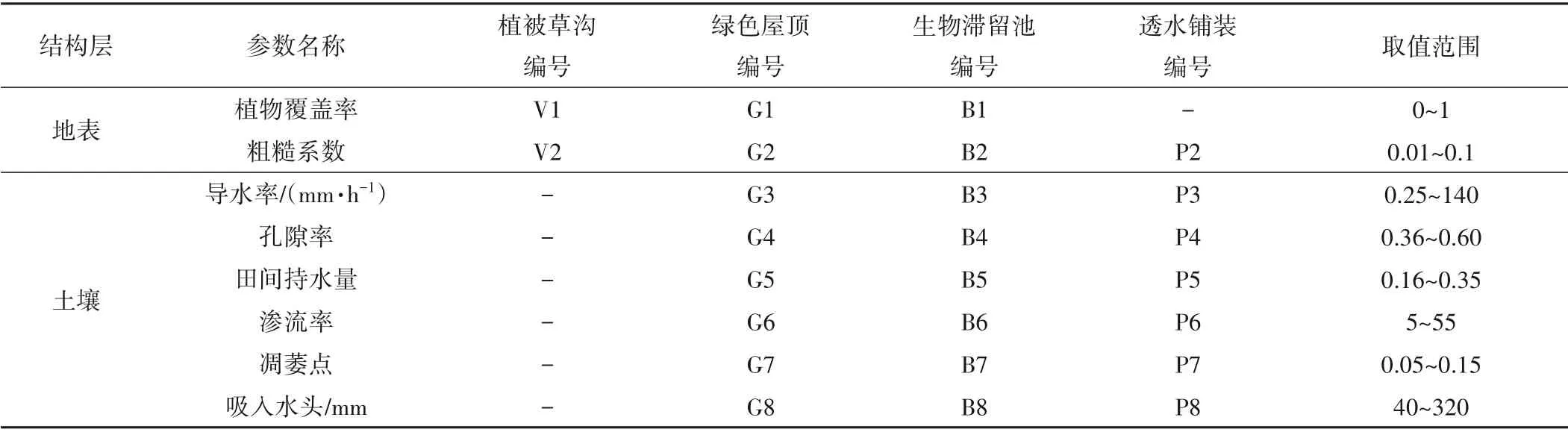
表1 LID设施参数及取值范围Tab.1 Parameters of LID facilities and their value ranges

1.2 敏感性分析方法

全局敏感性分析方法可分为两种，定性分析和定量分析。定性分析是研究不同参数对输出变量响应的相对大小，如Morris 法、Delta Test 法等；而定量分析可获得不同参数对输出变量的贡献率大小，如Sobol 法、EFAST 法等。本研究同时选用Morris、Sobol 和EFAST 三种敏感性分析方法开展研究，分别从定性和定量两个方面揭示SWMM 模型结果对LID 设施参数的敏感性。

1.2.1 Morris法

Morris 法是目前广泛应用的定性全局敏感性分析法［15］，由Max D.Morris 于1991年提出，之后被Campolonge 等［16］改进。Morris 法可以快速筛选出敏感的参数，但无法量化各参数的敏感性。该方法由单独随机的“一次变化法”实验组成，在这些实验中，依次评估改变每个被选择因素的值所产生的影响［17］。

Morris法计算公式为：

式中：Si（X，Δx）为参数i的敏感性指数；y（x）为模型输出结果；X=（x1，x2，…，xn）为参数的n维向量；Δx为x的变化量。

Morris法首先把各参数的取值范围映射到［0，1］之间，构成n维采样空间。在采样空间里，应用一次变化法的试验设计对参数进行随机采样。由于采样方法具有随机性，需进行t次重复，得到更好的采样分布。通过对采样样本进行计算，可得到各参数Si的平均值μ和标准差σ。μ表示输入变量对输出变量影响的强弱，μ值越大则表明输入变量的敏感性越强。σ表示输入变量间相互作用的强弱，σ值越大则表明参数间的相互作用越强。

1.2.2 Sobol法

Sobol 法由Sobol 于1993年提出［18］，其核心是将模型输入的总方差分解成各参数的方差和参数相互作用的方差之和，通过计算各参数对输出方差的贡献比来识别各参数的敏感性［19］。

假设模型为Y=f（X）=f（x1，x2，…，xn），X=［x1，x2，…，xn］是参数向量，n为参数的数量，方差分解公式表示为：

式中：V为模型的总方差；Vi为第i个参数作用的方差项；Vi，j为第i个和第j个参数共同作用的方差项；V1，2，…，n为所有参数共同作用的方差项；Si为第i个参数的敏感性指数。

1.2.3 EFAST法

EFAST（Extended Fourier Amplitude Sensitivity Test）称为扩展傅里叶振幅灵敏度检验法［20］，是在FAST 法的基础上结合Sobol 法改进而来的全局敏感性分析方法。此方法采取了模型方差分析的思想，计算获得模型预测的期望值和方差，来表达各个输入参数间的相互作用［21］。因此，通过模型方差的分解得到各参数间的相互作用对总方差的贡献比，进而得到各参数的敏感性指数。

式中：V为模型的总方差；Vi为第i个参数作用的方差项；Vi，j为第i个和第j个参数共同作用的方差项；Si为第i个参数的敏感性指数。

1.3 敏感性分析过程

采用SimLab2.2软件对LID设施的参数敏感性进行分析（图4），具体过程如下：

图4 敏感性分析的流程图Fig.4 Flow chart for sensitivity analysis

（1）定义LID 设施各参数的取值范围及分布形式。根据SimLab 软件的要求，将表1里各参数的取值范围转换到［0，1］区间内，各参数分布形式均假设为均匀分布。

（2）使用SimLab 软件在多维参数空间内进行随机采集，生成参数样本集。

（3）编写MATLAB 程序，将生成的参数样本集写入对应的SWMM模型文件中，运行模型。

（4）使用MATLAB 程序读取SWMM 模型结果，并将模型结果编写成SimLab 软件可读取的文件格式。通过SimLab 软件的Monte Carlo 方法进行敏感性计算，最终得到各种方法的分析结果。

2 结果与分析

2.1 Morris法分析结果

采用Morris 法对25 个LID 设施模型参数抽样10 次，对得到的260 组样本量进行敏感性分析计算，获得4 种不同输出变量的敏感性指数（μ，σ）散点图（图5）。图5（a）至5（d）分别显示了以蒸发量、雨水下渗、地表径流量和峰值流量为响应变量的敏感性分析结果。

对蒸发［图5（a）］而言，敏感性最高的参数为生物滞留池土壤导水率（B3），其次为植被草沟植物覆盖率（V1）、绿色屋顶导水率（G3）、植被草沟粗糙系数（V2）、绿色屋顶渗流率（G6）；而植被覆盖率（V1）与各输入参数的相互作用最强。雨水下渗［图5（b）］对生物滞留池相关参数的敏感性最高，而对其他LID设施的参数敏感性较低，其中最为敏感及参数相互作用最显著的3个参数均为生物滞留池的导水率（B3）、植物覆盖率（B1）和渗流率（B6）。地表径流量［图5（c）］对生物滞留池导水率（B3）的敏感性最高，其次为透水铺装导水率（P3）和生物滞留池植物覆盖率（B1）。峰值流量［图5（d）］对生物滞留池植物覆盖率（B1）最为敏感，其次为生物滞留池粗糙系数（B2）和绿色屋顶植物覆盖率（G1），参数的敏感性与参数相互作用的排序一致。总之，从4组不同输出变量敏感性分析得出，生物滞留池导水率对模型输出变量的影响较大，其次是生物滞留池的植物覆盖率和粗糙系数。

图5 Morris法敏感性分析结果Fig.5 Sensitivity analysis results of the Morris method

2.2 Sobol法分析结果

选用Sobol 法进行定量的敏感性分析，同样模型参数为25个，生成1 508 组参数样本，得到敏感性分析结果（图6）。与Morris 法的结果相比，蒸发、雨水下渗、地表径流量［图6（a）、图6（b）、图6（c）］均对生物滞留池导水率（B3）最为敏感。而其他参数对蒸发、雨水下渗、地表径流量的响应较小。对峰值流量［图6（d）］而言，Sobol 法中最敏感的参数是生物滞留池导水率（B3），Morris 法中最敏感的参数为生物滞留池植物覆盖率（B1），两者的分析结果不同。这可能由于Morris 法的采样次数较少，或者Sobol 法考虑参数之间的相互作用影响较大，引起两者分析结果之间的差异，这种差异原因在其他文献中也有所讨论［22］。但是从Sobol定量分析的结果来看，B1和B3对峰值流量影响均较大。Sobol 法的计算可作为Morris 法的一种补充与印证。

图6 Sobol法敏感性分析结果Fig.6 Sensitivity analysis results of the Sobol method

2.3 EFAST法分析结果

为了与Sobol 法进行定量比较，本研究同时采用EFAST 法进行敏感性分析。样本数量为2 150组，得到不同LID设施参数的敏感性分析结果（图7）。在EFAST 法结果分析中，蒸发［图7（a）］，最敏感的参数是生物滞留池导水率（B3），植被草沟植物覆盖率（V1）、绿色屋顶田间持水量（G5）以及透水铺装粗糙系数（P2）也比较敏感。雨水下渗［图7（b）］和地表径流量［图7（c）］，最敏感的参数是生物滞留池植物覆盖率（B1），与Morris 法和Sobol 法的分析结果相同。而峰值流量［图7（d）］，最敏感的参数是生物滞留池植物覆盖率（B1），次之是生物滞留池粗糙系数（B2），此结果与Morris 法的结果一致，与Sobol 法的结果不同。造成两种结果差异的原因，一方面由于采样数量的影响，另一方面由于参数间相互耦合造成的影响。

图7 EFAST法敏感性分析结果Fig.7 Sensitivity analysis results of the EFAST method

2.4 EFAST法、Morris法和Sobol法比较

表2比较了3 种全局敏感性分析方法筛选出的LID 设施对输出变量影响最大的4 个参数。从表2可以看出，三者分析的参数敏感性极为相似，但是排序有所不同。原因一是分析方法的样本数不同，Morris法的样本量较小，而两种定量分析法的样本量，计算量均较大。原因二是各输出变量的敏感性分析结果受各参数之间的相互作用的强弱影响，在此方面EFAST 方法优势性更强。与Morris法相比，Sobol法和EFAST法可以进一步的定量分析参数对输出变量的贡献率。EFAST 法的计算更稳健高效，因此在模型参数较多时，首选EFAST 法。而参数少，样本数量少的情况下，首选Morris法进行参数的定性分析。

3 结 论

通过SWMM 模型结合3 种全局敏感性分析方法，从蒸发、雨水下渗、地表径流量及峰值流量4方面综合评估4种LID设施中25个模型参数的敏感性。研究表明，生物滞留池导水率对蒸发量、雨水下渗和地表径流量影响最显著，生物滞留池植物覆

盖率和导水率对峰值流量影响最显著。本研究采用不同全局敏感性分析方法的结果具有一致性，因此证明对LID 设施参数的筛选具有可行性，对LID 设施的配置和海绵城市的优化设计可起到指导性作用。3 种敏感性分析方法中，定性法（Morris）、定量法（Sobol/EFAST）具有不同的优缺点，Morris 计算样本少，计算速度快；Sobol 法和EFAST 法分析精准，但是样本需求量大，计算时间长。多种方法的应用可使敏感性分析更具有可靠性和准确性。