基于VAR模型的城市居民用水需求同水价和收入的动态关系研究

2022-06-25宋宜林陈梓豪

中国农村水利水电 2022年6期

许萍，宋宜林，陈梓豪

（1.北京建筑大学城市雨水系统与水环境教育部重点实验室，北京 100044；2.北京建筑大学水环境国家级实验教学示范中心，北京 100044）

0 引言

随着社会经济的快速发展，我国水资源短缺形势愈发严重，城市用水供需矛盾也日益加剧［1］。通过利用价格杠杆对用水需求进行管理，是缓解水资源供需矛盾的重要手段之一［2］。近年来，居民家庭用水量在我国城市用水结构中占比不断增加，达到全国城市用水总量的39.69%（2019年）［3］，有巨大的节水潜力，因此如何有效利用水价引导居民合理用水是推进节水工作的新思路。水资源与一般的居民消费商品不同，其具有很强的公共产品属性［4］，需要保障居民的基本用水需求，是人民生活的必需品，政府势必需要对水价进行整体调控，防止水价如其他普通消费品一般随市场需求而自由变化。但目前我国普遍使用的平均成本定价法仅以工程成本定价，难以反映水资源的稀缺性，不利于提升居民的节水意识，对减少水资源浪费作用有限［5］。同时，我国现行城市水价中包含的资源水价（水资源费/税）收费标准长期较低，难以发挥其对水资源的节约利用效果［6-8］。

若干实证案例研究表明，水价对用水需求存在一定影响，张家瑞等［9］通过建立流域水价政策复杂系统模型，对滇池流域水价政策进行仿真分析，发现水价上升能够有效降低居民生活用水量；魏强［10］运用系统动力学仿真模拟发现，长春市居民水价由2.5 元/m³提高至4.4 元/m³时，其生活用水总量将下降约0.103 亿m³。但已有研究多集中于对单个城市进行的水价变化与用水需求的分析，而城市间经济水平不平衡导致居民对水价变动的承受程度不同［11-13］，同时，全国各地城市气候不同，而气候变化也在很大程度上决定了居民家庭的生活用水习惯，从而影响居民对水价的敏感程度［14-17］。因此现有研究结果不够全面，缺乏从宏观层面对全国不同类型城市的针对性研究。另一方面，现有研究多是对水价在一段时间内的静态效果进行研究或预测，缺乏水价对用水需求影响的实际动态关系研究，且多是基于双对数模型的价格弹性计算，存在较强的变量内生性问题，难以准确反映二者关系［18］。

因此，本文选取全国8个典型城市（北京、上海、大连、兰州、宁波、长沙、昆明及南宁），通过VAR模型定量表达水价、收入对居民用水需求的影响程度大小，并揭示居民用水需求与水价、收入间的动态关系，旨在为更具针对性的政策出台提供理论依据。

1 研究方法与数据来源

1.1 向量自回归理论

向量自回归模型（Vector Auto Regression models，VAR）是一种时间序列模型，可以有效揭示变量间的动态关系和定量表达变量间影响程度的大小，同时不具有约束性［19］。VAR模型最初由Sims［20］在1980年引入宏观经济分析中，现已被广泛应用于产业结构升级、资源环境污染等因素与经济增长的关系研究，并取得了良好的效果［21-24］。Tian 等［25］分析了GDP 与总用水量之间的动态响应关系，并利用VAR模型对未来水资源利用情况进行预测；Sun 等［26］基于VAR 模型研究了工业废水对经济增长的双向影响机制及其长期动态关系；崔毅［27］基于VAR模型从宏观用水角度说明通过提高生产生活用水占比，对优化地区用水结构的重要作用；王飞等［28］通过VAR模型模拟分析江苏省经济产出、水资源消费和水价间的时变关系，发现适当提高水价对经济发展有促进作用，但对城市总体用水量影响不大。根据国内外研究中对VAR模型应用的经验，该模型适用于用水量与水价及收入等产业产值增长相关指标间的分析。

VAR模型的数学表达式如式（1）所示［29］：

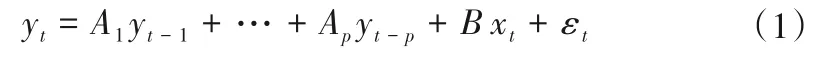
式中：yt是内生变量；xt是外生变量；样本数目为T；A1，A2，…，Ap是待估计的参数矩阵；p是滞后阶数；B是xt待估系数；εt是随机扰动列向量。

VAR模型转化为矩阵表示为：

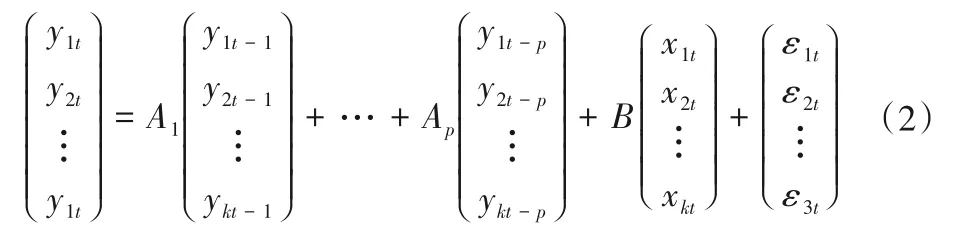
VAR 模型建立的前提要求是各变量应为平稳序列或存在协整关系，方可建立VAR 模型［30］。当模型系统稳定时，即可使用脉冲响应函数和方差分解对冲击进行分析研究［22，23］。

1.2 变量选取与处理

本文主要考察水价（P）及收入（S）对城市居民用水需求的动态影响关系，其中以居民人均年用水量（Q）代表居民用水需求。水价定价与城市水资源丰富度有直接关系，因此以1 000 m³/人划分城市人均水资源量丰富度，对35 个重点城市人均水资源量进行对比，见图1；水费承受能力是水价对用水需求的另一个影响因素［31］，本文以人均可支配收入代表城市居民水费承受能力，35 个重点城市人均可支配收入对比结果，见图2；综合考虑上述两指标并对比水价数据（见图3），选取北京、上海、大连、兰州、宁波、长沙、昆明及南宁8 座具有代表性的城市，分为四组进行对比分析，见表1。其中，人均水资源量选自各省市《水资源公报》，人均可支配收入根据各城市《统计年鉴》确定，水价数据来源于各地方政府或供水服务提供商，样本区间为2005-2019年，因数据可获取行，人均水资源量数据样本时间为2017年。

图1 2017年35个重点城市的人均水资源量对比Fig.1 Comparison of per capita water resources in 35 key cities in 2017

图2 2005-2019年35个重点城市的人均可支配收入对比Fig.2 Comparison of per capita disposable income of 35 key cities from 2005 to 2019

图3 2005-2019年35个重点城市的平均水价对比Fig.3 Comparison of average water prices in 35 key cities from 2005 to 2019

表1 不同类别研究城市Tab.1 Research cities in different categories

考虑到物价变化可能会造成不同年份水价、收入之间的时间差异，故利用商品零售价格指数作为平减指数，将各城市水价与人均居民可支配收入转化为基年不变价格与不变收入。商品零售价格指数来源于各城市的历年《统计年鉴》，并以2005年为基准进行平减。此外，为避免数据的剧烈波动，消除可能存在的异方差，对各项原始数据进行对数化处理，分别计为lnQ、lnP和lnS。本文采用EViews 软件进行模型的检验与构建等系列工作。

2 研究结果与分析

2.1 序列平稳性检验

为避免模型出现伪回归现象，保证结果的可靠性，本文采用ADF 检验法（Augmented Dickey-Fuller Test）对各城市变量序列平稳性进行检验，若序列不平稳，则可对其差分处理，北京市检验结果见表2。

表2 北京市各变量序列平稳性检验结果Tab.2 Test results of sequence stationarity of variables in Beijing

根据表2，北京市lnQ和lnS为平稳变量，而lnP为非平稳的，在对其进行一阶差分处理并再次检验后通过，DlnP为平稳变量。在其他城市的检验中，上海、宁波、长沙和昆明的各变量序列均平稳，大连、兰州和南宁则同样存在不平稳变量序列，需进行差分处理，而在对各不平稳变量进行一阶差分处理后，再次检验显示均通过。

然而使用差分后的数据构建VAR 模型往往会损失总量的长期信息［30］，导致分析结果准确性下降。而随着协整理论的发展，对于非平稳时间序列，只要各变量之间存在协整关系也可以直接利用原变量序列建立VAR模型［32］，故对包含非平稳变量序列的城市进行协整检验，若检验通过，则利用原数据建立VAR模型。

2.2 VAR模型的建立与系统稳定性检验

VAR 模型建立的关键前提为确定滞后阶数，只有确定了滞后阶数，才可确定VAR模型的形式，可按照少数服从多数原则，根据LR、FPE、AIC、SC和HQ五种检验准则的结果进行综合判断后确定滞后阶数。北京市检验结果见表3。

表3 北京市VAR模型的滞后阶数检验Tab.3 Lag order test of VAR model in Beijing

由表3可知，在5 项检验中有3 项的滞后阶数指向1 阶，故北京市VAR 模型的最佳滞后阶数为1 阶，遵循以上过程对其他城市进行检验的结果显示：大连、兰州、宁波、长沙和南宁的最佳滞后阶数均为1阶，上海和昆明则为2阶。

为保证模型稳定有效，采用Johansen 协整检验法对出现非平稳变量现象的城市进行检验。北京市协整检验结果见表4。

表4 北京市VAR模型的协整检验结果Tab.4 Cointegration test results of VAR model in Beijing

表4结果表明，不论是迹检验还是最大特征值检验，其结果均在5%的显著性水平下拒绝无协整关系的原假设，故变量间存在协整关系，可建立VAR 模型。而遵循以上过程，对其他存在非平稳变量序列的城市进行协整检验后，结果也均显示各变量间存在协整关系，检验通过。

稳定的VAR模型是进行脉冲响应分析和方差分解的前提，AR根图检验是确定VAR模型稳定性的主要方式，若AR根均落在单位圆内，则说明VAR模型稳定，反之亦然。北京市AR根图检验结果，见图4。

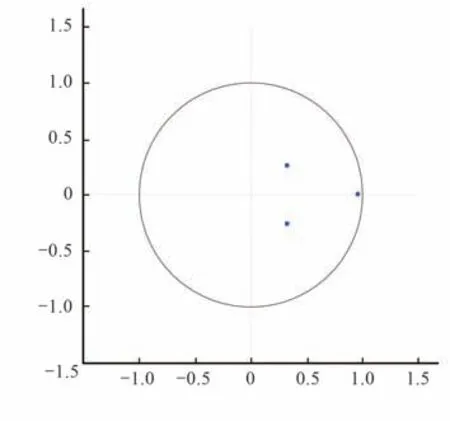
图4 北京AR根图检验结果Fig.4 Test results of AR root diagram in Beijing

根据图4，北京市VAR 模型所有的AR 根均在单位圆内，说明各模型稳定，可利用脉冲响应函数与方差分解展开相应分析。其他各城市VAR模型经检验后所有的AR根也均在单位圆内，检验通过。

2.3 城市居民用水需求变化与水价的动态关系分析

参照基于北京市数据进行的VAR模型的检验与建立过程，其他城市均遵循此过程进行检验，根据城市分组情况对各城市模拟结果进行对比分析。

2.3.1 脉冲响应函数分析

脉冲响应函数用于刻画当VAR 模型系统受到某个内生变量的冲击时，给其他内生变量所带来的影响，并通过脉冲响应图展现出每个变量的动态影响过程及影响的正负。当随机误差项施加一个单位大小的正向标准差的冲击后，若水价对居民用水需求的冲击响应度为负，表明水价对用水需求产生了有效抑制；而若冲击响应度为正，则表明水价对用水需求的抑制失效；收入则反之亦然。

（1）人均水资源量较低-收入水平较高组。在人均水资源量相对较低而收入水平相对较高的情况下，北京水价高于上海，两者水价和收入对居民用水需求的冲击效应有所不同，见图5。

根据图5（a）～（d），水价相对较高的北京市，其lnP对lnQ的冲击在1～10 期内均为负，冲击响应度在第2 期达到最大，后逐渐降低，说明北京市水价对居民用水需求产生了明显的抑制效应，居民用水量下降，但随着时间的推移，水价的抑制强度逐渐降低，其原因可能在于居民对水价的敏感度将随时间减弱；lnS对lnQ的冲击则在1～10 期内均为正，但冲击响应度均不大，说明收入对居民用水需求具有一定的拉动效应，但影响强度低于水价的抑制效应。而水价相对较低的上海市，其lnP对lnQ的冲击在第2 期为负，第3 期接近0，第4～7 期为正，呈现出正负交替形态，说明上海水价虽相对较低，但仍对居民用水需求在前期产生了较为明显的抑制效应，居民用水量有所下降，但抑制效应难以持续，后期居民用水需求出现反弹现象；而lnS对lnQ的冲击则为负向波动，后趋近于0，说明收入同样对居民用水需求产生了一定的抑制，居民用水量有所下降。

图5 分类1典型城市的脉冲响应函数图Fig.5 Impulse response function diagram of typical cities in Category 1

对于上海市出现的水价抑制失效的情况，其原因可能为受物价变化的影响，水价实际上出现了较长时间的连续下降。如上海市于2013年将水价调整水价后6年未再做出调整，加之水价本身较低，导致其2019年的不变价格仅为2.83 元/m³，远低于其3.45元/m³的名义价格。所以，可能出现了因不变价格下降而导致的居民用水量上升的情况。另一方面，可能因为当地居民家庭用水量已达刚性需求，下降空间有限。上海市人均居民家庭用水量在2005年至2010年间已从157.24 L/（人·d）下降至116.63 L/（人·d）的较低水平。继而居民用水量开始逐渐回升，在2019年时达122.83 L/（人·d）的规范水平，故水价表现出前期有效抑制，而在居民用水量达到刚性需求后，表现为失效状态。

（2）人均水资源量较低-收入水平较低组。在人均水资源量相对较低且收入水平也相对较低的情况下，对比分析大连和兰州的水价及收入对居民用水需求的冲击效应，见图6。

根据图6（a）～（d），水价相对较高的大连市，其lnP对lnQ的冲击与北京市相似，在1～10 期内均为负，且冲击在第2 期达到最大，后逐渐降低；相对来说，其lnS对lnQ的冲击则几乎与横轴贴合。说明大连市水价同样对居民用水需求产生了明显的抑制效应，居民用水量有所下降，但随着时间的推移水价的抑制强度逐渐降低；而收入对居民用水需求的影响则相对不明显。而水价较低的兰州市，其lnP对lnQ的冲击在1～10期内均为正，而lnS对lnQ的冲击在1～10 期内均为负，但幅度相对较小。说明兰州市水价未能对居民用水需求产生抑制效应，居民用水量仍会上升；而收入则呈现出微弱的抑制效应。

图6 分类2典型城市的脉冲响应函数图Fig.6 Impulse response function diagram of typical cities in Category 2

大连与兰州同属严重缺水型城市，二者2017年人均水资源量均不足200 m³/人，同时兰州市人均可支配收入反而相对更低，本应对水价更为敏感，但由于兰州居民水价自身长期过低，2005-2019年其居民平均水价仅为2.29元/m³，排在全国35个重点城市中的第31位，因此导致价格信号无法有效传达水资源的紧缺程度，致使水价的抑制效应失效。同时，兰州市水价的不变价格在2005-2019年的15年间有2/3 的年份在下降，所以水价不仅完全失效，还出现了因不变价格下降而导致的居民用水量上升的情况。此外，兰州市2005-2019年居民人均年用水量平均值为129.78 L/（人·d），接近《城市居民生活用水量标准》要求上限，说明并非因居民用水达到刚性需求而致使水价失效。

（3）人均水资源量较高-收入水平较高组。在人均水资源量相对较高且收入水平也相对较高的情况下，水价相对较高的宁波市和水价相对较低的长沙市，两者水价和收入对居民用水需求的冲击效应，见图7。

根据图7（a）～（d），水价相对较高的宁波市与水价相对较低的长沙市，二者lnP对lnQ的冲击均在1～10 期内均为正；而lnS对lnQ的冲击则均为负且幅度较小。说明二者水价均未能对居民用水需求产生抑制效应，呈现出失效状态，居民用水量仍会上升；而收入的增加则将小幅降低居民用水量，呈现出微弱的抑制效应。

图7 分类3典型城市的脉冲响应函数图Fig.7 Impulse response function diagram of typical cities in Category 3

宁波市与长沙市均属于水资源较为丰富且收入水平较高的城市，且宁波市多年居民平均水价为2.92 元/m³，在35 个重点城市中排名第12 位，属于较高水价水平；而长沙市则仅为2.11元/m³，排名第34 位，属于较低水价水平，但两者均表现出水价抑制效应失效。同时，二者2005-2019年居民人均年用水量平均值为222.07 L/（人·d）和270.28 L/（人·d），均高于《城市居民生活用水量标准》要求，均不存在居民用水量达到了刚性需求的现象。故推测即使水价相对较高，但由于城市水资源相对丰富，降低了居民对水资源稀缺性的认知，对水价发挥其抑制效应产生了一定的阻碍。

（4）人均水资源量较高-收入水平较低组。在人均水资源量相对较高而收入水平相对较低的情况下，水价相对较高的昆明市和水价相对较低的南宁市，两者水价和收入对居民用水需求的冲击效应，见图8。

图8 分类4典型城市的脉冲响应函数图Fig.8 Impulse response function diagram of typical cities in Category 4

根据图8（a）～（d），水价相对较高的昆明市，其lnP对lnQ的冲击在第2 期为负，但在第3 期几乎为0，第4 期为负，后逐渐波动趋近于0，说明昆明市水价对居民用水需求产生了一定的抑制效应，居民用水量有所下降，但随着时间的推移水价的抑制强度逐渐波动降低；而lnS对lnQ的冲击则在第2期为负，第3期为正，总体呈现出不规则正负交替形态，最终趋近于0，说明收入对居民用水需求的影响则由抑制与促进交替变化。而水价相对较低的南宁市，其lnP与lnS对lnQ的冲击均在1～10期内为正。说明南宁市水价未能对居民用水需求产生抑制效应，呈现出失效状态，居民用水量仍会上升；而收入的增加同样使得居民用水量有所上升。

值得注意的是，虽然昆明市水资源量相对较为丰富，但与其他同类城市相比，其水价依旧能呈现出一定的抑制效应，其原因可能为：①虽其2017年人均水资源量可达到1 134.00 m³/人，水资源量较为丰富，但由于滇池污染严重，无法达到饮用标准，因而实际面临着严重的水质型缺水问题［33］，居民具有相对较强的水危机感，2005-2019年昆明居民人均用水量平均值可达到107.88 L/（人·d），处于规范对其要求中的较低水平。②昆明水价一直处于较高水平，2005-2019年平均水价可达3.21 元/m³，可排在35 个重点城市的第7 位。所以，表明水资源量丰富的城市其水价的抑制效应并不是绝对无效，且可印证居民对水资源紧缺的认识程度或将影响水价的抑制作用。

2.3.2 方差分解

根据方差分解原理，利用方差分解进行水价和收入对居民用水需求的影响贡献度分析，结果见表5、6。

根据表5，在人均水资源量较低的情况下，典型城市水价对居民用水需求的方差分解的平均贡献度集中在12.14%～26.41%，远高于收入的0.10%～1.16%，表明水价对改变居民用水需求的程度远高于收入。此外，各城市水价与收入合计的平均贡献度均不超过30%，表明至少有70%的居民用水需求变化由其他因素导致。

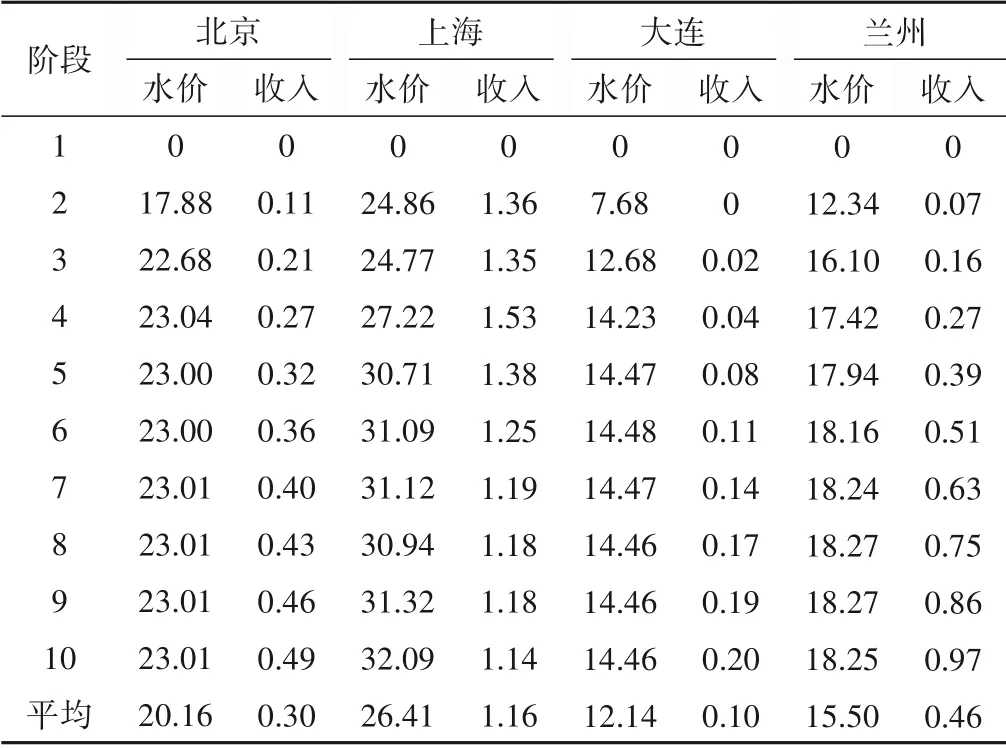
表5 人均水资源量较低的典型城市组方差分解的贡献度结果 %Tab.5 Contribution degree results of variance decomposition of typical urban groups with low per capita water resources

根据表6，在人均水资源量较高的情况下，典型城市水价对居民用水需求的方差分解的平均贡献度集中在2.72%～10.10%，虽同样高于其收入平均贡献度，但远低于人均水资源量较低的典型城市结果，表明在人均水资源量较低的城市，其水价对改变居民用水需求的程度远高于人均水资源量较高的城市，与一般认知相符。

表6 人均水资源量较高的典型城市组方差分解的贡献度结果 %Tab.6 Contribution degree results of variance decomposition oftypical urban groups with high per capita water resources

目前多数研究认为水价对用水需求的影响小于收入［34-36］，而本文结果则与之相反，其原因可能在于：①已有研究的时间较早，而在与本文研究时间就近的研究中出现了结果接近的情况，如张立尖等［11］对上海市价格弹性的计算研究（时间跨度2005-2015年）中同样得出价格弹性的绝对值（-0.160±0.016）大于收入弹性（0.015±0.011）；②已有研究多采用双对数模型为计算方法，而该方法存在一定的内生性问题，导致结果有所差异，郑新业等［18］采用联立方程式法解决内生性问题后计算出我国水价的价格弹性（-2.43）的绝对值同样大于收入弹性（1.30），而本文结果由于采用VAR 模型得出，同样避免了内生性问题，因而得出的结果相似。