基于精英族系遗传算法的AUV集群路径规划
2022-06-25冯豪博赵振轶
冯豪博, 胡 桥, 赵振轶
(1. 西安交通大学机械工程学院, 陕西 西安 710049;2. 陕西省智能机器人重点实验室, 陕西 西安 710049)
0 引 言
随着无人化技术的迅猛发展,水下无人集群系统的军用和民用价值日益凸显。自主式水下航行器(autonomous underwater vehicle, AUV)因其作业范围广、安全性高、功能性强等特点,逐渐发展成为应用最为广泛的水下无人设备。由于AUV集群对协同控制能力的高需求,路径规划系统成为了AUV集群智能系统必不可少的重要组成部分,长期以来一直受到国内外学者的广泛关注。
多智能体路径规划(multi-agent path planning,MAPP)问题是一类寻找多个智能体从起始位置到目标位置且无冲突的最优路径集合问题。MAPP被广泛应用于情报侦察、目标监视、集群作战等领域,而与单智能体路径规划相比,多智能体系统的航行控制更为复杂。对于AUV集群而言,在航行过程中不仅需要考虑岛屿、暗礁、船舶等复杂环境的影响,还需要对AUV间航路规划进行统筹协调,因此AUV集群航行控制系统需要具备规划多条无冲突的可行路径的能力。
在无人集群的单路径规划方面,国内外学者的大量研究已经取得了各种各样的成果。Sang等针对人工势场法容易陷入局部的问题,通过A算法进行全局路径规划获得子目标序列,再使用子目标人工势场法实现水面无人艇舰队的航路规划。王乐乐等针对多机器人在形成编队队形情形下的路径规划问题,建立搜索树扩展方向与队形方向之间的联系,将快速搜索树算法应用到集群编队路径规划中。Lima等针对无人集群在三角形队形情况下的路径规划问题,提出一种新的路径规划数学建模方法,并基于粒子群优化、差分进化等算法的仿真验证了该数学模型的可行性。
AUV集群沿着单路径航行时,通常以形成多机编队的方式行进,对环境的障碍分布情况、可行空间大小有着很高的要求。在AUV集群向目标点行进的过程中,编队规模越大,在维持队形的情况下所需的路径宽度也越大。在以单机行进方式航行的情况下,AUV集群沿着不同路径行进能更加充分利用环境空间,相比于单路径行进,其总耗时(第一台AUV出发时间与最后一台AUV到达时间的间隔)更短。而在以多AUV编队行进的情况下,环境空间障碍密集程度对编队规模起到了限制作用,根据AUV集群规模选择合适的编队规模和路径数量将有利于规划所需路径、缩短行进耗时。因此,多路径规划在实现AUV集群航行路径规划过程中起到重要作用。
相比于无人集群的单路径规划,国内外学者对于基于多路径的MAPP研究则相对较少。李征等针对传统路径规划算法难以满足多无人机协同飞行需求的问题,通过最优控制建模将多无人机路径规划问题转化为非线性优化问题,提出一种基于Radau伪谱法的无人机集群路径规划方法,但此方法主要基于数值求解方式,可扩展性较低。Babel针对无人集群同时或顺序到达目标点的航迹规划问题,提出一种基于同时到达原则的无人集群路径规划方法,但该方法所产生的路径存在交叉现象且并不能实现时间最优的目的。丁佳宇等采取人工势场法,将已规划路径点作为障碍点,对无人机依次规划路径实现无人机集群的路径规划,但该方法不能对各路径间关系进行协调优化,随着无人机集群规模的增大,所规划的路径长度将显著增长。
本文针对多路径规划问题,以路径长度为评价指标,通过将基因适应度项加人适应度评价函数,并通过隐性基因调节路径宽度,提出了精英族系遗传算法(elite family genetic algorithm, EFGA)。同时,在EFGA的基础上,本文针对AUV集群路径规划问题,提出了一种MAPP方法。仿真结论表明,所提方法能够通过求解无冲突路径集合实现AUV集群的多路径规划,减少AUV集群的航行时间。
1 环境模型
环境建模起着将环境信息抽象为易于计算机处理的数据信息的作用,对后续的路径规划尤为重要。常用的环境建模方法有栅格法、可视图法、拓扑法等。为简化问题的分析和求解,本文将三维水下空间简化为二维。由于AUV编队规模的大小会根据不同的需求发生变化,因此本文选择使用具有栅格粒度可调特点的栅格空间建模。
1.1 栅格空间建模
栅格法的原理是将整个空间按照一定的粒度拆分成一个个连续但不交叉的栅格,每一块栅格的状态由其所处位置的环境信息决定。模型如图1所示,将正方形空间平均分为10×10的格栅网格,其中白色栅格表示可达空间,黑色栅格表示不可达空间。由于出发区域和终点区域的大小对路径规划结果的影响较小,因此忽略出发区域和终点区域大小的影响,起点用黄色栅格表示,终点用蓝色栅格表示。
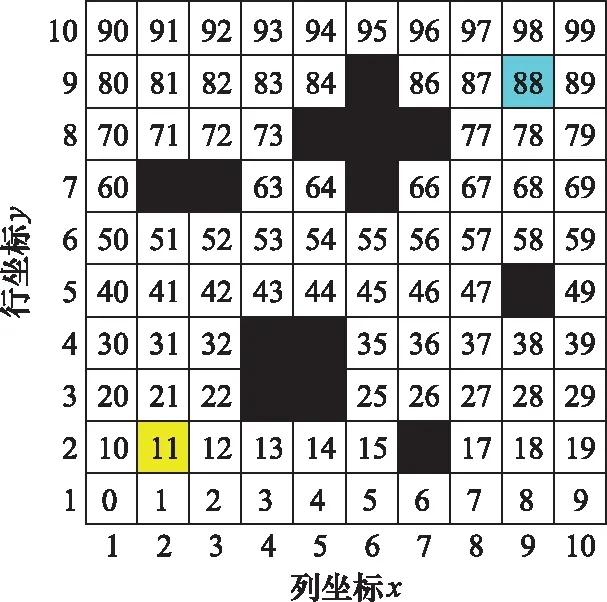
图1 栅格空间建模Fig.1 Environment modeling in grid space
通过序号和坐标(,)共同对栅格空间进行描述。栅格序号以一定的纵横规律对每一块栅格进行编号,栅格坐标与栅格所在行列相互对应。栅格坐标与序号转换关系如下:
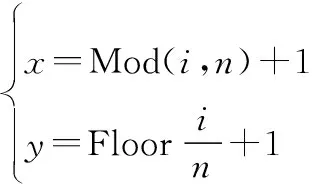
(1)
式中:为栅格序号;为栅格所在列数;为栅格所在行数;为栅格空间总列数;Mod(·)为取余操作;Floor(·)为向下取整操作。
1.2 栅格粒度划分原则
栅格粒度是指栅格空间中每个栅格的尺寸大小。栅格粒度的划分对模型精度、路径规划求解难度有着重要影响。栅格法粒度可调的特点使其适用范围广,但存在时空开销和求解精度存在冲突的问题。过大的划分粒度会导致环境信息的大量丢失,无法对环境空间进行充分的描述,导致路径规划结果与预期不符。而过小的划分粒度则会使路径规划算法所需内存空间和算力资源大为增加,造成不必要的计算机资源浪费,且AUV集群的运动控制性能也制约着过于精确的路径的准确执行。
在进行栅格空间建模时,通常采取将障碍边界扩大而使AUV或AUV编队等效为质点的简化方式,但这种方式会使AUV间避碰约束信息丢失,导致需要对AUV间距离关系进行额外约束,并且这种简化方式会导致空间建模精度随着AUV或AUV编队尺寸的增大而降低,降低路径规划求解结果的精度。
为解决AUV间避碰约束信息丢失的问题,实现对AUV与环境、AUV间位置关系的有效描述,提升栅格空间建模精度,根据对不同求解精度的需求,本文提出了两种栅格粒度划分原则。
1.2.1 基于编队规模的粒度划分原则
在AUV集群在简单环境中以编队方式行进的情况中,路径求解精度易于得到保证,为减小算法求解开销,采用基于编队规模的粒度划分原则。
如图2所示,以三角形编队为例,AUV与障碍间安全距离为,AUV间安全距离为,图示三角形编队规模尺寸则为2+2。在这种情况下,选取编队规模尺寸为栅格粒度。对于AUV以独立行进方式在简单环境中航行的情况下,类似地可以将2作为栅格粒度进行栅格空间建模。

图2 基于编队规模的粒度划分Fig.2 Grid division according to formation size
1.2.2 基于相对复杂系数的粒度划分原则
对于较为复杂的环境,为保证求解精度,采用基于相对复杂系数的粒度划分原则。相对复杂系数是环境复杂度与编队规模尺寸或AUV尺寸之间的度量。环境障碍尺寸越小,编队规模尺寸或AUV尺寸越大,则相对复杂系数越大。
如图3所示,以三角形编队为例,AUV与障碍间安全距离为,AUV间安全距离为l,则图示三角形编队规模尺寸=2+2。

图3 基于环境复杂系数的粒度划分Fig.3 Grid division based on environment complexity coefficient
在这种情况下,栅格粒度选取如下:
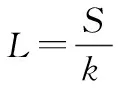
(2)
式中:为相对复杂系数,∈{|=2+1,∈}。一般取值与编队的行列数量相关,但当环境过于复杂时,也可选取较大的值。当=1时,与基于编队规模的粒度划分的结果相同。
2 EFGA
遗传算法最初由文献[23]于1976年提出,是一种通过模拟自然进化过程搜索最优解的方法,被国内外学者广泛应用于求解路径规划问题。但标准遗传算法的核心思想仅对个体与环境之间的关系进行考虑,适应度函数完全由环境因素所决定,以获得适应度最高的单一个体为优化目的,并不适用于求解MAPP问题。
为了更好地求解MAPP问题,本文在标准遗传算法的基础上,选取合适的遗传算子,将基因适应度项加入适应度评价函数中,同时对个体与环境之间的关系、个体间的相互竞争关系进行考量,应用精英族系策略,将优化目标由最优路径转化为无冲突的最优路径集合,并通过隐性基因实现对路径宽度的调节,提出了适用于多路径规划的EFGA算法。
2.1 显性基因和隐性基因
为了满足不同AUV编队规模对可调路径宽度的需求,本节对显性基因和隐性基因进行定义。如图4所示,在以相对复杂系数作为粒度划分原则且=3的栅格空间中,红色实线表示所划分的路径,黄色栅格为显性基因,绿色栅格为隐性基因,即显性基因对应为路径所经过的所有栅格,隐性基因对应为集群编队沿着路径行进所经过的除显性基因以外的所有相邻栅格。
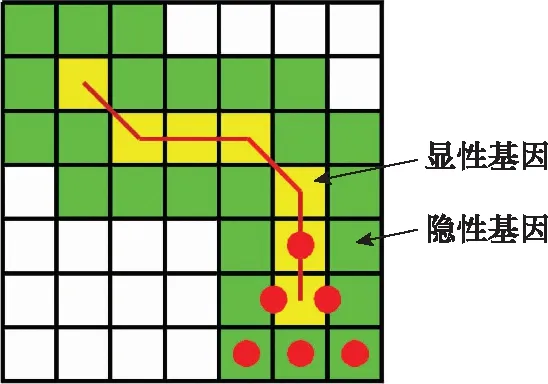
图4 显性基因与隐性基因Fig.4 Dominant gene and recessive genes
若已知显性基因栅格坐标集合为,则隐性基因栅格坐标集合计算如下:
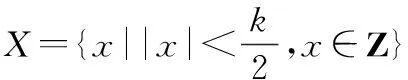
(3)
在以编队规模为原则进行栅格空间建模的情况下,个体只含有显性基因不含有隐性基因,=∅。
2.2 基因编码方式
个体的基因序列由其显性基因采用栅格序号编码形成,如图5所示。

图5 基因序列
Fig.5 Gene sequence
个体的基因序列可用集合表示为={,,,…,}。
为使每个基因序列代表着一条连通路径,对其进行以下约束:
(1) 对∀≠且,∈[1,],有≠;
(2) 对∀∈[1,],∈,其中为所有可达栅格的栅格序号集合;
(3) 对∀∈[1,-1],,+1对应的栅格需相互接触,包括边接触和顶点接触;
(4) 对∀∈[1,-1],,+1形成的路径不能斜穿不可达栅格,如图6所示。
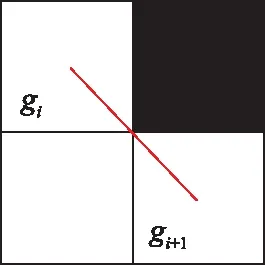
图6 斜穿不可达栅格Fig.6 Passing through unreachable grid obliquely
2.3 遗传算子
为更好地保持种群个体多样性和维持种群个体数量,采用复制、淘汰、变异和交叉4个遗传算子。
231 复制算子
采用三元锦标赛选择法。种群中每个个体均有相同的概率发起复制锦标赛。在发起锦标赛的个体和在种群中随机选取的两个个体中,适应度最大的个体将复制产生一个新个体加入到种群中。个体发起复制锦标赛的概率计算如下:
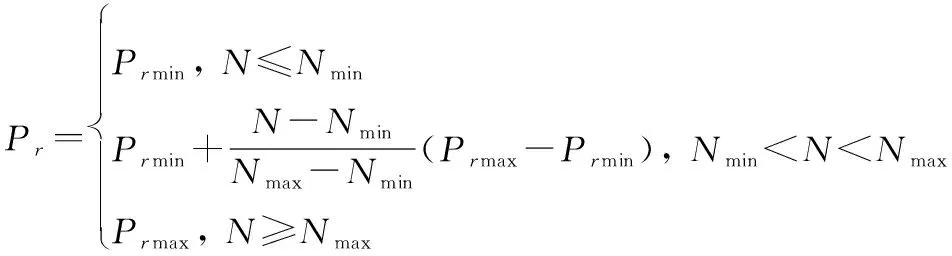
(4)
式中:为当前种群个体数量;[,]为期望种群个体数量范围;min为最小复制概率;max为最大复制概率
232 淘汰算子
采用三元锦标赛选择法。种群中每个个体均有相同的概率发起淘汰锦标赛。在发起锦标赛的个体和在种群中随机选取的两个个体中,其中适应度最小的个体将被从种群中剔除。个体发起淘汰锦标赛的概率计算如下:
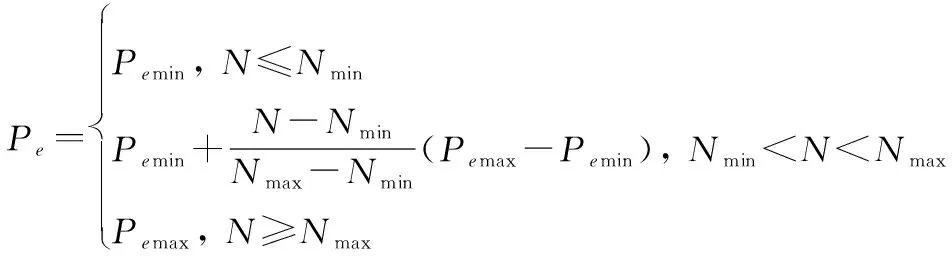
(5)
式中:min为最小淘汰概率;max为最大淘汰概率。
233 变异算子
为保持种群搜索全局空间的能力,采用如下变异算子,其过程如图7所示。种群中每个个体均有相等的变异概率,发生变异的个体会从基因序列中随机位置删除一段随机长度的基因段(首位和末位除外),并在基因序列两断点处相应的栅格所形成的矩形空间范围内随机产生一个新基因,并通过增加基因使其满足上文所述约束条件,形成新的连通路径。
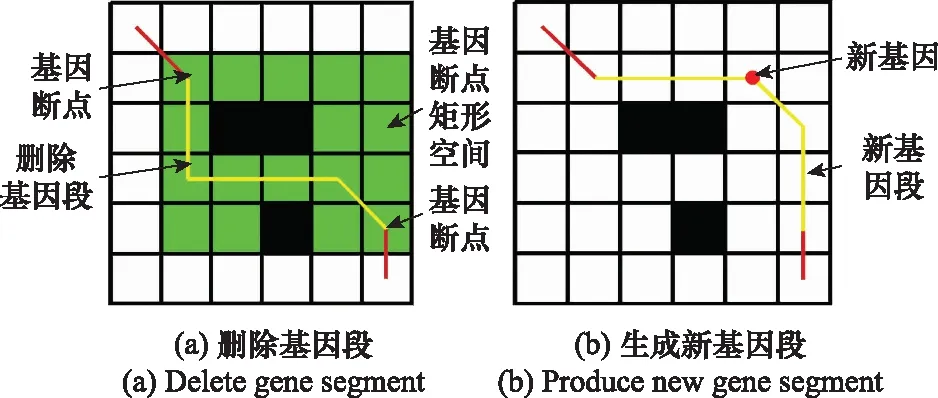
图7 变异算子Fig.7 Mutation operation
234 交叉算子
为进一步提高种群多样性,交叉算子采用单点交叉法和三元锦标赛法。种群中每个个体被选为父个体的概率相同。在每次选取父个体后,从种群中随机选取3个与父个体具有至少一个相同基因(基因序列首位和末位除外)的母个体,其中与父个体适应度差值最大的母个体将与父个体进行单点交叉变异操作。
2.4 精英个体与精英族系
为了实现多路径规划,本文在基因相似度的基础上,提出了精英个体与精英族系的概念。
241 基因相似度
基因相似度是对两个个体的显性基因和隐性基因中相同基因所占比重的度量。个体对个体的基因相似度为个体和个体相同基因数量与个体基因数量的比值。个体对个体的显性基因相似度, ,和隐性基因相似度, ,计算如下:

(6)
式中:,,,分别为个体和的显性基因集合和隐性基因集合;Length(·)为求集合元素个数操作。
242 精英个体
在种群进化过程中,若种群最优适应度值在连续代内不发生变化,则认为在当前竞争环境中种群已经进化出了一个精英个体,精英个体所对应的路径至少可以认为是陷入某一局部最优的求解结果。若越大,精英个体为局部最优解的可能性越低,但进化出所需数量的精英个体所需迭代次数也越多。若越小,种群则可能来不及进化出基因相似度较低的新的精英个体。因此,的选取需要平衡精英个体数量、路径解的质量和基因相似度三者间的关系。
243 精英族系
对于精英个体和个体,若其基因相似度满足一定精英族系判别条件(如, ,>,其中为[0,1]区间内某一恒定值),则认为个体属于所在精英族系。
精英族系判别条件的引入,可以实现对精英个体进行族系划分。精英族系判别条件约宽松(取值越小),属于不同精英族系的精英个体所对应的路径的重合度则越小。因此,通过精英族系判别条件的选取,可以对精英个体所对应的路径重合度进行调节。
2.5 适应度函数
传统路径规划的目标是进化出一个适应度最优的个体,其基于路径长度的适应度函数反应了个体对环境的适应能力。但对于多路径规划问题,所期望的是在有限的环境中进化出适应度总和尽量高的多个个体,因此个体间也存在相互竞争的关系。为对路径间的重合度进行评价,本文提出了基因适应度的概念。
采用基因竞争强度作为不同个体占据同一栅格时相互竞争关系强度的度量。对于精英个体,其所产生的显性基因竞争强度和隐性基因竞争强度计算如下:
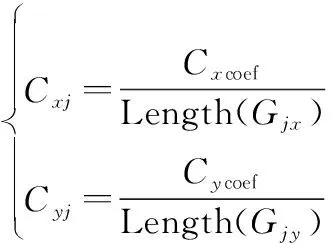
(7)
式中:coef和coef分别为显性基因竞争强度系数和隐性基因竞争强度系数。
对于∀∈,的种群显性基因竞争强度()和种群隐性基因竞争强度()分别计算如下:

(9)
式中:为显性基因中包含的精英个体集合;为隐性基因中包含的精英个体集合;ST为起点栅格序号和终点栅格序号的集合。
个体的基因适应度如下:

(10)
式中:和分别为显性基因适应度系数和显性基因适应度系数。
综合考虑路径长度和路径重合度,本文所用适应度函数如下:
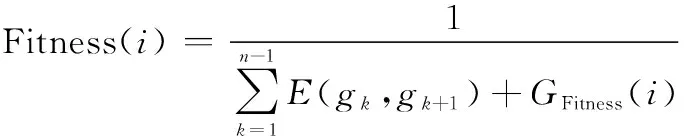
(11)
式中:(,+1)为和+1间的欧几里得距离;为个体的基因序列长度。
2.6 精英选择策略
精英个体的筛选过程就是对路径的筛选过程,精英个体的选择应遵循以下原则:
(1) 同一精英族系中只能含有一个精英个体;
(2) 在精英个体数达到上限后,新的精英个体在满足使所有精英个体适应度总和增大的情况下,会取代原有精英个体。
基于以上原则,根据新的精英个体elite更新原精英个体集合的伪代码如算法1所示。

算法 1 精英选择策略输入 精英个体elite,精英个体集合E输出 精英个体集合E1 初始化:最大精英个体数EliteUpLimit,精英族系判别条件Ss2 IsNewFamily=13 For ∀e∈E do4 Sx,elite,e=GeneticSimility(elite, e)5 If Sx,elite,e>Ss do6 IsNewFamily=07 relativeelite=e8 break9 If IsNewFamily=1 and Length(E)
2.7 EFGA伪代码
EFGA的伪代码如算法2所示。

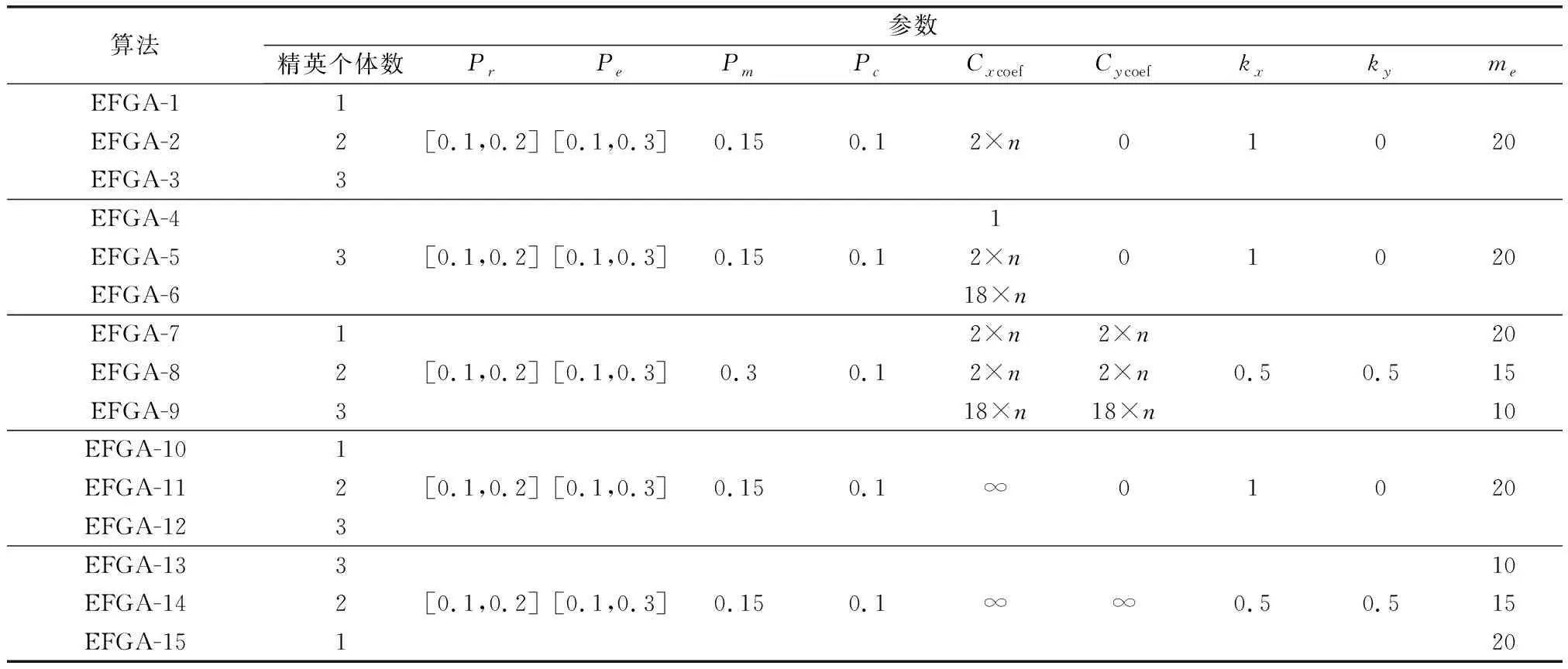
算法 2 EFGA输入 所需路径数K,栅格空间Map输出 精英个体集合E1 初始化:复制概率Pe,淘汰概率Pr,变异概率Pm,交叉概率Pc,个体集合P,个体数N2 P←InitializePopulation(Map)3 E=⌀4 For i=1 to i=N do5 Pr←ReplicationProbability(P)6 Pe←EliminationProbability(P)7 For ∀individual∈P do8 findividual←Fitness(individual)9 If max(findividual)>maxFitness do10 maxFitness,elite=max(findividual)11 k=012 Else do13 k=k+114 If k>K do15 E←EliteSelectionStrategy(E, elite)16 GeneFitnessUpdate()17 For ∀individual∈P do18 If random() 以航行耗时最短为目标的无人集群路径规划是指在满足智能体与障碍、智能体与智能体间均不发生碰撞的条件下,以无人集群从起始位置到终点位置的航行耗时作为评价参数的路径规划问题。 针对此类路径规划问题,本文在上述EFGA的基础上,引入当量路径长度的概念,提出了一种MAPP方法。 当量路径长度是对智能体或智能体编队的出发等待时间和沿着路径从起点到终点所需走过的路径长度的一种度量。由于沿着同一路径航行的智能体或智能体编队需保持一定的安全距离,因此智能体或智能体编队只能在保持安全距离的前提下依次出发沿着路径航行,这就导致后出发的智能体或智能体编队需要等待一定时间。对于路径Path,若规模为×的水下无人集群形成队规模为的编队依次沿着该路径行进,编队间的安全距离为,则当量路径长度计算如下: =+(-1) (12) 式中:为路径Path的实际长度;(-1)是对第个编队的出发等待时间的评价项。 当AUV集群沿着多条路径航行时,路径规划结果应使路径集合中的最大当量路径长度尽量小。当集群规模、航行速度均相同时,编队规模越大,AUV集群的航行时间相对越短,但对路径的宽度要求也越高。 针对个智能体和条路径的MAPP问题,基于EFGA和当量路径长度设计MAPP方法伪代码如算法3所示。 算法 3 MAPP输入 所需路径数K,栅格空间Map,智能体集合AGENT输出 智能体路径集合PATHAGENT1 初始化:智能体间安全距离safedistance2 PATH←EFGA(K, Map)3 For ∀path∈PATH do4 PATHAGENT(path)=⌀5 Le(path)=L(path)6 For ∀agent∈AGENT do7 path=min(Le)8 PATHAGENT(path)←PATHAGENT(path)+a-gent9 Le(path)=Le(path)+safedistance10Return PATHAGENT 为了验证EFGA求解多路径问题和AUV集群路径规划问题的可行性、算法性能以及参数设定对求解结果的影响,在Matlab R2016b中进行了相关仿真,硬件系统环境为i5-10400 @ 2.90Ghz,16.0 GB RAM,操作系统版本为Windows10 19041.746。 EFGA参数设定为初代种群个体数30,期望种群个体数范围[100,200],最大进化代数500,精英族系判别条件max(, ,,,, ,, ,,, ,)>05,其余参数如表1所示。其中,取栅格空间总行数和总列数中的最大值。 表1 EFGA参数 为验证EFGA在简单环境中求解多路径问题的可行性,在图8所示的20×20栅格空间中,起点为(2,2),终点为(19,19),利用表1中EFGA-2和EFGA-3算法对所需路径分别为2和3的多路径规划问题进行求解,并用EFGA-1进行单路径规划作为对比。在分别进行100次仿真后,取典型理想解和典型不理想解如图8所示,统计数据如表2所示。 图8 简单环境下多路径规划典型求解结果Fig.8 Typical results of multi-path planning in simple environment 表2 EFGA-1~EFGA-3的仿真统计数据 由图8(a)~图8(c)可见,EFGA同时具备规划单路径和多路径的能力,精英族系判别条件和基因适应度的引入使各路径间能保持较低的重合度,使可达空间得到充分有效的利用。但图8(d)中的求解结果表明算法所规划的多路径可能会存在“交叉”现象,后续可通过引入交叉惩罚函数来降低此现象发生的可能性。 在表2中:平均收敛代数为所有精英个体已收敛时代数的平均值;平均收敛耗时为所有精英个体已收敛时算法运行时间的平均值;平均路径重合度为每条路径的重合长度之和与所有路径的总长度之比。由表2分析可知,随着所需路径的增多,算法平均收敛耗时近似成比例增加,但平均路径长度无明显增长,平均路径重合度虽有所增大但仍维持在很低水平。上述分析表明,针对简单环境中的多路径规划问题,EFGA能稳定地规划出重合度很低、路径长度相近的多条路径。 由于过大的竞争强度系数通常会导致种群个体多样性的急剧锐减而出现过早收敛的情况,因此可以采用逐步增大竞争强度系数的方法在维持种群个体多样性基础上逐渐降低路径重合度。为验证竞争强度系数对路径重合度的调节能力,利用表1中EFGA-4~EFGA-6算法在图8栅格空间中对路径规划问题进行求解。分别进行100次仿真后,统计数据如表3所示。 表3 EFGA-4~EFGA-6的仿真统计数据 分析表3中数据可知,在其余参数相同的情况下,随着竞争强度系数的增大,路径重合度呈现减小趋势,平均路径长度呈现缓慢增长的趋势,但路径长度变化仍在可接受范围内。 以上分析表明,针对简单环境中的多路径规划问题,可以通过选取合适的竞争强度系数实现对路径重合度的有效调节。 为验证EFGA在复杂环境中规划路径的能力,在图9所示相对复杂系数=3的50×50栅格空间中,起点为(3,3),终点为(38,38),利用表1中EFGA-7~EFGA-9算法对所需路径分别为1~3的路径规划问题进行求解。分别进行100次仿真后,取典型理想解和典型不理想解如图9所示,统计数据如表4所示。 图9 复杂环境下多路径规划典型求解结果Fig.9 Typical results of multi-path planning in complex environment 表4 EFGA-7~EFGA-9的仿真统计数据 由图9(a)可见,EFGA具备规划具有一定宽度的路径的能力。图9(b)和图9(c)表明,即使在环境可行空间非常有限的情况下,EFGA也可以求解出重合度较低的多路径解。但图9(d)中的路径规划结果表明,随着路径数量的增多,有限的可行空间可能会导致在某些狭隘处路径间出现大范围重合或“交叉”现象。 在表4中,平均路径重合度为通过分析表4统计数据可知,随着所需路径的增多,算法平均收敛耗时显著增加,平均路径重合度也有明显增长,但平均路径长度增幅仍维持在较低水平。由表2和表4数据可知,相比于简单环境路径规划问题,由于隐性基因造成的算法空间复杂度增大,算法求解复杂环境中路径规划问题所需时间显著增加,路径重合度也有明显增大。 为了验证MAPP方法求解不同情形下AUV集群路径规划问题的可行性,并与传统单路径规划方法进行对比验证该方法在减少AUV集群航行时间上的有效性,在图10所示20 m×20 m环境空间中分别进行独立航行方式对比仿真和编队航行方式对比仿真,其中黑色区域为障碍,黄色区域为起点,蓝色区域为终点。 图10 环境空间Fig.10 Environment space 4.4.1 独立航行方式 为了比较采用MAPP方法和传统单路径规划方法时AUV集群的航行总耗时,对图10所示环境空间基于相对复杂系数的粒度划分原则进行栅格粒度为1 m的栅格空间建模,利用表1中EFGA-10~EFGA-12算法对所需路径分别为1~3的路径规划问题进行求解,并基于路径互不重合的求解结果用上述MAPP方法进行AUV集群航行模拟,AUV集群规模取10,编队规模取1,AUV航行速度取1 m/s,AUV间安全距离取1 m。在分别进行100次仿真后,取典型路径规划结果如图11所示,统计数据如表5所示。 图11 独立航行方式情况下AUV集群路径规划典型求解结果Fig.11 Typical results of AUV swarm path planning based on independent navigation type 表5 基于EFGA-10~EFGA-12的AUV集群路径规划结果统计数据 在表5中,平均当量路径长度为EFGA路径规划完成后的平均当量路径长度;平均行进耗时为第一台AUV出发时间与最后一台AUV到达时间的间隔。通过分析表5统计数据可知,AUV集群沿着2条路径行进和3条路径行进的行进耗时比沿着单路径行进的行进耗时分别减少了11.8%和15.2%。随着路径的增多,增加路径数所带来的行进耗时减幅逐渐减小,而EFGA规划互不重合的路径集合所需时间却显著增加,因此通常需要综合考虑栅格空间大小、集群规模和计算资源等因素选取合适的路径数。 上述分析表明,本文所提出的MAPP方法可以在基因适应度的基础上利用EFGA不断搜索当前竞争环境下的最优个体,得到无冲突的最优路径集合,并在保证AUV与障碍、AUV间均不发生碰撞的条件下,为每台AUV规划路径长度最优的航行路径,解决了标准遗传算法、A算法等单路径规划方法无法充分利用可行空间规划多条路径的问题,达到缩短AUV集群的航行时间的目的。 4.4.2 编队航行方式 为了进一步验证MAPP方法解决AUV在形成不同规模的编队队形时的路径规划问题的可行性,在图10所示环境空间中基于相对复杂系数的粒度划分原则分别进行栅格粒度为1 m、0.66 m、1 m的栅格空间建模,并利用表1中EFGA-13~EFGA-15算法分别对无编队、形成三机三角编队、形成六机三角编队的AUV集群进行路径规划,AUV集群规模取12,AUV航行速度取1 m/s,AUV间安全距离取1 m,AUV编队与障碍间安全距离取0.5 m,编队间安全距离取2 m。分别进行100次仿真后,取典型路径规划结果如图12所示,统计数据如表6所示。 图12 AUV编队集群路径规划典型求解结果Fig.12 Typical results of AUV formation swarm path planning 表6 基于EFGA-13~EFGA-15的AUV编队集群路径规划结果 由图12可见,在图12(a)所示无编队情形下,AUV可以通过较为狭隘的区域,在环境可行空间充裕的情况下,规划数量较多的路径可以达到减少AUV集群航行时间的目的。在图12(b)所示形成三机三角编队情形下,AUV编队由于需要保持一定的队形,队形规模限制了AUV不能通过狭隘区域,因此通过EFGA算法的隐性基因实现对路径宽度的调节。同时受环境所限,此时EFGA规划的路径长度有所增大。在图12(c)所示形成六机三角编队情形下,AUV编队队形尺寸进一步增大,AUV编队仅能通过宽阔区域,所需路径宽度也相应增大,此时EFGA规划的最短路径长度进一步增大,且受环境所限,仅存在一条最短路径,此时AUV航行方案只能采取逐个编队依次前行方式。 通过分析表6统计数据可知,无编队情形下AUV集群行进时间最短,这是由于EFGA算法充分利用了环境空间中的狭隘通道求解出3条无碰撞的最优路径,有利于基于当量路径长度规划得到航行时间最短的AUV集群航行方案。在形成三机三角编队情形下,原始路径长度有所增大,相应的AUV集群行进时间有所增加。在形成六机三角编队情形下,AUV集群行进时间最大,这是由于环境中仅存在一条宽度足够的最短路径,AUV编队只能采取逐个编队依次前行的方式,不能充分利用环境空间中的狭隘通道。 上述分析表明,本文提出的MAPP方法不仅能解决常规的无编队AUV集群最优路径规划问题,通过隐性基因对路径宽度进行调节,还可以在保证栅格空间建模精度的情况下,根据实际AUV集群的编队需求,求解不同路径数量和不同路径宽度的AUV编队集群最优路径规划问题,解决了标准遗传算法、A算法等单路径规划方法难以满足AUV编队集群对更为高效的多路径航行方式、与不同集群规模相匹配的可调路径宽度需求的问题,达到提高AUV集群在不同应用情形下求解最优路径规划问题能力的目的。 MAPP是水下无人集群航行控制中至关重要的一环,本文针对AUV集群路径规划问题,提出了EFGA,并在此基础上设计了一种MAPP方法。具体工作如下: (1) 提出了基于编队规模和基于相对复杂系数的两种栅格粒度划分方法,并在此基础上对显性基因和隐性基因进行了定义,通过栅格建模、显性基因和隐性基因实现了对智能体与障碍、智能体间不发生碰撞条件的描述。 (2) 将基因适应度项引入适应度函数,实现对路径长度和路径重合度的综合评价,并在精英个体和精英族系的基础上,针对多路径规划问题提出了精英族系选择策略和EFGA,通过隐性基因实现对路径宽度的调节,同时竞争强度系数的引入可以实现对路径重合度的有效调节。仿真结果表明,该算法具有求解无冲突的路径集合的能力,可以为解决以同时到达为目的的路径规划问题提供参考。 (3) 设计了一种基于EFGA的MAPP方法。该方法根据EFGA求解的无冲突多路径集合,根据当量路径长度将AUV集群合理分配到各个路径上。通过对AUV集群路径规划问题的仿真验证,与单路径规划相比,该方法所得到的路径规划方案的AUV集群航行耗时明显减少,且能根据不同集群规模规划相应宽度的最优路径集合,解决了单路径规划方法不能充分利用环境空间规划多条可行路径的问题和不能满足AUV编队对可调路径宽度需求的问题。 值得指出的是,在竞争强度系数较低的情况下,EFGA所规划的路径存在“交叉”现象,降低了算法的收敛速率,进一步研究可以考虑在适应度函数中引入交叉惩罚项或优化交叉算子以避免此现象的发生。3 MAPP
3.1 当量路径长度
3.2 MAPP方法

4 仿真实验与结果分析
4.1 简单环境下多路径规划
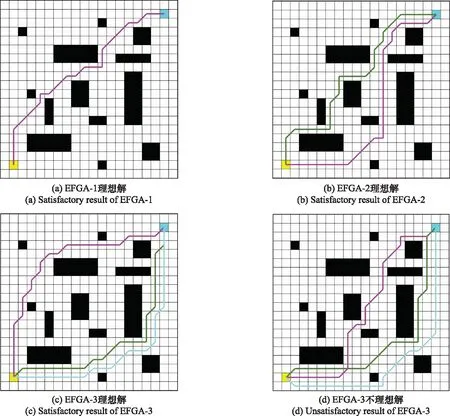
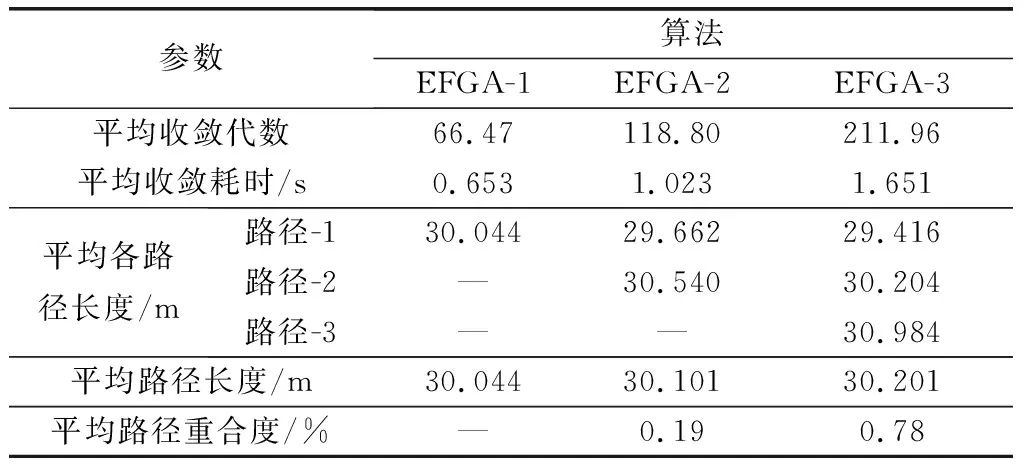
4.2 竞争强度系数对路径重合度的调节能力

4.3 复杂环境下路径规划

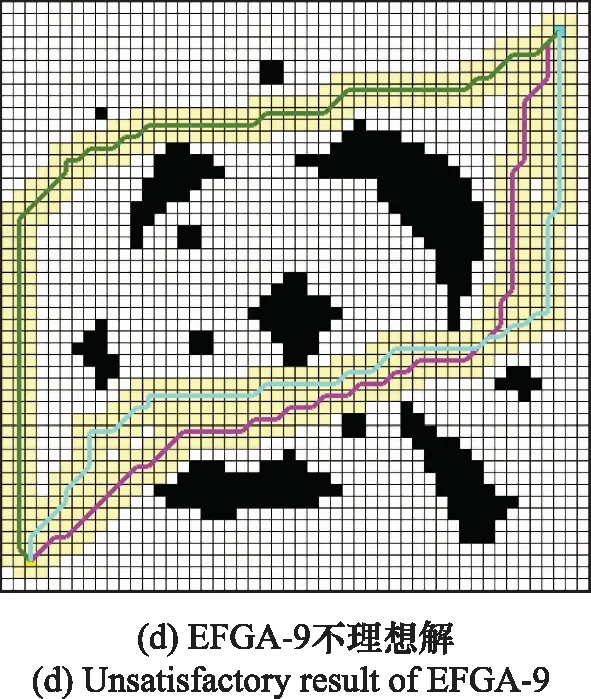

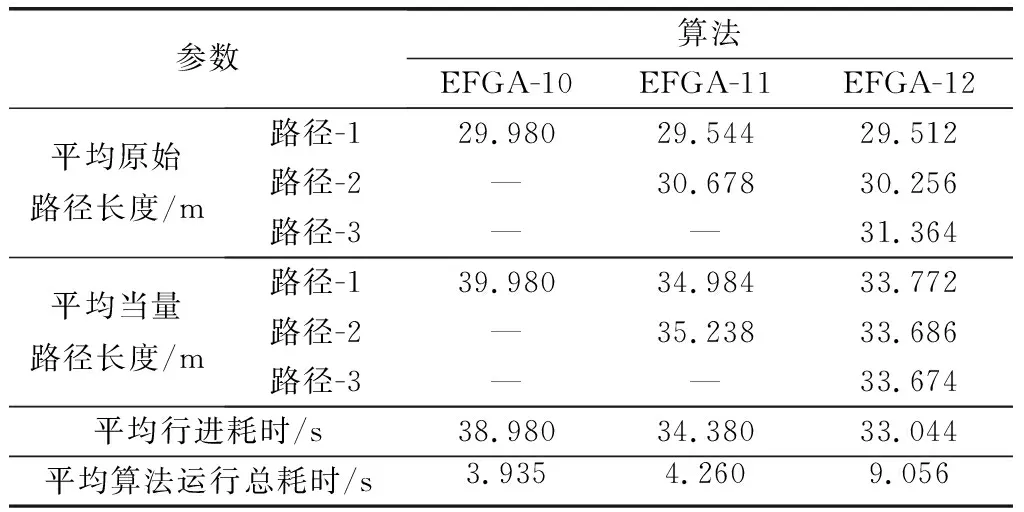
4.4 AUV集群路径规划





5 结 论
